数据结构-线性表的应用
目录
- 前言
- 一、有序表的合并
- 1.1 顺序表实现
- 1.2 单链表实现
- 二、稀疏多项式的相加和相乘
- 2.1 稀疏多项式的相加
- 2.2 稀疏多项式的相乘
- 总结
前言
本篇文章介绍线性表的应用,分别使用顺序表和单链表实现有序表的合并,最后介绍如何使用单链表实现两个稀疏多项式的相加和相乘。
一、有序表的合并
已知线性表La和Lb的数据元素按值非递减有序排列,现要求将La和Lb合并为一个新的线性表Lc,且Lc中的数据元素仍按值非递减有序排序。
非递减指可以有相同的值出现在同一个线性表中
L a = ( a , b , c ) La=(a,b,c) La=(a,b,c)
L b = ( c , d , e , f ) Lb=(c,d,e,f) Lb=(c,d,e,f)
L a La La和 L b Lb Lb合并后
L c = ( a , b , c , c , d , e , f ) Lc=(a,b,c,c,d,e,f) Lc=(a,b,c,c,d,e,f)
1.1 顺序表实现
算法步骤
- 创建一个空表Lc
- 依次从La或Lb中摘取元素值较小的结点插入到Lc表后,直至其中一个表变为空为止
- 继续将La或Lb其中一个表的剩余结点插图到Lc表的最后
代码实现如下
//定义返回值状态码
#define SUCCESS 1
#define ERROR 0//这里假设元素的数据类型为char
typedef char ElemType;//定义一个线性表
struct SeqList {int MAXNUM; //线性表中最大元素的个数int n; //线性表中实际的元素个数,n <= MAXNUMElemType* element; //存放线性表元素,element[0],element[1]...element[n-1]
};//定义一个SeqList的指针类型
typedef struct SeqList* PSeqList;
//合并两个有序表
void mergeList_seq(PSeqList La, PSeqList Lb, PSeqList Lc)
{ElemType* pa = La->element;ElemType* pb = Lb->element; //指针pa和pb分别指向两个表的第一个元素Lc->n = La->n + Lb->n;Lc->MAXNUM = Lc->n;Lc->element = (ElemType*)malloc(sizeof(Lc->n)); //为合并的新表分配一个数组空间if (NULL == Lc->element){printf("malloc fail!\n");exit(ERROR);}ElemType* pc = Lc->element; //指针pc指向Lc表的第一个元素ElemType* pa_last = La->element + (La->n - 1); //指针pa_last指向La表的最后一个元素ElemType* pb_last = Lb->element + (Lb->n - 1); //指针pb_last指向Lb表的最后一个元素while (pa <= pa_last && pb <= pb_last){if (*pa <= *pb)*pc++ = *pa++;else*pc++ = *pb++;}while (pa <= pa_last) *pc++ = *pa++; //Lb表到达表尾,将La表中剩余元素加入Lcwhile (pb <= pb_last) *pc++ = *pb++; //La表到达表尾,将Lb表中剩余元素加入Lc
}
1.2 单链表实现
为了方便使用,选择带头结点的单链表
算法步骤
- pa和pb指针分别指向La和Lb的首元结点
- pc指向La的头结点,用La的头结点作为Lc的头结点
- 依次从La或Lb中摘取元素值较小的结点插入到Lc表后,直至其中一个表变为空为止
- 继续将La或Lb其中一个表的剩余结点插图到Lc表的最后
代码实现如下
//假设数据元素类型为char
typedef char ElemType;//定义结点类型
struct Node;
typedef struct Node* PNode; //假设作为结点指针类型
struct Node {ElemType data; //数据域PNode next; //指针域
};typedef struct Node* LinkList; //假设作为单链表类型//合并两个有序表
//带头结点
void mergeList_link(LinkList* La, LinkList* Lb, LinkList* Lc)
{PNode pa = (*La)->next;PNode pb = (*Lb)->next;PNode pc = *La;*Lc = *La; //用La的头结点作为Lc的头结点while (pa && pb){if (pa->data <= pb->data){pc->next = pa;pc = pa;pa = pa->next;}else{pc->next = pb;pc = pb;pb = pb->next;}}pc->next = pa ? pa : pb; //插入剩余元素free(*Lb); //释放Lb的头结点*Lb = NULL;
}
二、稀疏多项式的相加和相乘
假设有两个多项式
f 1 ( x ) = 7 + 3 x + 9 x 8 + 5 x 17 f_1(x)=7+3x+9x^8+5x^{17} f1(x)=7+3x+9x8+5x17
f 2 ( x ) = 8 x + 22 x 7 − 9 x 8 f_2(x)=8x+22x^7-9x^8 f2(x)=8x+22x7−9x8
多项式的通项公式为
P n ( x ) = p 1 x e 1 + p 2 x e 2 + ⋯ + p m x e m P_n(x)=p_1x^{e_1}+p_2x^{e_2}+\cdots+p_mx^{e_m} Pn(x)=p1xe1+p2xe2+⋯+pmxem
利用线性表P表示,则
线性表 P = ( ( p 1 , e 1 ) , ( p 2 , e 2 ) , ⋯ , ( p m , e m ) ) 线性表P=((p_1,e_1),(p_2,e_2),\cdots,(p_m,e_m)) 线性表P=((p1,e1),(p2,e2),⋯,(pm,em))
则 f 1 ( x ) 和 f 2 ( x ) 分别用线性表 A 和 B 表示 f_1(x)和f_2(x)分别用线性表A和B表示 f1(x)和f2(x)分别用线性表A和B表示
线性表 A = ( ( 7 , 0 ) , ( 3 , 1 ) , ( 9 , 8 ) , ( 5 , 17 ) ) 线性表A=((7,0),(3,1),(9,8),(5,17)) 线性表A=((7,0),(3,1),(9,8),(5,17))
线性表 B = ( ( 8 , 1 ) , ( 22 , 7 ) , ( − 9 , 8 ) ) 线性表B=((8,1),(22,7),(-9,8)) 线性表B=((8,1),(22,7),(−9,8))
假设使用顺序表实现多项式的相加
算法步骤
- 创建一个新数组c
- 分别从头遍历比较a和b的每一项
指数相同,对应系数相加,若其和为零,则比较两个表的下一项,若其和不为零,则在c中增加一个新项
指数不相同,则将指数比较小的项复制到c中- 一个多项式遍历完毕时,将另一个剩余项依次复制到c中
那么,数组c的大小如何确定?由于无法确定数组c的大小,所以这里不使用顺序表实现,而是用单链表实现。
定义多项式的结点及其结构
//定义多项式结点
struct PolyNode
{float coef; //系数int expn; //指数struct PolyNode* next;
};
//定义多项式结点指针类型
typedef struct PolyNode* PPolyNode;
//定义多项式类型
typedef struct PolyNode* PolyLinkList;
2.1 稀疏多项式的相加
算法步骤:
- 指针p1和p2初始化,分别指向Pa和Pb的首元结点
- p3指向和多项式的当前结点,初值为Pa的头结点
- 当指针p1和p2均为到达表尾时,则循环比较p1和p2所指结点的指数值
- p1->expn 与 p2->expn分3种情况:
当p1->expn == p2->expn是,则将两个结点中的系数相加
若和不为零,则修改p1所指结点的系数值,同时删除p2所指结点
若和为零,则删除p1和p2所指结点
当p1->expn < p2->expn时,则取p1所指结点插入到和多项式链表中
当p1->expn > p2->expn时,则取p2所指结点插入到和多项式链表中- 将非空表的剩余结点插入到p3所指结点的后面
- 释放Pb的头结点
代码实现如下
void poly_add(PolyLinkList* Pa, PolyLinkList* Pb, PolyLinkList* Pc)
{PPolyNode p1 = (*Pa)->next; //指向Pa链表的首元结点PPolyNode p2 = (*Pb)->next; //指向Pb链表的首元结点PPolyNode p3 = *Pa; //指向Pa的头结点,作为和多项式链表 *Pc = *Pa;PPolyNode q = NULL; //指向要被删除的结点 while (p1 && p2){if (p1->expn == p2->expn) //p1指数等于p2指数{float coef = p1->coef + p2->coef;if (coef) //不为零{//修改p1所指结点的系数p1->coef = coef;p3->next = p1;p3 = p1;p1 = p1->next;}else //为零{//删除p1所指结点q = p1;p1 = p1->next;free(q);q = NULL;}//删除p2所指结点q = p2;p2 = p2->next;free(q);q = NULL;} else if (p1->expn < p2->expn) //p1指数小于p2指数{//p1所指结点插入到和多项式链表p3->next = p1;p3 = p1;p1 = p1->next;}else //p1指数大于p2指数{//p2所指结点插入到和多项式链表p3->next = p2;p3 = p2;p2 = p2->next;}}p3->next = p1 ? p1 : p2; //插入剩余数据元素free(*Pb); //释放Pb头结点*Pb = NULL;
}
2.2 稀疏多项式的相乘
- 指针p1和p2初始化,分别指向Pa和Pb的首元结点
- 指针p3初始化,指向Pc的头结点,初化始时,Pc只是一个空表
- 用Pa的第一项与Pb的每一项相乘,将每一项相乘结果插入到Pc中(有序)
- 从Pa的第二项开始与Pb的每一项相乘,将每一项结果插入到Pc中(插入后有序)
在Pc寻找插入位置
设coef = p1->coef * p2->coef ,expn = p1->expn + p2->expn,表示当前p1和p2所指项的相乘结果
若p3->next->expn < expn,则p3 = p3->next,直到p3->next->expn > expn,分两种情况
若存在p3->next->expn > expn, 则新建一个结点插入到p3所指结点后
若不存在p3->next->expn > expn,即p3->next == NULL时,则新建一个结点插入到p3所指结>点后
若p3->next->expn == expn,分两种情况
若p3->next->coef + coef结果为零,则删除p3->next所指结点
若p3->next->coef + coef结果不为零,则修改p3->next所指结点的系数
代码实现如下
//逐项插入法
void poly_mul(PolyLinkList* Pa, PolyLinkList* Pb, PolyLinkList* Pc)
{PPolyNode p1 = (*Pa)->next;PPolyNode p2 = (*Pb)->next; //p1,p2分别指向Pa和Pb的首元结点PPolyNode p3 = *Pc; //p3分别指向Pc的头结点 PPolyNode temp = NULL; //作为一个临时的结点指针if (p1)//将p1的第一项乘以Pb的每一项{while (p2){PPolyNode newNode = (PPolyNode)malloc(sizeof(struct PolyNode));if (NULL == newNode){printf("malloc fail!\n");exit(ERROR);}newNode->coef = p1->coef * p2->coef; //p1,p2所指结点的系数相乘newNode->expn = p1->expn + p2->expn; //p1,p2所指结点的指数相加newNode->next = NULL;p3->next = newNode;p3 = newNode;p2 = p2->next;}}//从Pa的第二项开始与Pb的每一项相乘,将每一项结果插入到Pc,直到p1到达Pa的表尾p1 = p1->next;while (p1){p2 = (*Pb)->next;p3 = *Pc;while (p2){//在Pc寻找插入位置float coef = p1->coef * p2->coef;int expn = p1->expn + p2->expn;while (p3->next && p3->next->expn < expn)p3 = p3->next;if (p3->next && p3->next->expn == expn) //expn与p3->next->expn相同{if (p3->next->coef + coef) //和不为零p3->next->coef += coef;else //和为零{//删除p3->next所指结点temp = p3->next;p3->next = temp->next;free(temp);temp = NULL;}}else //p3->next->expn > expn 或p3->next == NULL{//在p3->next前插入一个新结点temp = (PPolyNode)malloc(sizeof(struct PolyNode));if (NULL == temp){printf("malloc fail!\n");destoryPoly(Pc);}temp->coef = coef;temp->expn = expn;temp->next = p3->next;p3->next = temp;p3 = p3->next;}p2 = p2->next;}p1 = p1->next;}
}
总结
完整代码:https://gitee.com/PYSpring/data-structure/tree/master
相关文章:

数据结构-线性表的应用
目录 前言一、有序表的合并1.1 顺序表实现1.2 单链表实现 二、稀疏多项式的相加和相乘2.1 稀疏多项式的相加2.2 稀疏多项式的相乘 总结 前言 本篇文章介绍线性表的应用,分别使用顺序表和单链表实现有序表的合并,最后介绍如何使用单链表实现两个稀疏多项…...

cpp http server/client
httplib 使用httplib库 basedemo server.cpp #include "httplib.h" #include <iostream> using namespace httplib;int main(void) {Server svr;svr.Get("/hello", [](const Request& req, Response& res) {std::cout << "lo…...

昇思25天学习打卡营第2天|MindSpore快速入门
打卡 目录 打卡 快速入门案例:minist图像数据识别任务 案例任务说明 流程 1 加载并处理数据集 2 模型网络构建与定义 3 模型约束定义 4 模型训练 5 模型保存 6 模型推理 相关参考文档入门理解 MindSpore数据处理引擎 模型网络参数初始化 模型优化器 …...

django之url路径
方式一:path 语法:<<转换器类型:自定义>> 作用:若转换器类型匹配到对应类型的数据,则将数据按照关键字传参的方式传递给视图函数 类型: str: 匹配除了”/“之外的非空字符串。 /test/zvxint: 匹配0或任何…...

【OnlyOffice】桌面应用编辑器,插件开发大赛,等你来挑战
OnlyOffice,桌面应用编辑器,最近版本已从8.0升级到了8.1 从PDF、Word、Excel、PPT等全面进行了升级。随着AI应用持续的火热,OnlyOffice也在不断推出AI相关插件。 因此,在此给大家推荐一下OnlyOffice本次的插件开发大赛。 详细信息…...

[学习笔记]SQL学习笔记(连载中。。。)
学习视频:【数据库】SQL 3小时快速入门 #数据库教程 #SQL教程 #MySQL教程 #database#Python连接数据库 目录 1.SQL的基础知识1.1.表(table)和键(key)1.2.外键、联合主键 2.MySQL安装(略,请自行参考视频)3.基本的MySQL语法3.1.规…...

Buuctf之SimpleRev做法
首先,查个壳,64bit,那就丢进ida64中进行反编译进来之后,我们进入main函数,发现里面没什么东西,那就shiftf12搜索字符串,找到关键字符串,双击进入然后再选中该字符串,ctrl…...
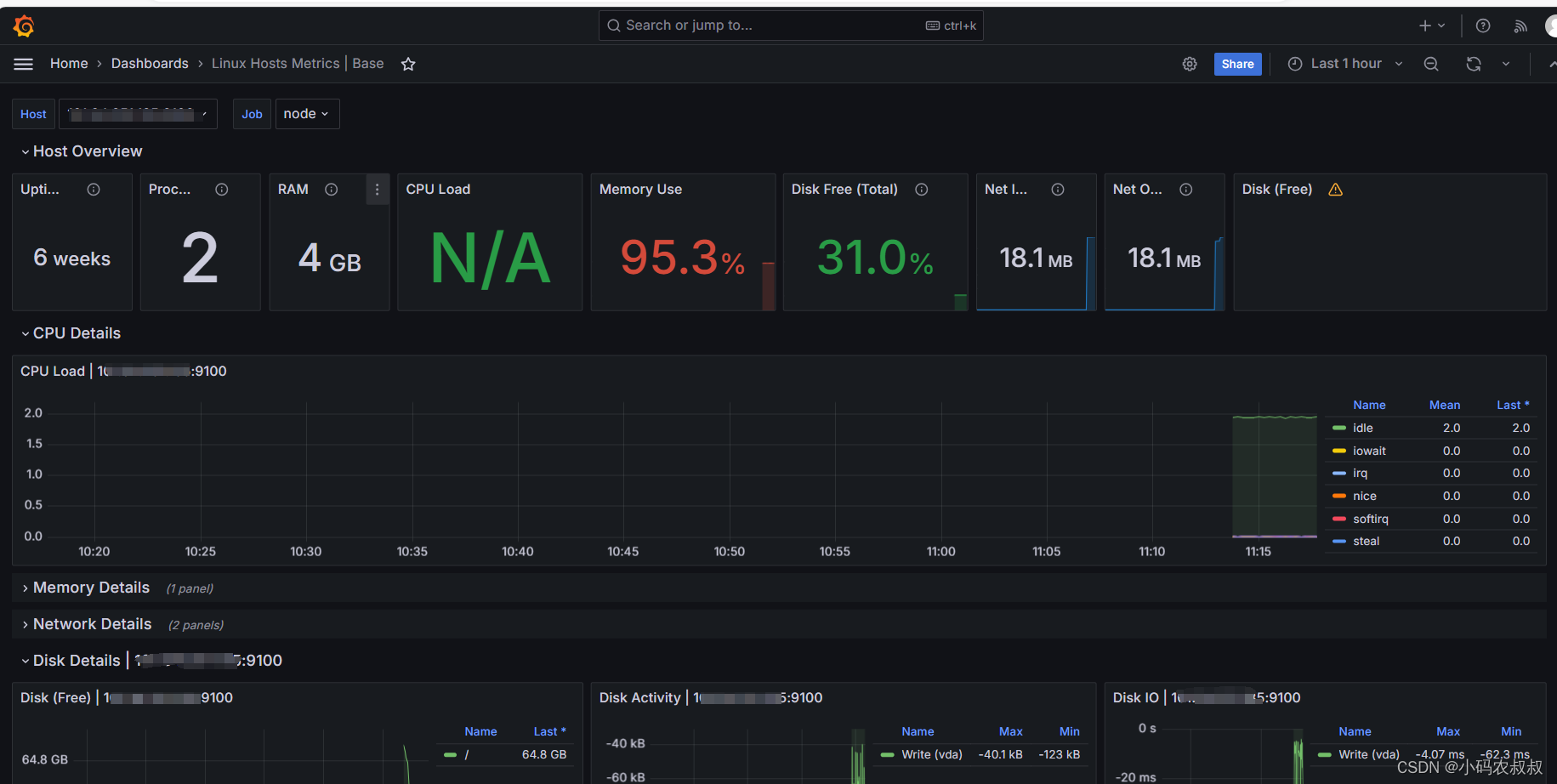
【云原生监控】Prometheus 普罗米修斯从搭建到使用详解
目录 一、前言 二、服务监控概述 2.1 什么是微服务监控 2.2 微服务监控指标 2.3 微服务监控工具 三、Prometheus概述 3.1 Prometheus是什么 3.2 Prometheus 特点 3.3 Prometheus 架构图 3.3.1 Prometheus核心组件 3.3.2 Prometheus 工作流程 3.4 Prometheus 应用场景…...

【C++】模板进阶--保姆级解析(什么是非类型模板参数?什么是模板的特化?模板的特化如何应用?)
目录 一、前言 二、什么是C模板? 💦泛型编程的思想 💦C模板的分类 三、非类型模板参数 ⚡问题引入⚡ ⚡非类型模板参数的使用⚡ 🔥非类型模板参数的定义 🔥非类型模板参数的两种类型 ὒ…...

Cookie与Session
Cookie Set-Cookie: sessionIdabc123; ExpiresWed, 09 Jun 2024 10:18:14 GMT; Path/; Secure; HttpOnlySession session作用域 首先需要了解servlet容器可能包含多个web应用。 在servlet容器中同一应用的servlet 对 session数据是可见的,不同应用之间session是相互…...

Nuxt3 的生命周期和钩子函数(十一)
title: Nuxt3 的生命周期和钩子函数(十一) date: 2024/7/5 updated: 2024/7/5 author: cmdragon excerpt: 摘要:本文详细介绍了Nuxt3中几个关键的生命周期钩子和它们的使用方法,包括webpack:done用于Webpack编译完成后执行操作…...

Windows ipconfig命令详解,Windows查看IP地址信息
「作者简介」:冬奥会网络安全中国代表队,CSDN Top100,就职奇安信多年,以实战工作为基础著作 《网络安全自学教程》,适合基础薄弱的同学系统化的学习网络安全,用最短的时间掌握最核心的技术。 ipconfig 1、基…...
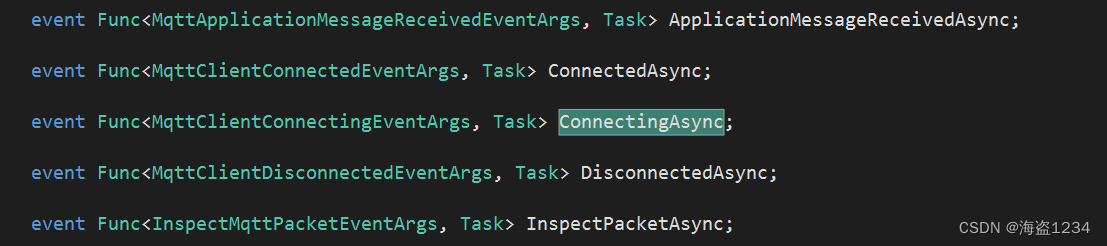
在C#/Net中使用Mqtt
net中MQTT的应用场景 c#常用来开发上位机程序,或者其他一些跟设备打交道比较多的系统,所以会经常作为拥有数据的终端,可以用来采集上传数据,而MQTT也是物联网常用的协议,所以下面介绍在C#开发中使用MQTT。 安装MQTTn…...

VBA提取word表格内容到excel
这是一段提取word表格中部分内容的vb代码。 Sub 提取word表格() mypath ThisWorkbook.Path & "\"myname Dir(mypath & "*.doc*")n 4 index of rowsRange("A1:F1") Array("课程代码", "课程名称", "专业&…...
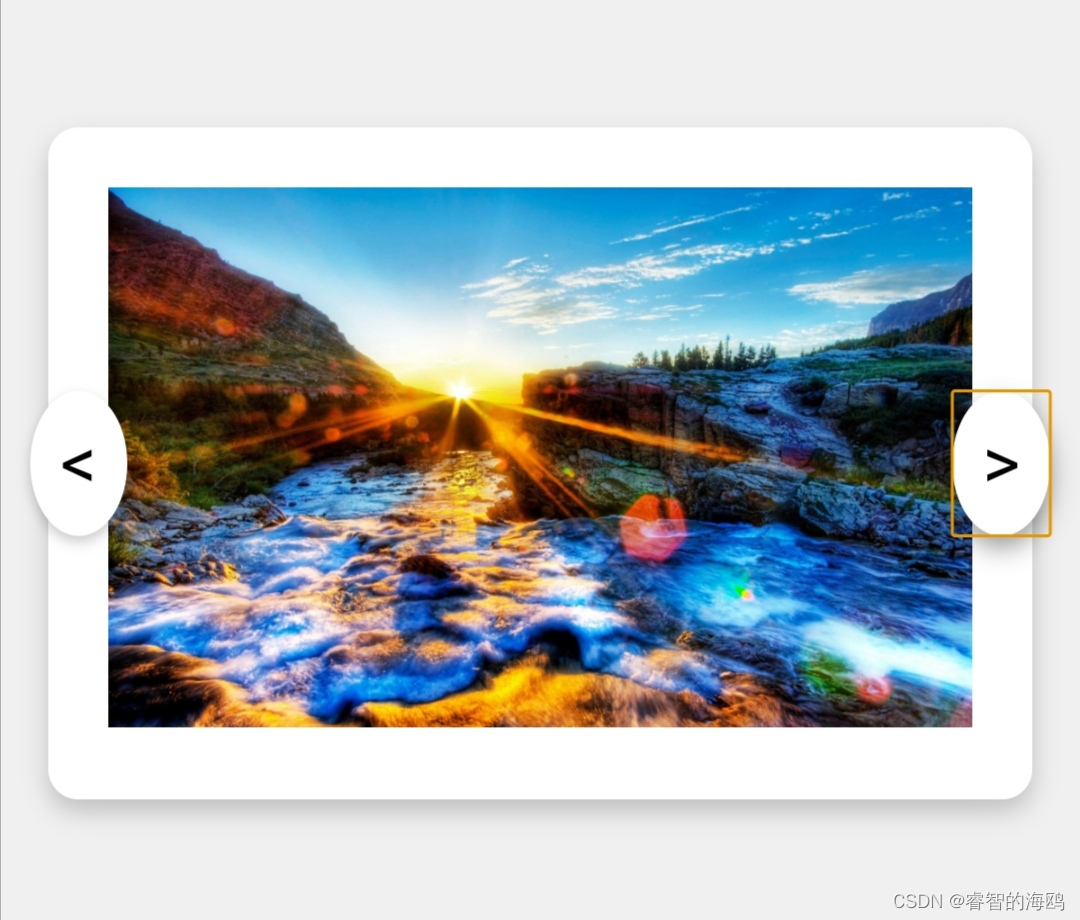
html+css+js图片手动轮播
源代码在界面图片后面 轮播演示用的几张图片是Bing上的,直接用的几张图片的URL,谁加载可能需要等一下,现实中替换成自己的图片即可 关注一下点个赞吧😄 谢谢大佬 界面图片 源代码 <!DOCTYPE html> <html lang&quo…...

【十三】图解 Spring 核心数据结构:BeanDefinition 其二
图解 Spring 核心数据结构:BeanDefinition 其二 概述 前面写过一篇相关文章作为开篇介绍了一下BeanDefinition,本篇将深入细节来向读者展示BeanDefinition的设计,让我们一起来揭开日常开发中使用的bean的神秘面纱,深入细节透彻理解…...

数据库作业
命令 登陆数据库 mysql -uroot -p123456 --prompt"\u\h:\d--> " 创建数据库zcr create database zcr; 修改数据库zcr字符集为gbk alter database zcr default character set gbk collate gbk_chinese_ci; 选择数据库zcr use zcr 查看数据库zc…...

12、matlab中for循环,if else判断语句,break和continue用法以及switch case语句使用
1、前言 在MATLAB中,for循环用于迭代一个固定次数的循环。可以使用if else语句在循环中进行条件判断,根据条件的不同执行相应的代码块。break和continue可以用于控制循环的执行流程,break用于提前结束循环,而continue用于跳过当前…...

AcWing 3207:门禁系统 ← 桶排序中“桶”的思想
【题目来源】https://www.acwing.com/problem/content/3210/【题目描述】 涛涛最近要负责图书馆的管理工作,需要记录下每天读者的到访情况。 每位读者有一个唯一编号,每条记录用读者的编号来表示。 给出读者的来访记录,请问每一条记录中的读者…...

开发个人Go-ChatGPT--3 服务拆分
开发个人Go-ChatGPT–3 服务拆分 个人Go-ChatGPT项目可拆分用户服务(user),AI模型服务(AiModel),… 每个服务都可以再分为 api 服务和 rpc 服务。api 服务对外,可提供给 app 调用。rpc 服务是…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...
