IDA*——AcWing 180. 排书
IDA*
定义
IDA*(Iterative Deepening A*)是一种结合了深度优先搜索(DFS)的递归深度限制特性和A搜索的启发式估价函数的搜索算法。它主要用于解决启发式搜索问题,尤其是当搜索空间很大或者搜索成本不确定时。
IDA* 是一种最佳优先搜索算法,其基本思想是在深度优先搜索的基础上,通过逐步增加搜索深度并结合A*算法中的估价函数f(n)=g(n)+h(n),来找到从初始节点到目标节点的最短路径。其中,g(n)是从初始节点到当前节点的实际代价,h(n)是从当前节点到目标节点的启发式估计代价。
运用情况
- 内存限制: IDA特别适合那些内存有限制的环境,因为它不像A那样需要维护一个开放列表(open list),而是采用递归的方式逐步深入搜索。
- 未知或变化的成本: 当搜索空间中节点的移动成本不是预先完全已知或可能变化时,IDA*通过逐步探索来适应这种不确定性。
- 最优解搜索: 当寻找问题的最优解而非任一解时,IDA*通过其最佳优先的特性保证找到的是从起点到终点的最短路径。
- 大型或无限状态空间: 对于状态空间非常大或理论上无限的情况,IDA*通过逐步加深搜索深度来逐步逼近解,避免了一次性需要大量内存来存储整个搜索树的问题。
注意事项
- 启发式函数的选择: h(n)的选择至关重要,它需要保证不大于实际的最小代价,否则算法可能不会终止。理想的h(n)接近实际成本但又易于计算。
- 深度限制: 初始时设置一个合理的深度限制,随着搜索的进行逐渐增加,直到找到解或达到某个预设的深度上限。
- 效率: 虽然IDA避免了A中的开放列表维护,但如果启发式不够好或搜索空间极大,递归调用可能会导致大量的重复计算和较慢的收敛速度。
- 栈溢出风险: 由于使用递归,如果搜索深度过大,可能会导致栈溢出。在实现时可以考虑使用迭代版本来避免这一问题。
解题思路
- 初始化: 设定初始深度限制d=0,以及一个足够大的上限D作为退出条件。
- 计算阈值: 使用当前深度限制计算f(n)的阈值,即f_limit = g(start) + d * h(start),其中g(start)=0,因为是从初始节点开始。
- 深度优先搜索: 从初始节点开始执行深度优先搜索,只有当节点的f(n)=g(n)+h(n)小于当前的f_limit时才继续扩展该节点的子节点。
- 递归加深: 如果在当前深度限制下没有找到解,则增加深度限制d=d+1,回到步骤2,继续搜索。
- 结束条件: 当搜索到目标节点或达到预设的深度上限D时,结束搜索。
AcWing 180. 排书
题目描述
180. 排书 - AcWing题库

运行代码
#include <iostream>
#include <cstring>
#include <algorithm>
const int N = 15; // 书的数量上限
using namespace std;
int n; // 实际的书的数量
int q[N]; // 存储书的初始排列
int w[5][N]; // 辅助数组,用于在搜索过程中保存中间状态
// 估价函数:计算当前状态与目标状态的差异,返回还需要多少步才能达到目标状态
int f() { int tot = 0;for (int i = 0; i + 1 < n; ++i) {if (q[i + 1]!= q[i] + 1) {++tot;}}return (tot + 2) / 3;
}
// 深度优先搜索函数
bool dfs(int depth, int max_depth) { if (depth + f() > max_depth) { // 如果当前深度加上估计的剩余深度超过了限制深度,进行剪枝return false; }if (f() == 0) { // 如果估价函数为0,说明已经达到目标状态return true; }for (int len = 1; len < n; ++len) { // 枚举要移动的连续段的长度for (int l = 0; l + len - 1 < n; ++l) { // 枚举连续段的起始位置int r = l + len - 1; for (int k = r + 1; k < n; ++k) { // 枚举要插入的位置(连续段的结束位置的后面)memcpy(w[depth], q, sizeof q); // 复制当前状态到辅助数组int y = l; for (int x = r + 1; x <= k; x++, y++) { // 将连续段插入到指定位置q[y] = w[depth][x]; }for (int x = l; x <= r; x++, y++) {q[y] = w[depth][x]; }if (dfs(depth + 1, max_depth)) { // 递归搜索下一层return true; }memcpy(q, w[depth], sizeof q); // 如果不成功,恢复当前状态 }}}return false;
}
int main() { int T; cin >> T; while (T--) { cin >> n; for (int i = 0; i < n; ++i) {cin >> q[i]; }int depth = 0; // 迭代加深搜索,从深度0开始,每次增加1,直到找到解或者深度达到5while (depth < 5 &&!dfs(0, depth)) { depth++; }if (depth >= 5) {cout << "5 or more" << endl; } else {cout << depth << endl; }}return 0;
}代码思路
- 估价函数
f():用于估计从当前状态到达目标状态(书按照1∼n的顺序依次排列)还需要的最少操作次数。通过计算当前排列中顺序不正确的后继关系的数量tot,然后返回(tot + 2) / 3作为估计值。这是因为每次移动一个连续段最多可以改变 3 个元素的后继关系。 dfs(int depth, int max_depth)函数:进行深度优先搜索。- 参数
depth表示当前搜索的深度(即已经进行的操作次数)。 max_depth是限制的最大深度。如果在当前深度depth下,加上估计的还需要的最少操作次数f()超过了max_depth,就意味着即使后面按照最优方式操作也无法在限制深度内达到目标状态,此时进行剪枝(直接返回false,不再继续搜索该路径)。- 通过三重循环来枚举移动连续段的长度、起始位置和插入位置,模拟进行抽取连续段并插入到其他位置的操作。
- 在每次尝试一种可能的操作后,递归调用
dfs(depth + 1, max_depth)搜索下一层。如果找到解(即达到目标状态),则返回true,否则恢复原来的状态(通过memcpy(q, w[depth], sizeof q);),继续尝试其他可能的操作。
- 参数
- 主函数中的迭代加深搜索:从深度 0 开始,每次增加 1,调用
dfs(0, depth)进行搜索。如果在深度小于等于 4 时找到了解,就输出对应的操作次数;如果直到深度达到 5 还没有找到解,就输出"5 or more"。
改进思路
- 优化内存使用:可以减少使用的辅助数组数量,或者使用更高效的数据结构来存储中间状态。
- 改进剪枝策略:可以进一步优化估价函数,使其更加准确,从而增强剪枝效果,减少不必要的搜索。
- 优化循环结构:对于一些循环的边界条件和步长进行优化,以减少不必要的计算。
改进代码
#include <iostream>
#include <cstring>
#include <algorithm>const int N = 15; // 书的数量上限int n; // 实际的书的数量
int q[N]; // 存储书的初始排列// 估价函数:计算当前状态与目标状态的差异,返回还需要多少步才能达到目标状态
int f() { int tot = 0;for (int i = 0; i + 1 < n; ++i) {if (q[i + 1]!= q[i] + 1) {++tot;}}return (tot + 2) / 3;
} // 深度优先搜索函数
bool dfs(int depth, int max_depth) { if (depth + f() > max_depth) { // 如果当前深度加上估计的剩余深度超过了限制深度,进行剪枝return false; }if (f() == 0) { // 如果估价函数为0,说明已经达到目标状态return true; }for (int len = 1; len < n; ++len) { // 枚举要移动的连续段的长度for (int l = 0; l + len - 1 < n; ++l) { // 枚举连续段的起始位置int r = l + len - 1; for (int k = r + 1; k < n; ++k) { // 枚举要插入的位置(连续段的结束位置的后面)int temp[N];memcpy(temp, q, sizeof(q)); // 复制当前状态int y = l; for (int x = r + 1; x <= k; x++, y++) { // 将连续段插入到指定位置q[y] = temp[x]; }for (int x = l; x <= r; x++, y++) {q[y] = temp[x]; }if (dfs(depth + 1, max_depth)) { // 递归搜索下一层return true; }memcpy(q, temp, sizeof(q)); // 如果不成功,恢复当前状态 }}}return false;
} int main() { int T; std::cin >> T; while (T--) { std::cin >> n; for (int i = 0; i < n; ++i) {std::cin >> q[i]; }int depth = 0; // 迭代加深搜索,从深度0开始,每次增加1,直到找到解或者深度达到5while (depth < 5 &&!dfs(0, depth)) { depth++; }if (depth >= 5) {std::cout << "5 or more" << std::endl; } else {std::cout << depth << std::endl; }}return 0;
}相关文章:

IDA*——AcWing 180. 排书
IDA* 定义 IDA*(Iterative Deepening A*)是一种结合了深度优先搜索(DFS)的递归深度限制特性和A搜索的启发式估价函数的搜索算法。它主要用于解决启发式搜索问题,尤其是当搜索空间很大或者搜索成本不确定时。 IDA* 是…...

【云计算】公有云、私有云、混合云、社区云、多云
公有云、私有云、混合云、社区云、多云 1.云计算的形态1.1 公有云1.2 私有云1.3 混合云1.4 社区云1.5 多云1.5.1 多云和混合云之间的关系1.5.2 多云的用途1.5.3 影子 IT 和多云1.5.4 优缺点 2.不同云形态的对比 1.云计算的形态 张三⾃⼰在家做饭吃,这是 私有云&…...

MySQL中的MVCC解析
MySQL中的MVCC解析 多版本并发控制是MySQL中实现高并发的一种关键技术。通过对数据进行多版本的管理,MVCC能够在保证数据一致性的同时,提高数据库的并发性能。本文将深入探讨MySQL中的MVCC机制,包括其原理、实现方式以及优势。 MVCC的原理 …...

【2024最新华为OD-C/D卷试题汇总】[支持在线评测] LYA的生日聚会(100分) - 三语言AC题解(Python/Java/Cpp)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员 ✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解 💻 ACM银牌🥈| 多次AK大厂笔试 | 编程一对一辅导 👏 感谢大家的订阅➕ 和 喜欢💗 …...

初识STM32:芯片基本信息
STM32简介 STM32是ST公司基于ARM公司的Cortex-M内核开发的32位微控制器。 ARM公司是全球领先的半导体知识产权(IP)提供商,全世界超过95%的智能手机和平板电脑都采用ARM架构。 ST公司于1987年由意大利的SGS微电子与法国的Thomson半导体合并…...
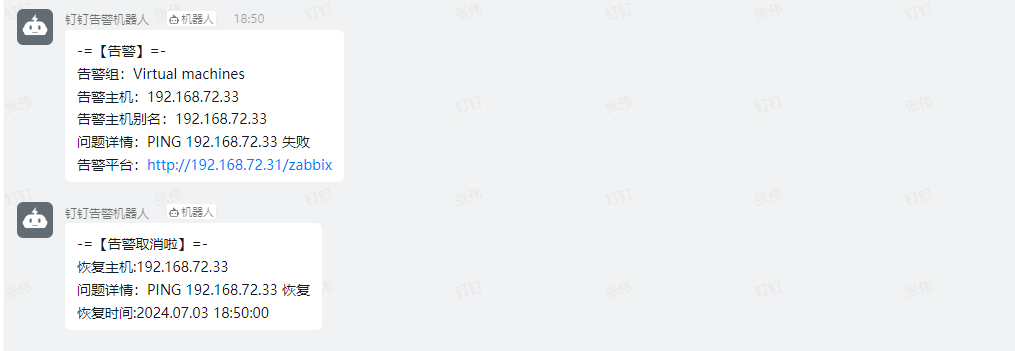
Zabbix 配置PING监控
Zabbix PING监控介绍 如果需要判断机房的网络或者主机是否正常,这就需要使用zabbix ping,Zabbix使用外部命令fping处理ICMP ping的请求,在基于ubuntu APT方式安装zabbix后默认已存在fping程序。另外zabinx_server配置文件参数FpingLocation默…...
-- Wandb fails with ServiceStartProcessError)
异常解决(三)-- Wandb fails with ServiceStartProcessError
原文链接:https://github.com/wandb/wandb/issues/5765 我的环境配置: Python3.8.16 Wandb0.17.4 在使用Wandb记录实验数据时, 报以下错误: ServiceStartProcessError: The wandb service process exited with 1. Ensure that s…...
)
Qt调用Matlab(一)
目录 1 概述2 创建Qt工程2.1 增加Matlab支持3 调用Matlab3.1 widget.h3.2 widget.cpp4 运行4.1 配置4.2 运行1 概述 MATLAB是MathWorks公司出品的商业数学软件,用于数据分析、无线通信、深度学习、图像处理与计算机视觉、信号处理、量化金融与风险管理、机器人,控制系统等领域…...

网络爬虫(二) 哔哩哔哩热榜高频词按照图片形状排列
我们有时候需要爬取结果生成为自定义的词云图 生成自定义的词云图通常需要以下步骤: 1. 爬取数据:使用爬虫工具或库,如requests、BeautifulSoup等,可以爬取网页、论坛、社交媒体等平台上的文本数据。 2. 数据预处理:…...

MySQL 常见错误及解决方案
1. Too many connections 运行环境:Winows11、Phpstudy V8.1.1.3、MySQL 5.7.26 同一时间 MySQL 的连接数量有限制,当超过上限时将提示下面错误信息: 1040 - Too many connections 查看当前最大连接数 mysql> show variables like %max_…...

STM32 - 内存分区与OTA
最近搞MCU,发现它与SOC之间存在诸多差异,不能沿用SOC上一些技术理论。本文以STM L4为例,总结了一些STM32 小白入门指南。 标题MCU没有DDR? 是的。MCU并没有DDR,而是让代码存储在nor flash上,临时变量和栈…...

RAG理论:ES混合搜索BM25+kNN(cosine)以及归一化
接前一篇:RAG实践:ES混合搜索BM25+kNN(cosine) https://blog.csdn.net/Xin_101/article/details/140230948 本文主要讲解混合搜索相关理论以及计算推导过程, 包括BM25、kNN以及ES中使用混合搜索分数计算过程。 详细讲解: (1)ES中如何通过BM25计算关键词搜索分数; (2)…...
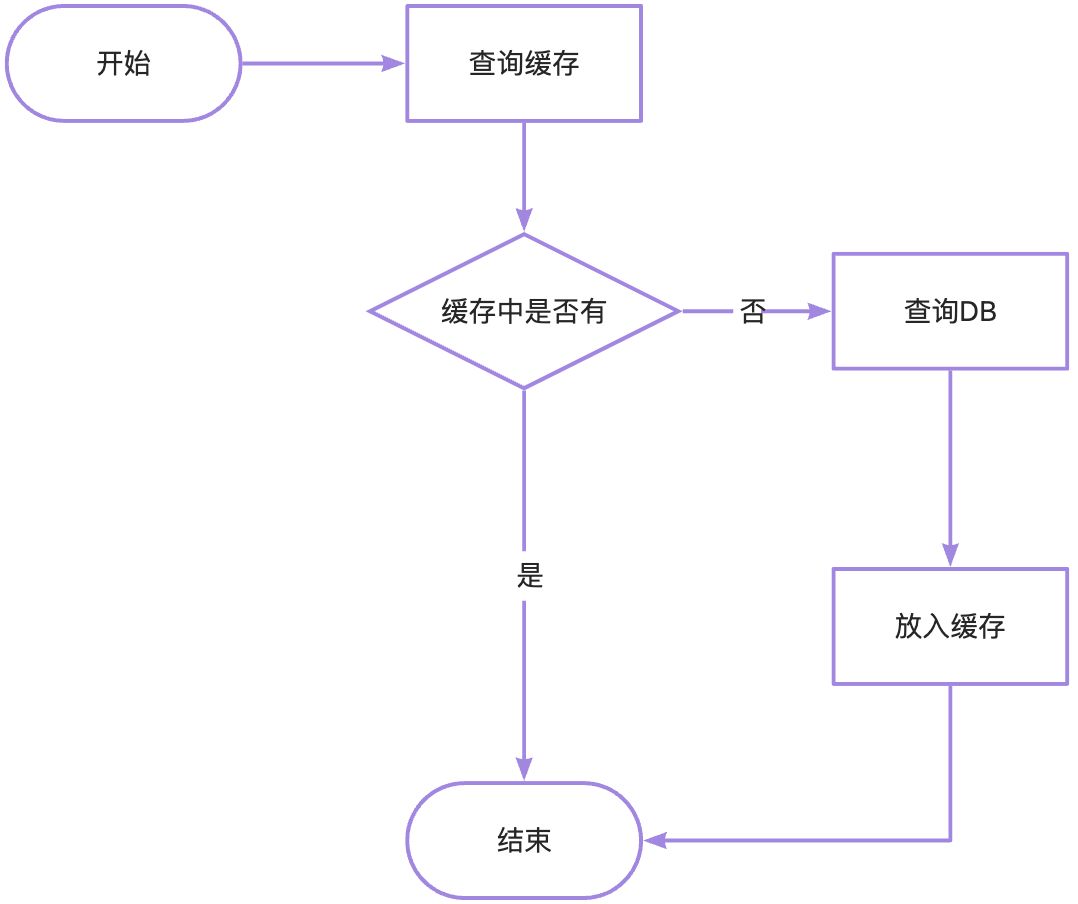
分享大厂对于缓存操作的封装
hello,伙伴们好久不见,我是shigen。发现有两周没有更新我的文章了。也是因为最近比较忙,基本是993了。 缓存大家再熟悉不过了,几乎是现在任何系统的标配,并引申出来很多的问题:缓存穿透、缓存击穿、缓存雪崩…...

冯诺依曼体系结构与操作系统(Linux)
文章目录 前言冯诺依曼体系结构(硬件)操作系统(软件)总结 前言 冯诺依曼体系结构(硬件) 上图就是冯诺依曼体系结构图,主要包括输入设备,输出设备,存储器,运算…...

开源六轴协作机械臂myCobot280实现交互式乘法!让学习充满乐趣
本文经作者Fumitaka Kimizuka 授权我们翻译和转载。 原文链接:myCobotに「頷き」「首振り」「首傾げ」をしてもらう 🤖 - みかづきブログ・カスタム 引言 Fumitaka Kimizuka 创造了一个乘法表系统,帮助他的女儿享受学习乘法表的乐趣。她可以…...

[C++][CMake][嵌套的CMake]详细讲解
目录 0.前言 & 准备1.节点关系2.添加子目录3.解决问题1.根目录2.calc目录3.sort目录4.calc_test目录5.sort_test 4.注意 0.前言 & 准备 如果项目很大,或者项目中有很多的源码目录,在通过CMake管理项目的时候如果只使用一个CMakeLists.txt&#…...

尚品汇-(十三)
(1)查询sku列表 在ManageService 中添加 /*** SKU分页列表* param pageParam* return*/ IPage<SkuInfo> getPage(Page<SkuInfo> pageParam);接口实现类 Override public IPage<SkuInfo> getPage(Page<SkuInfo> pageParam) {Qu…...
python小练习04
三国演义词频统计与词云图绘制 import jieba import wordcloud def analysis():txt open("三国演义.txt",r,encodingutf-8).read()words jieba.lcut(txt)#精确模式counts {}for word in words:if len(word) 1:continueelif word "诸葛亮" or word &q…...

小试牛刀-Solana合约账户详解
目录 一.Solana 三.账户详解 3.1 程序账户 3.2 系统所有账户 3.3 程序派生账户(PDA) 3.4 Token账户 四、相关学习文档 五、在线编辑器 Welcome to Code Blocks blog 本篇文章主要介绍了 [Solana合约账户详解] ❤博主广交技术好友,喜欢文章的可以关注一下❤ …...

Spring Boot+Vue项目从零入手
Spring BootVue项目从零入手 一、前期准备 在搭建spring bootvue项目前,我们首先要准备好开发环境,所需相关环境和软件如下: 1、node.js 检测安装成功的方法:node -v 2、vue 检测安装成功的方法:vue -V 3、Visu…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

归并排序:分治思想的高效排序
目录 基本原理 流程图解 实现方法 递归实现 非递归实现 演示过程 时间复杂度 基本原理 归并排序(Merge Sort)是一种基于分治思想的排序算法,由约翰冯诺伊曼在1945年提出。其核心思想包括: 分割(Divide):将待排序数组递归地分成两个子…...

【阅读笔记】MemOS: 大语言模型内存增强生成操作系统
核心速览 研究背景 研究问题:这篇文章要解决的问题是当前大型语言模型(LLMs)在处理内存方面的局限性。LLMs虽然在语言感知和生成方面表现出色,但缺乏统一的、结构化的内存架构。现有的方法如检索增强生成(RA…...

云原生时代的系统设计:架构转型的战略支点
📝个人主页🌹:一ge科研小菜鸡-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、云原生的崛起:技术趋势与现实需求的交汇 随着企业业务的互联网化、全球化、智能化持续加深,传统的 I…...
