017-GeoGebra基础篇-微积分函数求解圆弧面积问题
基础篇慢慢的走进尾声,今天给大家带来一个小项目,是关于高中数学微积分部分的展示,这个项目主要包含了函数的介绍、函数与图形绘制的区别、区域函数图像的绘制、积分函数的应用、动态文本的调用、嵌套滑动条的应用等等,以及其他常用的技能和比较容易踩到的坑。那就,开始吧!
目录
- 一、项目展示
- 1. 项目目标
- 2. 逐步绘制出第i个小矩形动图展示
- 3. 增加小矩形个数后的动图展示
- 二、涉及内容
- 三、项目步骤
- 1. 编写解析式;
- 2. 制作分段函数;
- 3. 制作嵌套滑动条;
- 4. 设置曲线上的点A;
- 5. 积分函数的使用;
- 6. 动态文本的插入;
- 7. 项目嵌入PPT;
- 四、关于函数与表达式
- 1. 什么是函数,什么是表达式?
- 2. 函数和表达式有什么区别
- 五、文章最后
一、项目展示
因为项目已经不是一两个功能,所以简要说明一下还是有必要的!
1. 项目目标
- 将圆弧与X轴之间的面积划分为N个小矩形,N可以动态调节;
- 绘制矩形要同时包含外围绘制和内围绘制;
- 逐步绘制出第i个小矩形;
- 计算0-i个小矩形的面积,动态显示;
- 计算外围小矩形面积总和与内围小矩形面积总和之差;
- 颜色搭配合理、布局清晰;
- 最终结果插入PPT中,播放时进行交互式操作。
2. 逐步绘制出第i个小矩形动图展示

3. 增加小矩形个数后的动图展示

二、涉及内容
- 函数解析式的使用;
- 分段函数的使用;
- 嵌套滑动条的制作;
- 圆弧上动点的绘制;
- 积分函数的使用;
- 动态文本的调用。
三、项目步骤
1. 编写解析式;
f(x)=sqrt(1-x^(2))
g(x)=-sqrt(1-x^(2))

上边的弧形用来做积分图像,下边的弧形形用来做分段函数(只有上边一半不会很好看,起到衬托补全的作用)
2. 制作分段函数;
h(x)=If(-1≤x≤-0.6, g(x), ?)
p(x)=If(0.6≤x≤1, g(x), ?)


分段函数可以使用If语句进行操作,If(条件表达式,若是真该怎么办,若是假该怎么办),这样就可以完美实现不要[-0.6,0.6]这部分的图像。
3. 制作嵌套滑动条;

注意,滑动条可以进行嵌套操作,也就是说,上一个条的值,可以作为这个滑动条的最大值或者最小值(比如上边的滑动条标签是n,那我们可以直接将第二个滑动条的最大值设置为n);
4. 设置曲线上的点A;
A=(((i)/(n))*2-1,f(((i)/(n))*2-1))
i_{1}: PerpendicularLine(A,xAxis)

注意:这里有一个逻辑难点,如何根据“正在绘制的第i个矩形”,计算出“第i个矩形弧线上点的位置”,也就是点A。
- n当前是总的细分矩形个数;
- i是当前正在绘制的第i个矩形;
- i/n就是绘制完成的比例,用这个比例乘以(-1,0)和(1,0)之间的距离,就是点A从(-1,0)移动的距离在X轴的投影长度;
- 那么就可以计算出A点的横坐标:((i)/(n))*2-1;
- 将横坐标代入到f(x)中,可以得到点A的坐标:(((i)/(n))*2-1,f(((i)/(n))*2-1)),这个坐标始终都在弧线f(x)上。
可能有人好奇为什么要设置点A,因为我们要用到点A的横坐标来卡积分的范围,一起继续往下看。
5. 积分函数的使用;
S1=UpperSum(f(x),-1,x(A),i)
S2=LowerSum(f(x),-1,x(A),i)

S1 是外围积分,S2是内围积分,积分函数很简单,但是需要看清楚里边的参数设置(函数,起始位置,终止位置,细分段数)
注意,第一个是函数,而不是表达式(区别会在文章末尾单独列出)
6. 动态文本的插入;
动态文本的插入在之前的文章写过,具体可以见编号015,这里简单过一下。

- 这里虽然是用+号连接符连接起来的变量,但是强烈不建议在这里直接写,有几个坑需要注意;
- 直接输入中文有时候会输入不进去,这是个bug;
- 如果直接在这里写,中英文切换时会产生错误符号,最终导致算式编写失败;
- 建议先选择文本输入,然后写上111占位就可以了。

写完111后默认是隐藏的,点击前面的小圆形即可显示文本,然后双击文本进行编辑;



唯一需要注意的是,这个地方可以写公式,也可以输入特殊符号


7. 项目嵌入PPT;
嵌入PPT的操作也不过多赘述了哈,可以参见文章编号003,里边介绍了如何将GeoGebra无缝嵌入到PPT里。
四、关于函数与表达式
1. 什么是函数,什么是表达式?
越高级的函数,里边的参数就越强调使用函数,而不是表达式,如果使用表达式软件就会进行无休止的报错,那么什么是什么是函数,什么是表达式?
(1)这个是函数

有自变量,有因变量,这个是函数。
(2)这个是表达式

直接绘制出来一个圆,没有把因变量单独取出来,这个叫表达式
2. 函数和表达式有什么区别
老实说没有什么区别,毕竟两者可以相互转换,但是对于GeoGebra来说,区别可就大了,因为前者可以作为其他函数的参数,后者就只能绘制一个图形,对于积分函数而言,它的第一个参数就要求使用函数。
其他特点可以参考这个表格:
| 特点 | 函数 | 表达式 |
|---|---|---|
| 特点 | 精确:这种方法非常精确,允许用户通过精确的数学表达式定义圆的半径、位置等属性。 代数表达:这种方法属于代数表达方式,适合需要通过代数式精确定义图形的场景。 不易调整:由于是通过代数式定义的,调整圆的属性需要修改代数表达式,而不是通过鼠标拖动。 | 直观:这种方法非常直观,可以通过鼠标点击直接定义圆的位置和大小。 这种方法属于几何构造方式,适合需要通过可视化操作绘制图形的场景。 通过拖动定义点,可以手动调整圆的大小和位置。 |
| 应用场景 | 适用于需要精确绘制圆的情况,尤其是在数学建模、函数图像绘制等需要精确控制图形属性的场景中。 | 适用于需要快速、直观绘制圆的情况,尤其是在需要根据特定点来确定圆的位置和大小时。 |
总之呢,表达式作图适合需要直观、快速绘制的场景,操作简单,适用于几何构造和可视化调整。通过函数作图,适合需要精确控制图的属性,适用于数学建模和函数图像绘制。
五、文章最后
本篇文章内容稍微有些复杂,这里已经将源文件进行保存,若有需要欢迎自取,告诉客F领一下017号文件即可。

当然,若有任何问题都可以在这个铺子询问,也会有资源相送,GeoGebra、PPT、平面动画、3D动画等各种技术都可以,祝好!

相关文章:

017-GeoGebra基础篇-微积分函数求解圆弧面积问题
基础篇慢慢的走进尾声,今天给大家带来一个小项目,是关于高中数学微积分部分的展示,这个项目主要包含了函数的介绍、函数与图形绘制的区别、区域函数图像的绘制、积分函数的应用、动态文本的调用、嵌套滑动条的应用等等,以及其他常…...
Element中的选择器组件Select (一级选择组件el-select)
简述:在 Element UI 中,ElSelect(或简称为 Select)是一个非常常用的选择器组件,它提供了丰富的功能来帮助用户从一组预定义的选项中选择一个或多个值。这里来简单记录一下 一. 组件和属性配置 <el-selectv-model&q…...

数值分析笔记(五)线性方程组解法
三角分解法 A的杜利特分解公式如下: u 1 j a 1 j ( j 1 , 2 , ⋯ , n ) , l i 1 a i 1 / u 11 ( i 2 , 3 , ⋯ , n ) , u k j a k j − ∑ m 1 k − 1 l b m u m j ⇒ a k j ( j k , k 1 , ⋯ , n ) , l i k ( a i k − ∑ m 1 k − 1 l i n u m k ) /…...
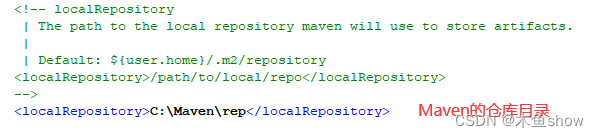
IDEA中Maven的配置
目录 1. 安装maven 2. 配置环境变量 3. IDEA中配置Maven 4. 配置仓库目录 1. 安装maven 官网下载地址:Maven – Download Apache Maven 下载后,将zip压缩包解压到某个目录即可。 2. 配置环境变量 变量名称随意,通常为M2_HOMEÿ…...

成人高考本科何时报名-深职训学校帮您规划学习之路
你有想过继续深造自己的学历吗?也许你已经工作多年,但总觉得学历是一块心病,想要通过成人高考本科来提升自己。不用着急,今天我们来聊一聊成人高考本科的报名时间,以及深职训学校如何帮助你顺利完成报名。 深圳成人高…...
)
C++ STL 协程(Coroutines)
一:什么是协程(Coroutines): 协程是轻量级线程,可以暂停和恢复执行,协程拥有自己的暂停点状态,协程暂停时,将当前状态保存起来,在恢复执行时会恢复之前保存的状态。 二:例子: #include <coroutine> #include <iostream>void doTheWork() {std::cout <…...

虚拟机下基于海思移植QT(一)——虚拟机下安装QT
0.参考资料 1.海思Hi3516DV300 移植Qt 运行并在HDMI显示器上显示 2.搭建海思3559A-Qt4.8.7Openssl开发环境 1.报错解决 通过下面命令查询 strings /lib/x86_64-linux-gnu/libc.so.6 | grep GLIBC_通过命令行没有解决: sudo apt install libc6-dev libc6参考解决…...

计算机网络部分知识点整理
停止等待协议的窗口尺寸为 1。 √以太网标准是IEEE802.3TCP/IP四层,OSI模型有7层,地址解析协议 ARP 在 OSI 参考七层协议属于数据链路层,在TCP/IP 协议属于网络层,ARP作用:将 IP 地址映射到第二层地址,交换…...

【Qt】Qt概述
目录 一. 什么是Qt 二. Qt的优势 三. Qt的应用场景 四. Qt行业发展方向 一. 什么是Qt Qt是一个跨平台的C图形用户界面应用程序框架,为应用程序开发者提供了建立艺术级图形界面所需的所有功能。 Qt是完全面向对象的,很容易扩展,同时Qt为开发…...

读书笔记-《魔鬼经济学》
这是一本非常有意思的经济学启蒙书,作者探讨了许多问题,并通过数据找到答案。 我们先来看看作者眼中的“魔鬼经济学”是什么,再选一个贴近我们生活的例子进行阐述。 01 魔鬼经济学 中心思想:假如道德代表人类对世界运转方式的期…...

2024.7.7总结
今天是惊心动魄的一天,记录一下吧! 昨天晚上害怕早上闹铃响了听不到,担心有意外出现,错过回家的车票,于是便在晚上设置了3个闹铃,6:50,7:00,7:05然后也关了静音。没想到,早上按照正…...
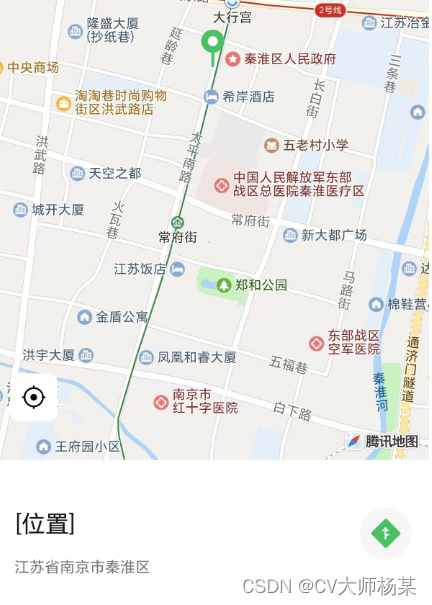
uniapp做小程序内打开地图展示位置信息
使用场景:项目中需要通过位置信息打开地图查看当前位置信息在地图那个位置,每个酒店有自己的经纬度和详细地址,点击地图按钮打开内置地图如图 方法如下: <view class"dttu" click"openMap(info.locationY,info.…...

leetcode 283.移动零
leetcode 283.移动零 自己刷题并且进行记录一下 题解 c class Solution { public:void moveZeroes(vector<int>& nums) {int count 0;for (int i 0; i < nums.size(); i) {if(nums[i] ! 0) {nums[count] nums[i];if (count !i) {nums[i] 0;}count;}}} };...
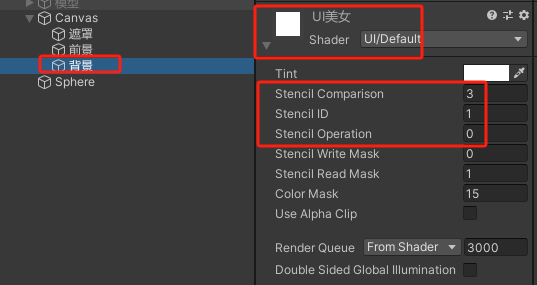
Unity | Shader基础知识(第十七集:学习Stencil并做出透视效果)
目录 一、前言 二、了解unity预制的材质 三、什么是Stencil 四、UGUI如何使用Stencil(无代码) 1.Canvas中Image使用Stencil制作透视效果 2.学习Stencil 3.分析透视效果的需求 五、模型如何使用Stencil 1.shader准备 2.渲染顺序 3.Stencil代码语…...
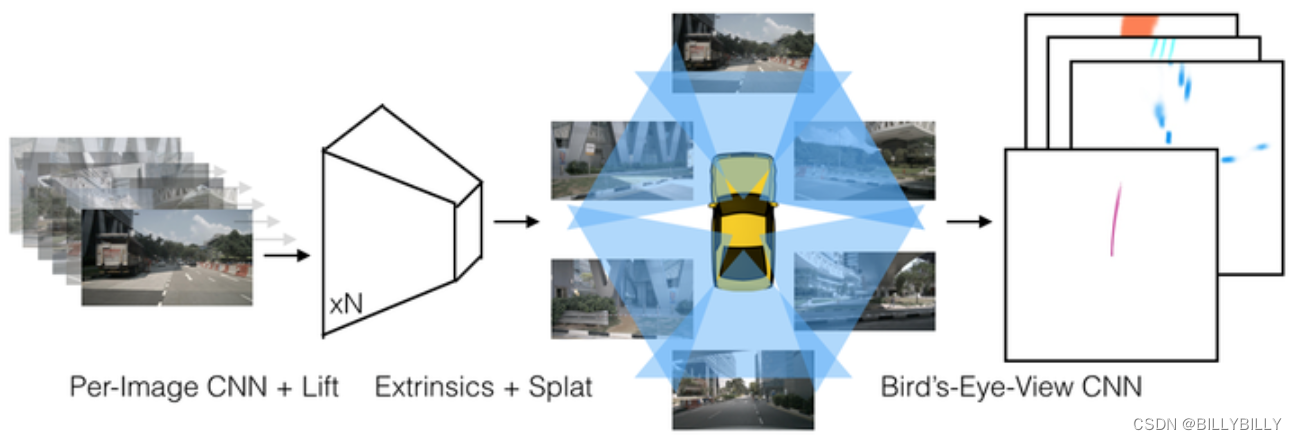
【3D->2D转换(1)】LSS(提升,投放,捕捉)
Lift, Splat, Shoot 这是一个端到端架构,直接从任意数量的摄像头数据提取给定图像场景的鸟瞰图表示。将每个图像分别“提升(lift)”到每个摄像头的视锥(frustum),然后将所有视锥“投放(splat&a…...

MyBatis 框架核心及面试知识要点
1、什么是 MyBatis? MyBatis 是一款优秀的支持自定义 SQL 查询、存储过程和高级映射的持久层框架,消除了 几乎所有的 JDBC 代码和参数的手动设置以及结果集的检索 。 MyBatis 可以使用 XML,或注解进 行配置和映射,MyBatis 通过将参数映射到配置的 SOL,形…...

《linux系统内核设计与实现》-实现最简单的字符设备驱动
开发linux内核驱动需要以下4个步骤: 1 编写hello驱动代码 驱动代码如下 helloDev.c,这是一个最小、最简单的驱动,去掉了其他的不相干代码,尽量让大家能了解驱动本身。 #include <linux/module.h> #include <linux/mod…...
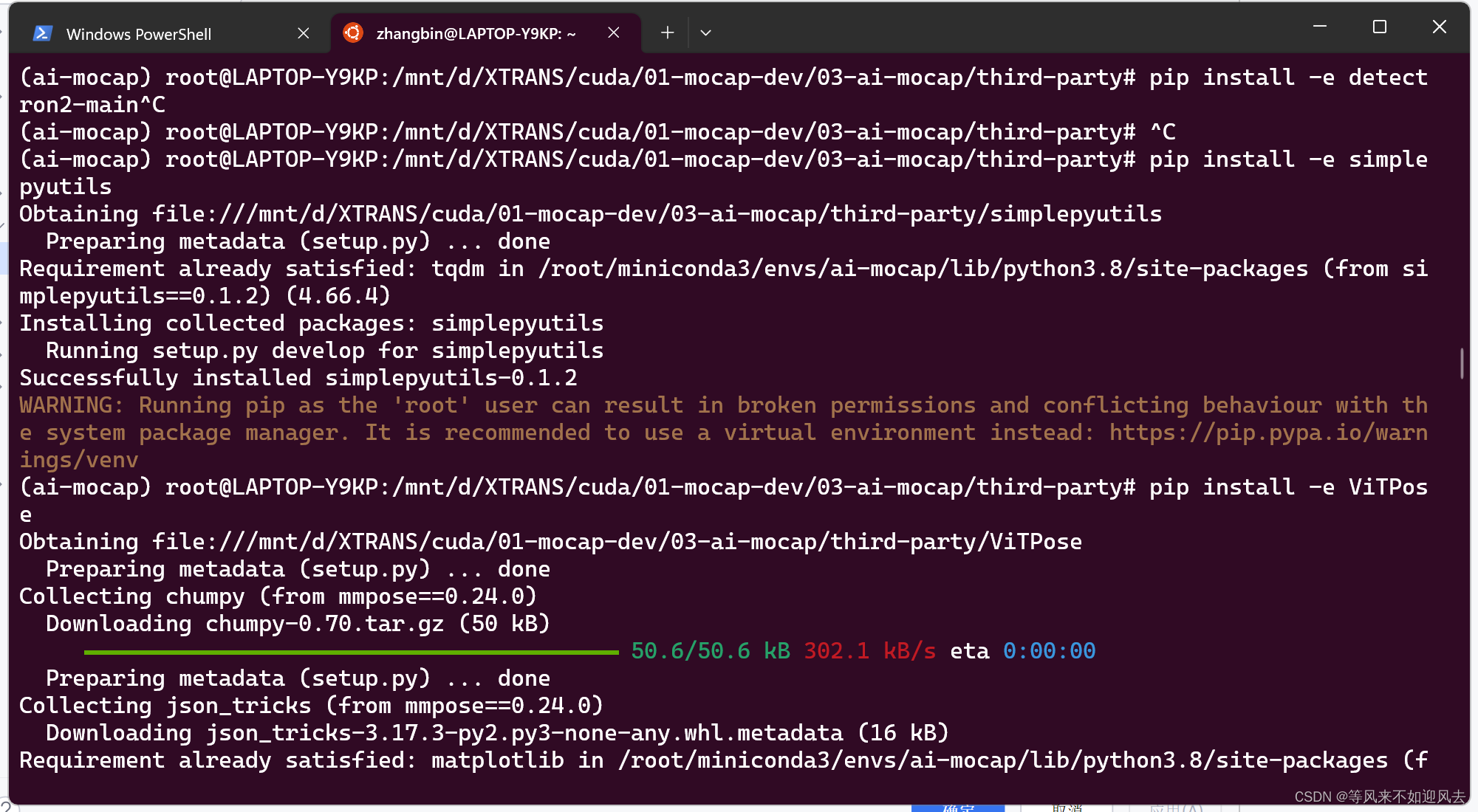
【MotionCap】pycharm 远程在wsl2 ubuntu20.04中root的miniconda3环境
pycharm wsl2 链接到pycharmsbin 都能看到内容,/root 下内容赋予了zhangbin 所有,pycharm还是看不到/root 下内容。sudo 安装了miniconda3 引发了这些问题 由于是在 root 用户安装的miniconda3 所以安装路径在/root/miniconda3 里 这导致了环境也是root用户的,会触发告警 WA…...

[BJDCTF 2nd]简单注入
sqlsqlsqlsqlsql又来喽 过滤了单双引号,等于符号,还有select等,但是这里没有二次注入 。扫描发现hint.txt 看出题人的意思是,得到密码即可获得flag。 select * from users where username$_POST["username"] and passw…...

java项目的一些功能(完善登录功能、注册接口参数校验、完善分页查询、完善日期格式、更新文章分类和添加文章分类的分组校验、自定义校验、文件上传 )
目录 完善登录功能 注册接口参数校验 完善分页查询 完善日期格式 更新文章分类和添加文章分类的分组校验 编辑 自定义校验 文件上传 完善登录功能 对前端传过来的明文密码进行md5加密处理 password DigestUtils.md5DigestAsHex(password.getBytes()); 这样既可 注…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...
