FFT剖析
快速傅里叶变换 (fast Fourier transform)
xn={x0,x1,…xn-1} (num:N)
旋转因子系数:
d=2pik/N
旋转因子
wk(n)=(cos(dn)+isin(dn)) n=[0,N-1]
y(k)= sum(x(n)wk(n),0,N-1)
y(k)={y(0),y(1),…y(N-1)} 傅里叶级数
x(n)wk(n)的级数是:
1.d=2pik/N 这个系数决定转动圈数,不懂看第二个再说
2.y(k)=x(0)wk(0)+x(1)wk(2)+…+x(n-1)wk(n-1)
旋转因子:cos(t)+isin(t)
t=2pikn/N
T=2pi就是一圈,那么可以得出步进量:2pi*k/N, 圈数:k
在一圈中:wk(n)的单位圆上t<=pi/2,是他的展开区 t<=pi是他的对称区
#include <bits/stdc++.h>
#define fu(x , y , z) for(int x = y ; x <= z ; x ++)
#define fd(x , y , z) for(int x = y ; x >= z ; x --)
#define LL long long
using namespace std;
const int N = 4e6 + 5;
const double pi = acos (-1.0);
struct node {double x , y;
} a[N] , b[N];
int n , m , len = 1 , r[N] , l;
node operator + (node a, node b) { return (node){a.x + b.x , a.y + b.y};}
node operator - (node a, node b) { return (node){a.x - b.x , a.y - b.y};}
node operator * (node a, node b) { return (node){a.x * b.x - a.y * b.y , a.x * b.y + a.y * b.x};}
int read () {int val = 0 , fu = 1;char ch = getchar ();while (ch < '0' || ch > '9') {if (ch == '-') fu = -1;ch = getchar ();}while (ch >= '0' && ch <= '9') {val = val * 10 + (ch - '0');ch = getchar ();}return val * fu;
}
void fft (node *A , int inv) {for (int i = 0 ; i < len ; i ++)if (i < r[i]) swap (A[i] , A[r[i]]);for (int mid = 1 ; mid < len ; mid <<= 1) { //mid={1,2,4,8,16,32,64,...}node wn = (node){cos (1.0 * pi / mid) , inv * sin (1.0 * pi / mid)};for (int R = mid << 1 , j = 0 ; j < len ; j += R) {node w = (node){1 , 0};for (int k = 0 ; k < mid ; k ++ , w = w * wn) {node x = A[j + k] , y = w * A[j + mid + k];A[j + k] = x + y;A[j + mid + k] = x - y;}}}
}
int main () {n = read () , m = read ();fu (i , 0 , n) a[i].x = read ();fu (i , 0 , m) b[i].x = read ();while (len <= n + m) len <<= 1 , l ++;for (int i = 0 ; i < len ; i ++)r[i] = (r[i >> 1] >> 1) | ((i & 1) << (l - 1));fft (a , 1);fft (b , 1);fu (i , 0 , len) a[i] = a[i] * b[i];fft (a , -1);// for (int i = 0 ; i <= n + m ; i ++) cout << a[i].x << " " << a[i].y << "\n";fu (i , 0 , n + m) printf ("%d " , (int)(a[i].x / len + 0.5));return 0;
}计算2^n的逆排长度:2的6次方:64=0b100-0000;逆排长度0b11-1111
while (len <= n + m) len <<= 1 , l ++;
产生逆排:0,32,
for (int i = 0 ; i < len ; i ++)
r[i] = (r[i >> 1] >> 1) | ((i & 1) << (l - 1));
逆排交换数据
for (int i = 0 ; i < len ; i ++)
if (i < r[i])
swap (A[i] , A[r[i]]);
#include <bits/stdc++.h>
#define fu(x , y , z) for(int x = y ; x <= z ; x ++)
using namespace std;
const int N = 4e6 + 5;
const double pi = acos (-1.0);
int n , m1 , m2 , rev[N];
complex<double> a[N] , b[N];
void fft (complex<double> *a , int type) {fu (i , 0 , n - 1) if (i < rev[i]) swap (a[i] , a[rev[i]]);for (int j = 1 ; j < n ; j <<= 1) {complex<double> W(cos (pi / j) , sin (pi / j) * type);for (int k = 0 ; k < n ; k += (j << 1)) {complex<double> w(1.0 , 0.0);fu (i , 0 , j - 1) {complex<double> ye , yo;ye = a[i + k] , yo = a[i + j + k] * w;a[i + k] = ye + yo;a[i + k] = ye + yo;a[i + j + k] = ye - yo;w *= W;}}}
}
int main () {scanf ("%d%d" , &m1 , &m2);fu (i , 0 , m1) cin >> a[i];fu (i , 0 , m2) cin >> b[i];n = m1 + m2;int t = 0;while (n >= (1 << t)) t ++;n = (1 << t);fu (i , 0 , n - 1) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) ? (n >> 1) : 0);fft (a , 1) , fft (b , 1);fu (i , 0 , n) a[i] *= b[i];fft (a , -1);fu (i , 0 , m1 + m2) printf ("%d " , (int)(a[i].real() / (double)n + 0.5));return 0;
}f0=(a0,a1,…an-2)
f1=(a1,a3,…an-1)
f(wnk)=f0(wnk/2)+wnkf1(wkn/2)
f(wn(k+n/2)=f0(wnk/2)-wnkf1(wkn/2)
#include<cstdio>2 #include<iostream>3 #include<cmath>4 #include<cstring>5 #include<algorithm>6 #include<cstdlib>7 using namespace std;8 const int mod=1e9+7;9 const double pi=acos(-1);
10 struct cn
11 {
12 double x,y;
13 cn (double x=0,double y=0):x(x),y(y) {}
14 }a[300005],b[300005],c[300005];
15 cn operator + (const cn &a,const cn &b) {return cn(a.x+b.x,a.y+b.y);}
16 cn operator - (const cn &a,const cn &b) {return cn(a.x-b.x,a.y-b.y);}
17 cn operator * (const cn &a,const cn &b) {return cn(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}
18 void fft(cn a[],int n,int l,int f)
19 {
20 int rev[n+5];
21 rev[0]=0;
22 for (int i=1; i<n; i++){
23 rev[i]=(rev[i>>1]>>1)|((i&1)<<l-1);
24 if (i<rev[i]) swap(a[i],a[rev[i]]);
25 }
26 for (int i=1; i<n; i<<=1){
27 cn wi(cos(pi/i),f*sin(pi/i));
28 for (int j=0; j<n; j+=i*2){
29 cn w(1,0);
30 for (int k=0; k<i; k++){
31 cn x=a[j+k],y=w*a[j+k+i];
32 a[j+k]=x+y;
33 a[j+k+i]=x-y;
34 w=w*wi;
35 }
36 }
37 }
38 if (f==-1)
39 for (int i=0; i<n; i++){
40 a[i].x/=n; a[i].y/=n;
41 }
42 }
43 int main()
44 {
45 int n,m;
46 scanf("%d%d",&n,&m); n++; m++;
47 for (int i=0; i<n; i++) scanf("%lf",&a[i].x);
48 for (int i=0; i<m; i++) scanf("%lf",&b[i].x);
49 int l=0,N=1;
50 while (N<n+m-1) N<<=1,l++;
51 fft(a,N,l,1);
52 fft(b,N,l,1);
53 for (int i=0; i<N; i++) c[i]=a[i]*b[i];
54 fft(c,N,l,-1);
55 for (int i=0; i<n+m-1; i++) printf("%d ",(int)(c[i].x+0.5));
56 return 0;
57 }相关文章:

FFT剖析
快速傅里叶变换 (fast Fourier transform) xn{x0,x1,…xn-1} (num:N) 旋转因子系数: d2pik/N 旋转因子 wk(n)(cos(dn)isin(dn)) n[0,N-1] y(k) sum(x(n)wk(n),0,N-1) y(k){y(0),y(1),…y(N-1)} 傅里叶级数 x(n)wk(n)的级数是: 1.d2pik/N 这个系数决…...

git clone报错RPC failed; curl 92 HTTP/2 stream 7 was not closed cleanly
问题描述 git clone github上的项目报错: RPC failed; curl 92 HTTP/2 stream 7 was not closed cleanly: CANCEL (err 8) 4796 bytes of body are still expected fetch-pack: unexpected disconnect while reading sideband packet early EOF fetch-pack: invalid index-pac…...

Apispec,一个用于生成 OpenAPI(Swagger)规范的 Python 库
目录 01什么是 Apispec? 为什么选择 Apispec? 安装与配置 02Apispec 的基本用法 生成简单的 API 文档 1、创建 Apispec 实例 2、定义 API 路由和视图 3、添加路径到 Apispec 集成 Flask 和 Apispec 1、安装…...

SpringBoot 自定义异常返回数据格式
Spring Boot 默认异常处理 当我们用 spring boot 开发接口是,当遇到异常时返回的数据格式是如下形式的 {"timestamp": "2024-07-06T02:48:55.79100:00","status": 404,"error": "Not Found","path":…...
【xinference】(15):在compshare上,使用docker-compose运行xinference和chatgpt-web项目,配置成功!!!
视频演示 【xinference】(15):在compshare上,使用docker-compose运行xinference和chatgpt-web项目,配置成功!!! 1,安装docker方法: #!/bin/shdistribution$(…...

【Unity 3D角色移动】
【Unity 3D角色移动】 在Unity 3D中实现角色移动通常涉及到几个关键步骤,包括设置角色的物理属性、处理输入、更新角色的位置以及动画同步。下面是实现基本3D角色移动的步骤和示例代码: 步骤1:设置角色的物理属性 角色通常使用Character Co…...

个人视角,社会影响力:自媒体的魅力所在
随着数字化时代的到来,自媒体正成为信息传播领域的一场革命。个人视角与社会影响力的结合,赋予了自媒体独特的魅力。在传统媒体受限制的同时,自媒体为每个人提供了表达自己观点和思想的自由。个体的真实视角使得自媒体在信息传播中发挥着重要…...

算法训练营day70
题目1:108. 冗余连接 (kamacoder.com) #include<iostream> #include<vector>using namespace std;int n; vector<int> father(10001, 0);void init() {for(int i 1;i < n;i) father[i] i; }int find(int u) {return u father[u] ? u : fa…...

EtherCAT转Profinet网关配置说明第二讲:上位机软件配置
EtherCAT协议转Profinet协议网关模块(XD-ECPNS20),不仅可以实现数据之间的通信,还可以实现不同系统之间的数据共享。EtherCAT协议转Profinet协议网关模块(XD-ECPNS20)具有高速传输的特点,因此通…...

日志自动分析-Web---360星图GoaccessALBAnolog
目录 1、Web-360星图(IIS/Apache/Nginx) 2、Web-GoAccess (任何自定义日志格式字符串) 源码及使用手册 安装goaccess 使用 输出 3-Web-自写脚本(任何自定义日志格式字符串) 4、Web-机器语言analog(任何自定义日…...

【面试八股文】java基础知识
引言 本文是java面试时的一些常见知识点总结归纳和一些拓展,笔者在学习这些内容时,特地整理记录下来,以供大家学习共勉。 一、数据类型 1.1 为什么要设计封装类,Integer和int区别是什么? 使用封装类的目的 对象化:…...

ssrf结合redis未授权getshell
目录 漏洞介绍 SSRF Redis未授权 利用原理 环境搭建 利用过程 rockylinux cron计划任务反弹shell 写公钥免密登录 ubuntu 写公钥免密登录 漏洞介绍 SSRF SSRF(server side request forgrey)服务端请求伪造,因后端未过滤用户输入&…...

魔法自如:精通 IPython %automagic 命令的切换艺术
魔法自如:精通 IPython %automagic 命令的切换艺术 在 IPython 的神奇世界里,魔术命令是其强大交互功能的核心。这些以 % 或 %% 开头的命令,能够执行一系列特殊的操作,从而增强用户的编程体验。但是,你是否知道&#…...

基于CentOS Stream 9平台搭建MinIO以及开机自启
1. 官网 https://min.io/download?licenseagpl&platformlinux 1.1 下载二进制包 指定目录下载 cd /opt/coisini/ wget https://dl.min.io/server/minio/release/linux-amd64/minio1.2 文件赋权 chmod x /opt/coisini/minio1.3 创建Minio存储数据目录: mkdi…...

shell-awk语法整理
shell-awk语法整理 前言基本语法内置变量1. $02. NF3. NR4. FS5. RS6. OFS7. ORS8. FILENAME9. FNR10. ARGV11. ENVIRON12. IGNORECASE13. RSTART 和 RLENGTH示例解释 内置函数循环语句(后面的;可不加)条件语句高级特性示例 特殊模式BEGINEND组合示例BEG…...

关于忠诚:忠于自己的良知、理想、信念
关于忠诚: 当我们面对公司、上司、爱人、恋人、合作伙伴还是某件事,会纠结离开还是留下,这里我们要深知忠诚的定义,我们不是忠诚于某个人、某件事、或者某个机构,而是忠诚于自己的良知,忠诚于自己的理想和…...

探索Linux:开源世界的无限可能
Linux是一款开源操作系统,它的起源可以追溯到上世纪90年代初。这个故事始于一个名叫Linus Torvalds的芬兰大学生,他在1983年开始编写一个用于个人电脑的操作系统内核。在他的努力下,Linux逐渐发展成为一个稳定而强大的操作系统。 然而&#…...
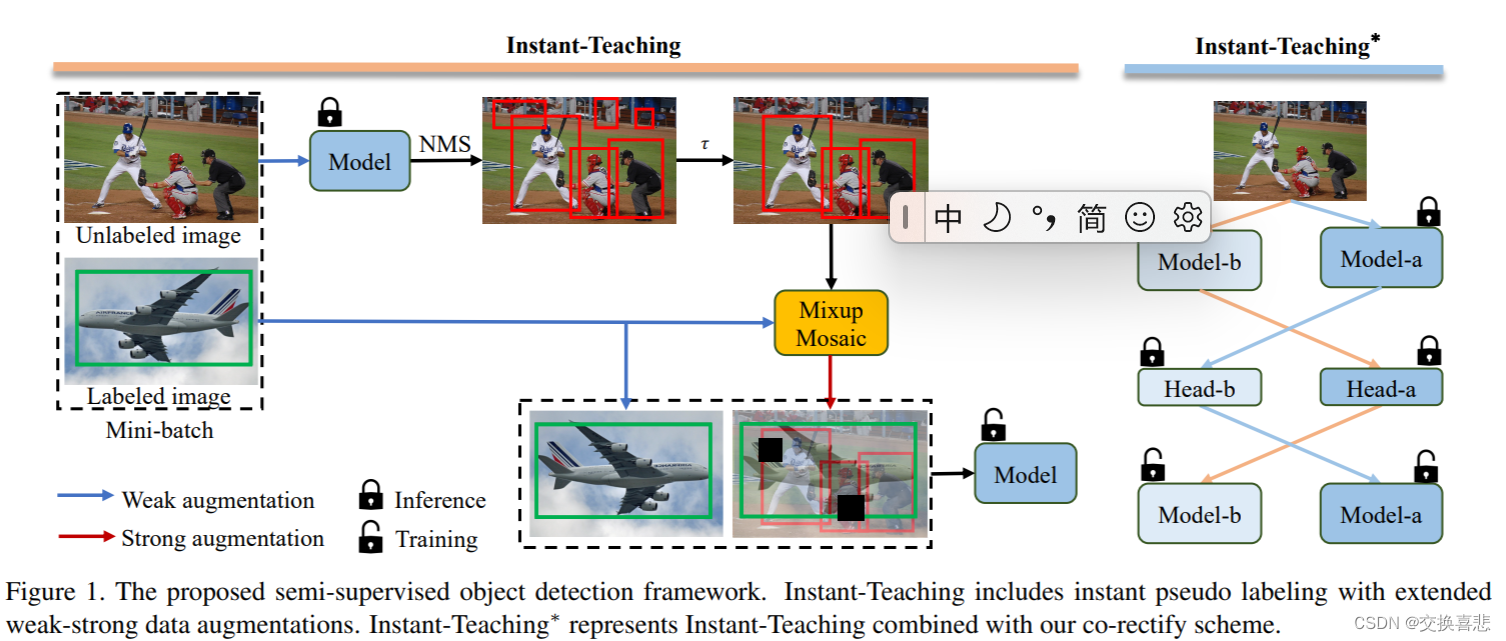
深度学习之半监督学习:一文梳理目标检测中的半监督学习策略
什么是半监督目标检测? 传统机器学习根据训练数据集中的标注情况,有着不同的场景,主要包括:监督学习、弱监督学习、弱半监督学习、半监督学习。由于目标检测任务的特殊性,在介绍半监督目标检测方法之前,我…...
Hive 高可用分布式部署详细步骤
目录 系统版本说明 hive安装包下载及解压 上传mysql-connector-java的jar包 配置环境变量 进入conf配置文件中,将文件重命名 在hadoop集群上创建文件夹 创建本地目录 修改hive-site.xml文件 同步到其他的节点服务器 修改node02中的配置 hive-site.xml 修改…...

ubuntu下运行程序时提示缺库问题的有效解决方法
目录 一、问题现象二、解决方式三、总结 一、问题现象 当我们平时在ubuntu上运行一个程序时时长会遇到如下情况,含义为本机缺少执行程序需要的库 这时候我们可能会根据缺少的库使用apt install 库名的模糊名字 进行安装,然后再去运行,此时可…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
