众所周知沃尔玛1P是怎么运营?
沃尔玛的1P模式,即第一方供应商模式,是其独特的采购策略。在这种模式下,供应商先将商品卖给沃尔玛,由沃尔玛负责库存管理和销售。沃尔玛通过强大的采购和物流能力控制库存,确保商品品质,为客户提供更加优质的购物体验。

在1P模式下,沃尔玛承担了库存管理的风险,而供应商则可以借助沃尔玛的销售渠道,扩大市场份额,提升品牌价值。此模式通常适用于市场需求稳定、库存周转快的商品,如食品、日用品等。
对于想要加入沃尔玛1P模式的供应商,以下是一些关键步骤:
1. 在沃尔玛官网注册账号,并提交公司资质、产品信息和品牌授权等文件,以确保合法性和商品质量。
2. 通过认证后,按照沃尔玛的规范上架商品,包括商品描述、图片和价格。同时,供应商需要关注库存情况,确保充足和及时补货。
3. 制定销售策略和推广计划,利用沃尔玛的营销工具如促销、广告投放和数据分析来提高商品的曝光度和销售额。此外,供应商还可以通过社交媒体和搜索引擎优化等外部推广方式来吸引潜在客户。
4. 在订单处理与售后服务方面,供应商需要及时处理订单,按时发货,并提供优质的售后服务,如退换货和咨询解答,以维护客户满意度和品牌形象。

值得注意的是,沃尔玛对1P供应商的产品质量、价格竞争力以及市场口碑等方面有着较高的要求。因此,供应商需要不断提升自身实力,以满足沃尔玛的采购标准。总的来说,沃尔玛的1P模式为供应商提供了一个借助其强大销售渠道扩大市场份额的机会,但同时也要求供应商具备一定的实力和信誉。
相关文章:

众所周知沃尔玛1P是怎么运营?
沃尔玛的1P模式,即第一方供应商模式,是其独特的采购策略。在这种模式下,供应商先将商品卖给沃尔玛,由沃尔玛负责库存管理和销售。沃尔玛通过强大的采购和物流能力控制库存,确保商品品质,为客户提供更加…...
【Linux】静态库的制作和使用详解
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...

2.贪心算法.基础
2.贪心算法.基础 基础知识题目1.分发饼干2.摆动序列2.1.思路二:动态规划法 3.最大子序和4.买股票的最佳时机24.1.思路二:动态规划法4.2.买股票的最佳时机 5.跳跃游戏5.1.跳跃游戏2 6.K次取反后最大化的数组和7.加油站8.分发糖果 总结 基础知识 什么是贪…...

用Python轻松转换PDF为CSV
数据的可访问性和可操作性是数据管理的核心要素。PDF格式因其跨平台兼容性和版面固定性,在文档分享和打印方面表现出色,尤其适用于报表、调查结果等数据的存储。然而,PDF的非结构化特性限制了其在数据分析领域的应用。相比之下,CS…...

关于微信支付-商户平台:查询订单提示“查询失败:操作失败,请稍候重试”的分析
目录 引子 分析 应对 小结 引子 在开发和实施微信 JSAPI 支付的应用后,我们遇到了一些问题,订单的状态更新不正常,当然我们首先需要从自身寻找原因和完善解决问题的办法和方案。在支付的过程中,客户会给我们一些反馈…...

掌握【Python异常处理】:打造健壮代码的现代编程指南
目录 编辑 1. 什么是异常? 知识点 示例 小李的理解 2. 常见的内置异常类型 知识点 示例 小李的理解 3. 异常机制的意义 知识点 示例 小李的理解 4. 如何处理异常 知识点 示例 小李的理解 5. 抛出异常 知识点 示例 小李的理解 6. Python内置…...

STM32点灯闪烁
stm32c8t6引脚图 开发板引脚图 GPIO端口的每个位可以由软件分别配置成 多种模式。 ─ 输入浮空 ─ 输入上拉 ─ 输入下拉 ─ 模拟输入 ─ 开漏输出 ─ 推挽式输出 ─ 推挽式复用功能 ─ 开漏复用功能 配置GPIO端口步骤:开启时钟->使用结构体设置输出模式…...

Java-01-源码篇-04集合-05-SortedMap NavigableMap TreeMap
目录 一,SortedMap 二,NavigableMap 三,TreeMap 3.1 TreeMap 继承结构 3.2 TreeMap 属性 3.3 TreeMap 构造器 3.4 TreeMap 内部类 3.4.1 Values 3.4.2 KeySet 3.4.3 EntrySet 3.4.5 相关集合迭代器 3.4.5.1 PrivateEntryIterato…...
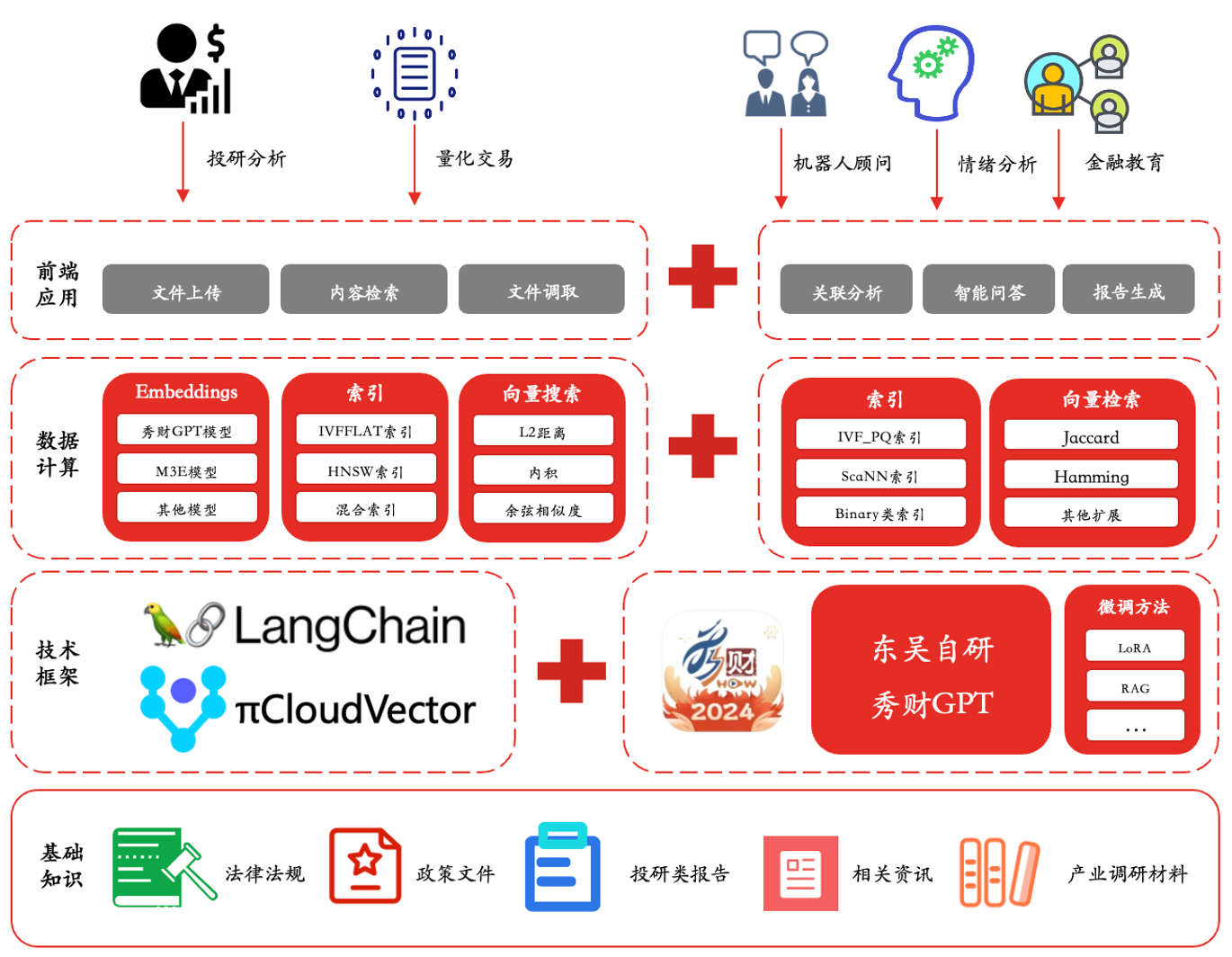
拥抱 AGI:PieDataCS 引领云原生数据计算系统新范式
自2023年后,人工智能技术进入了一个更为成熟和广泛应用的阶段,人工通用智能(AGI)这一概念也成为了科技界和产业界热议的焦点。本文将结合 AGI 时代背景,从架构设计到落地实践,详细介绍拓数派云原生数据计算…...

开放式耳机哪个品牌好?开放式耳机推荐
开放式耳机因其独特的设计,提供了更自然的听音体验和更好的环境声音感知,尤其适合长时间佩戴和户外运动使用,下面来推荐几款表现出色的开放式耳机: 悠律ringbuds pro凝声环(499元):凭借时尚潮流…...
kubernetes dashboard安装
1.查看符合自己版本的kubernetes Dashboard 比如我使用的是1.23.0版本 https://github.com/kubernetes/dashboard/releases?page5 对应版本 kubectl apply -f https://raw.githubusercontent.com/kubernetes/dashboard/v2.5.1/aio/deploy/recommended.yaml修改对应的yaml,…...

【MySQL】3.表的操作
表的操作 一.创建表二.查看表三.修改表四.删除表 一.创建表 create table [if not exists] tb_name( field1 datatype comment 说明, field2 datatype, field3 datatype) charsetutf8 collateutf8_gerenal_ci engineInnoDB//表的编码集,校验集如果不指定ÿ…...

十一、作业
1.从大到小输出 写代码将三个整数数按从大到小输出。 void Swap(int* px, int* py) {int tmp *px;*px *py;*py tmp;} int main() {int a 0;int b 0;int c 0;scanf("%d %d %d", &a, &b, &c);int n 0;if (a<b){Swap(&a, &b);}if (a &l…...

关于C#在WPF中如何使用“抽屉”控件
关于C#在WPF中如何使用“抽屉”控件 1.前提准备2.XAML代码3.对应的C#代码4.显示效果 1.前提准备 需要引用MaterialDesign控件库,关于如何引用,请参照文章——关于C#如何引用MaterialDesign控件库 2.XAML代码 <Window x:Class"MaterialDesign_…...

运维Tips | Ubuntu 24.04 安装配置 xrdp 远程桌面服务
[ 知识是人生的灯塔,只有不断学习,才能照亮前行的道路 ] Ubuntu 24.04 Desktop 安装配置 xrdp 远程桌面服务 描述:Xrdp是一个微软远程桌面协议(RDP)的开源实现,它允许我们通过图形界面控制远程系统。这里使…...

ExcelVBA运用Excel的【条件格式】(二)
ExcelVBA运用Excel的【条件格式】(二) 前面知识点回顾 1. 访问 FormatConditions 集合 Range.FormatConditions 2. 添加条件格式 FormatConditions.Add 方法 语法 表达式。添加 (类型、 运算符、 Expression1、 Expression2) 3. 修改或删除条件…...

肠道和大脑中犬尿氨酸代谢途径的紊乱
新出现的证据表明,肠道微生物群可能与宿主大脑相互作用,并在神经精神疾病的发病机制中发挥关键作用。然而,抑郁症中微生物-肠-脑轴相互作用的潜在机制仍不清楚。在这项研究中,建立了慢性约束应激 (CRS) 的小鼠模型,以研…...

vue通过后台返回的数字显示不同的文字内容,多个内容用、隔开
后台返回的数据 显示效果: html: <el-table-columnalign"center"label"使用过的小程序"width"124"v-if"activeTab 0"><template #default"scope"><divv-for"(item, index) in s…...

Flume工具详解
Flume是一个由Apache提供的开源日志收集系统,最初由Cloudera贡献。它以其高可用性、高可靠性和分布式特性而著称,被广泛应用于海量日志的采集、聚合和传输。以下是对Flume工具的详细解析: 一、概述 功能定位:Flume主要用于收集、…...

vulhub-activemq(CVE-2016-3088)
在 Apache ActiveMQ 5.12.x~5.13.x 版本中,默认关闭了 fileserver 这个应用(不过,可以在conf/jetty.xml 中开启);在 5.14.0 版本后,彻底删除了 fileserver 应用。【所以在渗透测试过程中要确定好 ActiveMQ …...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
