kubernetes dashboard安装
1.查看符合自己版本的kubernetes Dashboard
比如我使用的是1.23.0版本
https://github.com/kubernetes/dashboard/releases?page=5
对应版本
kubectl apply -f https://raw.githubusercontent.com/kubernetes/dashboard/v2.5.1/aio/deploy/recommended.yaml
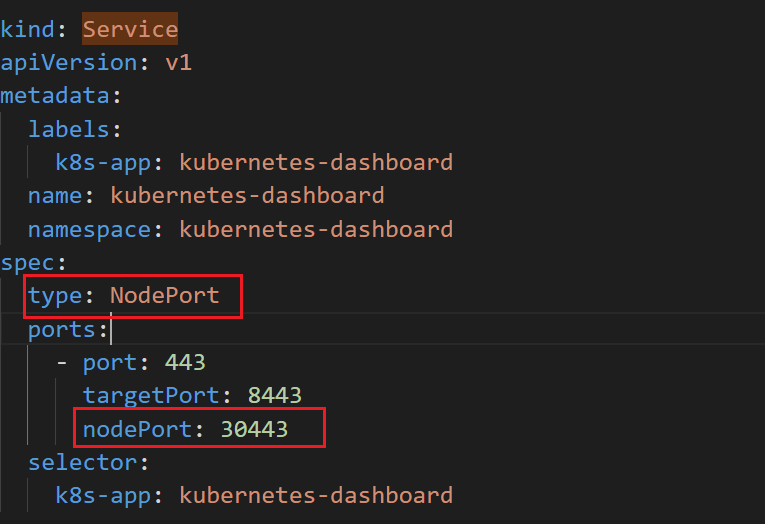
修改对应的yaml, 在kind: Service节点的spec节点下添加 type: NodePort ,并暴露端口30443
2.不是私密连接问题
页面出现安全验证
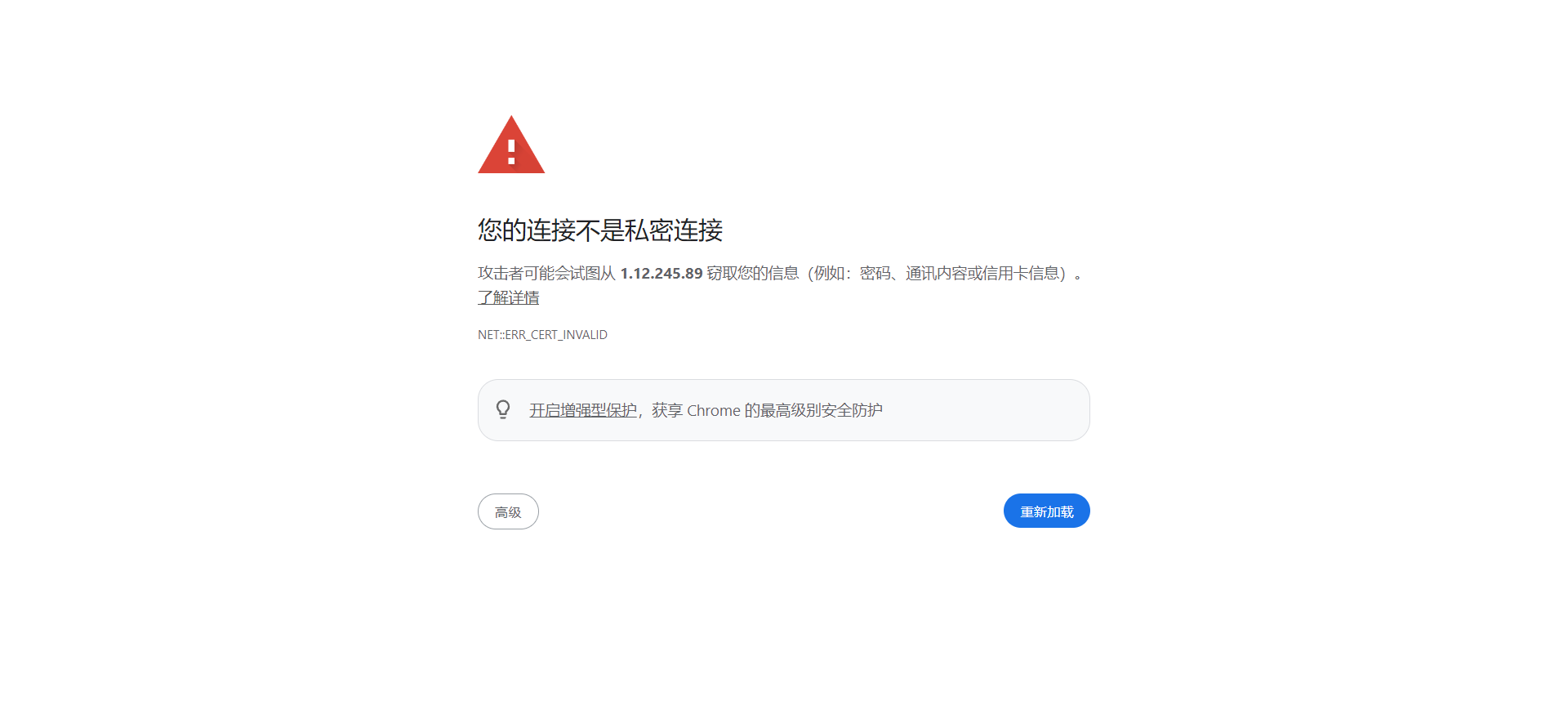
直接键盘输入 ：thisisunsafe
3.创建token
创建一个具有必要权限的服务账户。使用admin-user.yaml 创建一个名为 admin-user 的服务账户：
yamlCopyapiVersion: v1
kind: ServiceAccount
metadata:name: admin-usernamespace: kubernetes-dashboard---apiVersion: rbac.authorization.k8s.io/v1
kind: ClusterRoleBinding
metadata:name: admin-user
roleRef:apiGroup: rbac.authorization.k8s.iokind: ClusterRolename: cluster-admin
subjects:
- kind: ServiceAccountname: admin-usernamespace: kubernetes-dashboard
运行
kubectl apply -f admin-user.yaml
获取 token： 对于 Kubernetes v1.24 及以上版本：
kubectl create token admin-user -n kubernetes-dashboard
对于较早版本的 Kubernetes：
kubectl -n kubernetes-dashboard describe secret $(kubectl -n kubernetes-dashboard get secret | grep admin-user | awk '{print $1}')
相关文章：
kubernetes dashboard安装
1.查看符合自己版本的kubernetes Dashboard 比如我使用的是1.23.0版本 https://github.com/kubernetes/dashboard/releases?page5 对应版本 kubectl apply -f https://raw.githubusercontent.com/kubernetes/dashboard/v2.5.1/aio/deploy/recommended.yaml修改对应的yaml,…...
【MySQL】3.表的操作
表的操作 一.创建表二.查看表三.修改表四.删除表 一.创建表 create table [if not exists] tb_name( field1 datatype comment 说明, field2 datatype, field3 datatype) charsetutf8 collateutf8_gerenal_ci engineInnoDB//表的编码集，校验集如果不指定ÿ…...
十一、作业
1.从大到小输出 写代码将三个整数数按从大到小输出。 void Swap(int* px, int* py) {int tmp *px;*px *py;*py tmp;} int main() {int a 0;int b 0;int c 0;scanf("%d %d %d", &a, &b, &c);int n 0;if (a<b){Swap(&a, &b);}if (a &l…...
关于C#在WPF中如何使用“抽屉”控件
关于C#在WPF中如何使用“抽屉”控件 1.前提准备2.XAML代码3.对应的C#代码4.显示效果 1.前提准备 需要引用MaterialDesign控件库，关于如何引用，请参照文章——关于C#如何引用MaterialDesign控件库 2.XAML代码 <Window x:Class"MaterialDesign_…...
运维Tips | Ubuntu 24.04 安装配置 xrdp 远程桌面服务
[ 知识是人生的灯塔，只有不断学习，才能照亮前行的道路 ] Ubuntu 24.04 Desktop 安装配置 xrdp 远程桌面服务 描述：Xrdp是一个微软远程桌面协议（RDP）的开源实现，它允许我们通过图形界面控制远程系统。这里使…...
ExcelVBA运用Excel的【条件格式】（二）
ExcelVBA运用Excel的【条件格式】（二） 前面知识点回顾 1. 访问 FormatConditions 集合 Range.FormatConditions 2. 添加条件格式 FormatConditions.Add 方法 语法 表达式。添加 (类型、 运算符、 Expression1、 Expression2) 3. 修改或删除条件…...
肠道和大脑中犬尿氨酸代谢途径的紊乱
新出现的证据表明，肠道微生物群可能与宿主大脑相互作用，并在神经精神疾病的发病机制中发挥关键作用。然而，抑郁症中微生物-肠-脑轴相互作用的潜在机制仍不清楚。在这项研究中，建立了慢性约束应激 (CRS) 的小鼠模型，以研…...
vue通过后台返回的数字显示不同的文字内容，多个内容用、隔开
后台返回的数据 显示效果： html： <el-table-columnalign"center"label"使用过的小程序"width"124"v-if"activeTab 0"><template #default"scope"><divv-for"(item, index) in s…...
Flume工具详解
Flume是一个由Apache提供的开源日志收集系统，最初由Cloudera贡献。它以其高可用性、高可靠性和分布式特性而著称，被广泛应用于海量日志的采集、聚合和传输。以下是对Flume工具的详细解析： 一、概述 功能定位：Flume主要用于收集、…...
vulhub-activemq(CVE-2016-3088)
在 Apache ActiveMQ 5.12.x~5.13.x 版本中，默认关闭了 fileserver 这个应用（不过，可以在conf/jetty.xml 中开启）；在 5.14.0 版本后，彻底删除了 fileserver 应用。【所以在渗透测试过程中要确定好 ActiveMQ …...
上海市计算机学会竞赛平台2024年6月月赛丙组超级奇数
题目描述 如果一个十进制数的所有数字都是奇数，则称之为超级奇数，例如 35733573 就是一个超级奇数，而 3141531415 不是。按照从小到大排序，前几名的超级奇数为 1,3,5,7,9,11,13,15,17,⋯1,3,5,7,9,11,13,15,17,⋯ 给定一个超级…...
速盾：cdn业务优化
CDN（Content Delivery Network）是一种基于互联网的分布式网络架构，旨在提供更快速、可靠的内容传输服务。它通过将内容分发至多个节点，使用户可以从离他们更近的节点获取内容，从而提高访问速度和用户体验。 然而&…...
重生奇迹mu的地图名
地图之一：勇者大陆 勇者大陆地处奇迹大陆中央。终年阴雨连绵，气候潮湿闷热。植物由充满黑暗阴森气氛的草地所构成。这里的NPC数量是所有地图中最多的。因为地步交通要冲，所以也是玩家聚集最多的地方。 这里是剑士、魔法师、魔剑士和圣导师初…...
【CSS】缩写属性gap
在CSS Grid Layout（网格布局）和Flexbox（弹性盒布局）中，gap 是一个缩写属性，用于同时设置行间隙（gutter）和列间隙（在Flexbox中通常称为“交叉轴间隙”）的大小。…...
Perl 语言开发（八）：子程序和模块
目录 1. 引言 2. 子程序的基本概念与用法 2.1 子程序的定义和调用 2.2 传递参数 2.3 返回值 2.4 上下文和返回值 3. 模块的基本概念与用法 3.1 模块的定义 3.2 使用模块 3.3 导出符号 3.4 模块的文件结构和命名 4. 实际应用中的子程序与模块 4.1 子程序参数验证与…...
自注意力机制和多头注意力机制区别
Ref：小白看得懂的 Transformer (图解) Ref：一文彻底搞懂 Transformer（图解手撕） 多头注意力机制（Multi-Head Attention）和自注意力机制（Self-Attention）是现代深度学习模型&#x…...
数据结构第14节 加权图
加权图是在图论中一种更为复杂的图结构，它扩展了无向图和有向图的概念，通过给图中的边附加一个数值来表示边的某种属性，如成本、距离、容量或相似度等。这个数值被称为边的“权重”。 定义 加权图可以被形式化地定义为一个三元组 ( G (V, …...
128陷阱（超详细）
int x 128;int y 128;int n 127;int m 127;Integer d Integer.valueOf(x);Integer g Integer.valueOf(y);Integer z Integer.valueOf(n);Integer v Integer.valueOf(m);System.out.println(d g);System.out.println(z v); 思考一下他的结果是什么？ 为什么…...
STM32自己从零开始实操08:STM32主控原理图
由于老师使用的各引脚分门别类的单片机原理图我没有找到，我使用是引脚按顺序摆放的，不方便一个模块一个模块截图展示，所以这部分使用老师的原理图。 一、电源 1.1电源的介绍 1.1.1数字电源和地（VDD和VSS） 数字电源…...
Ubuntu20.04配置TurtleBot3 Waffle Pi远程控制
这里写目录标题 0. 机器人配置1. Ubuntu20.04配置TurtleBot3 Waffle Pi远程控制1.1 TurtleBot3 Waffle Pi端配置1.2 PC端配置1.2.1 安装turtlebot3的环境配置1.2.2 创建项目并安装Turtlebot31.2.3 配置环境变量 1.3 PC端与TurtleBot3进行通信1.3.1 PC端与机器人端互PING和SSH连…...
【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现，玩家控制一个角色（龙）躲避障碍物（仙人掌和乌鸦）。以下是代码的详细介绍：…...
【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中，用户注册、登录、修改密码等操作，都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输，在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...
Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...
sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...
MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现（两者等价），用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例： 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...
初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...
MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 ：主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 ：确保数据的完整性，便于数据的查询和管理。 示例 ：在学生信息表中，学号可以作为主键ÿ…...
掌握 HTTP 请求：理解 cURL GET 语法
cURL 是一个强大的命令行工具，用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中，cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...
一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序，无论是测试应用程序、搜寻漏洞还是收集情报，它们都能提升工作流程。 FoxyProxy 代理管理工具，此扩展简化了使用代理（如 Burp…...
Java后端检查空条件查询
通过抛出运行异常：throw new RuntimeException("请输入查询条件！");BranchWarehouseServiceImpl.java // 查询试剂交易（入库/出库）记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...