数据结构第14节 加权图
加权图是在图论中一种更为复杂的图结构,它扩展了无向图和有向图的概念,通过给图中的边附加一个数值来表示边的某种属性,如成本、距离、容量或相似度等。这个数值被称为边的“权重”。
定义
加权图可以被形式化地定义为一个三元组 ( G = (V, E, W) ),其中:
- ( V ) 是顶点的集合。
- ( E ) 是边的集合,每条边连接 ( V ) 中的一对顶点。
- ( W ) 是一个函数,将每条边映射到一个实数上,即 ( W: E \rightarrow \mathbb{R} )。
分类
加权图可以根据边的方向进一步分类为:
- 加权无向图:图中的边没有方向,权重是对称的,即 ( W(u,v) = W(v,u) )。
- 加权有向图:图中的边有方向,权重可能不对称,即 ( W(u,v) ) 可能与 ( W(v,u) ) 不同。
权重的意义
在不同的应用场景中,权重可以有不同的含义:
- 在网络路由中,权重可能是网络链路的延迟或带宽。
- 在交通网络中,权重可能是道路的距离或通行时间。
- 在电子电路中,权重可能是电阻或电容值。
- 在社交网络中,权重可以表示人际关系的强度。
图的表示
加权图可以通过以下几种方式表示:
- 邻接矩阵:对于加权图,邻接矩阵中的非零元素表示边的权重。
- 邻接列表:对于每个顶点,列表中的每个元素除了包含邻接顶点的信息外,还包含边的权重。
常见算法
处理加权图的一些常见算法包括:
- 最短路径算法:如Dijkstra算法和Bellman-Ford算法,用于找到两点间具有最小权重和的路径。
- 最小生成树算法:如Prim算法和Kruskal算法,用于在加权连通图中找到一棵包含所有顶点的最小权重的树。
- 最大流算法:如Ford-Fulkerson算法,用于在有向加权图中找到从源点到汇点的最大流。
- 匹配算法:如匈牙利算法,用于在加权二部图中找到最优匹配。
实际应用
加权图在多个领域有着广泛的应用,包括:
- 物流和运输系统:规划最短路线或最低成本的配送路径。
- 网络通信:优化数据包的传输路径,以减少延迟或提高效率。
- 生物信息学:构建基因或蛋白质网络,分析其相互作用。
- 机器学习:构建基于图的模型,如图神经网络,用于预测和分类任务。
加权图是理解和建模现实世界中复杂关系的重要工具,其研究不仅限于理论数学,也与计算机科学、工程学、经济学和生物学等领域密切相关。
为了更深入理解加权图,我们可以考虑一个具体案例:在一个城市交通网络中寻找两点之间的最短路径。在这个网络中,边的权重代表两个地点之间的行驶时间(或者距离)。我们将使用Dijkstra算法来解决这个问题,该算法是一种用于查找加权图中单源最短路径的经典算法。
背景
假设我们有一个城市,其中有若干个地点和连接它们的道路。每个地点都是图中的一个顶点,而每条道路则是一条有向或无向的边,且每条边都有一个权重,代表驾驶所需的时间。我们的目标是从某个起点出发,找到到达另一个终点的最短路径。
Java源代码实现
首先,我们需要定义加权图的数据结构,然后实现Dijkstra算法。以下是一个简化版的实现:
import java.util.*;class Edge {int dest;int weight;public Edge(int d, int w) {dest = d;weight = w;}
}class Node {List<Edge> neighbors = new ArrayList<>();boolean visited = false;int distance = Integer.MAX_VALUE;Node previous = null;
}public class DijkstraAlgorithm {private List<Node> nodes = new ArrayList<>();public void addNode() {nodes.add(new Node());}public void addEdge(int source, int destination, int weight) {Node srcNode = nodes.get(source);Node destNode = nodes.get(destination);srcNode.neighbors.add(new Edge(destNode, weight));}public void dijkstra(int startNode) {PriorityQueue<Node> queue = new PriorityQueue<>(Comparator.comparingInt(node -> node.distance));Node start = nodes.get(startNode);start.distance = 0;queue.add(start);while (!queue.isEmpty()) {Node current = queue.poll();if (current.visited)continue;for (Edge edge : current.neighbors) {Node neighbor = edge.dest;int tentativeDistance = current.distance + edge.weight;if (tentativeDistance < neighbor.distance) {neighbor.distance = tentativeDistance;neighbor.previous = current;queue.add(neighbor);}}current.visited = true;}}public List<Integer> getPath(int destination) {List<Integer> path = new ArrayList<>();Node current = nodes.get(destination);while (current != null) {path.add(current.hashCode());current = current.previous;}Collections.reverse(path);return path;}public static void main(String[] args) {DijkstraAlgorithm graph = new DijkstraAlgorithm();// 添加节点for (int i = 0; i < 6; i++)graph.addNode();// 添加边graph.addEdge(0, 1, 5);graph.addEdge(0, 2, 3);graph.addEdge(1, 3, 6);graph.addEdge(1, 2, 2);graph.addEdge(2, 4, 4);graph.addEdge(2, 5, 2);graph.addEdge(3, 4, -2); // 负权重边,但Dijkstra不处理负权重环graph.addEdge(4, 5, 1);// 执行Dijkstra算法graph.dijkstra(0);// 输出最短路径System.out.println("Shortest Path to all nodes from node 0:");for (int i = 0; i < graph.nodes.size(); i++) {System.out.println("To node " + i + ": " + graph.getPath(i));}}
}
解析
Edge类定义了边的目的地和权重。Node类定义了顶点的邻居列表、是否访问过、当前距离和前驱节点。DijkstraAlgorithm类实现了加权图的添加节点和边的功能,以及Dijkstra算法的执行。- 主方法中创建图、添加节点和边,执行Dijkstra算法并打印出从起始点到所有其他点的最短路径。
这个Demo展示了如何使用Java实现加权图以及Dijkstra算法的基本框架,实际应用中可能需要根据具体需求进行调整和优化。例如,处理大规模图时,可能需要更高效的数据结构和算法优化,如使用Fibonacci堆代替优先队列。
Demo展示
1. 迷宫游戏:寻找出口
在迷宫游戏中,玩家需要从起点出发,找到通往终点的路径。这可以通过图论中的搜索算法来实现,例如深度优先搜索(DFS)或广度优先搜索(BFS)。
Java代码示例:使用DFS寻找迷宫出口
import java.util.*;public class MazeGame {private static final int[][] DIRECTIONS = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};private char[][] maze;private boolean[][] visited;public MazeGame(char[][] maze) {this.maze = maze;this.visited = new boolean[maze.length][maze[0].length];}private boolean dfs(int x, int y) {if (x < 0 || x >= maze.length || y < 0 || y >= maze[0].length || maze[x][y] == '#' || visited[x][y]) {return false;}if (maze[x][y] == 'E') {return true;}visited[x][y] = true;for (int[] dir : DIRECTIONS) {if (dfs(x + dir[0], y + dir[1])) {return true;}}return false;}public boolean hasPath() {for (int i = 0; i < maze.length; i++) {for (int j = 0; j < maze[0].length; j++) {if (maze[i][j] == 'S') {return dfs(i, j);}}}return false;}public static void main(String[] args) {char[][] maze = {{'#', '#', '#', '#', 'S', '#', '#'},{'#', '.', '.', '.', '.', '.', '#'},{'#', '#', '#', '#', '#', '.', '#'},{'#', '.', '.', '.', '.', '.', '#'},{'#', '#', '#', '#', '#', 'E', '#'}};MazeGame game = new MazeGame(maze);System.out.println(game.hasPath() ? "There is a path." : "There is no path.");}
}
2. 策略游戏:资源收集与管理
在策略游戏中,玩家需要收集资源、建设设施,并管理资源分配。这可以通过构建加权图,其中节点代表资源点或设施,边的权重代表资源的流动成本或收益。
Java代码示例:资源管理加权图
import java.util.*;public class ResourceManagementGame {private Map<String, List<Pair<String, Integer>>> graph = new HashMap<>();public void addNode(String name) {graph.putIfAbsent(name, new ArrayList<>());}public void addEdge(String source, String target, int weight) {graph.get(source).add(new Pair<>(target, weight));}public int calculateTotalResources(String start, int resources) {Set<String> visited = new HashSet<>();Queue<Pair<String, Integer>> queue = new LinkedList<>();queue.add(new Pair<>(start, resources));while (!queue.isEmpty()) {Pair<String, Integer> current = queue.poll();String node = current.getKey();int resource = current.getValue();if (visited.contains(node)) continue;visited.add(node);resource += processNode(node);for (Pair<String, Integer> next : graph.get(node)) {queue.add(new Pair<>(next.getKey(), resource - next.getValue()));}}return resources;}private int processNode(String node) {// Simulate resource processing at each nodereturn node.equals("mine") ? 10 : 0;}public static void main(String[] args) {ResourceManagementGame game = new ResourceManagementGame();game.addNode("mine");game.addNode("factory");game.addNode("warehouse");game.addEdge("mine", "factory", 2);game.addEdge("factory", "warehouse", 3);game.addEdge("warehouse", "mine", 1);System.out.println("Total resources: " + game.calculateTotalResources("mine", 100));}
}class Pair<K, V> {private K key;private V value;public Pair(K key, V value) {this.key = key;this.value = value;}public K getKey() {return key;}public V getValue() {return value;}
}
3. 棋盘游戏:策略与移动
在棋盘游戏中,玩家需要在棋盘上移动棋子以达成胜利条件。棋盘上的每个位置可以视为图中的一个节点,而合法的移动则构成边。
Java代码示例:国际象棋中的骑士走法
import java.util.*;public class ChessKnightMoves {private static final int[][] MOVES = {{2, 1}, {1, 2}, {-1, 2}, {-2, 1}, {-2, -1}, {-1, -2}, {1, -2}, {2, -1}};public int minMoves(int startX, int startY, int endX, int endY) {int[][] board = new int[8][8];Queue<int[]> queue = new LinkedList<>();queue.add(new int[]{startX, startY});board[startX][startY] = 1;while (!queue.isEmpty()) {int[] pos = queue.poll();if (pos[0] == endX && pos[1] == endY) {return board[pos[0]][pos[1]] - 1;}for (int[] move : MOVES) {int newX = pos[0] + move[0];int newY = pos[1] + move[1];if (newX >= 0 && newX < 8 && newY >= 0 && newY < 8 && board[newX][newY] == 0) {queue.add(new int[]{newX, newY});board[newX][newY] = board[pos[0]][pos[1]] + 1;}}}return -1;}public static void main(String[] args) {ChessKnightMoves game = new ChessKnightMoves();System.out.println("Minimum moves: " + game.minMoves(0, 0, 7, 7));}
}
相关文章:

数据结构第14节 加权图
加权图是在图论中一种更为复杂的图结构,它扩展了无向图和有向图的概念,通过给图中的边附加一个数值来表示边的某种属性,如成本、距离、容量或相似度等。这个数值被称为边的“权重”。 定义 加权图可以被形式化地定义为一个三元组 ( G (V, …...

128陷阱(超详细)
int x 128;int y 128;int n 127;int m 127;Integer d Integer.valueOf(x);Integer g Integer.valueOf(y);Integer z Integer.valueOf(n);Integer v Integer.valueOf(m);System.out.println(d g);System.out.println(z v); 思考一下他的结果是什么? 为什么…...

STM32自己从零开始实操08:STM32主控原理图
由于老师使用的各引脚分门别类的单片机原理图我没有找到,我使用是引脚按顺序摆放的,不方便一个模块一个模块截图展示,所以这部分使用老师的原理图。 一、电源 1.1电源的介绍 1.1.1数字电源和地(VDD和VSS) 数字电源…...
Ubuntu20.04配置TurtleBot3 Waffle Pi远程控制
这里写目录标题 0. 机器人配置1. Ubuntu20.04配置TurtleBot3 Waffle Pi远程控制1.1 TurtleBot3 Waffle Pi端配置1.2 PC端配置1.2.1 安装turtlebot3的环境配置1.2.2 创建项目并安装Turtlebot31.2.3 配置环境变量 1.3 PC端与TurtleBot3进行通信1.3.1 PC端与机器人端互PING和SSH连…...

SaaS产品和独立部署型产品有什么区别,该怎么选择?
随着云计算和软件服务的多样化,产品形式主要划分SaaS型(开通即用)和独立部署(完整交付)两种模式,那么SaaS产品和独立部署产品有哪些区别,我们在选择产品的时候应该如何去抉择?本文我…...
【Linux】压缩命令——gzip,bzip2,xz
1.压缩文件的用途与技术 你是否有过文件太大,导致无法以正常的E-mail方式发送?又或学校、厂商要求使用CD或DVD来做数据归档之用,但是你的单一文件却都比这些传统的一次性存储媒介还要大,那怎么分成多块来刻录?还有&am…...

【Java13】包
“包”这个机制,类似于分组。主要作用是区分不同组内的同名类。例如,高三三班有一个“王五”,高二八班也有一个“王五”。高三三班和高三八班就是两个不同的包。 Java中的包(package)机制主要提供了类的多层命名空间&…...

从零到一:Python自动化测试的详细指南!
引言: Python是一种功能强大且易于学习和使用的编程语言,它非常适合用于自动化测试。本文将从零开始,通过详细的步骤和规范,介绍如何在Python中实施高质量的自动化测试。我们将探讨测试策略的制定、测试框架的选择、测试用例的编…...

iOS中多个tableView 嵌套滚动特性探索
嵌套滚动的机制 目前的结构是这样的,整个页面是一个大的tableView, Cell 是整个页面的大小,cell 中嵌套了一个tableView 通过测试我们发现滚动的时候,系统的机制是这样的, 我们滑动内部小的tableView, 开始滑动的时候,…...

TCP/IP模型和OSI模型的区别
OSI模型, 是国际标准化组织(ISO)制定的一个用于计算机或通信系统间互联的标准体系,将计算机网络通信划分为七个不同的层级,每个层级都负责特定的功能。每个层级都构建在其下方的层级之上,并为上方的层级提供…...
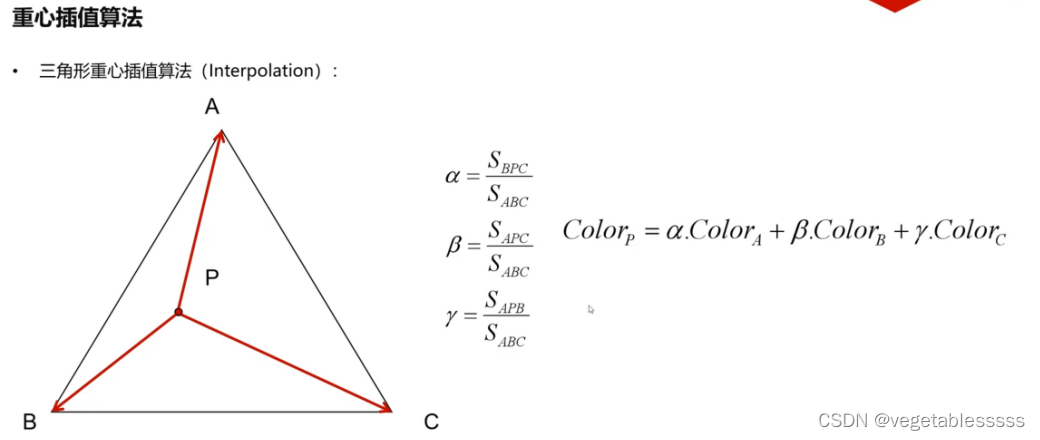
(九)绘制彩色三角形
前面的学习中并未涉及到颜色,现在打算写一个例子,在顶点着色器和片元着色器中加入颜色,绘制有颜色的三角形。 #include <glad/glad.h>//glad必须在glfw头文件之前包含 #include <GLFW/glfw3.h> #include <iostream>void …...

短信群发平台适用于哪些行业?
短信群发平台作为一种高效、快速且成本相对较低的通信方式,适用于多个行业。以下是一些主要适用行业的概述: 1. 零售与电商行业 应用场景:零售和电商企业可以利用短信群发进行新品推广、促销信息发布、订单状态更新、物流跟踪通知等。 2. 金…...

1. 倍数
倍数 题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 请问在 11 到 20202020 中,有多少个数既是 44 的整数倍,又是 66 的整数倍。 运行限制 最大运行时间:1s最大运行内存: 12…...

C#常用关键字举例
关键字是 C# 编译器预定义的保留字。这些关键字不能用作标识符,但是,如果您想使用这些关键字作为标识符,可以在关键字前面加上 字符作为前缀。 class: public class MyClass {// Class definition }interface: public interface IMyInterfac…...

stm32——外部中断EXTI
上回书说到定时器的级联,今天来谈谈外部中断EXTI。我使用的是STM32F103C8T6的学习板。仅供大家参考。 什么是中断呢?中断是指计算机在执行程序的过程中,当出现某些异常情况或特殊事件(例如外部设备请求、定时时间到达、程序错误等…...

Solidity:变量数据存储和作用域 storage/memory/calldata
Solidity中的引用类型 引用类型(Reference Type):包括数组(array)和结构体(struct),由于这类变量比较复杂,占用存储空间大,我们在使用时必须要声明数据存储的位置。 数据位置 …...
ElementUI中的el-table解决宽度问题 - 根据内容自动撑开
在使用element-ui中,会发现表格组件el-table在未指定宽度情况下,会自动计算并给表格宽度赋值。但实际开发中,有时需要根据内容实际长度自动撑开显示,由内容的多少而决定表格的宽度,而不是默认宽度为100%。在默认情况下…...

react apollo hooks
1、创建ApolloProvider来包装整个程序 <ApolloProvider client{client}><App /> <ApolloProvider> 2、useQuery查询 工作方式usequery将返回一个数组 const {要返回的对象} useQuery(传入参数) 实例 const query gqlquery name {whatever {field}} e…...

Android 10.0 SystemUI启动流程
1、手机开机后,Android系统首先会创建一个Zygote(核心进程)。 2、由Zygote启动SystemServer。 3、SystemServer会启动系统运行所需的众多核心服务和普通服务、以及一些应用及数据。例如:SystemUI 启动就是从 SystemServer 里启动的…...

洛谷 P1032 [NOIP2002 提高组] 字串变换
P1032 [NOIP2002 提高组] 字串变换 - 洛谷 | 计算机科学教育新生态 题目来源 洛谷 题目内容 [NOIP2002 提高组] 字串变换 题目背景 本题不保证存在靠谱的多项式复杂度的做法。测试数据非常的水,各种做法都可以通过,不代表算法正确。因此本题题目和…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...
