上海市计算机学会竞赛平台2024年6月月赛丙组超级奇数
题目描述
如果一个十进制数的所有数字都是奇数,则称之为超级奇数,例如 35733573 就是一个超级奇数,而 3141531415 不是。按照从小到大排序,前几名的超级奇数为
1,3,5,7,9,11,13,15,17,⋯1,3,5,7,9,11,13,15,17,⋯
给定一个超级奇数 𝑛n,请输出 𝑛n 在所有超级奇数中的排名。
输入格式
- 单个整数表示 𝑛n
输出格式
- 单个整数表示答案
数据范围
- 30%30% 的数据,1≤𝑛≤1,0001≤n≤1,000
- 60%60% 的数据,1≤𝑛≤1,000,0001≤n≤1,000,000
- 100%100% 的数据,1≤𝑛≤1,000,000,0001≤n≤1,000,000,000
样例数据
输入:
111
输出:
31
详见代码:
#include <bits/stdc++.h>
using namespace std;
string n;
long long ans = 0;
int main()
{cin >> n;for(int i = 0; i < n.length(); i++) {int x = (n[i] - '0') / 2 + 1;ans = ans * 5 + x;}cout << ans;return 0;
}相关文章:

上海市计算机学会竞赛平台2024年6月月赛丙组超级奇数
题目描述 如果一个十进制数的所有数字都是奇数,则称之为超级奇数,例如 35733573 就是一个超级奇数,而 3141531415 不是。按照从小到大排序,前几名的超级奇数为 1,3,5,7,9,11,13,15,17,⋯1,3,5,7,9,11,13,15,17,⋯ 给定一个超级…...

速盾:cdn业务优化
CDN(Content Delivery Network)是一种基于互联网的分布式网络架构,旨在提供更快速、可靠的内容传输服务。它通过将内容分发至多个节点,使用户可以从离他们更近的节点获取内容,从而提高访问速度和用户体验。 然而&…...

重生奇迹mu的地图名
地图之一:勇者大陆 勇者大陆地处奇迹大陆中央。终年阴雨连绵,气候潮湿闷热。植物由充满黑暗阴森气氛的草地所构成。这里的NPC数量是所有地图中最多的。因为地步交通要冲,所以也是玩家聚集最多的地方。 这里是剑士、魔法师、魔剑士和圣导师初…...

【CSS】缩写属性gap
在CSS Grid Layout(网格布局)和Flexbox(弹性盒布局)中,gap 是一个缩写属性,用于同时设置行间隙(gutter)和列间隙(在Flexbox中通常称为“交叉轴间隙”)的大小。…...
:子程序和模块)
Perl 语言开发(八):子程序和模块
目录 1. 引言 2. 子程序的基本概念与用法 2.1 子程序的定义和调用 2.2 传递参数 2.3 返回值 2.4 上下文和返回值 3. 模块的基本概念与用法 3.1 模块的定义 3.2 使用模块 3.3 导出符号 3.4 模块的文件结构和命名 4. 实际应用中的子程序与模块 4.1 子程序参数验证与…...

自注意力机制和多头注意力机制区别
Ref:小白看得懂的 Transformer (图解) Ref:一文彻底搞懂 Transformer(图解手撕) 多头注意力机制(Multi-Head Attention)和自注意力机制(Self-Attention)是现代深度学习模型&#x…...

数据结构第14节 加权图
加权图是在图论中一种更为复杂的图结构,它扩展了无向图和有向图的概念,通过给图中的边附加一个数值来表示边的某种属性,如成本、距离、容量或相似度等。这个数值被称为边的“权重”。 定义 加权图可以被形式化地定义为一个三元组 ( G (V, …...

128陷阱(超详细)
int x 128;int y 128;int n 127;int m 127;Integer d Integer.valueOf(x);Integer g Integer.valueOf(y);Integer z Integer.valueOf(n);Integer v Integer.valueOf(m);System.out.println(d g);System.out.println(z v); 思考一下他的结果是什么? 为什么…...

STM32自己从零开始实操08:STM32主控原理图
由于老师使用的各引脚分门别类的单片机原理图我没有找到,我使用是引脚按顺序摆放的,不方便一个模块一个模块截图展示,所以这部分使用老师的原理图。 一、电源 1.1电源的介绍 1.1.1数字电源和地(VDD和VSS) 数字电源…...
Ubuntu20.04配置TurtleBot3 Waffle Pi远程控制
这里写目录标题 0. 机器人配置1. Ubuntu20.04配置TurtleBot3 Waffle Pi远程控制1.1 TurtleBot3 Waffle Pi端配置1.2 PC端配置1.2.1 安装turtlebot3的环境配置1.2.2 创建项目并安装Turtlebot31.2.3 配置环境变量 1.3 PC端与TurtleBot3进行通信1.3.1 PC端与机器人端互PING和SSH连…...

SaaS产品和独立部署型产品有什么区别,该怎么选择?
随着云计算和软件服务的多样化,产品形式主要划分SaaS型(开通即用)和独立部署(完整交付)两种模式,那么SaaS产品和独立部署产品有哪些区别,我们在选择产品的时候应该如何去抉择?本文我…...
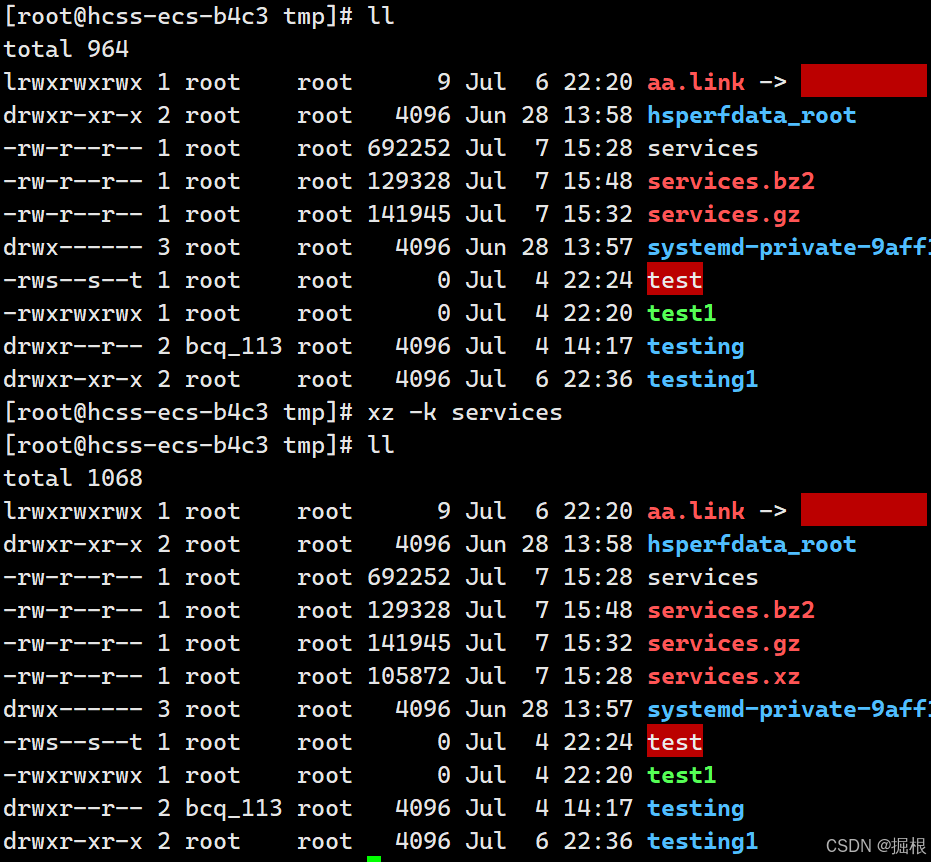
【Linux】压缩命令——gzip,bzip2,xz
1.压缩文件的用途与技术 你是否有过文件太大,导致无法以正常的E-mail方式发送?又或学校、厂商要求使用CD或DVD来做数据归档之用,但是你的单一文件却都比这些传统的一次性存储媒介还要大,那怎么分成多块来刻录?还有&am…...

【Java13】包
“包”这个机制,类似于分组。主要作用是区分不同组内的同名类。例如,高三三班有一个“王五”,高二八班也有一个“王五”。高三三班和高三八班就是两个不同的包。 Java中的包(package)机制主要提供了类的多层命名空间&…...

从零到一:Python自动化测试的详细指南!
引言: Python是一种功能强大且易于学习和使用的编程语言,它非常适合用于自动化测试。本文将从零开始,通过详细的步骤和规范,介绍如何在Python中实施高质量的自动化测试。我们将探讨测试策略的制定、测试框架的选择、测试用例的编…...

iOS中多个tableView 嵌套滚动特性探索
嵌套滚动的机制 目前的结构是这样的,整个页面是一个大的tableView, Cell 是整个页面的大小,cell 中嵌套了一个tableView 通过测试我们发现滚动的时候,系统的机制是这样的, 我们滑动内部小的tableView, 开始滑动的时候,…...

TCP/IP模型和OSI模型的区别
OSI模型, 是国际标准化组织(ISO)制定的一个用于计算机或通信系统间互联的标准体系,将计算机网络通信划分为七个不同的层级,每个层级都负责特定的功能。每个层级都构建在其下方的层级之上,并为上方的层级提供…...
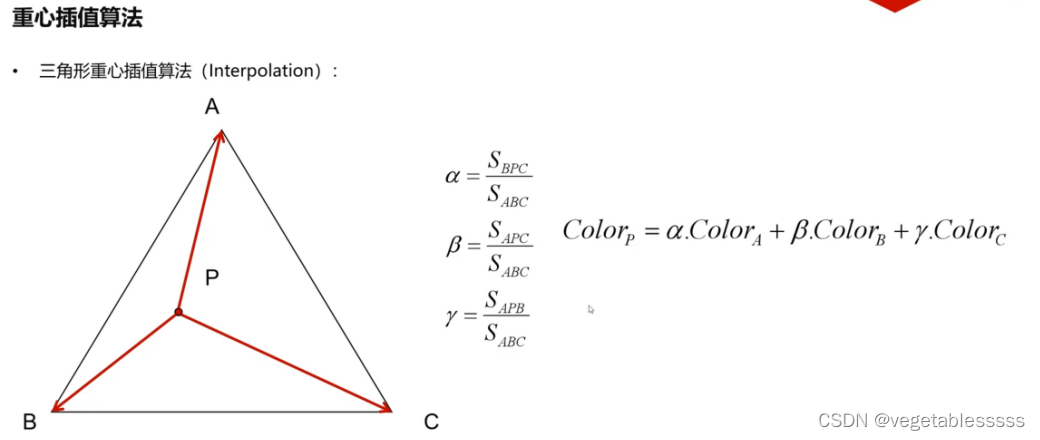
(九)绘制彩色三角形
前面的学习中并未涉及到颜色,现在打算写一个例子,在顶点着色器和片元着色器中加入颜色,绘制有颜色的三角形。 #include <glad/glad.h>//glad必须在glfw头文件之前包含 #include <GLFW/glfw3.h> #include <iostream>void …...

短信群发平台适用于哪些行业?
短信群发平台作为一种高效、快速且成本相对较低的通信方式,适用于多个行业。以下是一些主要适用行业的概述: 1. 零售与电商行业 应用场景:零售和电商企业可以利用短信群发进行新品推广、促销信息发布、订单状态更新、物流跟踪通知等。 2. 金…...

1. 倍数
倍数 题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 请问在 11 到 20202020 中,有多少个数既是 44 的整数倍,又是 66 的整数倍。 运行限制 最大运行时间:1s最大运行内存: 12…...

C#常用关键字举例
关键字是 C# 编译器预定义的保留字。这些关键字不能用作标识符,但是,如果您想使用这些关键字作为标识符,可以在关键字前面加上 字符作为前缀。 class: public class MyClass {// Class definition }interface: public interface IMyInterfac…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

Python爬虫实战:研究Restkit库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的有价值数据。如何高效地采集这些数据并将其应用于实际业务中,成为了许多企业和开发者关注的焦点。网络爬虫技术作为一种自动化的数据采集工具,可以帮助我们从网页中提取所需的信息。而 RESTful API …...
