王道考研数据机构:中缀表达式转为后缀表达式
实现方法:
初始化一个栈,用于保存暂时还不能确定运算顺序的运算符。从左到右处理各个元素,直到末尾。可能遇到三种情况:
- 遇到操作数。直接加入后缀表达式
- 遇到界限符。遇到“(”直接入栈;遇到“)”则依次弹出栈内运算符并加入后缀表达式,直到弹出“(”为止。注意:“(”不加入后缀表达式。
- 遇到运算符。依次弹出栈中优先级高于或等于当前运算符的所有运算符,并加入后缀表达式,若磁到“(”或栈空则停止。之后再把当前运算符入栈。
按上述方法处理完所有字符后,将栈中剩余运算符依次弹出,并加入后缀表达式。
#include<stdio.h>
#include<malloc.h>
#define MaxSize 100
typedef struct Stack{char data[MaxSize];int top;
}Stack;
void initStack(Stack* &S){S = (Stack *)malloc(sizeof(Stack));S->top=-1;
}
bool push(Stack * &S, char e){if(S->top == MaxSize - 1)return false;S->data[++S->top] = e;printf("元素%c进栈\n",e);return true;
}
bool pop(Stack * &S,char &e){if(S->top==-1)return false;e = S->data[S->top--];printf("元素%c出栈\n",e);return true;
}
bool getTop(Stack * &S, char &e){if(S->top==-1)return false;e = S->data[S->top];return true;
}
bool emptyStack(Stack * &S){return S->top==-1;
}
int getSymbolPriority(char c){if(c=='+'||c=='-')return 1;elsereturn 2;
}
int main()
{Stack *s;char str[MaxSize];//中缀表达式 char houZhui[MaxSize];//后缀表达式 int index=0;scanf("%s",str);initStack(s);for(int i=0;str[i]!='\0';i++){printf("第%d次操作\n",i+1); if(str[i]=='+' || str[i]=='-' || str[i]=='*' || str[i]=='/'){int v1 = getSymbolPriority(str[i]);while(!emptyStack(s)){char e;getTop(s,e);if(e=='(')break;int v2 = getSymbolPriority(e);if(v2>=v1){pop(s,e);houZhui[index++]=e;}elsebreak;}push(s,str[i]);}else if(str[i]=='(' || str[i]==')'){if(str[i]=='(')push(s,str[i]);elsewhile(!emptyStack(s)){char e;getTop(s,e);if(e=='('){pop(s,e);break;c}else{pop(s,e);houZhui[index++]=e;} }}else{houZhui[index++]=str[i];}printf("此时后缀表达式元素为:");for(int j=0;j<index;j++)printf("%c",houZhui[j]);printf("\n\n\n"); }printf("栈中剩余元素依次弹出:\n");while(!emptyStack(s)){char e;pop(s,e);houZhui[index++]=e;}printf("\n最终结果为:\n");for(int i=0;i<index;i++)printf("%c",houZhui[i]);return 0;
}
//A+B-C*D/E+F
//A+B*(C-D)-E/F运行结果:
输入:
A+B-C*D/E+F
输出:
第1次操作
此时后缀表达式元素为:A第2次操作
元素+进栈
此时后缀表达式元素为:A第3次操作
此时后缀表达式元素为:AB第4次操作
元素+出栈
元素-进栈
此时后缀表达式元素为:AB+第5次操作
此时后缀表达式元素为:AB+C第6次操作
元素*进栈
此时后缀表达式元素为:AB+C第7次操作
此时后缀表达式元素为:AB+CD第8次操作
元素*出栈
元素/进栈
此时后缀表达式元素为:AB+CD*第9次操作
此时后缀表达式元素为:AB+CD*E第10次操作
元素/出栈
元素-出栈
元素+进栈
此时后缀表达式元素为:AB+CD*E/-第11次操作
此时后缀表达式元素为:AB+CD*E/-F栈中剩余元素依次弹出:
元素+出栈A+B-C*D/E+F
转为后缀表达式最终结果为:
AB+CD*E/-F+
输入:
A+B*(C-D)-E/F
输出
第1次操作
此时后缀表达式元素为:A第2次操作
元素+进栈
此时后缀表达式元素为:A第3次操作
此时后缀表达式元素为:AB第4次操作
元素*进栈
此时后缀表达式元素为:AB第5次操作
元素(进栈
此时后缀表达式元素为:AB第6次操作
此时后缀表达式元素为:ABC第7次操作
元素-进栈
此时后缀表达式元素为:ABC第8次操作
此时后缀表达式元素为:ABCD第9次操作
元素-出栈
元素(出栈
此时后缀表达式元素为:ABCD-第10次操作
元素*出栈
元素+出栈
元素-进栈
此时后缀表达式元素为:ABCD-*+第11次操作
此时后缀表达式元素为:ABCD-*+E第12次操作
元素/进栈
此时后缀表达式元素为:ABCD-*+E第13次操作
此时后缀表达式元素为:ABCD-*+EF栈中剩余元素依次弹出:
元素/出栈
元素-出栈A+B*(C-D)-E/F
转为后缀表达式最终结果为:
ABCD-*+EF/-
相关文章:

王道考研数据机构:中缀表达式转为后缀表达式
实现方法: 初始化一个栈,用于保存暂时还不能确定运算顺序的运算符。从左到右处理各个元素,直到末尾。可能遇到三种情况: 遇到操作数。直接加入后缀表达式遇到界限符。遇到“(”直接入栈;遇到“)”则依次弹出栈内运算符并加入后缀表达式&…...

PL/SQL安装+汉化教程
PL/SQL安装教程 一、安装: 登陆官网:PL/SQL Developer - Allround Automations下载 下载PL/SQL稳定版本12.0.7 根据自己计算机版本安装相适配的版本。我这里安装X64-bit版本 进行安装: 根据情况去更改安装,我这里全部下一步…...

Qt | Qt 线程相关类概述和举例
Qt 是一个广泛用于跨平台应用开发的框架。在 Qt 中,多线程支持是其核心特性之一,它允许开发者在不同平台上创建并发应用。以下是 Qt 中与线程相关的类概述及其使用示例。 Qt 中的线程相关类 QThread QThread 是 Qt 中用于创建和管理线程的基类。通过派生并重写 run() 函数…...

Linux 复现Docker NAT网络
Linux 复现Docker NAT网络 docker 网络的构成分为宿主机docker0网桥和为容器创建的veth 对构成。这个默认网络命名空间就是我们登陆后日常使用的命名空间 使用ifconfig命令查看到的就是默认网络命名空间,docker0就是网桥,容器会把docker0当成路由&…...

HBuilder X 小白日记03-用css制作简单的交互动画
:hover选择器,用于选择鼠标指针浮动在上面的元素。 :hover选择器可用于所有元素,不只是链接 :link选择器 设置指向未被访问页面的链接的样式 :visited选择器 用于设置指向已被访问的页面的链接 :active选择器 用于活动链接...

【深度学习练习】心脏病预测
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 一、什么是RNN RNN与传统神经网络最大的区别在于,每次都会将前一次的输出结果,带到下一隐藏层中一起训练。如下图所示: …...

创建react的脚手架
Create React App 中文文档 (bootcss.com) 网址:creat-react-app.bootcss.com 主流的脚手架:creat-react-app 创建脚手架的方法: 方法一(JS默认): 1. npx create-react-app my-app 2. cd my-app 3. …...

用例导图CMind
突然有一些觉悟,程序猿不能只会吭哧吭哧的低头做事,应该学会怎么去展示自己,怎么去宣传自己,怎么把自己想做的事表述清楚。 于是,这两天一直在整理自己的作品,也为接下来的找工作多做点准备。接下来…...

C++ 仿函数
一、介绍 CSTL中的仿函数,又被称为函数对象,其实就是:重载了()运算符的类。 因为在使用重载的operator()时,类似于函数调用,因此被称为仿函数。 ※注意※:仿函数本质上是一个类,不是函数。 二…...
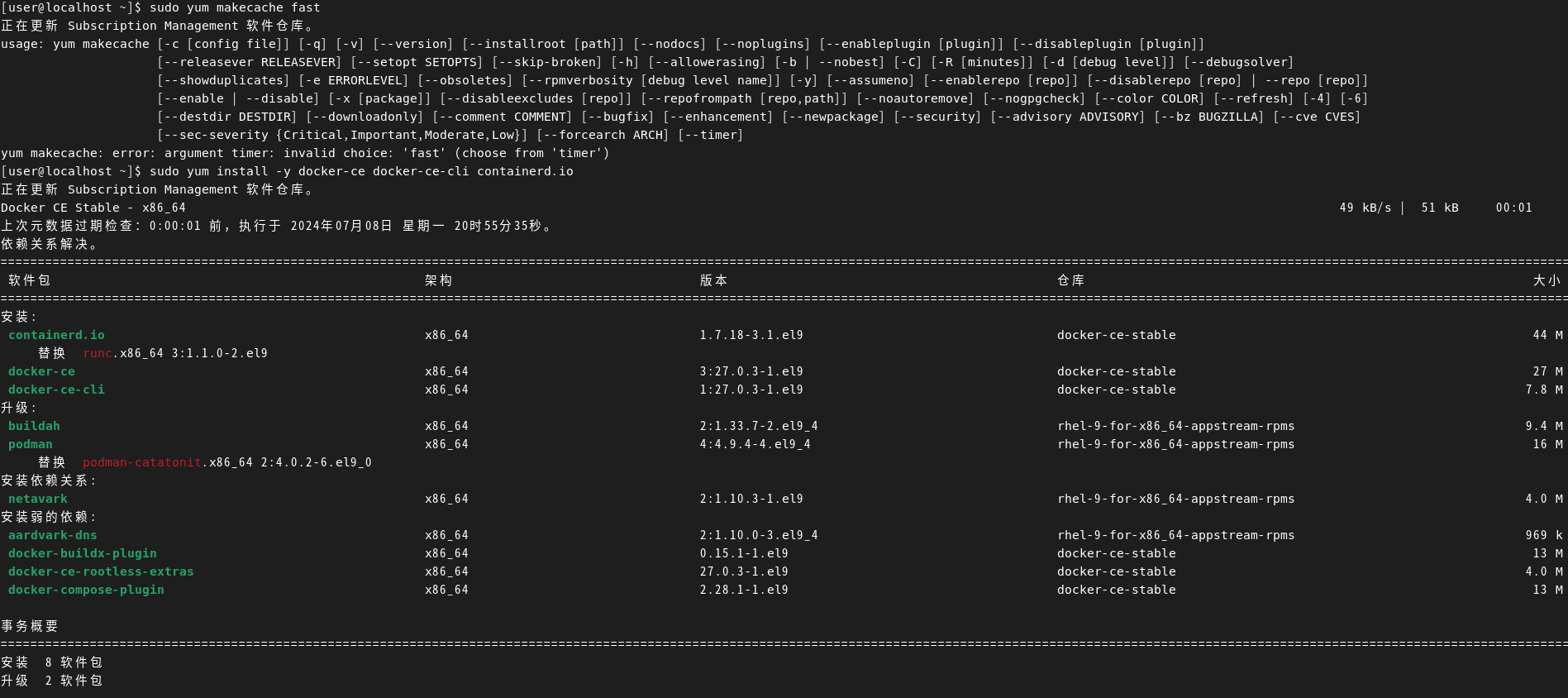
Redhat 安装 docker 网络连接超时问题
目录 添加阿里云的Docker CE仓库 更新YUM缓存 安装 Docker Engine 启动并设置Docker自启动 验证 Docker 安装 [userlocalhost ~]$ sudo yum-config-manager --add-repohttps://download.docker.com/linux/centos/docker-ce.repo 正在更新 Subscription Management 软件仓库…...

Java面试题:undo log和redo log
undo log和redo log的区别 缓冲池(buffer pool): 主内存中的一个区域,可以缓存磁盘上经常被操作的数据,在执行crud时先操作缓冲池的数据以减少磁盘io 数据页(page): InnoDB存储引擎管理的最小单元,每页大小为16kb,页中存储的是行数据 redo log 重做日志,用来实现任务的持…...

【Scrapy】Scrapy 中间件等级设置规则
准我快乐地重饰演某段美丽故事主人 饰演你旧年共寻梦的恋人 再去做没流着情泪的伊人 假装再有从前演过的戏份 重饰演某段美丽故事主人 饰演你旧年共寻梦的恋人 你纵是未明白仍夜深一人 穿起你那无言毛衣当跟你接近 🎵 陈慧娴《傻女》 Scrapy 是…...

SDK环境的安装(测试使用)
1、安装 将文件解压至目录,我的目录为:D:\Program Files\Android 解压后如下: 下载链接如下: sdk下载 提取码见文章最后: 2、配置环境 1、在环境变量中,选择系统变量,点击新建。 变量名:ANDROID_HOME 变量值:“你自己的android-sdk安装路径” (例如我的:D:\Pro…...
【matlab】【python】爬虫实战
目录 引言 具体步骤 1.设置请求选项 2.发送请求并获取响应 3.设置正则表达式 4.执行正则表达式匹配 matlab完整代码 python代码示例 引言 在当今这个信息爆炸的时代,数据已成为推动社会进步和企业发展的核心动力之一。随着互联网的普及和技术的飞速发展&am…...

Android TV跨平台开发心得
这半年来陆陆续续做了一堆poc,刚开始是flutter,结果领导叫停了,说有其他部门做一样的事,真不巧;后来是react native,开发了个demo,上报上去了已经;现在又要做android nativewebview …...

View->裁剪框View的绘制,手势处理
XML文件 <?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android…...

语言模型的进化:从NLP到LLM的跨越之旅
在人工智能的浩瀚宇宙中,自然语言处理(NLP)一直是一个充满挑战和机遇的领域。随着技术的发展,我们见证了从传统规则到统计机器学习,再到深度学习和预训练模型的演进。如今,我们站在了大型语言模型ÿ…...

应急响应--网站(web)入侵篡改指南
免责声明:本文... 目录 被入侵常见现象: 首要任务: 分析思路: 演示案例: IIS&.NET-注入-基于时间配合日志分析 Apache&PHP-漏洞-基于漏洞配合日志分析 Tomcat&JSP-弱口令-基于后门配合日志分析 (推荐) Webshell 查杀-常规后门&…...
vue3+vue-router+vite 实现动态路由
文章中出现的代码是演示版本,仅供参考,实际的业务需求会更加复杂 什么是动态路由 什么场景会用到动态路由 举一个最常见的例子,比如说我们要开发一个后台管理系统,一般来说后台管理系统都会分角色登录,这个时候也就涉…...
Okhttp hostnameVerifier详解
hostnameVerifier 方法简介核心原理参考资料 方法简介 本篇博文以Okhttp 4.6.0来解析hostnameVerfier的作用,顾名思义,该方法的主要作用就是鉴定hostnname的合法性。Okhttp在初始化的时候我们可以自己配置hostnameVerfier: new OkHttpClien…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...
