核函数的深入理解
核函数 (Kernel Function)是一种在高维特征空间中隐式计算内积的方法,它允许在原始低维空间中通过一个简单的函数来实现高维空间中的内积计算,而无需显式地计算高维特征向量。
核函数 的基本思想是通过一个映射函数 ϕ \phi ϕ 将原始数据从低维空间映射到高维空间。假设有两个数据点 x x x 和 y y y,在低维空间中的内积是 ⟨ x , y ⟩ \langle x, y \rangle ⟨x,y⟩。映射到高维空间后,内积变为 ⟨ ϕ ( x ) , ϕ ( y ) ⟩ \langle \phi(x), \phi(y) \rangle ⟨ϕ(x),ϕ(y)⟩。核函数 K K K 定义为:
K ( x , y ) = ⟨ ϕ ( x ) , ϕ ( y ) ⟩ K(x, y) = \langle \phi(x), \phi(y) \rangle K(x,y)=⟨ϕ(x),ϕ(y)⟩
关键在于,核函数 K K K 可以直接计算出高维空间中的内积,而不需要显式地计算 ϕ ( x ) \phi(x) ϕ(x) 和 ϕ ( y ) \phi(y) ϕ(y)。这种方法的优势在于,高维空间中的计算可能非常复杂和耗时,而核函数提供了一种高效的方式来处理这些计算。
常见的核函数包括:
- 线性核函数: K ( x , y ) = ⟨ x , y ⟩ K(x, y) = \langle x, y \rangle K(x,y)=⟨x,y⟩
- 多项式核函数: K ( x , y ) = ( ⟨ x , y ⟩ + c ) d K(x, y) = (\langle x, y \rangle + c)^d K(x,y)=(⟨x,y⟩+c)d
- 高斯径向基函数(RBF)核函数: K ( x , y ) = exp ( − ∥ x − y ∥ 2 2 σ 2 ) K(x, y) = \exp\left(-\frac{\|x - y\|^2}{2\sigma^2}\right) K(x,y)=exp(−2σ2∥x−y∥2)
- Sigmoid核函数: K ( x , y ) = tanh ( α ⟨ x , y ⟩ + c ) K(x, y) = \tanh(\alpha \langle x, y \rangle + c) K(x,y)=tanh(α⟨x,y⟩+c)
通过选择合适的核函数,可以在低维空间中隐式地进行高维空间的内积计算,从而实现非线性分类和回归等任务。
核函数 K ( x , y ) K(x, y) K(x,y) 之所以能够直接给出高维空间中内积的结果,而无需实际计算 ϕ ( x ) \phi(x) ϕ(x) 和 ϕ ( y ) \phi(y) ϕ(y),是因为核函数本身具有特定的数学性质,特别是满足 Mercer 条件。Mercer 条件 确保了核函数可以表示为某个高维特征空间中的内积。
具体来说,核函数 K ( x , y ) K(x, y) K(x,y) 是一个对称函数,满足对于任意有限输入集和任意实值函数 f f f,有:
∬ K ( x , y ) f ( x ) f ( y ) d x d y ≥ 0 \iint K(x, y) f(x) f(y) \, dx \, dy \geq 0 ∬K(x,y)f(x)f(y)dxdy≥0
这意味着 K ( x , y ) K(x, y) K(x,y) 是一个半正定函数。根据 Mercer 定理,任何满足 Mercer 条件的核函数 K ( x , y ) K(x, y) K(x,y) 都可以表示为某个特征映射 ϕ \phi ϕ 的内积,即:
K ( x , y ) = ⟨ ϕ ( x ) , ϕ ( y ) ⟩ K(x, y) = \langle \phi(x), \phi(y) \rangle K(x,y)=⟨ϕ(x),ϕ(y)⟩
这里的 ϕ \phi ϕ 是将数据从原始空间映射到高维特征空间的函数。关键在于,不需要知道 ϕ \phi ϕ 的具体形式,只需要知道核函数 K ( x , y ) K(x, y) K(x,y) 的定义,就可以直接计算高维空间中的内积。
这种隐式计算的优势在于:
- 计算效率:在高维空间中显式计算特征向量 ϕ ( x ) \phi(x) ϕ(x) 和 ϕ ( y ) \phi(y) ϕ(y) 可能非常耗时和复杂,而核函数提供了一种更高效的方式来处理这些计算。
- 避免维度灾难:在高维空间中,特征向量的维度可能非常高,甚至无穷大,这会导致计算上的困难。核函数允许在低维空间中进行计算,避免了直接处理高维数据的复杂性。
相关文章:

核函数的深入理解
核函数 (Kernel Function)是一种在高维特征空间中隐式计算内积的方法,它允许在原始低维空间中通过一个简单的函数来实现高维空间中的内积计算,而无需显式地计算高维特征向量。 核函数 的基本思想是通过一个映射函数 ϕ \phi ϕ …...
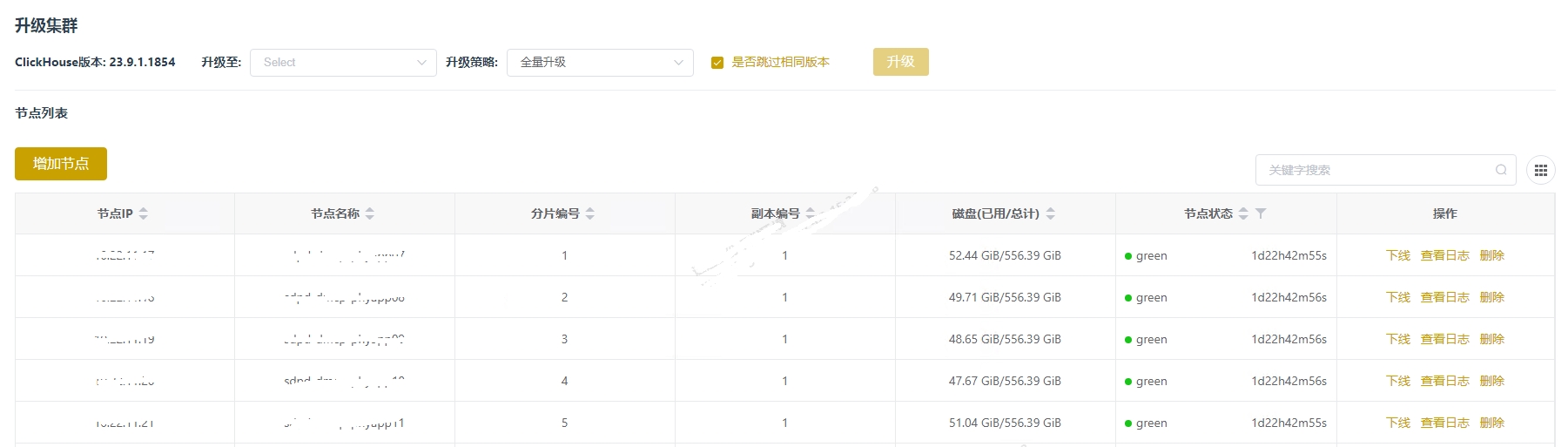
使用Ckman部署ClickHouse集群介绍
使用Ckman部署ClickHouse集群介绍 1. Ckman简介 ClickHouse Manager是一个为ClickHouse数据库量身定制的管理工具,它是由擎创科技数据库团队主导研发的一款用来管理和监控ClickHouse集群的可视化运维工具。目前该工具已在github上开源,开源地址为&…...

「前端工具」postman接口测试工具详解
Postman 是一款流行的 API 开发工具,用于构建和测试 RESTful API。以下是 Postman 的一些关键特性和使用方法的详解: 1. 界面和基本操作 工作区:Postman 的主界面,用于显示集合、环境和全局变量。请求构建器:用于输入请求的 URL、HTTP 方法、请求头、请求体等。响应区:显…...

生成requirements.txt
pip install pipreqs pipreqs ./ --encodingutf-8 --force python导出requirements.txt的几种方法总结...

ubuntu ceph部署
ubuntu ceph部署 参考文档:http://docs.ceph.org.cn/start/ 节点配置 1个mon节点,3个osd节点 安装前准备 安装ceph-deploy 添加 release key wget -q -O- https://download.ceph.com/keys/release.asc | sudo apt-key add -添加Ceph软件包源&…...

2024.7.8
2024.7.8 【追逐影子的人,自己就是影子 —— 荷马】 Monday 六月初三 讲的根本听不懂好吧! 目前只写了三道题(但是黑色 确实是没见过这么抽象的数据结构 Gregor and the Two Painters Number of Components Equal LCM Subsets 这个lcm确实…...

Spring 外部jar包Bean自动装配
Spring 外部jar包Bean自动装配 背景介绍 公共代码模块被作为jar包引入业务项目,前者定义的bean即使添加了Component注解由于不会被扫描到也就无法被Spring管理。此处通过Spring SPI机制来完成 使用 spring.factories 在外部 jar 包中创建 spring.factories 文件&a…...

2通道音频ADC解码芯片ES7243L、ES7243E、ES7243,用于低成本实现模拟麦克风转换为IIS数字话筒
前言: 音频解码芯片某创参考价格: ES7243L 500:¥1.36 / 个 ES7243E 500:¥1.66 / 个 ES7243 500: ¥1.91 / 个 其中ES7243L工作电压为1.8V,与其他两款的3.3V工作电压不同&…...
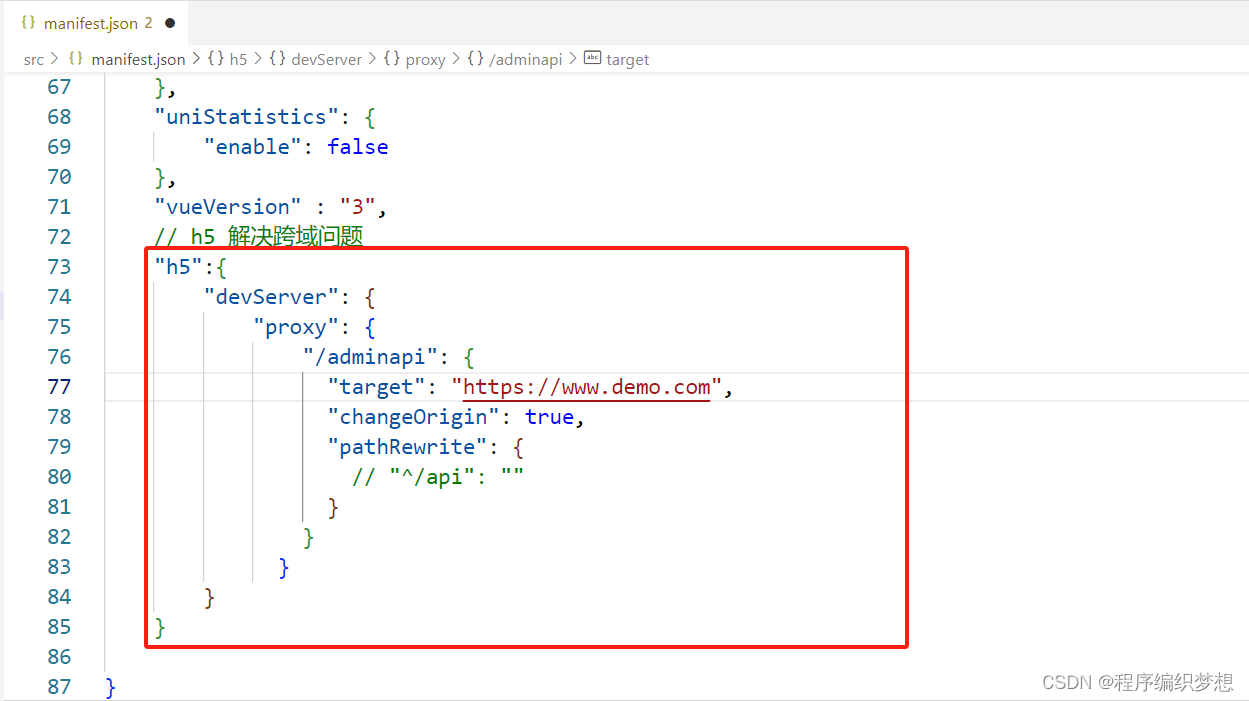
uniapp跨域问题解决
找到menifest文件,在文件的最后添加如下代码: // h5 解决跨域问题"h5":{"devServer": {"proxy": {"/adminapi": {"target": "https://www.demo.com", // 目标访问网址"changeOrigin…...

[C++][ProtoBuf][Proto3语法][一]详细讲解
目录 1.字段规则2.消息类型的定义与使用1.定义2.使用 3.enum类型1.语法2.定义时注意3.代码 1.字段规则 消息的字段可以⽤下⾯⼏种规则来修饰: singular:消息中可以包含该字段零次或⼀次(不超过⼀次) proto3语法中,字段默认使⽤该规则 repeat…...

千古雄文《渔樵问对》原文、译文、解析
邵雍《渔樵问对》:开悟奇文,揭示世界的终极意义 【邵雍《渔樵问对》:开悟奇文,揭示世界的终极意义】 邵雍(1011年1月21日-1077年7月27日,宋真宗大中祥符四年十二月二十五日戌时生至神宗熙宁十…...

uniapp 开发备忘录-防坑指南
uniapp 开发备忘录-防坑指南 npm run dev:mp-weixin 编译微信小程序报错: [plugin:uni:mp-using-component] Expected ‘,’ or ‘}’ after property value in JSON at position 解决方案:升级uniapp 到最新 alpha 版。(2024年7月13日&am…...

Simple_ReAct_Agent
参考自https://www.deeplearning.ai/short-courses/ai-agents-in-langgraph,以下为代码的实现。 Basic ReAct Agent(manual action) import openai import re import httpx import os from dotenv import load_dotenv, find_dotenvOPENAI_API_KEY os.getenv(OPEN…...

window wsl安装ubuntu
文章目录 wsl安装ubuntu什么是wsl安装wsl检查运行 WSL 2 的要求将 WSL 2 设置为默认版本查看并安装linux WSL2的使用如何查看linux文件wsl如何使用代理:方法1:方法2:通过 DNS 隧道来配置 WSL 的网络 如何将 WSL 接入局域网并与宿主机同网段使用VScode连接…...
在同一域名下,传递消息给另一个页面)
postmessage()在同一域名下,传递消息给另一个页面
这里是同域名下,getmessage.html(发送信息)传递消息给index.html(收到信息,并回传收到信息) index.html页面 <!DOCTYPE html> <html><head><meta http-equiv"content-type"…...

初始redis:在Ubuntu上安装redis
1.先切换到root用户 使用su命令切换到root 2.使用apt命令来搜索redis相关的软件包 命令:apt search redis 3.下载redis 命令: apt install redis 在Ubuntu 20.04中 ,下载的redis版本是redis5 4.查看redis状态 命令: netst…...

生物素结合金纳米粒子(Bt@Au-NPs ) biotin-conjugated Au-NPs
一、定义与特点 定义:生物素结合金纳米粒子,简称BtAu-NPs或biotin-conjugated Au-NPs,是指通过特定的化学反应或物理方法将生物素修饰到金纳米粒子表面,形成稳定的纳米复合材料。 特点: 高稳定性:生物素的修…...

LeetCode热题100刷题9:25. K 个一组翻转链表、101. 对称二叉树、543. 二叉树的直径、102. 二叉树的层序遍历
25. K 个一组翻转链表 /*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), nex…...

PyJWT,一个基于JSON的轻量级安全通信方式的python库
目录 什么是JWT? JWT的构成 PyJWT库简介 安装PyJWT 生成JWT 验证JWT 使用PyJWT的高级功能 自定义Claims 错误处理 结语 什么是JWT? 在介绍PyJWT这个Python库之前,我们首先需要了解什么是JWT。JWT,全称JSON Web Token&am…...

Golang | Leetcode Golang题解之第223题矩形面积
题目: 题解: func computeArea(ax1, ay1, ax2, ay2, bx1, by1, bx2, by2 int) int {area1 : (ax2 - ax1) * (ay2 - ay1)area2 : (bx2 - bx1) * (by2 - by1)overlapWidth : min(ax2, bx2) - max(ax1, bx1)overlapHeight : min(ay2, by2) - max(ay1, by1)…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...

leetcode_69.x的平方根
题目如下 : 看到题 ,我们最原始的想法就是暴力解决: for(long long i 0;i<INT_MAX;i){if(i*ix){return i;}else if((i*i>x)&&((i-1)*(i-1)<x)){return i-1;}}我们直接开始遍历,我们是整数的平方根,所以我们分两…...
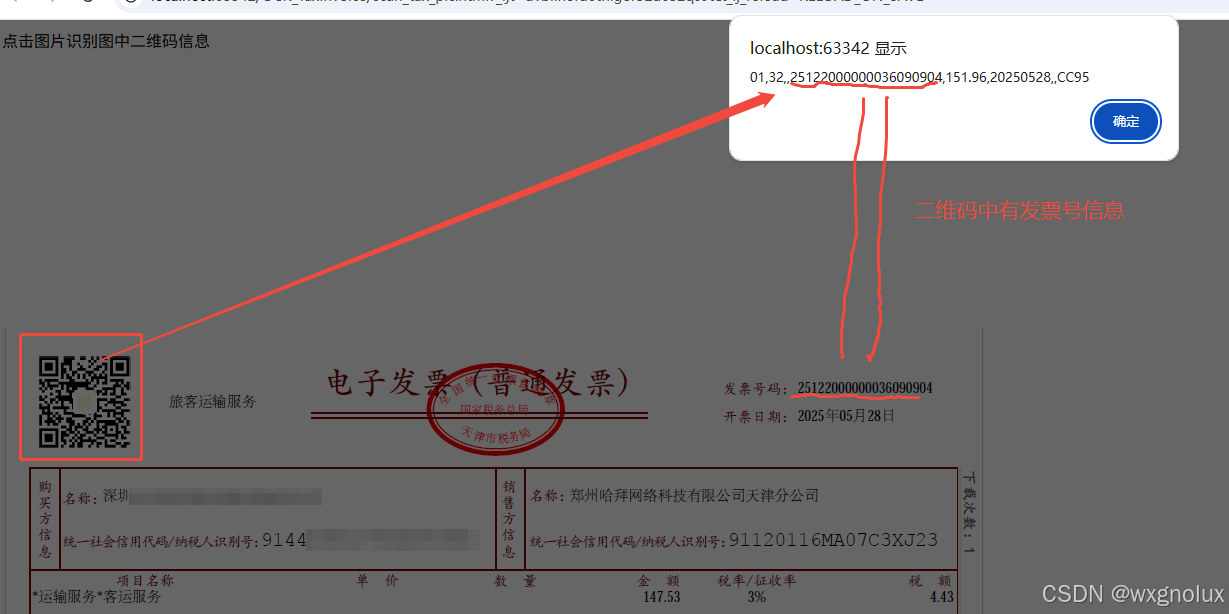
网页端 js 读取发票里的二维码信息(图片和PDF格式)
起因 为了实现在报销流程中,发票不能重用的限制,发票上传后,希望能读出发票号,并记录发票号已用,下次不再可用于报销。 基于上面的需求,研究了OCR 的方式和读PDF的方式,实际是可行的ÿ…...
