(三)前端javascript中的数据结构之集合
集合的特点
1.无序
2.唯一性
3.不可重复
集合相对于前面几种数据结构,比较简单好理解,看看代码实现就能知道他的用法了
集合的创建
function MySet() {this.item = {};
}
MySet.prototype.has = function (value) {return value in this.item;
};
//增
MySet.prototype.add = function (value) {if (this.has(value)) return false;this.item[value] = value;return true;
};
//删
MySet.prototype.remove = function (value) {if (!this.has(value)) return false;delete this.item[value];return true;
};
//清空
MySet.prototype.clear = function () {this.item = {};
};
//长度
MySet.prototype.size = function () {return Object.keys(this.item).length;
};
//获取值
MySet.prototype.values = function () {let arr = [];console.log("🚀 ~ Object.keys(this.item):", Object.keys(this.item));for (i = 0; i < Object.keys(this.item).length; i++) {const key = Object.keys(this.item)[i];arr.push(this.item[key]);}return arr;
};
//查询
MySet.prototype.print = function () {console.log(this.item);return this.item;
};
//集合的操作
//求并集
MySet.prototype.addUnion = function (data) {let newSet = new MySet();let values = this.values();for (let i = 0; i < values.length; i++) {newSet.add(values[i]);}let values2 = data.values();for (let i = 0; i < values2.length; i++) {newSet.add(values2[i]);}return newSet.values();
};
//求交集
MySet.prototype.interSection = function (data) {const interSection = new MySet();const oldValues = this.values();for (let i = 0; i < oldValues.length; i++) {if (data.has(oldValues[i])) {interSection.add(oldValues[i]);}}return interSection.values();
};
//求差集
MySet.prototype.diff = function (data) {const diff = new MySet();const oldValues = this.values();for (let i = 0; i < oldValues.length; i++) {if (!data.has(oldValues[i])) {diff.add(oldValues[i]);}}return diff.values();
};
测试
const set = new MySet()set.add('a',1)set.add('b',2)console.log(set.print())console.log('values',set.values())//测试求并集const set1 = new MySet()set1.add(1)set1.add(2)set1.add(3)const set2 = new MySet()set2.add(3)set2.add(4)set2.add(5)set2.add(6)set2.add(7)const result = set1.addUnion(set2)console.log(result) //[1, 2, 3, 4, 5, 6, 7]//求交集const set3 = new MySet()set3.add(1)set3.add(2)set3.add(3)const set4 = new MySet()set4.add(3)set4.add(4)set4.add(5)set4.add(6)const result2 = set3.interSection(set4)console.log("🚀 ~ result2:", result2)//求差集const set5 = new MySet()set5.add(1)set5.add(2)set5.add(3)const set6 = new MySet()set6.add(3)set6.add(4)const result3 = set5.diff(set6)console.log("🚀 ~ result3:", result3)
可以参照着练习下,其实不难,这个知识点!!
相关文章:

(三)前端javascript中的数据结构之集合
集合的特点 1.无序 2.唯一性 3.不可重复 集合相对于前面几种数据结构,比较简单好理解,看看代码实现就能知道他的用法了 集合的创建 function MySet() {this.item {}; } MySet.prototype.has function (value) {return value in this.item; };//增 M…...
VuePress 的更多配置
现在,读者应该对 VuePress、主题和插件等有了基本的认识,除了插件,VuePress 自身也有很多有用的配置,这里简单说明下。 VuePress 的介绍 在介绍了 VuePress 的基本使用、主题和插件的概念之后,我们再来看看官…...

问题解决|Python 代码的组织形式与编码规范
一、Python中组织形式 (一)组织形式(函数,类,模块,包,库)概览 (1)概览 组织形式描述特点或用途例子函数一段具有特定功能的代码块,可以接受参数…...

Flask项目搭建及部署 —— Python
flask搭建及部署 pip 19.2.3 python 3.7.5 Flask 1.1.1 Flask-SQLAlchemy 2.4.1 Pika 1.1.0 Redis 3.3.11 flask-wtf 0.14.2 1、创建flask项目: 创建完成后整个项目结构树: app.py: 项⽬管理⽂件,通过它管理项⽬。 static: 存放静态…...

【C++报错已解决】Invalid Use of ‘this’ Pointer
🎬 鸽芷咕:个人主页 🔥 个人专栏: 《C干货基地》《粉丝福利》 ⛺️生活的理想,就是为了理想的生活! 文章目录 引言 一、问题描述1.1 报错示例1.2 报错分析1.3 解决思路 二、解决方法2.1 方法一:修正‘this’指针使用2…...
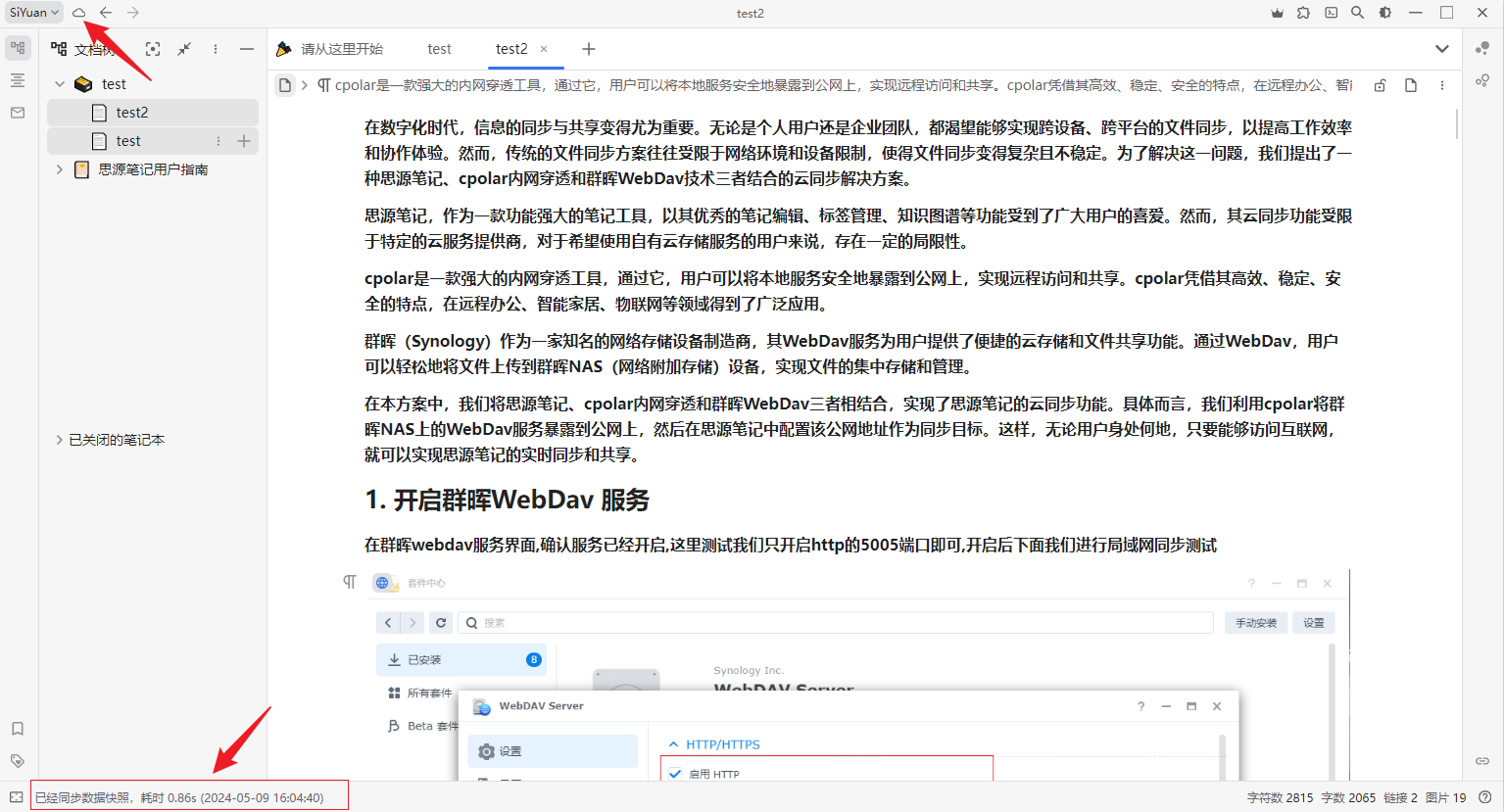
群晖NAS配置WebDav服务结合内网穿透实现跨平台云同步思源笔记
文章目录 前言1. 开启群晖WebDav 服务2. 本地局域网IP同步测试3. 群晖安装Cpolar4. 配置远程同步地址5. 笔记远程同步测试6. 固定公网地址7. 配置固定远程同步地址 前言 本教程主要分享如何将思源笔记、cpolar内网穿透和群晖WebDav三者相结合,实现思源笔记的云同步…...

内容监管与自由表达:Facebook的平衡之道
在当今数字化信息社会中,社交媒体平台不仅是人们交流和获取信息的主要渠道,也是自由表达的重要舞台。Facebook,作为全球最大的社交网络平台,连接了数十亿用户,形成了一个丰富多样的信息生态。然而,如何在维…...
电脑桌面日历记事本怎么弄 好用的桌面日历记事本
在这个数字化的时代,电脑已成为我们日常生活中不可或缺的伙伴。我常常在电脑上记录各种事项,以便随时查看和提醒自己。而我最钟爱的记事方式,莫过于使用桌面日历记事本。 想象一下,你的电脑桌面上有一个直观的日历,每…...

#招聘数据分析#2024年6月前程无忧招聘北上广深成渝对比情况
#招聘数据分析#2024年6月前程无忧招聘北上广深成渝对比情况 0、根据前程无忧不完全样本统计,北上广深成都重庆平均月工资从高到低依次为 北京15441元、上海14425元、深圳13310元、广州11192元、成都10539元、重庆10290。 1、成都招聘样本数全量35228个,…...

STM32 IIC详解(软件模拟)
目录 一、IIC协议基本原理 1.IIC协议概述 2.时序图分析 二、代码分析 1.IIC初始化 2.IIC起始信号 3.IIC发送数据 4.获取应答信号 5.读一个字节 6.产生ACK应答 7.不产生ACK应答 IIC(Inter-Integrated Circuit)在嵌入式系统中是一种常见的数据通…...

推三返一小程序商城开发搭建
推三返一小程序商城开发主要涉及到以下几个步骤: 确定需求和功能: 首先需要明确小程序商城的开发需求和功能。商家需要思考自己想要实现什么功能,例如推广、销售、裂变等。 同时还需要考虑小程序的页面设计、用户体验等方面。 选择合适的开…...

项目机会:4万平:智能仓,AGV,穿梭车,AMR,WMS,提升机,机器人……
导语 大家好,我是社长,老K。专注分享智能制造和智能仓储物流等内容。 如下为近期国内智能仓储物流相关项目的公开信息线索,这些项目具体信息会发布到知识星球,请感兴趣的球友先人一步到知识星球【智能仓储物流技术研习社】自行下载…...

[工具类]Java 合并、拆分PPT幻灯片
本文将介绍在Java程序中如何来合并及拆分PPT文档的方法。示例大纲: 1. 合并 1.1 将指定幻灯片合并到文档 1.2 合并多个幻灯片文档为一个文档 2. 拆分 2.1 按幻灯片每一页单独拆分为一个文档 2.2 按指定幻灯片页数范围来拆分为多个文档 使用工具:F…...

深入了解 Timber:全面掌握 Android 日志记录的最佳实践
深入了解 Timber:全面掌握 Android 日志记录的最佳实践 Timber 是由 Jake Wharton 提供的一个流行的 Android 日志记录库。它旨在简化日志记录、增强日志管理,并提高代码的可维护性。在本文中,我们将深入探讨 Timber 的功能、使用方法以及最…...

阿一课代表随堂分享:红队反向代理之使用frp搭建反向代理
frp反向代理 frp简介 frp 是一个开源、简洁易用、高性能的内网穿透和反向代理软件,支持 tcp, udp, http, https等协议。 frp 是一个可用于内网穿透的高性能的反向代理应用,分为服务端frps和客户端frpc,支持 tcp, udp, http, https 协议。详…...

基于vue的引入登录界面
以下是一些常见的登录页面布局: 1. 中心布局 - 登录表单位于页面的中心位置,通常包括用户名输入框、密码输入框、登录按钮等元素。页面背景简洁,以突出登录表单。 - 这种布局常见于大多数网站和应用,简洁明了,用户注意…...

centos7升级到欧拉openeule
centos7升级到欧拉openeule 一、准备工作 1、安装迁移工具(安装迁移工具的机器不能给自己升级,请用其他机器作为迁移母机) wget https://repo.oepkgs.net/openEuler/rpm/openEuler-20.03-LTS-SP1/contrib/x2openEuler/x86_64/Packages/x2…...

阿里云 Ubuntu 开启允许 ssh 密码方式登录
以前用的 centos,重置系统为 ubuntu 后在ssh 远程连接时遇到了点问题: 在阿里云控制台重置实例密码后无法使用密码进行 SSH 连接登录 原因:阿里云 Ubuntu 默认禁用密码登录方式 解决办法: 先使用其他用户登录到服务器 这里进来…...

利用投标相似度辅助围串标判定
摘要 围标(bid rigging)是一种非法的竞争行为,对市场公平性和公共资源分配造成严重影响。本文探讨了如何利用投标相似度来辅助判定围标行为。通过详细分析投标文件的内容相似性,选取适当的指标进行相似度计算,并结合实…...

iOS 开发者的 Flutter 入门课
作为一名 iOS 开发者,入门 Flutter 需要了解一些新的工具和概念,但也能利用你已有的知识和技能。以下是一个详细的入门指南,帮助你快速上手 Flutter: 1. 环境设置 首先,你需要设置开发环境。 安装 Flutter SDK 前往…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...
