C#用链表和数组分别实现堆栈
1.链表
实现栈的四个基本功能 入栈 出栈 长度 栈顶值
public class 基础 : MonoBehaviour
{public class MyStack{//定义每一个元素的数据结构 //下一个元素 和 该元素的值public class StackData{public StackData next;public object data;public StackData(StackData next, object data){this.next = next;this.data = data;}}//记录数量int size;//代表栈顶元素 StackData top;public void Push(object data){//因为栈是先进后出 后进来的元素就成为了栈顶//所以每压入一个元素 就让后进来元素的next指向前一个元素//出栈时 丢失最后节点的引用即可top = new StackData(top, data);size++;}public object Pop(){//弹出栈顶元素 同时下一个元素就是新栈顶object result = top.data;top = top.next;size--;return result;}public int Count{get{return size;}}public object Peek(){if (top == null) return null;return top.data;}}private void Start(){MyStack ms = new MyStack();ms.Push(1);ms.Push(2);ms.Push(3);ms.Push(4);ms.Push(5);Debug.Log(ms.Pop());Debug.Log(ms.Pop());Debug.Log(ms.Count);Debug.Log(ms.Peek());}
}
2.数组
(1)数组就是会更麻烦一点 不过可以加深对数组和栈的理解
(2)Pop和Enlarge 核心就是数组满了以后 创建一个新数组 将旧书组中的元素放入新数组 然后再将新数组赋值给旧数组即可
(3)栈是先进后出 所以只需要着重处理数组的末尾索引即可
public class 基础 : MonoBehaviour
{public class MyStack<T>{//通过数组实现堆栈public T[] list;public int maxSize = 2;public int nowSize = 0;public MyStack(){list = new T[maxSize];}public int Count {get{return nowSize;}}public void Push(T data){if(maxSize >= nowSize + 1){list[nowSize++] = data;}else{Enlarge();list[nowSize++] = data;}}public T Pop(){if(nowSize > 0){T[] list3 = new T[maxSize];T temp = list[--nowSize];for (int i = 0; i < list.Length - 1; i++){list3[i] = list[i];}list = list3;return temp;}else{return default(T);}}public void Enlarge(){T[] list2 = new T[maxSize * 2];for(int i = 0; i < list.Length; i++){list2[i] = list[i];}list = list2;maxSize *= 2;}}private void Start(){MyStack<int> ms = new MyStack<int>();ms.Push(1);ms.Push(2);ms.Push(3);ms.Push(4);ms.Push(5);Debug.Log(ms.Pop());Debug.Log(ms.Count);}
}
相关文章:

C#用链表和数组分别实现堆栈
1.链表 实现栈的四个基本功能 入栈 出栈 长度 栈顶值 public class 基础 : MonoBehaviour {public class MyStack{//定义每一个元素的数据结构 //下一个元素 和 该元素的值public class StackData{public StackData next;public object data;public StackData(StackData next,…...
原理)
【AI原理解析】—强化学习(RL)原理
目录 一、基本原理 二、基本框架与要素 三、学习过程 四、关键概念 五、算法实现 六、应用领域 七、总结 强化学习(Reinforcement Learning, RL) 一、基本原理 强化学习的基本原理是基于“试错学习”(trial-and-error learning&…...

java解析请求的字符串参数Content-Disposition: form-data;和拼接的键值对
项目场景: 获取到http请求的参数,已经被字符串接收了,需求是需要从字符串中解析出来。 一种情况是:Content-Disposition: form-data; name"userCode" 另一种是:key1value1&key2value2&key3value3…...

活动回顾|2024 MongoDB Developer Day圆满收官!
上周六,MongoDB专家与团队在深圳 与90位开发者度过了充实一日 至此,2024 MongoDB Developer Day 北上深三站之行全部圆满结束! 一文回顾本次活动全程与精彩影像! MongoDB Developer Day 专为开发者定制的技术盛宴 全天沉浸动手实…...

MySQL资源组的使用方法
MySQL支持创建和管理资源组,并允许将服务器内运行的线程分配给特定的组,以便线程根据组可用的资源执行。组属性允许控制其资源,以启用或限制组中线程的资源消耗。DBA可以针对不同的工作负载适当地修改这些属性。 目前,CPU时间是一…...

python--实验7 函数(1)
知识点 函数的定义与调用 函数分类:内置函数和自定义函数。函数定义:使用def关键字定义函数,包括函数名、参数列表和函数体。注意: (1)即使该函数不需要接收任何参数,也必须保留一对空的圆括号…...

【力扣】数组中的第K个最大元素
一、题目描述 给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。 请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。 你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。 示例 1: 输入: [3,2,1,5,…...
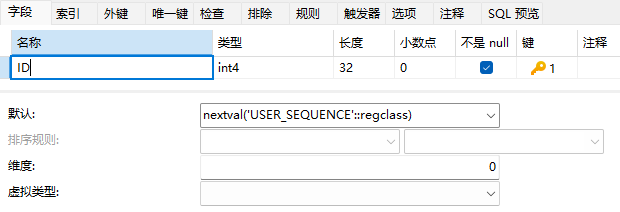
WTM的项目中EFCore如何适配人大金仓数据库
一、WTM是什么 WalkingTec.Mvvm框架(简称WTM)最早开发与2013年,基于Asp.net MVC3 和 最早的Entity Framework, 当初主要是为了解决公司内部开发效率低,代码风格不统一的问题。2017年9月,将代码移植到了.Net Core上&…...

互联网3.0时代的变革者:华贝甄选大模型创新之道
在当今竞争激烈的商业世界中,华贝甄选犹如一颗璀璨的明星,闪耀着独特的光芒。 华贝甄选始终将技术创新与研发视为发展的核心驱动力。拥有先进的研发团队和一流设施,积极探索人工智能、大数据、区块链等前沿技术,为用户提供高性能…...

Tomcat的安全配置
1、生产环境优化 2、部分漏洞修复 转载自风险评估:Tomcat的安全配置,Tomcat安全基线检查加固-CSDN博客...

[笔记] 卷积 - 01 变速箱需要放置多少个加速度传感器?
1.讨论范围 本帖主要对卷积运算的过程和物理意义进行基本的展开,不涉及具体的验算过程。 最终所要达成的目标是,能够自然地判断某种物理现象或者某个测量目标是否与卷积运算有关,以及如何进行测量,搜集数据,调用三方…...

Maya崩溃闪退常见原因及解决方案
Autodesk Maya 是一款功能强大的 3D 计算机图形程序,被电影、游戏和建筑等各个领域的设计师广泛使用。然而,Maya 就像任何其他软件一样可能会发生崩溃问题。在前文中,小编给大家介绍了3ds Max使用V-Ray渲染时的崩溃闪退解决方案: …...

编码与梦想:我的CSDN创作5周年
五年前的今天,我带着对技术的热爱和对知识的渴望,踏上了CSDN的创作之旅。这个平台对于我来说,不仅仅是一个分享和学习的场所,更是我成长和自我实现的见证。 机缘 记得那时,我正为了一个编程难题而苦恼,偶…...

Vue2 基础十Vuex
代码下载 Vuex 概述 组件之间共享数据的方式: 父组件向子组件传值,是以属性的形式绑定值到子组件(v-bind),然后子组件用属性props接收。子组件向父组件传值,子组件用 $emit() 自定义事件,父组…...

【大模型】驾驭未知领域:LLM如何处理域外或无意义的提示
驾驭未知领域:LLM如何处理域外或无意义的提示 引言一、概念解析1.1 域外提示1.2 无意义提示二、LLM处理策略2.1 上下文推断2.2 缺省回答2.3 模糊处理2.4 求助于常识三、实例对比3.1 域外提示实例3.2 无意义提示实例四、挑战与局限五、未来展望六、结语附录:术语解释与参考资料…...

Docker容器 为MySQL创建新用户和授权
当您需要为 MySQL 数据库创建一个新用户并配置其访问权限时,可以按照以下步骤操作。我将创建一个名为 newuser 的新用户,并为其授予在任何主机上访问所有数据库的权限。 创建新用户和授权步骤: 登录到 MySQL 服务器 首先,使用具有…...

openssh9.8p1更新 修复漏洞(CVE-2024-6387)
2024 年 7 月,互联网公开披露了一个 OpenSSH 的远程代码执行漏洞(CVE-2024-6387)。鉴于该漏洞虽然利用较为困难但危害较大,建议所有使用受影响的企业尽快修复该漏洞。 centos7 为例 yum -y install gcc make openssl-devel zlib…...
超市收银系统源码
今天给大家分享一套线上线下打通的收银系统,安卓/win双端线下收银台,可DIY、多模板的三端线上小程序商城,除此之外ERP进销存管理、商品管理、会员营销都很完善。 重点是系统支持OEM贴牌独立部署和全开源源码,非常适合一些正在寻找…...

word 使用手册
word 文档中如何将下行的指定文字退格到上行中 就像是这样的 编号:111 密码:222 编号:123 密码:321 编号:124 密码:331 变成 编号:111密码:222 编号:123密码࿱…...

vue学习day03-指令修饰符、v-bind对于样式控制的增强、v-model应用于其他表单元素
7、指令修饰符 (1)概念: 通过“.”指明一些指令后缀,不同后缀封装了不同的处理操作->简化代码 (2)按键修饰符 keyup.enter->键盘回车监听 (3)v-model修饰符 v-model.tri…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...
