来一场栈的大模拟(主要是单调栈)
一.栈模拟


二.单调栈求最大矩形面积

通常,直方图用于表示离散分布,例如,文本中字符的频率。
现在,请你计算在公共基线处对齐的直方图中最大矩形的面积。
图例右图显示了所描绘直方图的最大对齐矩形。
输入格式
输入包含几个测试用例。
每个测试用例占据一行,用以描述一个直方图,并以整数 n 开始,表示组成直方图的矩形数目。
然后跟随 n 个整数 h1,…,hn。
这些数字以从左到右的顺序表示直方图的各个矩形的高度。
每个矩形的宽度为 1。
同行数字用空格隔开。
当输入用例为 n=0 时,结束输入,且该用例不用考虑。
输出格式
对于每一个测试用例,输出一个整数,代表指定直方图中最大矩形的区域面积。
每个数据占一行。
请注意,此矩形必须在公共基线处对齐。
数据范围
1≤n≤100000
0≤hi≤1000000000
输入样例:
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0
输出样例:
8
4000
思考:这个题为什么可以用单调栈呢:
例如:栈中有1,4,6而这时来了一个3,你会发现有1和将要插入的3的时候这个4,6是用不着的,这是4和6就可以出栈,这不就是一个单调递增的栈吗?
代码:
#include<iostream>
#include<algorithm>using namespace std;const int N = 100010;//l[i], r[i]表示第i个矩形的高度可向两侧扩展的左右边界
int h[N], q[N], l[N], r[N];typedef long long ll;int main()
{int n;while(scanf("%d", &n), n){for(int i = 1; i <= n; i ++) scanf("%d", &h[i]);h[0] = h[n + 1] = -1;int tt = -1;q[++ tt] = 0;for(int i = 1; i <= n; i ++){while(h[q[tt]] >= h[i]) tt --;l[i] = q[tt]+1;q[++ tt] = i;}tt = -1;q[++ tt] = n + 1;for(int i = n; i; i --){while(h[q[tt]] >= h[i]) tt --;r[i] = q[tt]-1;q[++ tt] = i;}ll res = 0;for(int i = 1; i <= n; i ++) res = max(res,(ll)h[i]*(r[i]-l[i]+1));printf("%lld\n", res);}return 0;
} 


三.升级题
一.Maximal submatrix

代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=5e3+7;
int mp[maxn][maxn];
int mark[maxn][maxn];
int h[maxn];
int q[maxn];
int l[maxn];
int r[maxn];
int n,m;
int solve(int h[]){h[0]=h[m+1]=-1;int tt=-1;q[++tt]=0;for(int i=1;i<=m;i++){while(h[q[tt]]>=h[i]) tt--;l[i]=q[tt]+1;q[++tt]=i;}tt=-1;q[++tt]=m+1;for(int i=m;i;i--){while(h[q[tt]]>=h[i]) tt--;r[i]=q[tt]-1;q[++tt]=i;}int res=0;for(int i=1;i<=m;i++){res=max(res,h[i]*(r[i]-l[i]+1));}return res;
}
int main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t;cin>>t;while(t--){cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>mp[i][j];}}for(int j=1;j<=n;j++){mark[1][j]=1;for(int i=2;i<=n;i++){if(mp[i][j]>=mp[i-1][j]){mark[i][j]=mark[i-1][j]+1;}else{mark[i][j]=1;}}}int ans=0;for(int i=1;i<=n;i++){ans=max(ans,solve(mark[i]));}cout<<ans<<'\n';}system("pause");return 0;
}二. 与上题类似

这个题就是维护一个h[i][j]和l[i][j]和r[i][j],最后的答案就是max(h[i][j]*(r[i][j]-l[i][j]+1)),按上一道题做法也行。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=1e3+100;
char s[maxn][maxn];
int a[maxn][maxn];
int up[maxn][maxn];
int l[maxn][maxn];
int r[maxn][maxn];
int q[maxn];
int main(){int n,m;cin>>n>>m;for (int i = 1; i <= n; i ++ ){for(int j=1;j<=m;j++){cin>>s[i][j];if(s[i][j]=='F'){a[i][j]=1;}}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(a[i][j]){up[i][j]=up[i-1][j]+1;}else{up[i][j]=0;}}}for(int i=1;i<=n;i++){int tt=-1;up[i][0]=up[i][m+1]=-1;q[++tt]=0;for(int j=1;j<=m;j++){//维护单调递增的栈while(up[i][j]<=up[i][q[tt]]) tt--;l[i][j]=q[tt]+1;q[++tt]=j;}tt=-1;q[++tt]=m+1;for(int j=m;j>=1;j--){while(up[i][q[tt]]>=up[i][j]) tt--;r[i][j]=q[tt]-1;q[++tt]=j;}}int ans=0;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){//cout<<i<<" "<<j<<" "<<l[i][j]<<" "<<r[i][j]<<" "<<up[i][j]<<endl;ans=max(ans,(r[i][j]-l[i][j]+1)*up[i][j]);}}cout<<ans*3<<endl;
}三.移动列
给你一个二进制矩阵 matrix ,它的大小为 m x n ,你可以将 matrix 中的 列 按任意顺序重新排列。
请你返回最优方案下将 matrix 重新排列后,全是 1 的子矩阵面积。
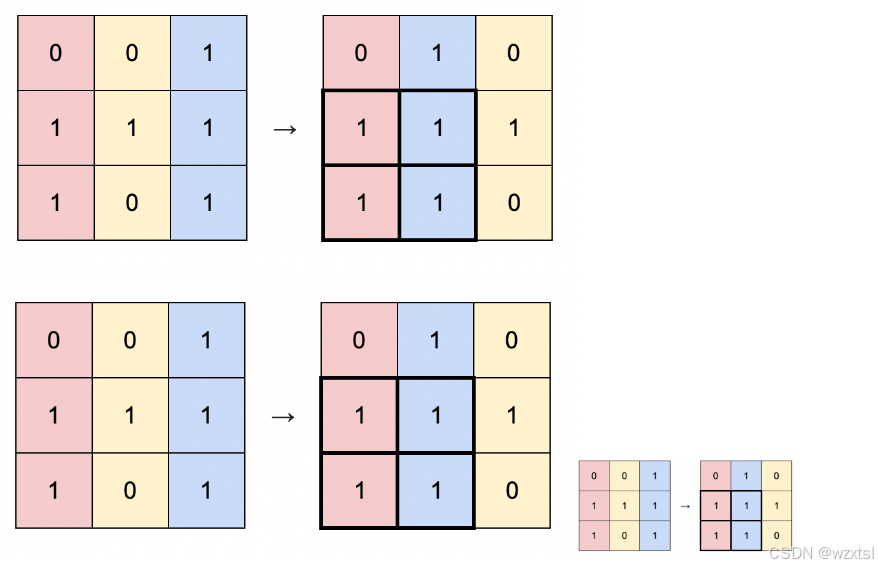
示例1:
输入:matrix = [[0,0,1],[1,1,1],[1,0,1]]
输出:4
解释:你可以按照上图方式重新排列矩阵的每一列。
最大的全 1 子矩阵是上图中加粗的部分,面积为 4 。
示例 2:
输入:matrix = [[1,0,1,0,1]]
输出:3
解释:你可以按照上图方式重新排列矩阵的每一列。
最大的全 1 子矩阵是上图中加粗的部分,面积为 3 。
示例 3:
输入:matrix = [[1,1,0],[1,0,1]]
输出:2
解释:由于你只能整列整列重新排布,所以没有比面积为 2 更大的全 1 子矩形。
示例 4:
输入:matrix = [[0,0],[0,0]]
输出:0
解释:由于矩阵中没有 1 ,没有任何全 1 的子矩阵,所以面积为 0 。
提示:
m == matrix.length
n == matrix[i].length
1 <= m * n <= 105
matrix[i][j] 要么是 0 ,要么是 1 。
这个题比上一个还简单就是维护一个h[i][j],他说可以交换任意列的次序,那么你在遍历每一列的时候拍个序就行;
class Solution {
public:int largestSubmatrix(vector<vector<int>>& w) {int n=w.size(),m=w[0].size();for(int i=1;i<n;i++){for(int j=0;j<m;j++){if(w[i][j]){w[i][j]+=w[i-1][j];}}}int ans=0;vector<int>q(m);for(int i=0;i<n;i++){for(int j=0;j<m;j++){q[j]=w[i][j];}sort(q.begin(),q.end(),greater<int>());for(int j=0;j<m;j++){ans=max(ans,q[j]*(j+1));}}return ans;}
};单调栈这一算法虽迟但到,完结撒花!!!
相关文章:

来一场栈的大模拟(主要是单调栈)
一.栈模拟 二.单调栈求最大矩形面积 通常,直方图用于表示离散分布,例如,文本中字符的频率。 现在,请你计算在公共基线处对齐的直方图中最大矩形的面积。 图例右图显示了所描绘直方图的最大对齐矩形。 输入格式 输入包含几个测…...
13 - matlab m_map地学绘图工具基础函数 - 介绍创建管理颜色映射的函数m_colmap和轮廓图绘制颜色条的函数m_contfbar
13 - matlab m_map地学绘图工具基础函数 - 介绍创建管理颜色映射的函数m_colmap和轮廓图绘制颜色条的函数m_contfbar 0. 引言1. 关于m_colmap2. 关于m_contfbar3. 结语 0. 引言 本篇介绍下m_map中用于创建和管理颜色映射函数(m_colmap)和 为轮廓图绘制颜…...
PTA - 编写函数计算圆面积
题目描述: 1.要求编写函数getCircleArea(r)计算给定半径r的圆面积,函数返回圆的面积。 2.要求编写函数get_rList(n) 输入n个值放入列表并将列表返回 函数接口定义: getCircleArea(r); get_rList(n); 传入的参数r表示圆的半径,…...

Golang | Leetcode Golang题解之第218题天际线问题
题目: 题解: type pair struct{ right, height int } type hp []pairfunc (h hp) Len() int { return len(h) } func (h hp) Less(i, j int) bool { return h[i].height > h[j].height } func (h hp) Swap(i, j int) { h[i], h[j]…...

【Mars3d】osgb倾斜摄影模型加载慢卡顿的优化方案参考
倾斜摄影模型文件一共6个多g,一个村子十几间房, 服务器配置:8c16g 100M 答: 目前可以对 3dtiles 模型有下面 3 方法来入手: 数据处理层面,比如数据处理工具的选择、和选择的工具本身的一些优化参数的设…...

认识同源策略
同源策略是一种浏览器安全机制,用于限制一个源的文档或脚本如何与另一个源的资源进行交互。源由协议(如HTTP或HTTPS)、域名和端口号组成。如果两个URL的协议、域名和端口都相同,则它们具有相同的源。 同源策略主要影响以下几个方…...

ADOQuery 查询MSSQL存储过程一个莫名其妙的错误;
在 SSMS 中执行完成正常的的存储过程。 也能正常的返回想要的数据,,然后通过 ADO 查询时,总是提法 某 字段不存在的问题; 此问题困扰了一天。 例如(当然,实际数据结构比下面举例的复杂)&…...

变阻器的分类
变阻器作为用于调节电路中电阻值的电子元件,在电子电路中具有广泛的应用。根据不同的工作原理和结构形式,变阻器可以分为多种类型。以下是对变阻器分类的详细阐述: 一、按工作原理分类 电位器是一种通过滑动端位置调节电阻值的变阻器&#x…...

微服务节流阀:Eureka中服务限流策略的精妙实现
微服务节流阀:Eureka中服务限流策略的精妙实现 引言 在微服务架构中,服务的稳定性和可靠性至关重要。限流策略作为保障服务稳定性的一种手段,通过控制服务的访问速率,可以有效避免服务过载和故障扩散。Eureka作为Netflix开源的服…...

Keras实战之图像分类识别
文章目录 整体流程数据加载与预处理搭建网络模型优化网络模型学习率Drop-out操作权重初始化方法对比正则化加载模型进行测试 实战:利用Keras框架搭建神经网络模型实现基本图像分类识别,使用自己的数据集进行训练测试。 问:为什么选择Keras&am…...

Celery,一个实时处理的 Python 分布式系统
大家好!我是爱摸鱼的小鸿,关注我,收看每期的编程干货。 一个简单的库,也许能够开启我们的智慧之门, 一个普通的方法,也许能在危急时刻挽救我们于水深火热, 一个新颖的思维方式,也许能…...

源码编译安装 LAMP
源码编译安装 LAMP Apache 网站服务基础Apache 简介安装 httpd 服务器 httpd 服务器的基本配置Web 站点的部署过程httpd.conf 配置文件 构建虚拟 Web 主机基于域名的虚拟主机基于IP 地址、基于端口的虚拟主机 MySQL 的编译安装构建 PHP 运行环境安装PHP软件包设置 LAMP 组件环境…...
PostgreSQL的pg_filedump工具
PostgreSQL的pg_filedump工具 基础信息 OS版本:Red Hat Enterprise Linux Server release 7.9 (Maipo) DB版本:16.2 pg软件目录:/home/pg16/soft pg数据目录:/home/pg16/data 端口:5777pg_filedump 是一个工具&#x…...

Java语言+后端+前端Vue,ElementUI 数字化产科管理平台 产科电子病历系统源码
Java语言后端前端Vue,ElementUI 数字化产科管理平台 产科电子病历系统源码 Java开发的数字化产科管理系统,已在多家医院实施,支持直接部署。系统涵盖孕产全程,包括门诊、住院、统计和移动服务,整合高危管理、智能提醒、档案追踪等…...

Linux 服务器环境搭建
一、安装 JDK 官网下载地址:https://www.oracle.com/java/technologies/downloads # 创建目录 mkdir /usr/local/java/# 解压 tar -zxvf jdk-8u333-linux-x64.tar.gz -C /usr/local/java/# 配置环境变量 vim /etc/profileexport export JAVA_HOME/usr/local/java/…...
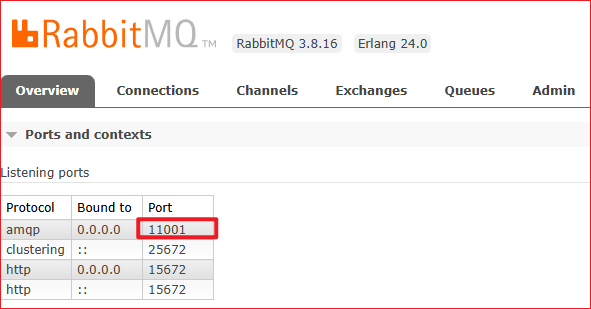
RabbitMQ 更改服务端口号
需求 windows环境下,将RabbitMQ默认的端口号 5672 改为 11001 实现 本机RabbitMQ版本为3.8.16,找到配置文件位置,路径为:C:\Users\%USERNAME%\AppData\Roaming\RabbitMQ\advanced.config 配置文件默认内容为空 填写修改端口号…...

16:9横屏短视频素材库有哪些?横屏短视频素材网站分享
在这个视觉内容至关重要的时代,16:9横屏视频因其宽广的画面和优越的观赏体验,已经成为无数创作者和营销专家的首选格式。但要创造出吸引人的横屏视频,高质量的视频素材库是不可或缺的。不管你是资深视频制作人还是刚入行的新手,下…...

在Java中,创建一个实现了Callable接口的类可以提供强大的灵活性,特别是当你需要在多线程环境中执行任务并获取返回结果时。
在Java中,创建一个实现了Callable接口的类可以提供强大的灵活性,特别是当你需要在多线程环境中执行任务并获取返回结果时。以下是一个简单的案例,演示了如何创建一个实现了Callable接口的类,并在线程池中执行它。 首先࿰…...

Vuforia AR篇(八)— AR塔防上篇
目录 前言一、设置Vuforia AR环境1. 添加AR Camera2. 设置目标图像 二、创建塔防游戏基础1. 导入素材2. 搭建场景3. 创建敌人4. 创建脚本 前言 在增强现实(AR)技术快速发展的今天,Vuforia作为一个强大的AR开发平台,为开发者提供了…...
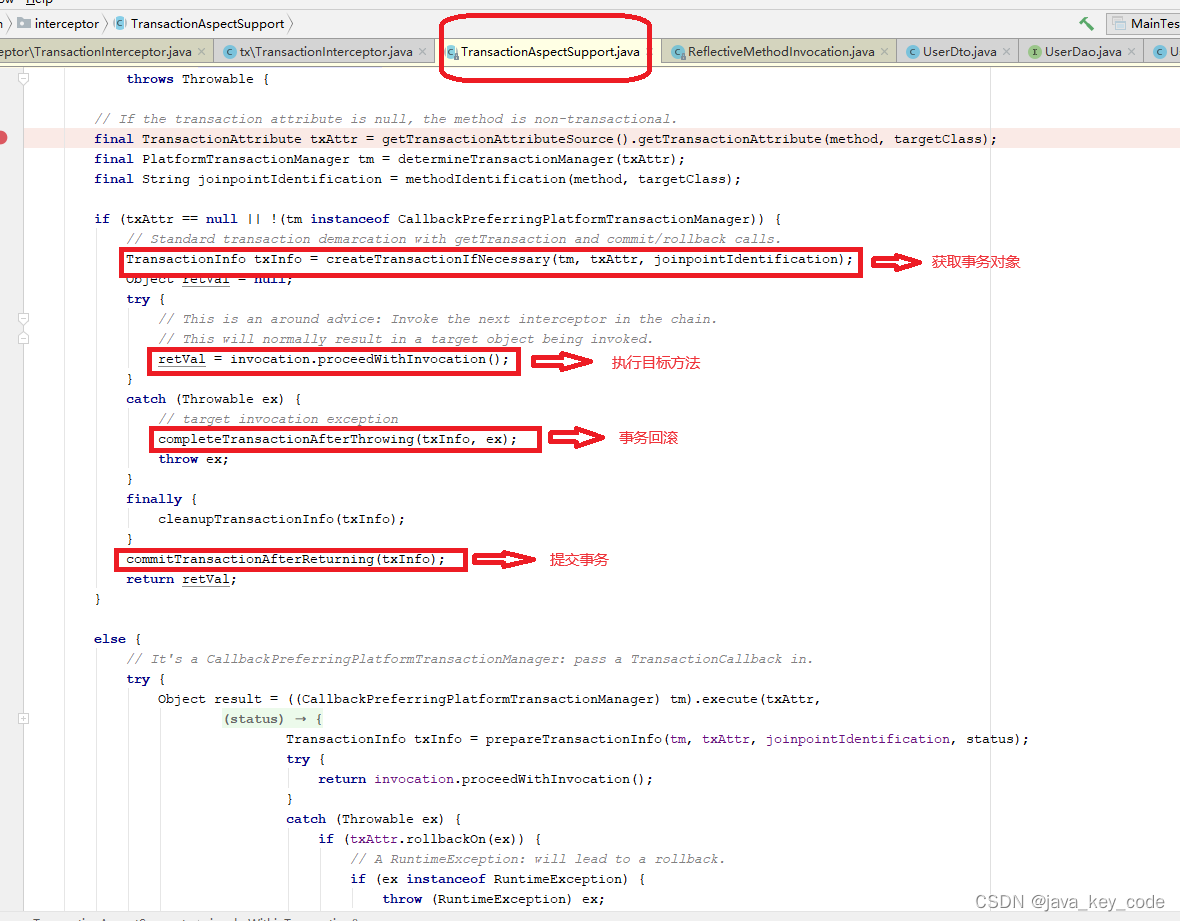
Spring AOP源码篇四之 数据库事务
了解了Spring AOP执行过程,再看Spring事务源码其实非常简单。 首先从简单使用开始, 演示Spring事务使用过程 Xml配置: <?xml version"1.0" encoding"UTF-8"?> <beans xmlns"http://www.springframework.org/schema…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...
