第16章 主成分分析:四个案例及课后习题
1.假设 x x x为 m m m 维随机变量,其均值为 μ \mu μ,协方差矩阵为 Σ \Sigma Σ。
考虑由 m m m维随机变量 x x x到 m m m维随机变量 y y y的线性变换
y i = α i T x = ∑ k = 1 m α k i x k , i = 1 , 2 , ⋯ , m y _ { i } = \alpha _ { i } ^ { T } x = \sum _ { k = 1 } ^ { m } \alpha _ { k i } x _ { k } , \quad i = 1,2 , \cdots , m yi=αiTx=k=1∑mαkixk,i=1,2,⋯,m
其中 α i T = ( α 1 i , α 2 i , ⋯ , α m i ) \alpha _ { i } ^ { T } = ( \alpha _ { 1 i } , \alpha _ { 2 i } , \cdots , \alpha _ { m i } ) αiT=(α1i,α2i,⋯,αmi)。
如果该线性变换满足以下条件,则称之为总体主成分:
(1) α i T α i = 1 , i = 1 , 2 , ⋯ , m \alpha _ { i } ^ { T } \alpha _ { i } = 1 , i = 1,2 , \cdots , m αiTαi=1,i=1,2,⋯,m;
(2) cov ( y i , y j ) = 0 ( i ≠ j ) \operatorname { cov } ( y _ { i } , y _ { j } ) = 0 ( i \neq j ) cov(yi,yj)=0(i=j);
(3)变量 y 1 y_1 y1是 x x x的所有线性变换中方差最大的; y 2 y_2 y2是与 y 1 y_1 y1不相关的 x x x的所有线性变换中方差最大的;一般地, y i y_i yi是与 y 1 , y 2 , ⋯ , y i − 1 , ( i = 1 , 2 , ⋯ , m ) y _ { 1 } , y _ { 2 } , \cdots , y _ { i - 1 } , ( i = 1,2 , \cdots , m ) y1,y2,⋯,yi−1,(i=1,2,⋯,m)都不相关的 x x x的所有线性变换中方差最大的;这时分别称 y 1 , y 2 , ⋯ , y m y _ { 1 } , y _ { 2 } , \cdots , y _ { m } y1,y2,⋯,ym为 x x x的第一主成分、第二主成分、…、第 m m m主成分。
2.假设 x x x是 m m m维随机变量,其协方差矩阵是 Σ \Sigma Σ, Σ \Sigma Σ的特征值分别是 λ 1 ≥ λ 2 ≥ ⋯ ≥ λ m ≥ 0 \lambda _ { 1 } \geq\lambda _ { 2 } \geq \cdots \geq \lambda _ { m } \geq 0 λ1≥λ2≥⋯≥λm≥0,特征值对应的单位特征向量分别是 α 1 , α 2 , ⋯ , α m \alpha _ { 1 } , \alpha _ { 2 } , \cdots , \alpha _ { m } α1,α2,⋯,αm,则 x x x的第2主成分可以写作
y i = α i T x = ∑ k = 1 m α k i x k , i = 1 , 2 , ⋯ , m y _ { i } = \alpha _ { i } ^ { T } x = \sum _ { k = 1 } ^ { m } \alpha _ { k i } x _ { k } , \quad i = 1,2 , \cdots , m yi=αiTx=k=1∑mαkixk,i=1,2,⋯,m
并且, x x x的第 i i i主成分的方差是协方差矩阵 Σ \Sigma Σ的第 i i i个特征值,即 var ( y i ) = α i T Σ α i = λ i \operatorname { var } ( y _ { i } ) = \alpha _ { i } ^ { T } \Sigma \alpha _ { i } = \lambda _ { i } var(yi)=αiTΣαi=λi
3.主成分有以下性质:
主成分 y y y的协方差矩阵是对角矩阵 cov ( y ) = Λ = diag ( λ 1 , λ 2 , ⋯ , λ m ) \operatorname { cov } ( y ) = \Lambda = \operatorname { diag } ( \lambda _ { 1 } , \lambda _ { 2 } , \cdots , \lambda _ { m } ) cov(y)=Λ=diag(λ1,λ2,⋯,λm)
主成分 y y y的方差之和等于随机变量 x x x的方差之和
∑ i = 1 m λ i = ∑ i = 1 m σ i i \sum _ { i = 1 } ^ { m } \lambda _ { i } = \sum _ { i = 1 } ^ { m } \sigma _ { i i } i=1∑mλi=i=1∑mσii
其中 σ i i \sigma _ { i i } σii是 x 2 x_2 x2的方差,即协方差矩阵 Σ \Sigma Σ的对角线元素。
主成分 y k y_k yk与变量 x 2 x_2 x2的相关系数 ρ ( y k , x i ) \rho ( y _ { k } , x _ { i } ) ρ(yk,xi)称为因子负荷量(factor loading),它表示第 k k k个主成分 y k y_k yk与变量 x x x的相关关系,即 y k y_k yk对 x x x的贡献程度。
ρ ( y k , x i ) = λ k α i k σ i i , k , i = 1 , 2 , ⋯ , m \rho ( y _ { k } , x _ { i } ) = \frac { \sqrt { \lambda _ { k } } \alpha _ { i k } } { \sqrt { \sigma _ { i i } } } , \quad k , i = 1,2 , \cdots , m ρ(yk,xi)=σiiλkαik,k,i=1,2,⋯,m
4.样本主成分分析就是基于样本协方差矩阵的主成分分析。
给定样本矩阵
X = [ x 1 x 2 ⋯ x n ] = [ x 11 x 12 ⋯ x 1 n x 21 x 22 ⋯ x 2 n ⋮ ⋮ ⋮ x m 1 x m 2 ⋯ x m n ] X = \left[ \begin{array} { l l l l } { x _ { 1 } } & { x _ { 2 } } & { \cdots } & { x _ { n } } \end{array} \right] = \left[ \begin{array} { c c c c } { x _ { 11 } } & { x _ { 12 } } & { \cdots } & { x _ { 1 n } } \\ { x _ { 21 } } & { x _ { 22 } } & { \cdots } & { x _ { 2 n } } \\ { \vdots } & { \vdots } & { } & { \vdots } \\ { x _ { m 1 } } & { x _ { m 2 } } & { \cdots } & { x _ { m n } } \end{array} \right] X=[x1x2⋯xn]= x11x21⋮xm1x12x22⋮xm2⋯⋯⋯x1nx2n⋮xmn
其中 x j = ( x 1 j , x 2 j , ⋯ , x m j ) T x _ { j } = ( x _ { 1 j } , x _ { 2 j } , \cdots , x _ { m j } ) ^ { T } xj=(x1j,x2j,⋯,xmj)T是 x x x的第 j j j个独立观测样本, j = 1 , 2 , … , n j=1,2,…,n j=1,2,…,n。
X X X的样本协方差矩阵
S = [ s i j ] m × m , s i j = 1 n − 1 ∑ k = 1 n ( x i k − x ‾ i ) ( x j k − x ‾ j ) i = 1 , 2 , ⋯ , m , j = 1 , 2 , ⋯ , m \left. \begin{array} { c } { S = [ s _ { i j } ] _ { m \times m } , \quad s _ { i j } = \frac { 1 } { n - 1 } \sum _ { k = 1 } ^ { n } ( x _ { i k } - \overline { x } _ { i } ) ( x _ { j k } - \overline { x } _ { j } ) } \\ { i = 1,2 , \cdots , m , \quad j = 1,2 , \cdots , m } \end{array} \right. S=[sij]m×m,sij=n−11∑k=1n(xik−xi)(xjk−xj)i=1,2,⋯,m,j=1,2,⋯,m
给定样本数据矩阵 X X X,考虑向量 x x x到 y y y的线性变换 y = A T x y = A ^ { T } x y=ATx
这里
A = [ a 1 a 2 ⋯ a m ] = [ a 11 a 12 ⋯ a 1 m a 21 a 22 ⋯ a 2 m ⋮ ⋮ ⋮ a m 1 a m 2 ⋯ a m m ] A = \left[ \begin{array} { l l l l } { a _ { 1 } } & { a _ { 2 } } & { \cdots } & { a _ { m } } \end{array} \right] = \left[ \begin{array} { c c c c } { a _ { 11 } } & { a _ { 12 } } & { \cdots } & { a _ { 1 m } } \\ { a _ { 21 } } & { a _ { 22 } } & { \cdots } & { a _ { 2 m } } \\ { \vdots } & { \vdots } & { } & { \vdots } \\ { a _ { m 1 } } & { a _ { m 2 } } & { \cdots } & { a _ { m m } } \end{array} \right] A=[a1a2⋯am]= a11a21⋮am1a12a22⋮am2⋯⋯⋯a1ma2m⋮amm
如果该线性变换满足以下条件,则称之为样本主成分。样本第一主成分 y 1 = a 1 T x y _ { 1 } = a _ { 1 } ^ { T } x y1=a1Tx是在 a 1 T a 1 = 1 a _ { 1 } ^ { T } a _ { 1 } = 1 a1Ta1=1条件下,使得 a 1 T x j ( j = 1 , 2 , ⋯ , n ) a _ { 1 } ^ { T } x _ { j } ( j = 1,2 , \cdots , n ) a1Txj(j=1,2,⋯,n)的样本方差 a 1 T S a 1 a _ { 1 } ^ { T } S a _ { 1 } a1TSa1最大的 x x x的线性变换;
样本第二主成分 y 2 = a 2 T x y _ { 2 } = a _ { 2 } ^ { T } x y2=a2Tx是在 a 2 T a 2 = 1 a _ { 2 } ^ { T } a _ { 2 } = 1 a2Ta2=1和 a 2 T x j a _ { 2 } ^ { T } x _ { j } a2Txj与 a 1 T x j ( j = 1 , 2 , ⋯ , n ) a _ { 1 } ^ { T } x _ { j } ( j = 1,2 , \cdots , n ) a1Txj(j=1,2,⋯,n)的样本协方差 a 1 T S a 2 = 0 a _ { 1 } ^ { T } S a _ { 2 } = 0 a1TSa2=0条件下,使得 a 2 T x j ( j = 1 , 2 , ⋯ , n ) a _ { 2 } ^ { T } x _ { j } ( j = 1,2 , \cdots , n ) a2Txj(j=1,2,⋯,n)的样本方差 a 2 T S a 2 a _ { 2 } ^ { T } S a _ { 2 } a2TSa2最大的 x x x的线性变换;
一般地,样本第 i i i主成分 y i = a i T x y _ { i } = a _ { i } ^ { T } x yi=aiTx是在 a i T a i = 1 a _ { i } ^ { T } a _ { i } = 1 aiTai=1和 a i T x j a _ { i } ^ { T } x _ { j } aiTxj与 a k T x j ( k < i , j = 1 , 2 , ⋯ , n ) a _ { k } ^ { T } x _ { j } ( k < i , j = 1,2 , \cdots , n ) akTxj(k<i,j=1,2,⋯,n)的样本协方差 a k T S a i = 0 a _ { k } ^ { T } S a _ { i } = 0 akTSai=0条件下,使得 a i T x j ( j = 1 , 2 , ⋯ , n ) a _ { i } ^ { T } x _ { j } ( j = 1,2 , \cdots , n ) aiTxj(j=1,2,⋯,n)的样本方差 a k T S a i a _ { k } ^ { T } S a _ { i } akTSai最大的 x x x的线性变换。
5.主成分分析方法主要有两种,可以通过相关矩阵的特征值分解或样本矩阵的奇异值分解进行。
(1)相关矩阵的特征值分解算法。针对 m × n m \times n m×n样本矩阵 X X X,求样本相关矩阵
R = 1 n − 1 X X T R = \frac { 1 } { n - 1 } X X ^ { T } R=n−11XXT
再求样本相关矩阵的 k k k个特征值和对应的单位特征向量,构造正交矩阵
V = ( v 1 , v 2 , ⋯ , v k ) V = ( v _ { 1 } , v _ { 2 } , \cdots , v _ { k } ) V=(v1,v2,⋯,vk)
V V V的每一列对应一个主成分,得到 k × n k \times n k×n样本主成分矩阵
Y = V T X Y = V ^ { T } X Y=VTX
(2)矩阵 X X X的奇异值分解算法。针对 m × n m \times n m×n样本矩阵 X X X
X ′ = 1 n − 1 X T X ^ { \prime } = \frac { 1 } { \sqrt { n - 1 } } X ^ { T } X′=n−11XT
对矩阵 X ′ X ^ { \prime } X′进行截断奇异值分解,保留 k k k个奇异值、奇异向量,得到
X ′ = U S V T X ^ { \prime } = U S V ^ { T } X′=USVT
V V V的每一列对应一个主成分,得到 k × n k \times n k×n样本主成分矩阵 Y Y Y
Y = V T X Y = V ^ { T } X Y=VTX
案例1:高维数据的可视化
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
from matplotlib_inline import backend_inlinebackend_inline.set_matplotlib_formats('svg')iris = load_iris()
X = iris.data # 形状(150,4)
y = iris.targetpca = PCA(n_components=2)
X_dr = pca.fit_transform(X)
# print(X_dr) # 形状(150,2)colors = ['red', 'black', 'orange']
plt.figure()
for i in range(3):plt.scatter(X_dr[y == i, 0],X_dr[y == i, 1],c=colors[i],alpha=0.7,label=iris.target_names[i])
plt.legend()
plt.title('PCA of IRIS dataset')
plt.show()# 一些关键信息
print('各主成分的方差(即协方差矩阵的特征值):', pca.explained_variance_, '\n特征向量:',pca.components_, '\n可解释性方差贡献率:', pca.explained_variance_ratio_,'\n保留了原数据多少信息(累计方差贡献率):', pca.explained_variance_ratio_.sum())

各主成分的方差(即协方差矩阵的特征值): [4.22824171 0.24267075]
特征向量: [[ 0.36138659 -0.08452251 0.85667061 0.3582892 ][ 0.65658877 0.73016143 -0.17337266 -0.07548102]]
可解释性方差贡献率: [0.92461872 0.05306648]
保留了原数据多少信息(累计方差贡献率): 0.977685206318795
接下来说明选择主成分个数(n_components)的一些方法
# 法一:选择累计方差贡献率曲线的突然变平坦的点对应的主成分个数
pca_ = PCA(n_components=4).fit(X)
plt.plot(range(1, 5), np.cumsum(pca_.explained_variance_ratio_))
plt.xticks([1, 2, 3, 4])
plt.show() # 故选择主成分个数为2较合适

# 法二:令n_components='mle'使用极大似然估计 自动选择主成分个数
pca_mle = PCA(n_components='mle').fit(X)
X_mle = pca_mle.fit_transform(X)
print(X_mle.shape, pca_mle.explained_variance_ratio_.sum())
# 可以看出这种方法选择主成分的个数为3
(150, 3) 0.9947878161267247
# 法三:输出浮点数n_components=0.9按信息量占比选择主成分个数
# 确保选择的主成分能够解释至少 97% 的数据方差,并使用 完全SVD方法 进行计算
pca_3 = PCA(n_components=0.97, svd_solver="full").fit(X)
X_3 = pca_3.fit_transform(X)
print(X_3.shape, pca_3.explained_variance_ratio_.sum()) # 选择两个主成分个数就能包含原数据信息97%以上了
(150, 2) 0.977685206318795
svd_solver 参数决定了计算主成分的奇异值分解 (SVD) 方法。以下是 svd_solver 参数的可选值及其含义:
- auto:默认值。根据输入数据的大小和所需的主成分数量,自动选择合适的 SVD 方法。
- full:使用标准的完全 SVD 方法。这种方法比较慢,但适用于所有情况,特别是当数据矩阵的形状为 n_samples > n_features 或 n_features > n_samples 时。
- arpack:使用 scipy.sparse.linalg.svds 实现的截断 SVD。这种方法适合计算少数几个主成分的情况,特别是当所需的主成分数远小于数据矩阵的形状时。
- randomized:使用随机 SVD 方法,适用于大数据集,且需要计算的主成分数不多的情况。这种方法通常比完全 SVD 方法快很多。
案例2:人脸识别
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import fetch_lfw_people
from matplotlib_inline import backend_inline# 设置 matplotlib 的显示格式为 SVG 矢量图
backend_inline.set_matplotlib_formats('svg')# 获取 LFW (Labeled Faces in the Wild) 数据集
faces = fetch_lfw_people(min_faces_per_person=60)
# 数据集包含每个人至少 60 张脸部图像# 查看数据集的形状
# print(faces.images.shape) # (1348, 62, 47)
# 62 是每个图像的行数,47 是每个图像的列数,因此每个图像有 62*47 = 2914 个像素
# 数据集中共有 1348 张图像# print(faces.data.shape) # (1348, 2914)
# 数据集的形状为 (1348, 2914),表示有 1348 个样本,每个样本有 2914 个特征(像素值)# 创建图像网格,显示前 24 张图像,每个子图不显示坐标轴刻度
fig, axes = plt.subplots(3, 8, figsize=(8, 4), subplot_kw={"xticks": [], "yticks": []})
for i, ax in enumerate(axes.flat): # axes 是一个 3x8 的数组,包含了 24 个 AxesSubplot 对象。axes.flat 将其展开为一个一维数组ax.imshow(faces.images[i, :, :], cmap='gray') # 获取第 i 张图像,这是一张 2D 数组(灰度图像)plt.show()

# 原本有2914维,现在试着降到200维# 将数据矩阵 X 定义为 faces 数据集的 data 属性
X = faces.data # # (1348, 2914)
pca_face = PCA(n_components=200).fit(X)
X_face=pca_face.fit_transform(X) # (1384,200)
V = pca_face.components_
print('奇异值分解中的V的形状(即特征矩阵):', V.shape, '\n200个主成分保留了原数据多少信息(累计方差贡献率):',pca_face.explained_variance_ratio_.sum())fig, axes = plt.subplots(3, 8, figsize=(8, 4), subplot_kw={"xticks": [], "yticks": []})
for i, ax in enumerate(axes.flat): ax.imshow(V[i, :].reshape(62,47), cmap='gray') # 可见第一主成分(第一张图)获取的是人的轮廓信息,其他主成分不好解释……# 使用inverse_transform可以逆转回去(但这种逆转不是完全可逆的,毕竟降维时只使用了200个主成分)
X_inv=pca_face.inverse_transform(X_face)# 可视化逆转回的数据
fig, ax = plt.subplots(2, 8, figsize=(8, 2.5), subplot_kw={"xticks": [], "yticks": []})
# 现在的ax中是2行8列,作为对比:第一行是原数据,第二行是inverse_transform后返回的数据
# 一次循环画同一列上的两张图,而不是把ax拉平
for i in range(8):ax[0, i].imshow(faces.images[i, :, :], cmap="binary_r")ax[1, i].imshow(X_inv[i].reshape(62, 47), cmap="binary_r")
plt.show()
奇异值分解中的V的形状(即特征矩阵): (200, 2914)
200个主成分保留了原数据多少信息(累计方差贡献率): 0.9420423


案例3:用PCA做噪音过滤(手写数字识别)
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as npdigits = load_digits()
# digits.data.shape # (1797,64)# 定义一个画图的函数
def plot_digits(data):fig, axes = plt.subplots(4, 10, figsize=(10, 4), subplot_kw={"xticks": [], "yticks": []})for i, ax in enumerate(axes.flat):ax.imshow(data[i].reshape(8, 8), cmap="binary")plt.show()plot_digits(digits.data)

# 将均值为0、标准差为2的正态分布随机数添加到 digits.data 中,从而人为创建一个带有噪声的新数据集 noisy
np.random.RandomState(42)
noisy = np.random.normal(digits.data, 2)
plot_digits(noisy)

# 利用PCA的inverse_transform函数去噪
pca_digits = PCA(n_components=0.7, svd_solver="full").fit(noisy)
noisy_ = pca_digits.fit_transform(noisy)
no_noisy_data = pca_digits.inverse_transform(noisy_)
plot_digits(no_noisy_data)

案例4:手写数字识别
对于某些算法,如果数据维度过大那么运行时间将会非常久,例如KNN。故利用PCA把原数据进行降维后再运用其他算法进行后续工作是常见的做法。本处案例进行手写数字识别。
from sklearn.decomposition import PCA
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.neighbors import KNeighborsClassifier as KNN
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
import pandas as pd
import numpy as npplt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的负号的乱码问题data = pd.read_csv("D:/PycharmProjects/ML20230605/机器学习/3、数据预处理与特征工程/digit recognizor.csv")
X = data.iloc[:, 1:] # (42000,784)
y = data.iloc[:, 0]# 选择主成分个数,先设置200观察一下图像
pca_line = PCA(n_components=200).fit(X)
plt.figure(figsize=[20, 5])
plt.plot(np.cumsum(pca_line.explained_variance_ratio_))
plt.xlabel("主成分个数")
plt.ylabel("累计方差贡献率")
plt.show()

# 看图,缩小主成分范围。使用随机森林和KNN建模
# score_r = []
score_knn = []
for i in range(25, 30):X_dr = PCA(n_components = i).fit_transform(X)
# once_r = cross_val_score(RFC(n_estimators=10, random_state=0), X_dr, y, cv=5).mean()once_knn = cross_val_score(KNN(), X_dr, y, cv=5).mean()
# score_r.append(once_r)score_knn.append(once_knn)
plt.figure(figsize=[20, 5])
# plt.plot(range(25, 30), score_r)
plt.plot(range(25, 30), score_knn)
plt.show() # 于是选择29作为主成分个数

X_dr=PCA(n_components=29).fit_transform(X)
print(cross_val_score(KNN(), X_dr, y, cv=5).mean()) # KNN未进行任何调参时# 对KNN模型进行调参
score = []
for i in range(3,10):once = cross_val_score(KNN(i), X_dr, y, cv=5).mean()score.append(once)
plt.figure(figsize=[20, 5])
plt.plot(range(3,10), score)
plt.show() # 发现K=5时准确率最高,其实这就是KNN的默认参数
0.9720952380952381

习题

16.1
import numpy as np
from sklearn.decomposition import PCA# 定义数据矩阵
X = np.array([[2, 3, 3, 4, 5, 7], [2, 4, 5, 5, 6, 8]])
X = X.astype("float64")# 规范化变量
avg = np.average(X, axis=1)
var = np.var(X, axis=1)
for i in range(X.shape[0]):X[i] = (X[i, :] - avg[i]) / np.sqrt(var[i])# 使用PCA类
pca = PCA(n_components=2)# 拟合数据并转换
X_pca = pca.fit_transform(X.T)# 打印结果
print("特征向量 V:\n", pca.components_.T) # pca.components_ 属性返回的是形状为 (n_components, n_features) 的矩阵
print("样本主成分矩阵 Y:\n", X_pca.T)# 使用自定义的pca_svd函数
def pca_svd(X, k):"""样本矩阵的奇异值分解的主成分分析算法:param X: 样本矩阵X:param k: 主成分个数k:return: 特征向量V,样本主成分矩阵Y"""n_samples = X.shape[1] # 这里的X矩阵的一列表示一个观测# 构造新的n×m矩阵T = X.T / np.sqrt(n_samples - 1)# 对矩阵T进行截断奇异值分解U, S, Vt = np.linalg.svd(T)V = Vt.T[:, :k]# 求k×n的样本主成分矩阵return V, np.dot(V.T, X)# 设置精度为3
np.set_printoptions(precision=3, suppress=True)
V, vnk = pca_svd(X, 2)print("正交矩阵V:")
print(V)
print("样本主成分矩阵Y:")
print(vnk)
特征向量 V:[[ 0.707 -0.707][ 0.707 0.707]]
样本主成分矩阵 Y:[[-2.028 -0.82 -0.433 -0. 0.82 2.461][-0.296 0.046 0.433 0. -0.046 -0.137]]
正交矩阵V:
[[ 0.707 0.707][ 0.707 -0.707]]
样本主成分矩阵Y:
[[-2.028 -0.82 -0.433 0. 0.82 2.461][ 0.296 -0.046 -0.433 0. 0.046 0.137]]
16.2、16.3
见该链接
使用书籍:李航《机器学习方法》
习题解答:https://datawhalechina.github.io/statistical-learning-method-solutions-manual/#/
相关文章:

第16章 主成分分析:四个案例及课后习题
1.假设 x x x为 m m m 维随机变量,其均值为 μ \mu μ,协方差矩阵为 Σ \Sigma Σ。 考虑由 m m m维随机变量 x x x到 m m m维随机变量 y y y的线性变换 y i α i T x ∑ k 1 m α k i x k , i 1 , 2 , ⋯ , m y _ { i } \alpha _ { i } ^ { T } …...

股票分析系统设计方案大纲与细节
股票分析系统设计方案大纲与细节 一、引言 随着互联网和金融行业的迅猛发展,股票市场已成为重要的投资渠道。投资者在追求财富增值的过程中,对股票市场的分析和预测需求日益增加。因此,设计并实现一套高效、精准的股票分析系统显得尤为重要。本设计方案旨在提出一个基于大…...

.gitmodules文件
.gitmodules文件在Git仓库中的作用 .gitmodules 文件是 Git 版本控制系统中用来跟踪和管理子模块的配置文件。子模块允许你将一个 Git 仓库嵌套在另一个仓库中,这样可以方便地管理多个项目之间的依赖关系。 在 .gitmodules 文件中,通常会记录每个子模块…...

STM32 SPI世界:W25Q64 Flash存储器的硬件与软件集成策略
摘要 在嵌入式系统设计中,选择合适的存储解决方案对于确保数据的安全性和系统的可靠性至关重要。W25Q64 Flash存储器因其高性能和大容量成为STM32微控制器项目中的热门选择。本文将深入探讨STM32与W25Q64 Flash存储器的硬件连接、软件集成以及SPI通信的最佳实践。 …...
【计算机网络仿真】b站湖科大教书匠思科Packet Tracer——实验17 开放最短路径优先OSPF
一、实验目的 1.验证OSPF协议的作用; 二、实验要求 1.使用Cisco Packet Tracer仿真平台; 2.观看B站湖科大教书匠仿真实验视频,完成对应实验。 三、实验内容 1.构建网络拓扑; 2.验证OSPF协议的作用。 四、实验步骤 1.构建网…...

ChatGPT对话:python程序模拟操作网页弹出对话框
【编者按】单击一网页中的按钮,弹出对话框网页,再单击其中的“Yes”按钮,对话框关闭,请求并获取新网页。 可能ChatGPT第一次没有正确理解描述问题的含义,再次说明后,程序编写就正确了。 1问:pyt…...

利用亚马逊云科技云原生Serverless代码托管服务开发OpenAI ChatGPT-4o应用
今天小李哥继续介绍国际上主流云计算平台亚马逊云科技AWS上的热门生成式AI应用开发架构。上次小李哥分享了利用谷歌云serverless代码托管服务Cloud Functions构建Gemini Pro API,这次我将介绍如何利用亚马逊的云原生服务Lambda调用OpenAI的最新模型ChatGPT 4o。…...

Selenium 切换 frame/iframe
环境: Python 3.8 selenium3.141.0 urllib31.26.19说明: driver.switch_to.frame() # 将当前定位的主体切换为frame/iframe表单的内嵌页面中 driver.switch_to.default_content() # 跳回最外层的页面# 判断元素是否在 frame/ifame 中 # 126 邮箱为例 # …...
)
VOI(Virtual Operating System Infrastructure,虚拟操作系统基础架构)
VOI(Virtual Operating System Infrastructure,虚拟操作系统基础架构)架构在桌面虚拟化领域具有其独特的优势,使得它在某些场景下表现尤为出色。以下是几个具体场景: 1. 重载性能需求场景 表现: 高效利用…...
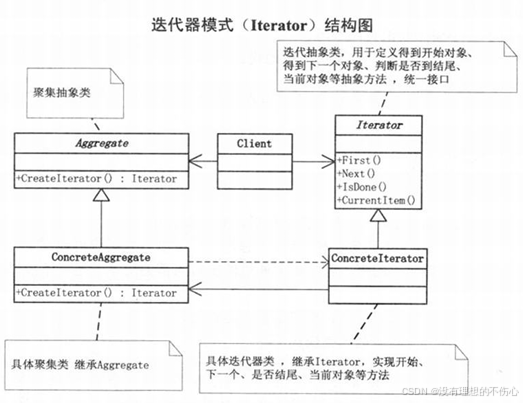
迭代器模式(大话设计模式)C/C++版本
迭代器模式 C #include <iostream> #include <string> #include <vector>using namespace std;// 迭代抽象类,用于定义得到开始对象、得到下一个对象、判断是否到结尾、当前对象等抽象方法,统一接口 class Iterator { public:Iterator(){};virtu…...

vue学习day04-计算属性、computed计算属性与methods方法、计算属性完整写法
10、计算属性 (1)概念: 基于现有的数据,计算出来的新属性。依赖于数据变化,自动重新计算。 (计算属性->可以将一段求值的代码进行封装) (2)语法: 1&a…...

关于力扣150题目——逆波兰表达式求值Java实现的三种解法
题目介绍 逆波兰表达式是一种后缀表达式,其运算符位于操作数之后。力扣150题目要求我们实现一个函数,计算给定逆波兰表达式的值。本文将介绍三种不同的Java实现方法来解决这个问题。 解法一:使用栈 这是最直观和常见的解法,使用…...

FTP与TFTP
1、TFTP(简单文件传输协议) TFTP是TCP/IP协议族中一个用来在客户机与服务器之间进行简单文件传输的协议,提供不复杂、开销不大的文件传输服务。 基于UDP协议 端口号:69 特点:简单、轻量级、易于实现 传输过程&…...

【Linux】System V信号量详解以及semget()、semctl()和semop()函数讲解
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...

JAVA预编译简单理解
目录 一、JSP预编译 二、JDBC预编译 一、JSP预编译 JSP(JavaServer Pages)是一种动态网页技术标准,它允许将Java代码嵌入到HTML页面中。当第一次请求一个JSP页面时,Web服务器(如Tomcat)会将JSP页面转换成一…...

nvm 管理多版本 node
1、下载 先不安装node 下载 nvm 1.1.10-setup.zip 解压:nvm:https://nvm.uihtm.com/ 新建nodejs/node、nodejs/nvm文件夹用于存放node版本和nvm安装路径 安装nvm:上述链接有安装教程 查看是否安装成功:重新打开cmd 输入 nvm nv…...

C++中的多重继承和虚继承:横向继承、纵向继承和联合继承;虚继承
多重继承 A.横向多重继承: B.纵向多重继承: C.联合多重继承: 因为 single 和 waiter 都继承了一个 worker 组件,因此 SingingWaiter 将包含两个 worker 组件,那么将派生类对象的地址赋给基类指针将出现二义性 那么如何…...

利用node连接mongodb实现一个小型后端服务系统demo
http 请求 实现get请求数据库数据;实现添加数据实现编辑数据实现删除数据实现导出txt文件、Excel文件实现查询数据库数据并利用导出为excel文件 node 版本 16.16.0 node 版本 18.16.0 会连接 MongoDB 数据库错误。 Connected to MongoDB failed MongoServerSele…...
)
大数据面试题之数据库(3)
数据库有必要建索引吗? MySQL缺点? 什么是脏读?怎么解决? 为什么要有三大范式,建数据库时一定要遵循吗? 数据库一般对哪些列建立索引?索引的数据结构? MySOL中索引的建立需要考虑哪些问题 关系型数据库与非关系型数据库区别 MySQL与Redis区别 …...

升级之道:精通Conda的自我升级艺术
升级之道:精通Conda的自我升级艺术 引言 Conda是Python和其他科学计算语言的强大包管理器,它不仅管理着包的安装和依赖,还负责自身的更新。随着开源社区的不断发展,Conda定期发布新版本以修复已知问题、增加新功能和提高性能。本…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...
