算法·高精度
高精度算法
- 分为四则运算加减乘除
适用条件
- 都高精度了,肯定时long long都会爆的情况——一般与阶乘有关
注意事项
- 用数组模拟位运算,最后在一起考虑进位
- 注意
res[i+1]+=res[i]/10;是"+="不是=
- 注意
- 两数相加,相乘数组的新长度会变,要正确计算!
- 加法:
len=max(lena,lenb)+1 - 乘法:
len=lena+lenb+1
- 加法:
- 位运算的公式
- 加法:
a[i] += b[i]; - 乘法:
res[i+j-1]+=a[i]*b[j];模拟乘法运算,一个数字乘以行的情况
- 加法:
- 对于阶乘:
- 最好是定义一个类bigInt,便于组织代码
for(int i=2;i<=n;i++){ x*i }利用循环模拟,不建议递归
加法模板
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
string stra, strb;
int a[5009];
int b[5009];
void solve() {cin >> stra >> strb;int lena = stra.size(), lenb = strb.size();for (int i = lena-1; i >= 0; i--) {a[lena - i] = stra[i]-'0';}/*for (int i = lena; i >= 1; i--) {cout << a[i];}cout << endl;*/for (int i = lenb - 1; i >= 0; i--) {b[lenb - i] = strb[i]-'0';}/*for (int i = lenb; i >= 1; i--) {cout << b[i];}cout << endl;*/int len = max(lena, lenb) + 2;for (int i = 1; i <= len; i++) {a[i] += b[i];}//for (int i = len; i >= 1; i--) {// cout << a[i] << " ";//}//cout << endl;for (int i = 1; i <= len; i++) {a[i + 1] += a[i] / 10;a[i] %= 10;}/*for (int i = len; i >= 1; i--) {cout << a[i] << " ";}*/for (; a[len]==0&&len>0;len--);if (len <=1) {cout << 0;return;}for (int i = len; i >= 1; i--) {cout << a[i];}
}
乘法模板
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
string stra, strb;
int a[5009];
int b[5009];
int res[5009];
void solve() {cin >> stra >> strb;int lena = stra.size(), lenb = strb.size();for (int i = lena-1; i >= 0; i--) {a[lena - i] = stra[i]-'0';}for (int i = lenb - 1; i >= 0; i--) {b[lenb - i] = strb[i]-'0';}int len = lena + lenb + 2;for (int i = 1; i <= lena; i++) {for (int j = 1; j <= lenb; j++) {res[i + j - 1] += a[i] * b[j];}}/*for (int i = 1; i <= 10; i++) {cout << res[i] << " ";}cout << endl;*/for (int i = 1; i <= len; i++) {res[i + 1] += res[i] / 10;res[i] %= 10;}/*for (int i = 1; i <= 10; i++) {cout << res[i] << " ";}*//*for (int i = len; i >= 1; i--) {cout << a[i] << " ";}*/for (; res[len]==0&&len>0;len--);if (len <1) {cout << 0;return;}for (int i = len; i >= 1; i--) {cout << res[i];}
}
阶乘模板
using namespace std;
using ll = long long;
int t,n,a,ct;
class bigInt {
public://构造一个类,避免重复开辟新空间int a[5009];int len;bigInt() {memset(a, 0, sizeof(a));a[1] = 1;len = 1;}void operator*(int b) {for (int i = 1; i <= len; i++) {a[i] *= b;}len += b/10+1;//扩容不是固定的+2!!!for (int i = 1; i <= len; i++) {a[i + 1] += a[i] / 10;a[i] %= 10;}for (; a[len]==0; len--);}void print() {for (int i = len; i >= 1; i--) {cout << a[i];}}
};
bigInt number;
void solve() {cin >> t;while (t--) {cin >> n >> a;if (n == 0) {//特判0!=1(也可以不特判)cout << (a == 1 ? 1 : 0); continue;}for (int i = 2; i <= n; i++) {number* i;//原地对number不断发生阶乘运算//你也可以定义=运算符,但是我懒}number.print();cout << endl;}
}
以下均为例题
阶乘数码
题目描述
求 n ! n! n! 中某个数码出现的次数。
输入格式
第一行为 t ( t ≤ 10 ) t(t \leq 10) t(t≤10),表示数据组数。接下来 t t t 行,每行一个正整数 n ( n ≤ 1000 ) n(n \leq 1000) n(n≤1000) 和数码 a a a。
输出格式
对于每组数据,输出一个整数,表示 n ! n! n! 中 a a a 出现的次数。
样例 #1
样例输入 #1
2
5 2
7 0
样例输出 #1
1
2
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
int t,n,a,ct;
class bigInt {
public:int a[5009];int len;bigInt() {memset(a, 0, sizeof(a));a[1] = 1;len = 1;}void operator*(int b) {for (int i = 1; i <= len; i++) {a[i] *= b;}len += b/10+1;//扩容不是固定的+2!!!for (int i = 1; i <= len; i++) {a[i + 1] += a[i] / 10;a[i] %= 10;}for (; a[len]==0; len--);}void print() {for (int i = len; i >= 1; i--) {cout << a[i];}}
};
bigInt number;
void solve() {cin >> t;while (t--) {cin >> n >> a;if (n == 0) {cout << (a == 1 ? 1 : 0); continue;}memset(number.a, 0, sizeof(number.a));number.a[1] = 1;number.len = 1;ct = 0;//初始化for (int i = 2; i <= n; i++) {number* i;//不断发生变换}/*number.print();cout << endl;*/for (int i = 1; i <= number.len; i++) {if (number.a[i] == a) {ct++;}}cout << ct<<endl;}
}
signed main() {std::ios::sync_with_stdio(false);std::cin.tie(0); std::cout.tie(0);solve();return 0;
}
相关文章:

算法·高精度
高精度算法 分为四则运算加减乘除 适用条件 都高精度了,肯定时long long都会爆的情况——一般与阶乘有关 注意事项 用数组模拟位运算,最后在一起考虑进位 注意res[i1]res[i]/10; 是""不是 两数相加,相乘数组的新长度会变&…...

Docker搭建kafka+zookeeper以及Springboot集成kafka快速入门
参考文章 【Docker安装部署KafkaZookeeper详细教程】_linux arm docker安装kafka-CSDN博客 Docker搭建kafkazookeeper 打开我们的docker的镜像源配置 vim /etc/docker/daemon.json 配置 { "registry-mirrors": ["https://widlhm9p.mirror.aliyuncs.com"…...

【cocos2dx】【iOS工程】如何保存用户在游戏内的绘画数据,并将数据以图像形式展示在预览界面
【cocos2dx】【iOS工程】如何保存用户在应用内的操作数据,并将数据以图像形式展示在预览界面 设备/引擎:Mac(11.6)/Mac Mini 开发工具:Xcode(15.0.1) 开发需求:如何保存用户在应用…...

拥抱应用创新,拒绝无谓的模型竞争
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

【源码+文档+调试讲解】旅游资源网站
摘 要 本论文主要论述了如何使用JAVA语言开发一个旅游资源网站 ,本系统将严格按照软件开发流程进行各个阶段的工作,采用B/S架构,面向对象编程思想进行项目开发。在引言中,作者将论述旅游资源网站的当前背景以及系统开发的目的&…...

Monaco 多行提示的实现方式
AI 代码助手最近太火爆,国内有模型厂商都有代码助手,代码助手是个比较典型的 AI 应用,主要看前端,后端的模型都差不多,国内外都有专门的代码模型。现在都是集中在 VSCode 和 Idea的插件,本文通过 Monaco 实…...

SpringMVC的架构有什么优势?——表单和数据校验(四)
#SpringMVC的架构有什么优势?——表单和数据校验(四) 前言 关键字: 机器学习 人工智能 AI chatGPT 学习 实现 使用 搭建 深度 python 事件 远程 docker mysql安全 技术 部署 技术 自动化 代码 文章目录 - - - - - 表单数据…...

Linux实战记录
踩坑实录: day2: 最坑:安装UB居然不知道创建文件夹。 1.虚拟机上不了网:多重置几次 网卡 2.Winscp链接主机: 用户名 就是 linux terminal中的 第一个用户名!...

时间、查找、打包、行过滤与指令的运行——linux指令学习(二)
前言:本节内容标题虽然为指令,但是并不只是讲指令, 更多的是和指令相关的一些原理性的东西。 如果友友只想要查一查某个指令的用法, 很抱歉, 本节不是那种带有字典性质的文章。但是如果友友是想要来学习的,…...

android CameraX构建相机拍照
Android CameraX 是一个 Jetpack 支持库,旨在简化相机应用的开发工作。它提供了一致且易用的API接口,适用于大多数Android设备,并可向后兼容至Android 5.0(API级别21)。 CameraX解决了在多种设备上实现相机功能时所遇…...

【普中】基于51单片机的矩阵电子密码锁LCD1602液晶显示 proteus仿真+程序+设计报告+讲解视频
【普中】基于51单片机的矩阵电子密码锁LCD1602液晶显示设计 1.主要功能:讲解视频:2.仿真3. 程序代码4. 设计报告5. 设计资料内容清单&&下载链接资料下载链接: 【普中】基于51单片机的矩阵电子密码锁LCD1602液晶显示设计 ( proteus仿真…...

工厂水电燃气表流量计等能耗计量仪表非侵入式拍照抄表的方案
在企业园区、工厂等企事业单位,传统的手动抄表方式已逐渐不能满足现代化、信息化管理的需求。为了提高抄表工作的效率,减少人工操作的误差,同时保障数据的安全性和实时性,我们提出了拍照采集抄表方案。本方案旨在通过拍照的方式&a…...

LLM大模型应用中的安全对齐的简单理解
LLM大模型应用中的安全对齐的简单理解 随着人工智能技术的不断发展,大规模语言模型(如GPT-4)的应用越来越广泛。为了保证这些大模型在实际应用中的性能和安全性,安全对齐(Safe Alignment)成为一个重要的概…...

clickhouse-jdbc-bridge rce
clickhouse-jdbc-bridge 是什么 JDBC bridge for ClickHouse. It acts as a stateless proxy passing queries from ClickHouse to external datasources. With this extension, you can run distributed query on ClickHouse across multiple datasources in real time, whic…...

java中Comparator函数的用法实例?
在Java中,Comparator接口用于比较两个对象的顺序,常用于集合的排序。自Java 8开始,Comparator接口得到了增强,提供了许多默认方法,使得排序逻辑更加灵活和强大。下面将通过几个实例来展示Comparator的用法。 示例1&am…...

mysql实战入门-基础篇
目录 1、MySQL概述 1.1、数据库相关概念 1.2、MySQL数据库 1.2.1、版本 1.2.2、下载 1.2.3、安装 输入MySQL中root用户的密码,一定记得记住该密码 1.2.4、启动停止 1.2.5、客户端连接 1.2.6、数据模型 2、SQL 2.1、SQL通用语法 2.2、SQL分类 2.3、DDL 2.3.1、数据…...
阶段三:项目开发---民航功能模块实现:任务24:航空实时监控
任务描述 内 容:地图展示、飞机飞行轨迹、扇区控制。航空实时监控,是飞机每秒发送坐标,经过终端转换实时发送给塔台,为了飞机位置的精准度,传输位置的密度很大,在地图位置显示不明显。本次为了案例展示效…...

手机容器化 安装docker
旧手机-基于Termux容器化 1、安装app 在手机上安装Termux或ZeroTermux(Termux扩展) 1.1 切换源 注:可以将termux进行换源,最好采用国内源,例如:清华源等 更新包列表和升级包(可选࿰…...
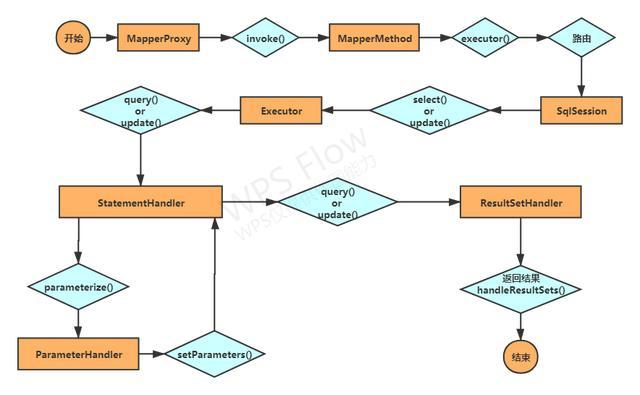
科普文:深入理解Mybatis
概叙 (1) JDBC JDBC(Java Data Base Connection,java数据库连接)是一种用于执行SQL语句的Java API,可以为多种关系数据库提供统一访问,它由一组用Java语言编写的类和接口组成.JDBC提供了一种基准,据此可以构建更高级的工具和接口,使数据库开发人员能够编写数据库应用程序。 优点…...

称重传感器有哪些种类
有关称重传感器的知识,称重传感器是众多传感器产品中的一种,也是很常用的传感器之一,那么称重传感器有哪些种类,称重传感器的分类方式是什么样的,一起来了解下。 称重传感器的分类 主要有六种称重传感器类型…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...
