【密码学】从有限状态自动机到密钥流生成器
本文是对流密码内容的拓展,在流密码中种子密钥通过一个伪随机数生成器产生一个与明文等长的伪随机密钥流。而本文的内容就是在回答这样两个问题:
- 伪随机密钥流是如何生成的?
- 流密码、流密钥生成器和有限状态自动机之间是什么关系?
一、什么是有限状态自动机?
(1)定义
有限状态自动机(Finite State Machine,FSM)是具有离散输入和输出(输入集合与输出集合均有限)的一种数学模型。用于描述和分析系统的行为,特别是那些可以根据输入信号在不同状态之间切换的系统。由以下三个部分组成:
① 有限状态集
状态集:一组有限的状态,表示系统可能处于的条件或模式。每个状态代表系统的一个特定配置。
② 有限输入字符集和有限输出字符集
输入集:一组有限的输入符号,这些符号可以触发状态的转换。
输出集:一组可能的输出符号,这些符号由自动机根据当前状态和输入产生。
③ 转移函数
状态转移函数:定义了在给定当前状态和输入的情况下,自动机会转移到哪个新状态。这个函数是自动机行为的核心。
输出函数:在某些FSM模型中,还定义了一个输出函数,它根据当前状态(和可能的输入)决定自动机的输出。
公式代表的含义是在状态为,输入为
时,输出为
,而状态转移为
(2)表现形式一:转移图
有限状态自动机(FSM)经常用有向图来表示,这种图形化的表示方法被称为转移图或状态图。转移图提供了一种直观的方式来展示FSM的结构和行为,便于理解和分析。

-
节点:转移图中的每个节点代表FSM中的一个状态。通常,节点会被标记以表示其状态名称或编号。
-
有向边:边表示从一个状态到另一个状态的转移。每条有向边都关联有一个或多个输入符号,这些输入符号触发从源状态到目标状态的转移。边上的标签通常包含触发转移的输入符号。
-
初始状态:转移图中通常会明确标出一个初始状态,表示FSM启动时的默认状态。初始状态通常用一个箭头指向或特殊形状的节点来表示。
-
终止状态:在某些FSM中,特定的状态被标记为终止状态或接受状态,表示自动机完成了一个特定任务或识别了一个特定输入序列。这些状态通常用双圆圈或类似标记来表示。
-
循环:转移图中可能存在从一个状态回到自身的边,这表示在特定输入下状态不会改变,形成一个循环。
-
分支:对于非确定性有限状态自动机(NFA),一个状态可能有多条边指向同一个或不同的状态,表示对于同一输入可能有多种响应。
(2)表现形式二:矩阵
除了使用转移图直观地表示有限状态自动机(FSM)的状态和转移外,我们还可以使用矩阵来数学化地描述FSM的行为。

有限状态自动机的矩阵表示主要有两种类型的矩阵:
-
状态转移矩阵:这是最常见的一种矩阵表示法,它描述了当前状态和输入组合下的下一个状态。如果FSM有n个状态,并且输入符号集合大小为m,则状态转移矩阵将是一个n×(m×n)的矩阵。每一行对应于一个当前状态,每一列对应于一个特定的输入,而矩阵中的元素则表示该输入下从当前状态转移到的下一个状态。如果FSM是非确定性的,那么矩阵中的元素可以是一个状态集,表示从当前状态出发,给定输入后可能达到的多个状态。
-
输出矩阵(对于带有输出的FSM):在带有输出功能的FSM中,每个状态转移不仅涉及状态的变化,还可能伴随有输出。输出矩阵描述了在给定状态和输入的情况下,FSM产生的输出。如果FSM有n个状态,m个输入符号,k个可能的输出,则输出矩阵将是n×(m×k)的矩阵,其中矩阵中的每个元素表示在特定状态和输入下产生的输出。
二、密钥流生成器
(1)有限状态自动机怎么转换成密钥流生成器?
将有限状态自动机(FSM)转换成密钥流生成器通常是在设计密码系统时的一个步骤,尤其是对称加密中流密码的设计。流密码使用密钥流与明文进行逐位异或操作,以产生密文。密钥流生成器可以认为就是一个参数为的有限状态自动机。如下图:
由一个输出符号集、一个状态集
、两个函数
和
以及一个初始状态
组成。

状态转移函数:将当前状态
变为一个新状态
输出函数:将当前状态
变为输出符号集中的一个元素
(2)密钥流生成器设计的关键
密钥流的生成需要满足两个关键要求:随机性和不可预测性,确保攻击者无法轻易推断出密钥流的后续部分。
密钥流生成器设计的关键在于找出适当的状态转移函数和输出函数。使得输出序列满足密钥流序列应该满足的随机性条件,并且要求在设备上是节省的和容易实现的。
一般采样线性的状态转移函数和非线性的输出函数,这样能够进行深入的分析并可以得到好的生成器。所以密钥流生成器可以分成两个部分:驱动部分(包含线性组件)和非线性组合部分

- 驱动部分:负责控制生成器的状态转移过程。这通常涉及到一种或多种线性反馈移位寄存器(LFSRs),它们通过线性反馈规则更新状态。驱动部分的主要目标是生成一系列统计特性良好的伪随机比特序列,这些序列随后会被馈送到非线性组合部分。

- 非线性组合部分:任务是接收来自驱动部分的序列,并通过非线性变换将其转化为最终的密钥流输出。增加了输出序列的不可预测性,提高了生成器的整体安全性。

三、总结
流密码作为密码学领域中的一个重要分支,它采用了一种动态的、逐位加密的技术,通过将明文与一个同长度的密钥流进行异或运算,实现了数据的安全传输和存储。这里的“逐位”加密,意味着每一个明文字符或比特位都会与相应的密钥流位进行一对一的加密操作。
然而,直接使用与明文相同长度的密钥流在实际应用中面临着严峻的挑战,尤其是密钥分发和存储方面的问题。为了解决这一难题,密码学家们设计出了密钥流生成器——一种能够从一个较短的种子密钥出发,生成足够长、看似随机的密钥流的算法。这种生成的密钥流,虽然源自于简短的种子,但经过精心设计后,其长度可轻松匹配任何规模的明文,从而解决了密钥长度受限的问题。
密钥流生成器的设计灵感来源于有限状态自动机,这是一种数学模型,用于描述系统如何基于当前状态和输入信号,在一组预定义状态之间进行转换的过程。在流密码的背景下,有限状态自动机被巧妙地运用,通过一系列复杂的内部状态变化,将种子密钥作为初始状态,逐步演进生成所需的密钥流。这一过程不仅保证了密钥流的不可预测性和随机性,同时也确保了生成器的高效性和实用性。
相关文章:

【密码学】从有限状态自动机到密钥流生成器
本文是对流密码内容的拓展,在流密码中种子密钥通过一个伪随机数生成器产生一个与明文等长的伪随机密钥流。而本文的内容就是在回答这样两个问题: 伪随机密钥流是如何生成的?流密码、流密钥生成器和有限状态自动机之间是什么关系?…...

3.相机标定原理及代码实现(opencv)
1.相机标定原理 相机参数的确定过程就叫做相机标定。 1.1 四大坐标系及关系 (1)像素坐标系(单位:像素(pixel)) 像素坐标系是指相机拍到的图片的坐标系,以图片的左上角为坐标原点&a…...

Centos7 安装Docker步骤及报错信息(不敢说最全,但是很全)
一、操作系统要求: 要安装Docker Engine,您需要CentOS 7及以上的维护版本。存档版本不受支持或测试。必须启用centos临时存储库。默认情况下,此存储库已启用,但如果已禁用,则需要重新启用它。建议使用overlay2存储驱动…...

【C语言】符号优先级详解
C语言符号优先级详细解析 在C语言中,不同的运算符具有不同的优先级和结合性,这决定了在表达式中运算符的计算顺序。理解这些优先级和结合性是正确编写和理解C语言程序的基础。本文将详细解析C语言中的符号优先级,包括各类运算符的优先级、结…...

天翼云高级运维工程师202407回忆题库 最新出炉
备考天翼云高级运维工程师 必须备考天翼云 之前觉得外企牛批 然后民企,拔地而起,民企也不错,工资高,有钱途 现在看来看去,还是国企好,体制内的,有保障,树大根深 有必要备考下天…...

在Python中什么是上下文管理器以及如何使用with语句来管理资源
什么是上下文管理器? 在Python中,上下文管理器(Context Manager)是一种支持with语句的协议,允许对象管理资源,如文件、线程锁的获取和释放、数据库连接等。上下文管理器负责资源的分配和释放,确…...

(四)、python程序--贪吃蛇游戏
一、绪论 贪吃蛇游戏。 已实现功能: 1、上下左右移动; 2、吃食物,随机生成食物; 3、碰撞检测,判断是否游戏结束。 二、代码分享 1、main.py import pygame import sys import food as c_food import snake as c…...

什么是DNS欺骗
DNS欺骗(DNS Spoofing),也称为DNS缓存中毒(DNS Cache Poisoning),是一种网络攻击形式,攻击者通过操纵DNS记录,将用户重定向到一个伪造的、恶意的网站。这些恶意网站可能看起来与用户…...

C++实现对结构体信息排序
思路解读: 定义结构体 Student: 结构体 Student 用来表示学生信息,包含两个成员变量:name(学生姓名)和 score(学生分数)。Student 结构体定义了一个构造函数,用于初始化 name 和 sco…...

[CTF]-PWN:House of Cat堆题型综合解析
原理: 调用顺序: exit->_IO_wfile_jumps->_IO_wfile_seekoff->_IO_switch_to_wget_mode _IO_wfile_seekoff源码: off64_t _IO_wfile_seekoff (FILE *fp, off64_t offset, int dir, int mode) {off64_t result;off64_t delta, new…...
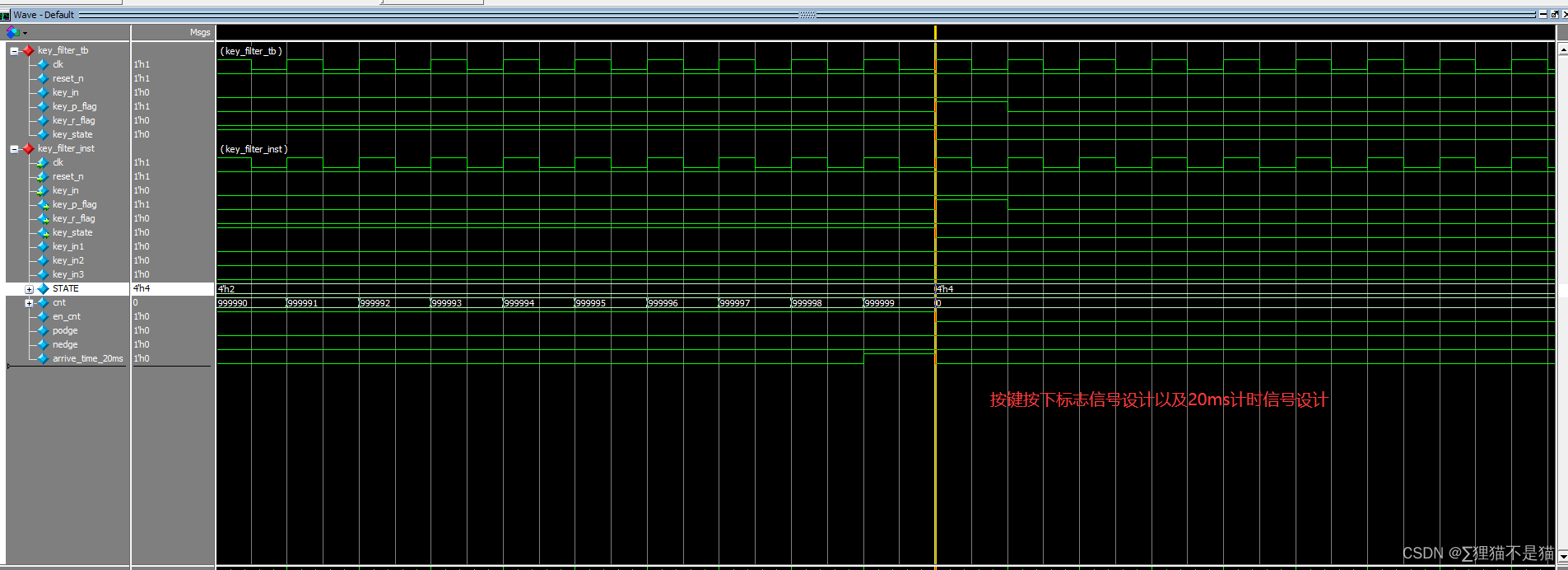
18.按键消抖模块设计(使用状态机,独热码编码)
(1)设计意义:按键消抖主要针对的时机械弹性开关,当机械触点断开、闭合时,由于机械触点的弹性作用,一个按键开关在闭合时不会马上稳定地接通,在断开时也不会一下子就断开。因而在闭合以及断开的瞬…...

【Hec-HMS】第一期:模型简介及软件安装
HEC-HMS模型简介及软件安装 HEC-HMS模型简介建模思路 HEC-HMS软件安装步骤1:安装InstallShield Wizard步骤2:安装HEC-HMS 参考 HEC-HMS模型简介 HEC-HMS(The Hydrologic Engineering Center’s-Hydrologic Modelimng System),美国陆军工程兵…...

逻辑回归不是回归吗?那为什么叫回归?
RNN 逻辑回归不是回归吗?那为什么叫回归?逻辑回归的基本原理逻辑函数(Sigmoid函数)二元分类 为什么叫做“回归”?逻辑回归的应用场景总结 逻辑回归不是回归吗?那为什么叫回归? 逻辑回归&#x…...

Activity对象的部分常见成员变量
在Android开发中,Activity 类是一个非常重要的类,它代表了应用程序中的一个屏幕。每个Activity都有一系列的成员变量和方法,这些成员变量通常用于控制和管理活动生命周期、UI界面元素、应用资源等。虽然具体的成员变量会根据Android的不同版本…...
)
量化交易策略:赌徒在股市会运用凯利公式(附python代码)
一、凯利公式的历史 凯利公式(Kelly Criterion)是由美国贝尔实验室物理学家约翰拉里凯利(John Larry Kelly)于1956年提出的,用于计算最优投资比例的一种数学公式。凯利公式的核心思想是:在期望收益和风险之间找到一个平衡点,使得投资者在承担一定风险的情况下,能够获得…...
)
信息系统项目管理师【一】英文选择题词汇大全(1)
一、计算机相关词汇 数据挖掘 Data Mining分布式计算 Distributed Computing云计算 Cloud Computing物联网 IOT Internet of Things大数据 Big Data人工智能 artificial intelligence互联网 Internet plus区块链 Blockchain5G 5th-Generation感知层 sensing layer机器学习 mac…...

怎么判断自己是否适合学习PMP?
判断自己是否适合学习PMP项目管理专业人士认证,可以从以下几个方面进行考量: 1、职业发展需求: 如果您在项目管理领域工作,或计划未来从事相关工作,PMP认证能显著提升您的竞争力。 对于项目经理、产品经理、技术领导…...

最新的数据防泄密方案来袭!
沙箱技术作为一种先进的数据安全解决方案,在数据防泄密领域发挥着日益重要的作用。它通过构建一个隔离的虚拟环境,使得应用程序在该环境中运行,从而隔离了应用程序对系统资源的直接访问,有效防止了数据泄露的风险。 一、沙箱技术在…...

Python数据处理之高效校验各种空值技巧详解
概要 在编程中,处理空值是一个常见且重要的任务。空值可能会导致程序异常,因此在进行数据处理时,必须确保数据的有效性。Python 提供了多种方法来处理不同数据对象的空值校验。本文将详细介绍如何对Python中的各种数据对象进行空值校验,并包含相应的示例代码,帮助全面掌握…...

Spring Boot与RSocket的集成
Spring Boot与RSocket的集成 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 一、引言 RSocket是一个基于异步、消息驱动的网络协议,旨在解决微服…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
