边缘概率密度、条件概率密度、边缘分布函数、联合分布函数关系
目录
- 二维随机变量及其分布
- 离散型随机变量
- 连续型随机变量
- 边缘分布
- 边缘概率密度
- 举例
- 边缘概率密度
- 条件概率密度
- 边缘概率密度与条件概率密度的区别
- 边缘概率密度
- 条件概率密度
- 举个具体例子
- 参考资料
二维随机变量及其分布
离散型随机变量

把所有的概率,都理解成不同质量的物体,这些物体就分布在二维平面上(左图)。再把这些物体都看成是精简的质点。
如果 f ( x , y ) f(x,y) f(x,y)是其中的某个点的话,那么 F ( x , y ) = P ( X ≤ x , Y ≤ y ) F(x,y)=P(X≤x, Y≤y) F(x,y)=P(X≤x,Y≤y)就是该点左下角所有质点的质量叠加。

连续型随机变量
它就不再是一个个质点了,而是一个个物体。 F ( x , y ) F(x,y) F(x,y)叫联合分布函数。其分布函数仍然是质量。概率密度就是面密度(例如kg/m^2).

如果你要给爱人送一个礼物,中间部分是黄金做的,边缘部分是铁做的。从金到铁有一个渐变的过程,这就导致每个点的密度不太一样。(此处,这个物体是个薄片、扁平的,不研究它的厚度)。这个密度就叫概率密度 f ( x , y ) f(x,y) f(x,y)

F ( x , y ) F(x,y) F(x,y)还是表示点 ( x , y ) (x,y) (x,y)左下角的质量。也就是对面密度做积分,得到的就是质量。

把质量对应概率,把密度对应成面密度。
边缘分布

F X ( x ) = P ( X ≤ x ) F_X(x)=P(X≤x) FX(x)=P(X≤x)与 F ( x , y ) = P ( X ≤ x , Y ≤ y ) F(x,y)=P(X≤x, Y≤y) F(x,y)=P(X≤x,Y≤y)的关系,如下图所示。

边缘概率密度

觉得礼品不太好看,沿着y方向压缩,一直压缩到从数学上来说y的厚度已经没有了(0),如下图所示

此时,这根线的密度,就叫线密度(g/cm)。

压缩过程如下。其代表的是x位于不同点的时候的密度。


所以,右侧图中线上每个点的质量(概率),其实就是左侧图片中对应的竖线的质量,竖直做积分。
同理 F Y ( y ) F_Y(y) FY(y)就是水平做积分。
举例
下图中,黄颜色代表大多数人都位于这个位置,集中在身高和体重的均值附近,概率密度比较大。

F(1.6, 100),计算的是身高≤1.6m,体重≤100kg的概率。从质量的角度来说,算的是质量。

而边缘概率,是身高小于1.6的人的概率,也可以理解为x<1.6的质量。

边缘概率密度
把同身高、不同体重的人进行积分,就得到单独身高的密度分布,

条件概率密度
它和边缘概率密度有点像,但又不一样。它研究的是单独某一条线(水平或竖直)的密度问题。常用于求条件概率密度。



如下图,让Y=b,此时就叫条件概率密度。只研究一条线的概率密度,


以身高体重为例子,研究体重为101斤的人,它的身高的分布,


同样,身高1m85的人,其体重的分布


边缘概率密度与条件概率密度的区别
让我用更简单的方式来解释这两个概念。
边缘概率密度
想象一下,你和朋友在玩一种抽奖游戏。这个抽奖游戏有两个转盘,一个转盘上有各种颜色(红色、绿色、蓝色),另一个转盘上有各种动物(狗、猫、鸟)。每次抽奖,你会同时转动这两个转盘,然后得到一个颜色和一个动物的组合。
现在,我们只对颜色感兴趣,不管动物是什么。这就像我们只看第一个转盘,不看第二个转盘。这时候,我们就得到了颜色的边缘概率密度。就是说,我们只关心颜色的分布情况,比如有多少次是红色的,有多少次是绿色的等等。
条件概率密度
继续这个抽奖游戏的例子。如果这次我们知道抽到的动物是狗,我们想知道在这种情况下颜色的分布情况。比如,在抽到狗的时候,有多少次是红色的,有多少次是绿色的等等。这就是条件概率密度。
条件概率密度告诉我们:在已知某个条件下(比如已经知道抽到的是狗),其他东西(比如颜色)的分布情况。
举个具体例子
假设我们玩了很多次这个游戏,统计结果如下:
- 总共抽了100次。
- 抽到红色的有30次,绿色的有50次,蓝色的有20次(这就是颜色的边缘概率)。
- 抽到狗的有40次,猫的有30次,鸟的有30次。
- 在抽到狗的40次里,红色的有10次,绿色的有20次,蓝色的有10次(这就是抽到狗时颜色的条件概率)。
所以,边缘概率密度就像我们只看颜色的总体情况,而条件概率密度就像我们知道抽到狗后再来看颜色的分布情况。
参考资料
[1] 边缘概率密度,条件概率密度,边缘分布函数,联合分布函数关系;
相关文章:

边缘概率密度、条件概率密度、边缘分布函数、联合分布函数关系
目录 二维随机变量及其分布离散型随机变量连续型随机变量边缘分布边缘概率密度举例边缘概率密度 条件概率密度边缘概率密度与条件概率密度的区别边缘概率密度条件概率密度举个具体例子 参考资料 二维随机变量及其分布 离散型随机变量 把所有的概率,都理解成不同质量…...

软件架构之系统分析与设计方法(2)
软件架构之系统分析与设计方法(2) 8.4 面向对象的分析与设计8.4.1 面向对象的基本概念8.4.2 面向对象分析8.4.3 统一建模语言 8.5 用户界面设计8.5.1 用户界面设计的原则8.5.2 用户界面设计过程 8.6 工作流设计8.6.1 工作流设计概述8.6.2 工作流管理系统 8.7 简单分…...

AD确定板子形状
方法1 修改栅格步进值,手动绘制 https://cnblogs.com/fqhy/p/13768031.html 方法2 器件摆放确定板子形状 https://blog.csdn.net/Mark_md/article/details/116445961...

CSS【详解】边框 border,边框-圆角 border-radius,边框-填充 border-image,轮廓 outline
边框 border border 是以下三种边框样式的简写: border-width 边框宽度 —— 数值 px(像素),thin(细),medium(中等),thick(粗)border-style 边框线型 —— none【默认值…...

Error: EBUSY: resource busy or locked, rmdir...npm install执行报错
Error: EBUSY: resource busy or locked, rmdir...npm install执行报错 你一个文件夹目录开了两个cmd命令行(或者powershell),关掉一个就好了。...

Hot100-排序
1.快排 215. 数组中的第K个最大元素 - 力扣(LeetCode) (1)第k大的元素在排序数组中的位置是nums.length - k。 假设我们有一个数组nums [3, 2, 1, 5, 6, 4],并且我们想找到第2大的元素。 步骤 1:排序数…...
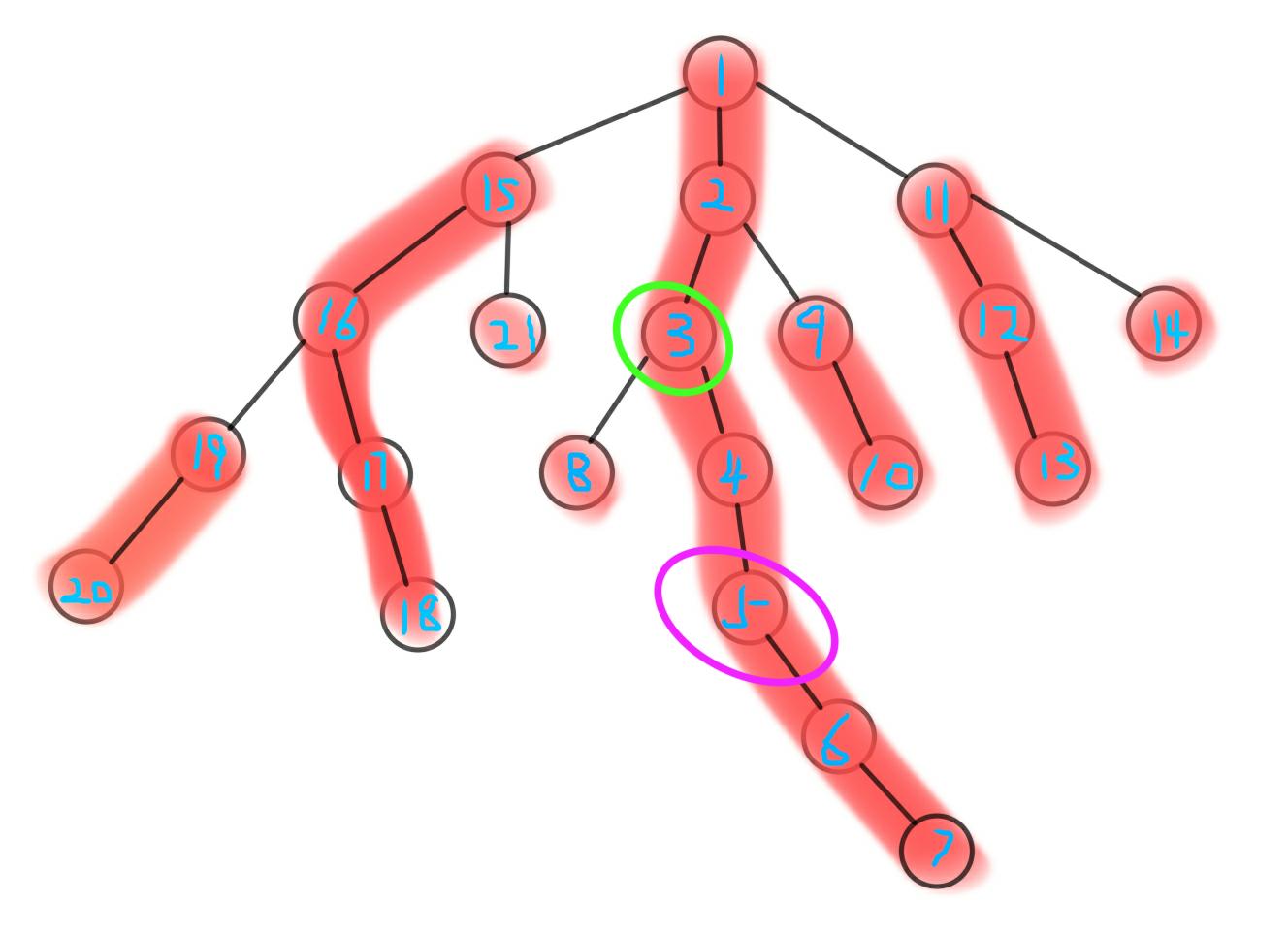
树链剖分相关
树链剖分这玩意儿还挺重要的,是解决静态树问题的一个很好的工具~ 这里主要介绍一下做题时经常遇到的两个操作: 1.在线求LCA int LCA(int x,int y){while(top[x]!top[y])if(dep[top[x]]>dep[top[y]]) xfa[top[x]];else yfa[top[y]];return dep[x]&l…...

如何将Grammarly内嵌到word中(超简单!)
1、下载 安装包下载链接见文章结尾 官网的grammarly好像只能作为单独软件使用,无法内嵌到word中🧐🧐🧐 2、双击安装包(安装之前把Office文件都关掉) 3、安装完成,在桌面新建个word文件并打开 注…...

OTG -- 用于FPGA的ULPI接口芯片USB3320讲解(续)
目录 1 背景 2 USB3320在FPGA上的应用 1 背景 最近使用FPGA驱动USB PHY实现高速USB功能,为了方便,购买了一块微雪的USB3300子板,发现怎么都枚举不了,使用逻辑分析仪抓取波形,和STM32F407USB3300波形进行对比…...

了解劳动准备差距:人力资源专业人员的战略
劳动准备差距是一个紧迫的问题,在全球人事部门回应,谈论未开发的潜力和错过的机会。想象一下,人才和需求之间的悬崖之间有一座桥,这促使雇主思考:我们是否为员工提供了足够的设备来应对未来的考验? 这种不…...

SAP PS学习笔记02 - 网络,活动,PS文本,PS文书(凭证),里程碑
上一章讲了PS 的概要,以及创建Project,创建WBS。 SAP PS学习笔记01 - PS概述,创建Project和WBS-CSDN博客 本章继续讲PS的后续内容。包括下面的概念和基本操作,以及一些Customize: - 网络(Network…...

Github 2024-07-07php开源项目日报 Top9
根据Github Trendings的统计,今日(2024-07-07统计)共有9个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量PHP项目9Blade项目2JavaScript项目1Laravel:表达力和优雅的 Web 应用程序框架 创建周期:4631 天开发语言:PHP, BladeStar数量:75969 个Fork数…...
第二十六天 | 452. 用最少数量的箭引爆气球、435. 无重叠区间、763. 划分字母区间)
算法训练(leetcode)第二十六天 | 452. 用最少数量的箭引爆气球、435. 无重叠区间、763. 划分字母区间
刷题记录 452. 用最少数量的箭引爆气球思路一思路二 435. 无重叠区间763. 划分字母区间 452. 用最少数量的箭引爆气球 leetcode题目地址 思路一 先按起始坐标从小到大排序。排序后找交集并将交集存入一个数组中,遍历气球数组从交集数组中找交集,找到与…...

Ubuntu 下 Docker安装 2024
Ubuntu 下 Docker安装 2024 安装1.卸载老版本2.更新apt包索引3.安装必要工具包4.添加Docker GPG秘钥5.配置仓库源6.安装Docker Engine7.启动docker 国内镜像源下架的解决办法1.修改文件 /etc/docker/daemon.json2.换源3.查看是否换源成功4.重启 安装 1.卸载老版本 sudo apt-ge…...
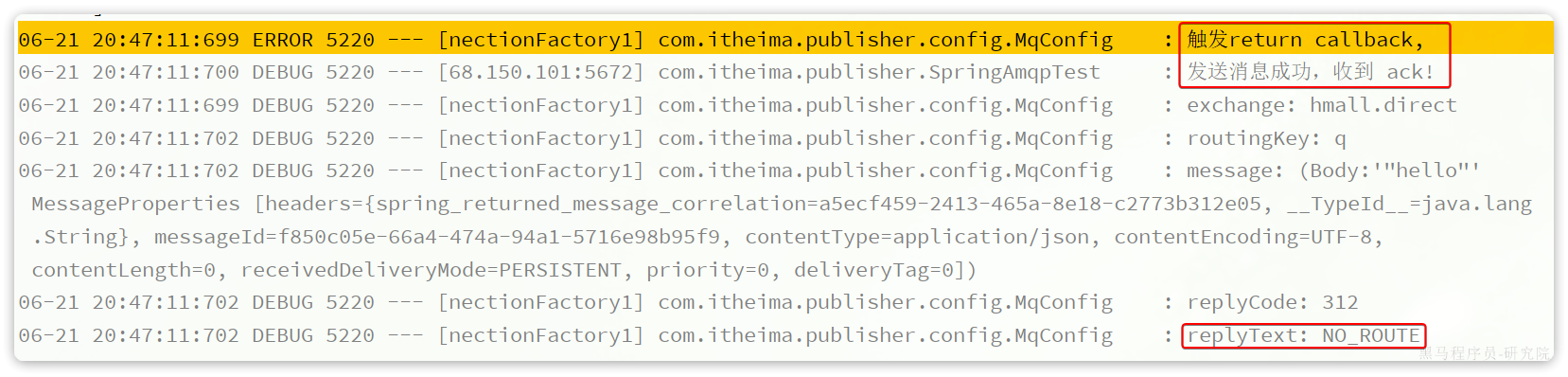
发送者的可靠性
这篇文章是了解MQ消息的可靠性,即:消息应该至少被消费者处理1次 那么问题来了: 我们该如何确保MQ消息的可靠性?如果真的发送失败,有没有其它的兜底方案? 首先,我们一起分析一下消息丢失的可能…...

Profibus_DP转ModbusTCP网关模块连马保与上位机通讯
Profibus转ModbusTCP网关模块(XD-ETHPB20)广泛应用于工业自动化领域。例如,可以将Profibus网络中的传感器数据转换为ModbusTCP协议,实现数据的实时监控和远程控制。本文介绍了如何利用Profibus转ModbusTCP网关(XD-ETHP…...

移动应用:商城购物类,是最常见的,想出彩或许就差灵犀一指
在移动应用中,商城购物类的非常常见,模式也非常成熟,想要设计的出彩也是有难度的,这次分享一些不同的。...

linux 查看历史命令列表来访问之前的内容的命令是:history
在Linux中,要查看历史命令列表以访问之前的内容,你可以使用history命令。这个命令会显示你当前shell会话(或者,如果你指定了参数,可能是所有会话)中执行过的命令列表。 基本用法 简单地输入history并按下…...

NAS免费用,鲁大师 AiNAS正式发布,「专业版」年卡仅需264元
7月10日,鲁大师召开新品发布会,正式发布旗下以“提供本地Ai部署和使用能力以及在线NAS功能”并行的复合软件产品:鲁大师 AiNAS。 全新的鲁大师 AiNAS将持续满足现如今大众对于数字化生活的全新需求,将“云存储”的便捷与NAS的大容…...

spring监听事件
1、spring-监听事件基本原理 Spring的事件监听机制和发布订阅机制是很相似的:发布了一个事件后,监听该类型事件的所有监听器会触发相应的处理逻辑 2、Spring 监听事件相关规范 在Spring中,事件监听机制主要涉及到了一下几个关键的规范&#x…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
