数据结构(3.8)——栈的应用

栈在括号匹配中的应用

流程图

代码

#include <stdio.h>
#include <stdlib.h>
#define MaxSize 10typedef struct {char data[MaxSize];int top;
} SqStack;// 初始化栈
void InitStack(SqStack* S) {S->top = -1; // 初始化栈顶指针
}// 判空
bool StackEmpty(SqStack* S) {if (S->top == -1) {return true;} else {return false;}
}// 入栈
bool Push(SqStack* S, char x) {if (S->top == MaxSize - 1) { // 栈满，报错return false;} else {S->top = S->top + 1; // 指针先加1S->data[S->top] = x; // 新元素入栈return true;}
}// 出栈
bool Pop(SqStack* S, char* x) {if (StackEmpty(S)) {return false;} else {*x = S->data[S->top]; // 栈顶元素先出栈S->top = S->top - 1; // 指针减1return true;}
}// 括号匹配检查
bool bracketCheck(char str[], int length) {SqStack S;InitStack(&S); // 初始化一个栈for (int i = 0; i < length; i++) {if (str[i] == '(' || str[i] == '[' || str[i] == '{') {Push(&S, str[i]); // 扫描到左括号，入栈} else {if (StackEmpty(&S)) { // 扫描到右括号，且当前栈空return false; // 匹配失败}char topElem;Pop(&S, &topElem); // 栈顶元素出栈if (str[i] == ')' && topElem != '(') {return false;}if (str[i] == ']' && topElem != '[') {return false;}if (str[i] == '}' && topElem != '{') {return false;}}}return StackEmpty(&S); // 检索全部括号后，栈空说明匹配成功
}int main() {char str[] = "{([()])}";int length = sizeof(str) / sizeof(str[0]) - 1; // 计算字符串长度，减1是为了去掉结尾的'\0'if (bracketCheck(str, length)) {printf("括号匹配成功\n");} else {printf("括号匹配失败\n");}return 0;
}

栈在表达式求值中的应用

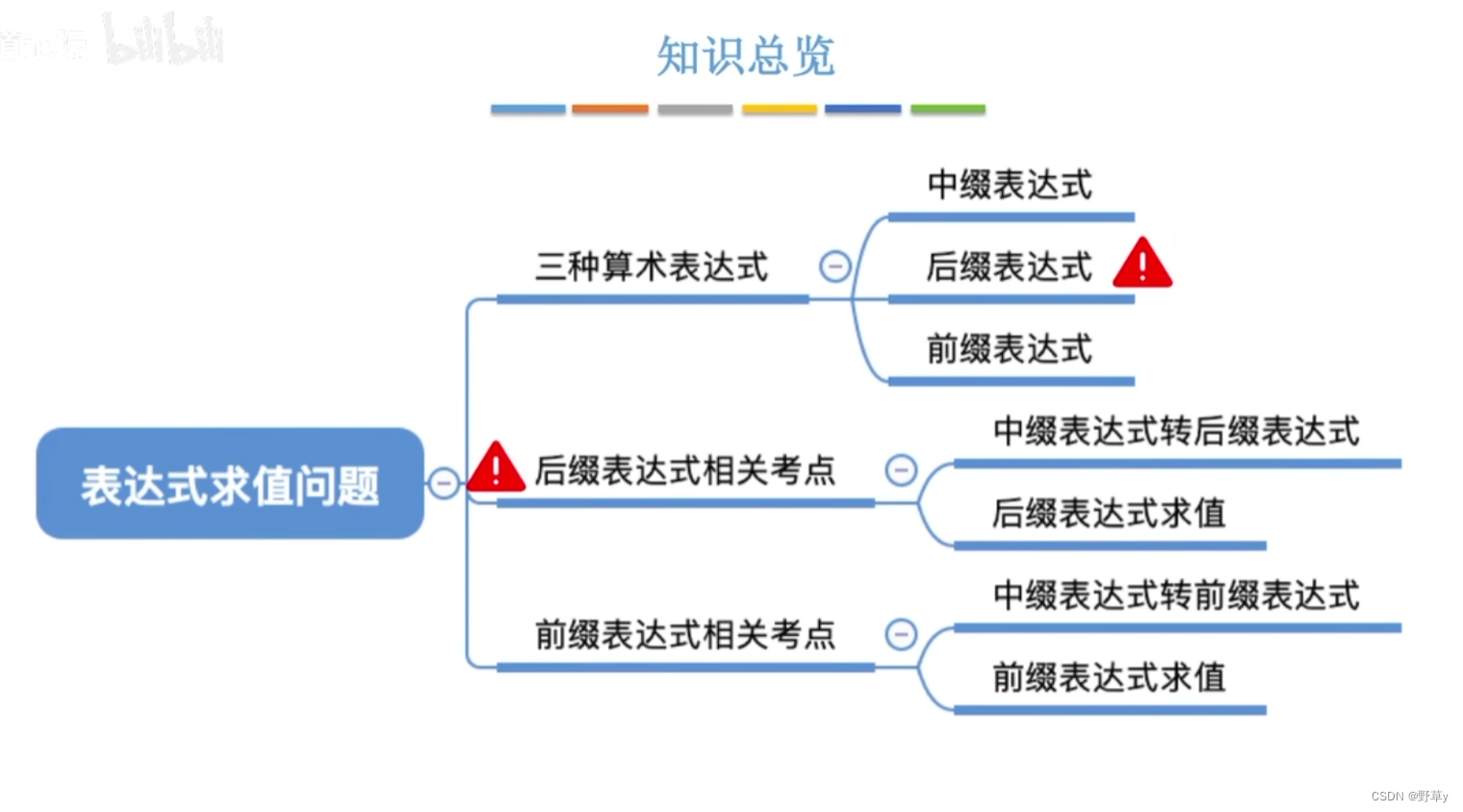
中缀、后缀、前缀表达式

中缀表达式

运算符在两个操作数中间：

1. a + b
2. a + b - c
3. a + b - c * d

后缀表达式

运算符在两个操作数后面：

1. ab +
2. ab + c-或者a bc - +
3. ab + cd * -

前缀表达式

运算符在两个操作数前面：

1. + ab
2. - + ab c
3. - + ab * cd

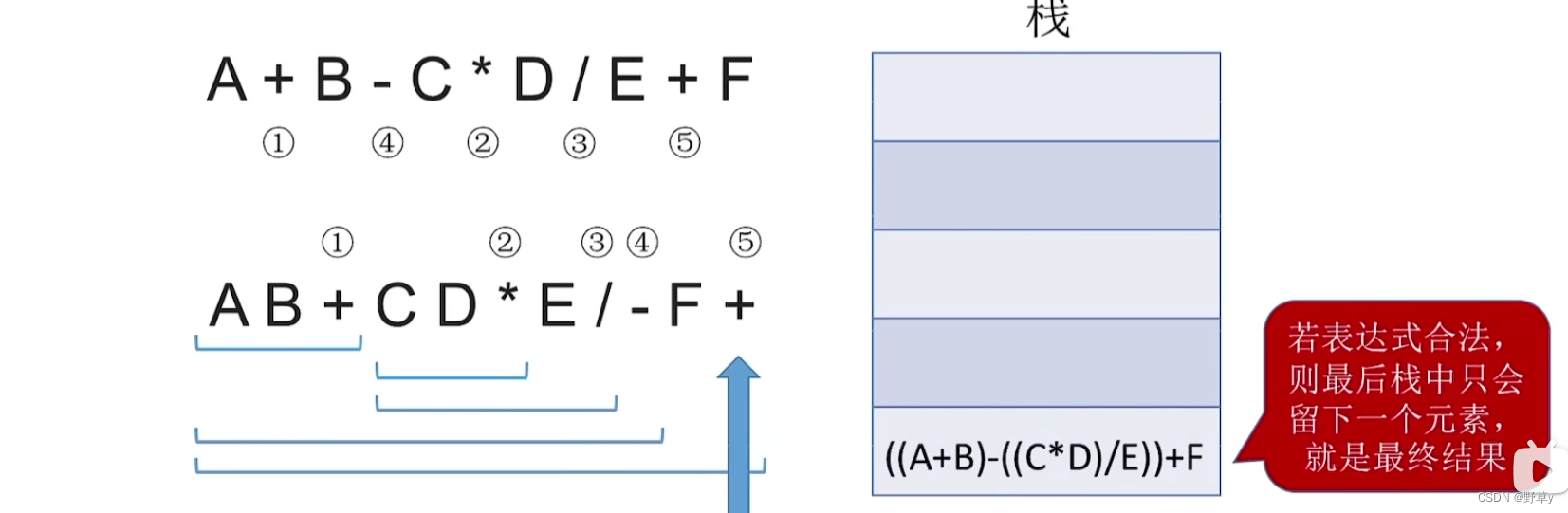
中缀表达式转后缀表达式(手算)

1. 确定中缀表达式中各个运算符的运算顺序
2. 选择下一个运算符，按照[左操作数 右操作数 运算符]的方式组合成一个新的操作数（若运算顺序不唯一，则后缀表达式也不唯一）
3. 如果还有运算符没被处理，就继续2步骤

例：

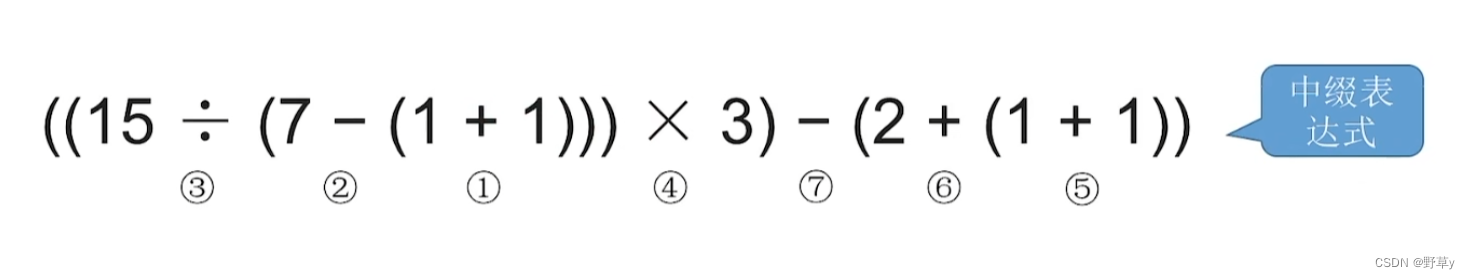转换成后缀表式:          15 7 11+ - / 3 *  2 11 + + -

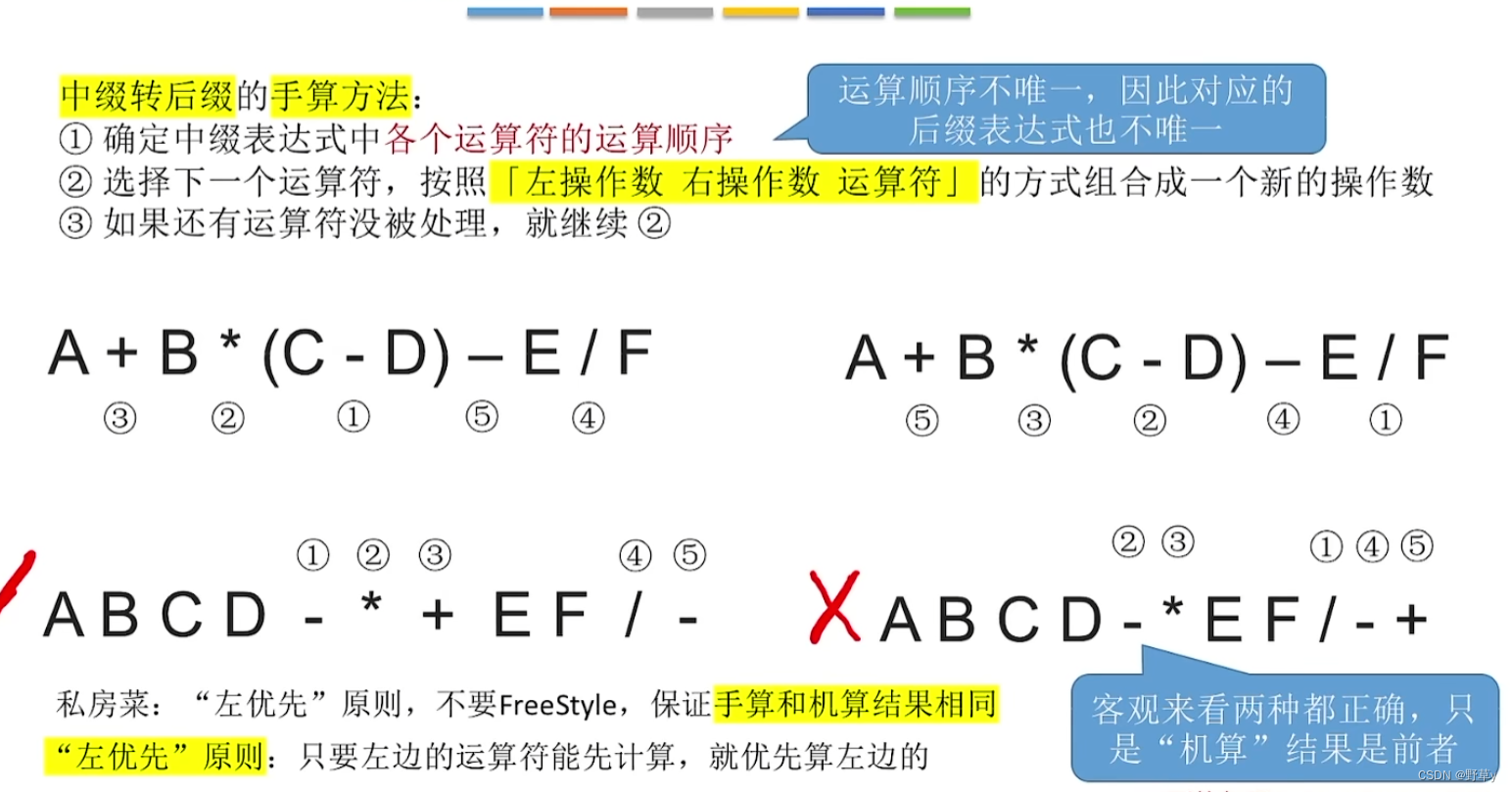
"左优先"原则：只要左边的运算符能先计算，就优先计算左边的（可保证运算唯一）

中缀表达式转后缀表达式(机算)

代码示例：

要将中缀表达式转换为后缀表达式，可以按照以下步骤进行：

1. 初始化一个空栈，用于保存暂时还不能确定运算顺序的运算符。
2. 初始化一个空字符串，用于保存最终的后缀表达式。
3. 从左到右扫描中缀表达式中的每个字符。
4. 对于每个字符，执行以下操作：
   • 如果是操作数，直接添加到后缀表达式中。
   • 如果是左括号 (，将其压入栈中。
   • 如果是右括号 )，则弹出栈中的运算符并添加到后缀表达式中，直到遇到对应的左括号 (。左括号 ( 弹出但不添加到后缀表达式中。
   • 如果是运算符（如 +、-、*、/ 等），则将栈中所有优先级高于或等于当前运算符的运算符弹出并添加到后缀表达式中。然后将当前运算符压入栈中。
5. 扫描完中缀表达式后，将栈中剩余的运算符全部弹出并添加到后缀表达式中。

下面是一个C语言的示例代码，用于将中缀表达式转换为后缀表达式：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>#define MAX_SIZE 100// 栈的结构定义
typedef struct {char items[MAX_SIZE];int top;
} Stack;// 初始化栈
void initStack(Stack* stack) {stack->top = -1;
}// 判断栈是否为空
int isEmpty(Stack* stack) {return stack->top == -1;
}// 判断栈是否满
int isFull(Stack* stack) {return stack->top == MAX_SIZE - 1;
}// 压栈
void push(Stack* stack, char value) {if (isFull(stack)) {printf("Error: Stack is full.\n");return;}stack->items[++stack->top] = value;
}// 出栈
char pop(Stack* stack) {if (isEmpty(stack)) {printf("Error: Stack is empty.\n");return '\0';}return stack->items[stack->top--];
}// 获取栈顶元素
char peek(Stack* stack) {if (isEmpty(stack)) {printf("Error: Stack is empty.\n");return '\0';}return stack->items[stack->top];
}// 操作符优先级
int precedence(char op) {if (op == '+' || op == '-') {return 1;} else if (op == '*' || op == '/') {return 2;} else if (op == '(' || op == ')') {return 0;}return -1;
}// 中缀转后缀
void infixToPostfix(char* infix, char* postfix) {Stack stack;initStack(&stack);int i, j;for (i = 0, j = 0; infix[i] != '\0'; ++i) {if (infix[i] == ' ') continue;else if (isdigit(infix[i]) || isalpha(infix[i])) {postfix[j++] = infix[i];} else if (infix[i] == '(') {push(&stack, infix[i]);} else if (infix[i] == ')') {while (!isEmpty(&stack) && peek(&stack) != '(') {postfix[j++] = pop(&stack);}pop(&stack); // 弹出左括号} else {while (!isEmpty(&stack) && precedence(infix[i]) <= precedence(peek(&stack))) {postfix[j++] = pop(&stack);}push(&stack, infix[i]);}}while (!isEmpty(&stack)) {postfix[j++] = pop(&stack);}postfix[j] = '\0'; // 结束字符串
}int main() {char infix[] = "a+b*(c-d)-e/f";char postfix[MAX_SIZE];infixToPostfix(infix, postfix);printf("Infix: %s\n", infix);printf("Postfix: %s\n", postfix);return 0;
}

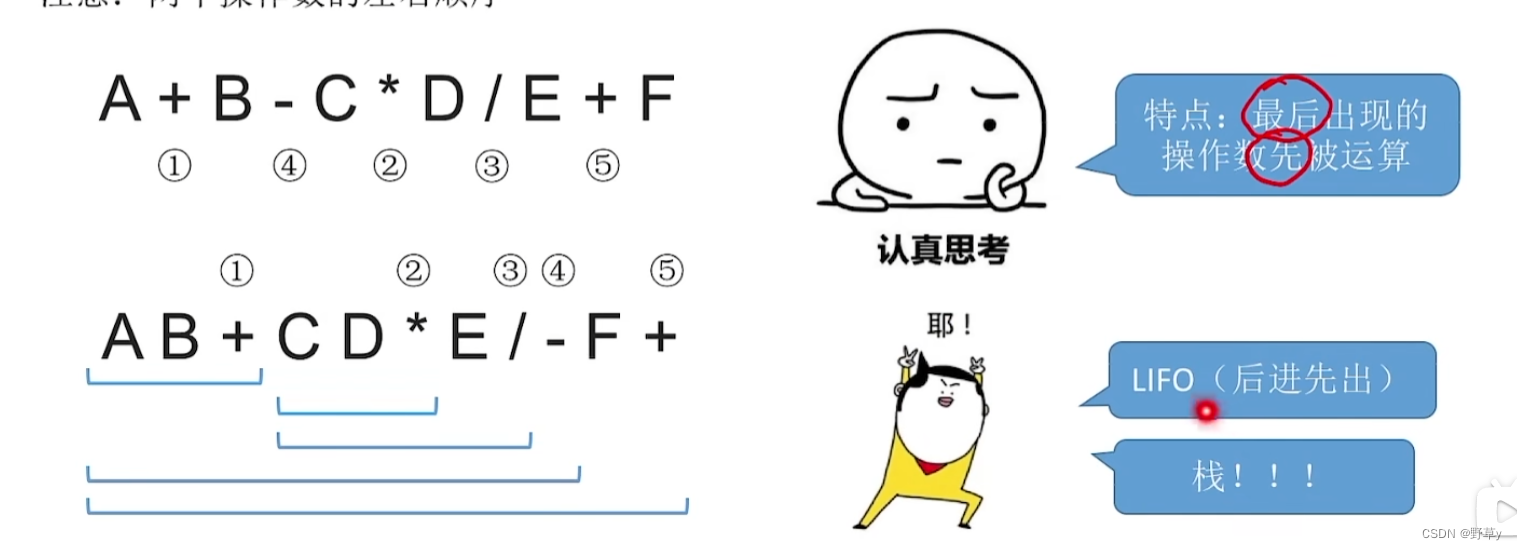
后缀表达式的计算(手算)

从左往右扫描，每遇到一个运算符，就让运算符前面最近的两个操作数执行对应运算，合体为一个操作数

注意：两个操作数的左右顺序

后缀表达式的计算(机算)

用栈实现后缀表达式的计算：

1. 从左往右扫描下一个元素，直到处理完所以元素
2. 若扫描到操作数则压入栈，并回到1；否则执行3
3. 若扫描到运算符，则弹出两个栈顶元素，执行相应运算，运算结果压回栈顶,回到1

注意：后缀表达式先弹出的元素是‘右操作数’

入栈流程：

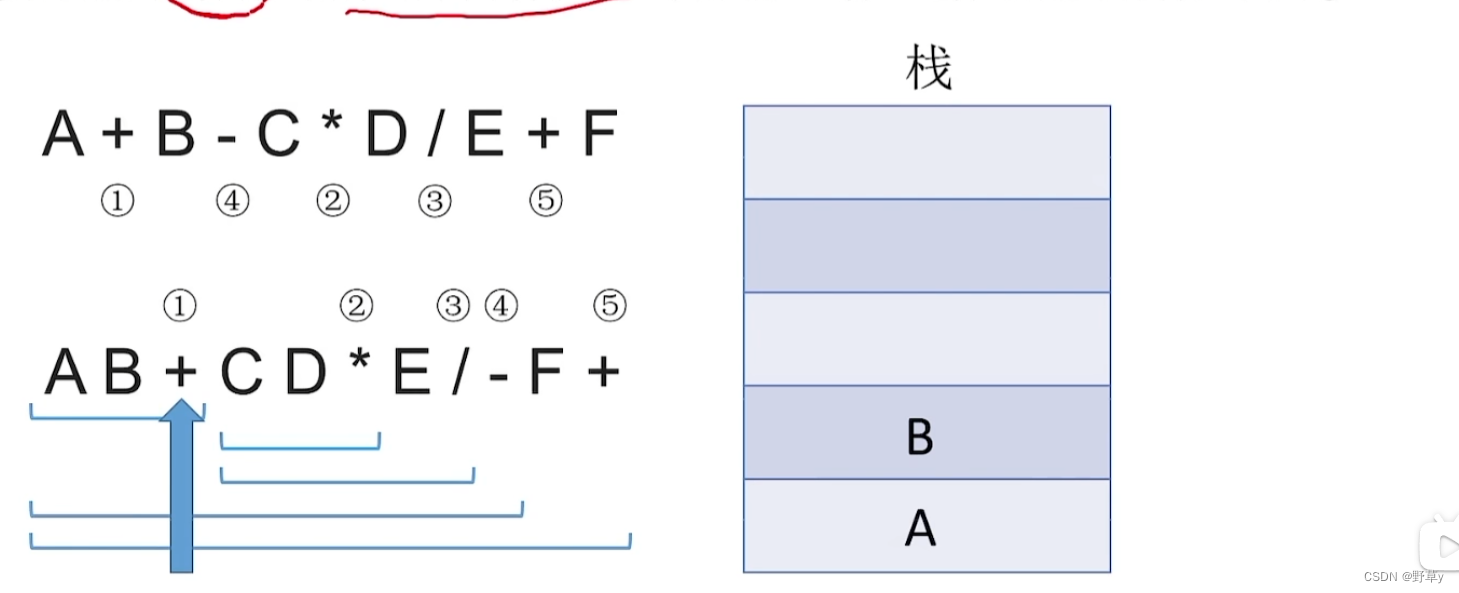
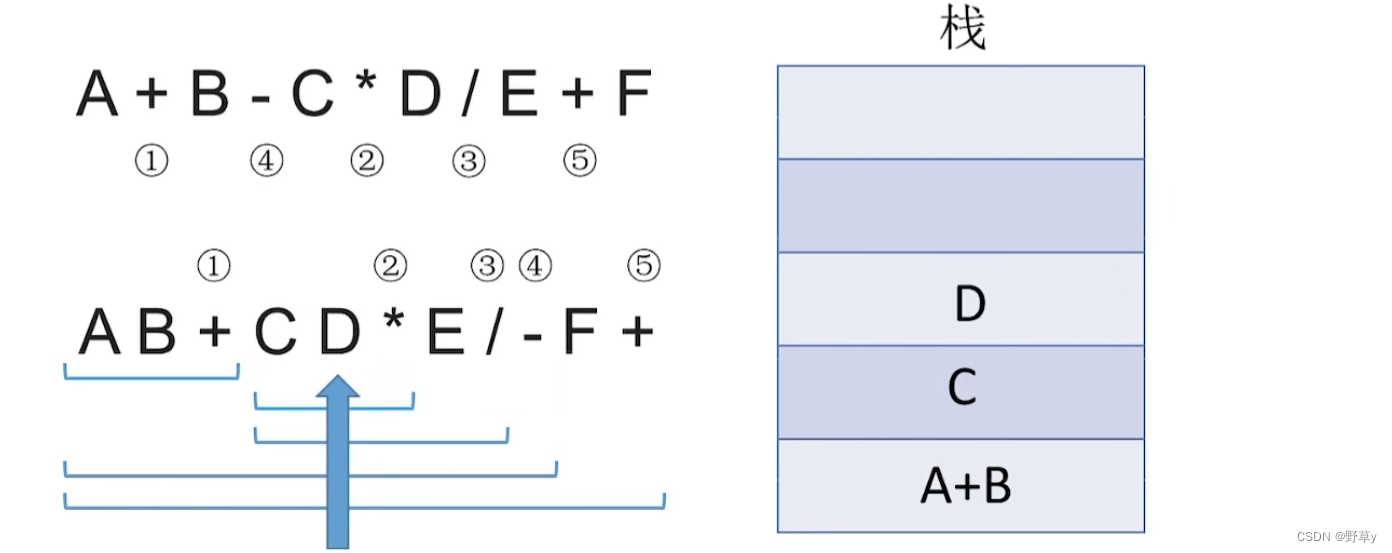
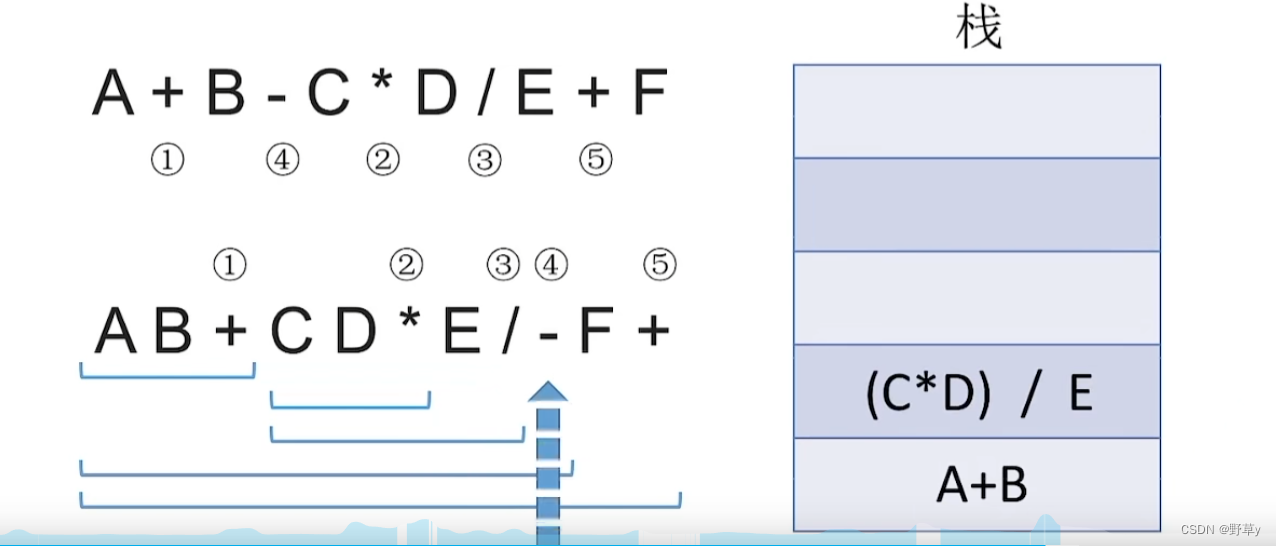
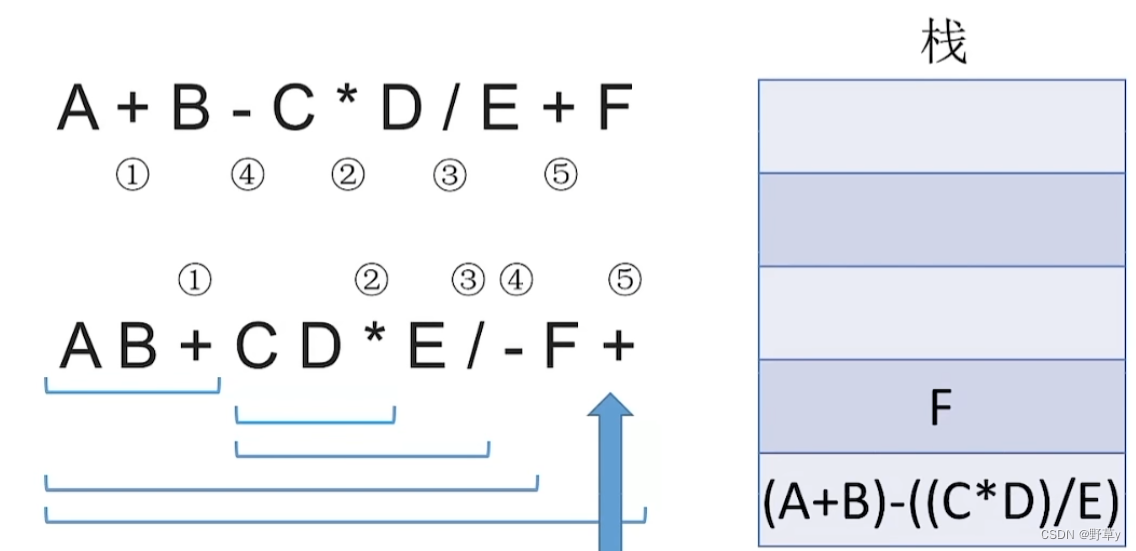
 中缀表达式转前缀表达式(手算)

1. 确定中缀表达式中各个运算符的运算顺序
2. 确定下一个运算符，按照[运算符 左操作数 右操作数]的方式组合成一个新的操作数
3. 如果还有运算符没被处理，就继续2

"右优先"原则:只要右边的运算符能先计算，就优先算右边的

前缀表达式的计算

1. 从右往左扫描下一个元素，直到处理完所有元素
2. 若扫描到操作数则压入栈，并回到1；否则执行3
3. 若扫描到运算符，则弹出两个栈顶元素，执行相应运算，运算结构压回栈顶，回到1

注意前缀表达式先弹出的元素是‘左操作数’

栈在递归中的应用

递归调用时，函数调用栈可称为“递归工作栈”

每进入一层递归，就将递归调用所需信息压入栈顶

每退出一层递归，就从栈顶弹出相应信息

• 缺点:太多层递归可能会导致栈溢出

• 

递归算法可能会包含很多重复计算 

总结