SMU Summer 2024 Contest Round 3
A.Hcode OnlineJudge
先用欧拉筛把质数预处理出来,然后枚举左端点的质数,只需要询问右端点是不是质数并取差值的min就行了
#include<bits/stdc++.h>
#define endl '\n'
#define mk make_pair
#define int long long
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 1e6+10;
int n,m,k;vector<int>pri;
bool su[10005];void get(){for(int i=2;i<=10000;i++){if(!su[i]) pri.push_back(i);for(auto ed:pri){if(i*ed>10005) break;su[ed*i]=1;if(i%ed==0) {break;}}}
}void sovle(){get();while(scanf("%d",&n)!=EOF){int ans1=0,ans2=0,num=1000000;for(auto ed:pri){if(!su[abs(n-ed)]){int vd=abs(n-ed);if(abs(ed-vd)<num){num=abs(ed-vd);ans1=min(ed,vd);ans2=max(ed,vd);}}}cout<<ans1<<" "<<ans2<<endl;}
}signed main()
{ //ios::sync_with_stdio(false), cin.tie(0),cout.tie(0); int t = 1; //cin>>t;while (t --){sovle();}return 0;
}
B.Hcode OnlineJudge
随便模拟一下就找到规律了(被多组数据狠狠教育了
#include<bits/stdc++.h>
#define endl '\n'
#define mk make_pair
#define int long long
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 1e6+10;
int n,m,k;void sovle(){while(scanf("%d %d",&n,&m)){if(!n&&!m) return;cout<<n+m-2<<endl;}
}signed main()
{ ios::sync_with_stdio(false), cin.tie(0),cout.tie(0); int t = 1; //cin>>t;while (t --){sovle();}return 0;
}
C.Hcode OnlineJudge
要使疲劳度最小,必然要找k组相邻的最小差值对,考虑n方的dp,i,j表示前i个物品取k对,注意考虑怎么初始化
#include<bits/stdc++.h>
#define endl '\n'
#define mk make_pair
#define int long long
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 1e6+10;
const int inf = 0x3f3f3f3f;
int n,m,k;int f(int x,int y){return (x-y)*(x-y);
}void sovle(){while(cin>>n>>k){int a[n+1];for(int i=1;i<=n;i++) cin>>a[i];sort(a+1,a+n+1);int dp[n+1][k+1];for(int i=0;i<=n;i++){for(int j=0;j<=k;j++){if(i==0||j==0) dp[i][j]=0;else dp[i][j]=inf;}}for(int i=2;i<=n;i++){for(int j=1;j*2<=i&&j<=k;j++){dp[i][j]=min(dp[i-1][j],dp[i-2][j-1]+f(a[i-1],a[i]));}}cout<<dp[n][k]<<endl;}
}signed main()
{ ios::sync_with_stdio(false), cin.tie(0),cout.tie(0); int t = 1; //cin>>t;while (t --){sovle();}return 0;
}
D.Hcode OnlineJudge
水题
#include<bits/stdc++.h>
#define endl '\n'
#define mk make_pair
#define int long long
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 1e6+10;
int n,m,k;void sovle(){int sum=0;cin>>n;vector<int>a(n);for(int i=0;i<n;i++) {cin>>a[i];if(a[i]>10) sum+=a[i]-10;}cout<<sum<<endl;
}signed main()
{ ios::sync_with_stdio(false), cin.tie(0),cout.tie(0); int t = 1; //cin>>t;while (t --){sovle();}return 0;
}
F.Hcode OnlineJudge
对于每组,只有取左边或者右边,等同于对左边,取或者不取。数据范围很小,二进制枚举秒了
#include<bits/stdc++.h>
#define endl '\n'
#define mk make_pair
#define int long long
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 1e6+10;
int n,m,k;void sovle(){cin>>n>>m;vector<int>a(m),b(m);for(int i=0;i<m;i++) cin>>a[i]>>b[i];cin>>k;vector<int>c(k),d(k);int max1=-1;for(int i=0;i<k;i++) cin>>c[i]>>d[i];for(int i=0;i<(1<<k);i++){map<int,int>v,x;for(int j=0;j<k;j++){if((i>>j)&1){v[c[j]]=1;}else{v[d[j]]=1;}}int sum=0;for(int i=0;i<m;i++){if(v[a[i]]&&v[b[i]]){sum++;}}max1=max(max1,sum);}cout<<max1<<endl;
}signed main()
{ ios::sync_with_stdio(false), cin.tie(0),cout.tie(0); int t = 1; //cin>>t;while (t --){sovle();}return 0;
}
I.Hcode OnlineJudge
给一个小于1e18的正整数,询问能否通过删除最少的位数让该数被3整除。类似的,二进制枚举当前位数删或者不删
#include<bits/stdc++.h>
#define endl '\n'
#define mk make_pair
#define int long long
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 1e6+10;
int n,m,k;void sovle(){string s;cin>>s;int n=s.size();int num=-1;for(int i=0;i<(1<<n);i++){map<int,int>v;for(int j=0;j<n;j++){if((i>>j)&1){v[j]=1;}}int u=0;int x=1;int sum=0;for(int i=n-1;i>=0;i--){if(v[n-1-i]) {sum++;continue;}u+=x*(s[i]-'0');x*=10;}if(u%3==0&&u){if(num==-1) num=sum;else num=min(sum,num);}}cout<<num<<endl;
}signed main()
{ ios::sync_with_stdio(false), cin.tie(0),cout.tie(0); int t = 1; //cin>>t;while (t --){sovle();}return 0;
}
相关文章:

SMU Summer 2024 Contest Round 3
A.Hcode OnlineJudge 先用欧拉筛把质数预处理出来,然后枚举左端点的质数,只需要询问右端点是不是质数并取差值的min就行了 #include<bits/stdc.h> #define endl \n #define mk make_pair #define int long long using namespace std; typedef lon…...

uniapp 封装瀑布流组件
思路: 1.coulumns:需要分成几列 2.如何分布数据 3.计算每列的宽度 4.图片进行高度自适应 <template><view :style"{ margin: boxM }"><view class"flex flex-justify-start bg-red" style"background-colo…...

pd虚拟机去虚拟化是什么意思?pd虚拟机去虚拟化教程 PD虚拟机优化设置
Parallels Desktop for Mac(PD虚拟机)去虚拟化是指在虚拟机(Virtual Machine,简称 VM)中禁用或减少虚拟化层的影响,使其表现更接近于物理机。这种操作通常用于提高虚拟机的性能或解决某些软件兼容性问题。具…...

低代码研发项目管理流程优化:提效与创新的双重驱动
随着信息技术的迅猛发展,软件项目的规模和复杂度日益增加,传统的软件开发方式已经难以满足快速迭代和高效交付的需求。在这一背景下,低代码平台应运而生,以其高效、灵活、易用的特点,迅速成为软件行业的新宠。然而&…...
32位版 C 库函数time 将在 2038 年溢出,那到时候,它该何去何从
简单地说,通常不必担心,在64位操作系统已经成为主流的今天这基本上不是问题(在写这篇回答的时候,我才发现我甚至找不到32位的机器来测试)刚好我有一些资料,是我根据网友给的问题精心整理了一份「32库函数的…...

C语言 printf函数缓冲机制
printf不立即打印到stdout的原因 printf函数使用了缓冲机制。当我们调用printf时,输出通常不会立即显示在屏幕上,而是先存储在一个缓冲区中。这是为了提高I/O操作的效率。 缓存数据输出的原理 stdio库维护了一个缓冲区。当缓冲区满了,或者在特定条件下,缓冲区的内容会被刷新…...

【Linux进阶】文件系统8——硬链接和符号连接:ln
在Linux下面的链接文件有两种, 一种是类似Windows的快捷方式功能的文件,可以让你快速地链接到目标文件(或目录);另一种则是通过文件系统的inode 链接来产生新文件名,而不是产生新文件,这种称为硬链接&…...
、dijkstra朴素版)
代码随想录算法训练营Day64|拓扑排序(卡码网117)、dijkstra朴素版
拓扑排序 117. 软件构建 (kamacoder.com) 拓扑排序简单的说是将一个有向图转为线性的排序。 它将图中的所有结点排序成一个线性序列,使得对于任何的边uv,结点u在序列中都出现在结点v之前,这样的序列满足图中所有的前驱-后继关系。 拓扑排…...

neo4j 图数据库:Cypher 查询语言、医学知识图谱
neo4j 图数据库:Cypher 查询语言、医学知识图谱 Cypher 查询语言创建数据查询数据查询并返回所有节点查询并返回所有带有特定标签的节点查询特定属性的节点及其所有关系和关系的另一端节点查询从名为“小明”的节点到名为“小红”的节点的路径 更新数据更新一个节点…...

数据结构基础--------【二叉树基础】
二叉树基础 二叉树是一种常见的数据结构,由节点组成,每个节点最多有两个子节点,左子节点和右子节点。二叉树可以用来表示许多实际问题,如计算机程序中的表达式、组织结构等。以下是一些二叉树的概念: 二叉树的深度&a…...

数据开源 | Magic Data大模型高质量十万轮对话数据集
能够自然的与人类进行聊天交谈,是现今的大语言模型 (LLM) 区别于传统语言模型的重要能力之一,近日OpenAI推出的GPT-4o给我们展示了这样的可能性。 对话于人类来说是与生俱来的,但构建具备对话能力的大模型是一项不小的挑战,收集高…...

webpack之ts打包
tsconfig.json配置 // 是否对js文件进行编译,默认false"allowJs": true,// 是否检查js代码是否符合语法规范,默认false(引入的外部文件有可能语法有问题)"checkJs": true, allowJs和checkJs基本是同时出现,因为有了allowJs 这个检查…...

MATLAB数据统计描述和分析
描述性统计就是搜集、整理、加工和分析统计数据, 使之系统化、条理化,以显示出数据资料的趋势、特征和数量关系。它是统计推断的基础,实用性较强,在数学建模的数据描述部分经常使用。 目录 1.频数表和直方图 2 .统计量 3.统计…...
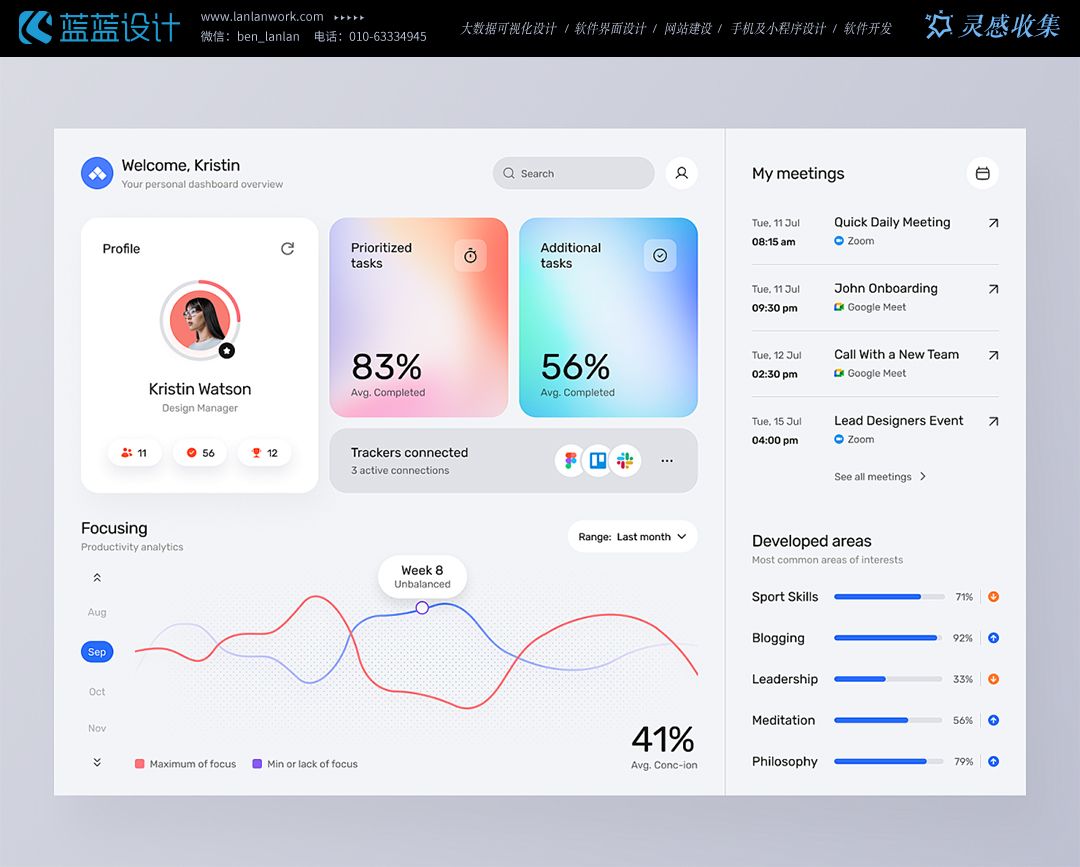
设计分享—国外后台界面设计赏析
国外后台界面设计将用户体验放在首位,通过直观易懂的布局和高效的交互设计,提升用户操作效率和满意度。 设计不仅追求美观大方,还注重功能的实用性和数据的有效展示,通过图表和图形化手段使数据更加直观易懂。 采用响应式布局&a…...
)
最小生成树(算法篇)
算法之最小生成树 最小生成树 概念: 最小生成树是一颗连接图G所有顶点的边构成的一颗权最小的树,最小生成树一般是在无向图中寻找。最小生成树共有N-1条边(N为顶点数)。 算法: Prim算法 概念: Prim(普里姆)算法是生成最小生…...
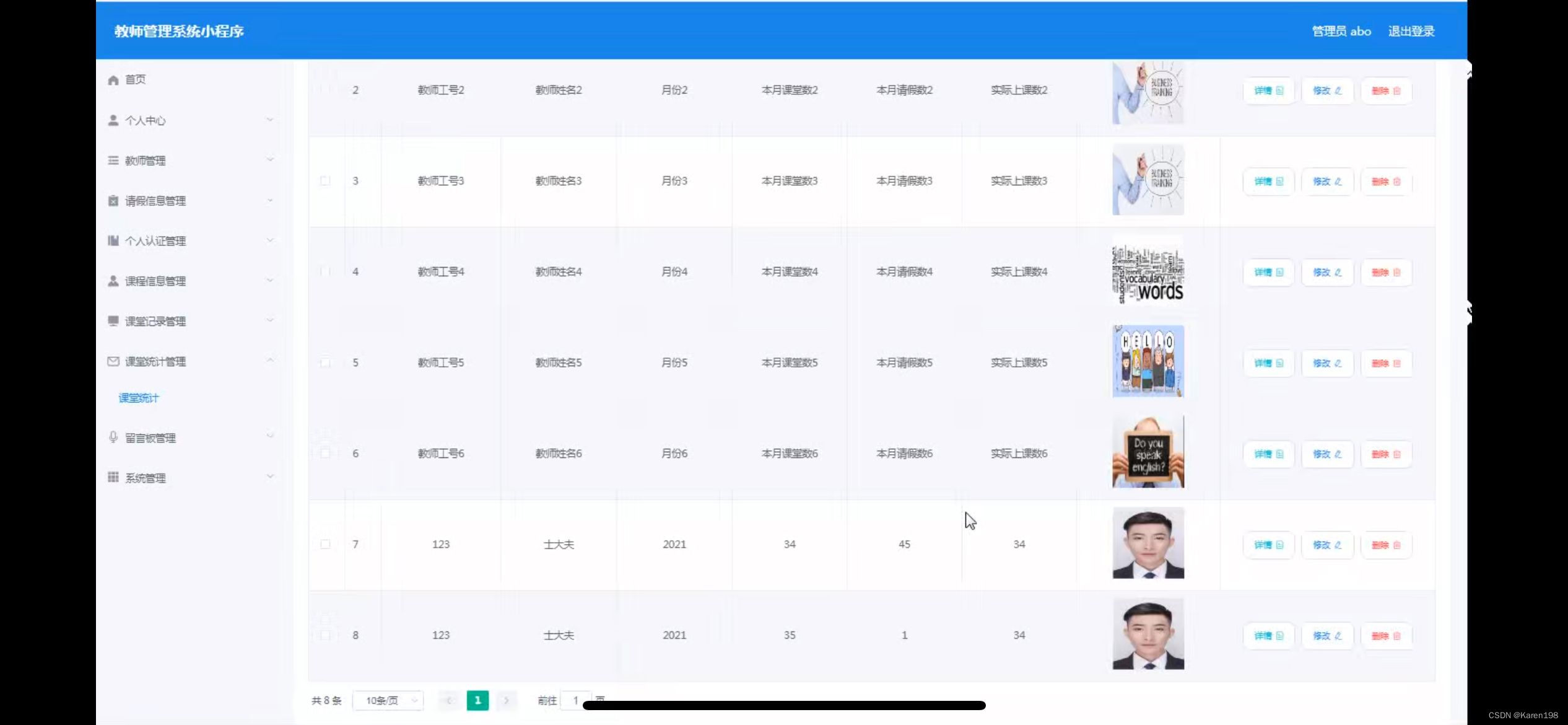
教师管理小程序的设计
管理员账户功能包括:系统首页,个人中心,教师管理,个人认证管理,课程信息管理,课堂记录管理,课堂统计管理,留言板管理 微信端账号功能包括:系统首页,课程信息…...

Selenium 等待
环境: Python 3.8 selenium3.141.0 urllib31.26.19 Chromium 109.0.5405.0 (32 位) # 1 固定等待(time) # 固定待是利用python语言自带的time库中的sleep()方法,固定等待几秒。 # 这种方式会导致这个脚本运…...

安装easy-handeye
一、aruco_ros配置 mkdir -p ~/ros_ws/src cd ~/ros_ws/src git clone -b melodic-devel https://github.com/pal-robotics/aruco_ros.git cd .. catkin_make 二、visp配置(需要联外网下载东西,不然会一直出问题) sudo apt-get install ros-melodic-…...
)
【面试题】MySQL 索引(第二篇)
1.索引 索引是数据库中的一个核心概念,它对于提高数据库查询效率至关重要。以下是索引的详细概念解析: 一、索引的定义 基本定义:索引是一个排序的列表,其中存储着索引的值和包含这些值的数据所在行的物理地址(或逻…...

4. 小迪安全v2023笔记 javaEE应用
4. 小迪安全v2023笔记 javaEE应用 大体上跟随小迪安全的课程,本意是记录自己的学习历程,不能说是完全原创吧,大家可以关注一下小迪安全。 若有冒犯,麻烦私信移除。 默认有java基础。 文章目录 4. 小迪安全v2023笔记 javaEE应…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...
