今天是国际数学日,既是爱因斯坦的生日又是霍金的忌日

目录
一、库函数计算 π
二、近似值计算 π
三、无穷级数计算 π
四、割圆术计算 π
五、蒙特卡罗法计算 π
六、计算800位精确值
从2020年开始,每年的3月14日又被定为国际数学日,是2019年11月26日联合国教科文组织第四十届大会上正式宣布的。巧合的是这一天既是爱因斯坦的生日,又是霍金的忌日,两位物理界的巨擘一个出生于(1879)另一个离世于(2018)这个日子。
以前,3月14日还是一年一度的庆祝常数π的节日,由圆周率最常用的近似值3.14而来,称为圆周率日(π Day)。
圆周率(π)是圆的周长与直径的比值,一般用希腊字母π表示,是一个在数学及物理学中普遍存在的数学常数。π也等于圆形之面积与半径平方之比,是精确计算圆周长、圆面积、球体积等几何形状的关键值。
公元263年,中国数学家刘徽用“割圆术”计算圆周率,他先从圆内接正六边形,逐次分割一直算到圆内接正192边形,给出π=3.141024的圆周率近似值。他说:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣。”这包含了求极限的思想。
公元480年左右,南北朝时期的数学家祖冲之进一步得出精确到小数点后7位的结果,给出不足近似值3.1415926和过剩近似值3.1415927,还得到两个近似分数值,密率355/113和约率22/7。密率是个很好的分数近似值,要取到才能得出比略准确的近似。在之后的800年里祖冲之计算出的π值都是最准确的。
计算机的出现使π值计算有了突飞猛进的发展。经吉尼斯世界纪录认证,目前π的最准确值,超过小数点后62,831,853,071,796位。
今天来用python代码来算算圆周率 π,也算比较应景的。方法有很多,列举几个如下:
一、库函数计算 π
>>> import math
>>> math.pi
3.141592653589793
>>> math.acos(-1)
3.141592653589793
>>> math.atan(1)*4
3.141592653589793
>>> math.atan2(2,2)*2*2
3.141592653589793二、近似值计算 π
>>> print(22/7)
3.142857142857143
>>> print(355/113)
3.1415929203539825
>>> print(102573/32650)
3.141592649310873
>>> import math
>>> print(16*math.atan(1/5)-4*math.atan(1/239))
3.1415926535897936
>>> print(32*math.atan(1/10)-4*math.atan(1758719/147153121))
3.1415926535897936
>>> math.pi #比对
3.141592653589793三、无穷级数计算 π
π/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + 1/13 - 1/15 ...
pi=0
for i in range(1,10000000):pi+=0.5/(i**2-i+0.1875)print(pi)'''
3.1415926035880934
>>>
'''π = 3 + 4/(2*3*4) - 4/(4*5*6) + 4/(6*7*8) - 4/(8*9*10) + 4/(10*11*12) - 4/(12*13*14) ...
pi=3
for i in range(2,10000000,4):pi+=4/(i*(i+1)*(i+2))-4/((i+2)*(i+3)*(i+4))print(pi)'''
3.1415926535895253
>>>
'''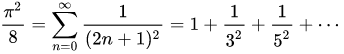
from math import sqrt
pi=0
for i in range(1,10000000,2):pi+=1/(i*i)print(sqrt(8*pi))'''
3.141592589927253
>>>
'''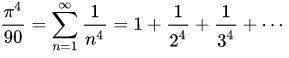
from math import sqrt
pi=0
for i in range(1,10000000):pi+=1/(i**4)print(sqrt(sqrt(90*pi)))'''
3.141592653589592
>>>
'''
印度天才数学家拉马努金1914年发表了一个圆周率计算公式,每计算一项可以得到8位的十进制精度;以上公式由Jonathan Borwein和Peter Borwein兄弟俩在1987年用基于椭圆积分变换的理论给出证明并改良过后的公式。
from math import sqrt
from math import factorialfor j in range(1,6):pi=0for i in range(j):pi+= (26390*i+1103)*factorial(4*i)/(factorial(i)**4)/(396**(4*i))print("%.20f"%(1/(2*sqrt(2)*pi/9801)))'''
3.14159273001330552333
3.14159265358979400418
3.14159265358979311600
3.14159265358979311600
3.14159265358979311600
>>>
'''以上代码算到第三项就到精度极限了,应该是python本身精度不够引起的。
四、割圆术计算 π
割圆术:古代(魏晋)数学家刘徽 公元263年《九章算术注》记载,现代数学用三角函数来表示分割的三角形面积,如下切割3亿份就能得到15位精度

>>> from math import sin
>>> sin(2*math.pi/300000000)*300000000/2
3.141592653589793五、蒙特卡罗法计算 π
方法:单位圆外接一个正方形,然后向其中随机撒点,通过计算落在圆内的点数与总点数之比计算圆周率。以圆心为原点坐标,计算点与原点的距离,距离不于1的有效点数 hits 增一。
from random import randomDots = 2000000for j in range(5):hits = 0for i in range(Dots):x,y = random(),random()dist = (x**2+y**2)**0.5if dist <= 1.0:hits+=1pi = 4 * (hits/Dots)print(pi)每次计算距离有三次 ** 运算,所以速度有点慢;精度也不高,200万个点能得出 3.14 两位精度。
六、计算800位精确值
a,c=10000,2800
b=e=0
f=[0]*2801
while b!=c:f[b]=a//5b+=1
while c!=0:d=0g=c*2b=cwhile 1:d+=f[b]*ag-=1f[b]=d%gd//=gg-=1b-=1if b!=0:d*=belse:breakc-=14print('%.4d'%(e+d//a),end='')e=d%a这段代码比较神奇的,以前我写过关于此的文章,请见:http://t.csdn.cn/5oEAA
回过来,作为一名数学爱好者,再次庆祝一下这个数学节日,也算符合教科文组织确立本纪念日的目的:“为庆祝数学在生活中的美丽和重要性”。最后,让我们来共同欣赏一下 π 的独特魅力:

莱布尼茨级数

平方数倒数之和无穷级数
 欧拉恒等式——5个常量构成“最美公式”,有理数无理数实数虚数融汇一体
欧拉恒等式——5个常量构成“最美公式”,有理数无理数实数虚数融汇一体

双曲几何三角形面积公式
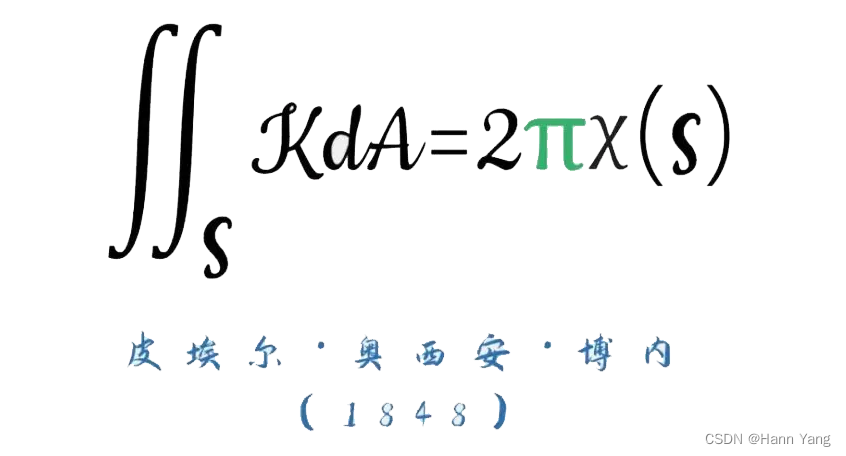
高斯-博内定理

等周不等式

拉马努金“最丑”的数学公式

爱因斯坦广义相对论的核心方程:爱因斯坦场方程

海森堡不确定性原理是量子力学的一个重要原理
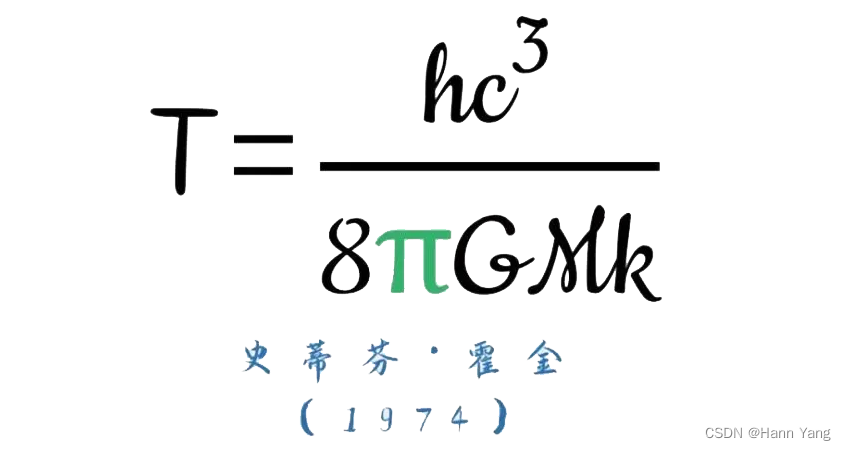 霍金黑洞温度公式,除了有pi还包含了牛顿的万有引力常数(G)、普朗克常数(h)、光速(c)、以及玻尔兹曼常数(k)
霍金黑洞温度公式,除了有pi还包含了牛顿的万有引力常数(G)、普朗克常数(h)、光速(c)、以及玻尔兹曼常数(k)
相关文章:
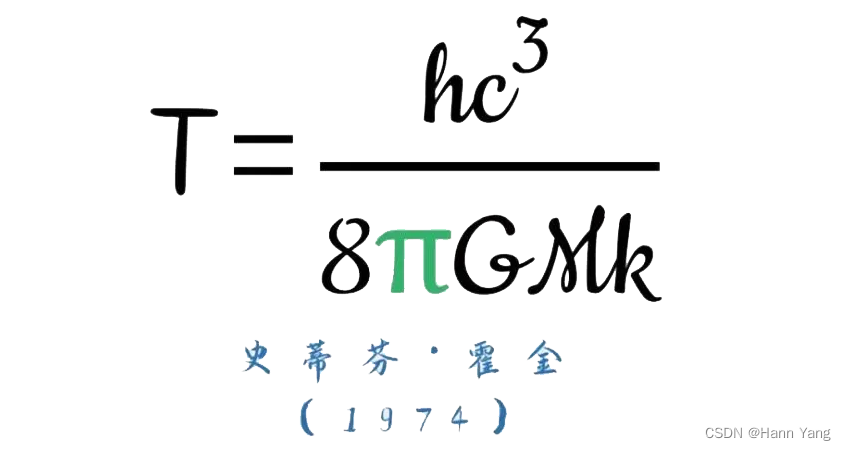
今天是国际数学日,既是爱因斯坦的生日又是霍金的忌日
目录 一、库函数计算 π 二、近似值计算 π 三、无穷级数计算 π 四、割圆术计算 π 五、蒙特卡罗法计算 π 六、计算800位精确值 从2020年开始,每年的3月14日又被定为国际数学日,是2019年11月26日联合国教科文组织第四十届大会上正式宣布…...

Qt Quick - StackLayout 堆布局
StackLayout 堆布局一、概述二、attached 属性三、例子1. 按钮切换 StackLayout 页面一、概述 StackLayout 其实就是说,在同一个时刻里面,只有一个页面是展示出来的,类似QStackWidget 的功能,主要就是切换界面的功能。这个类型我…...
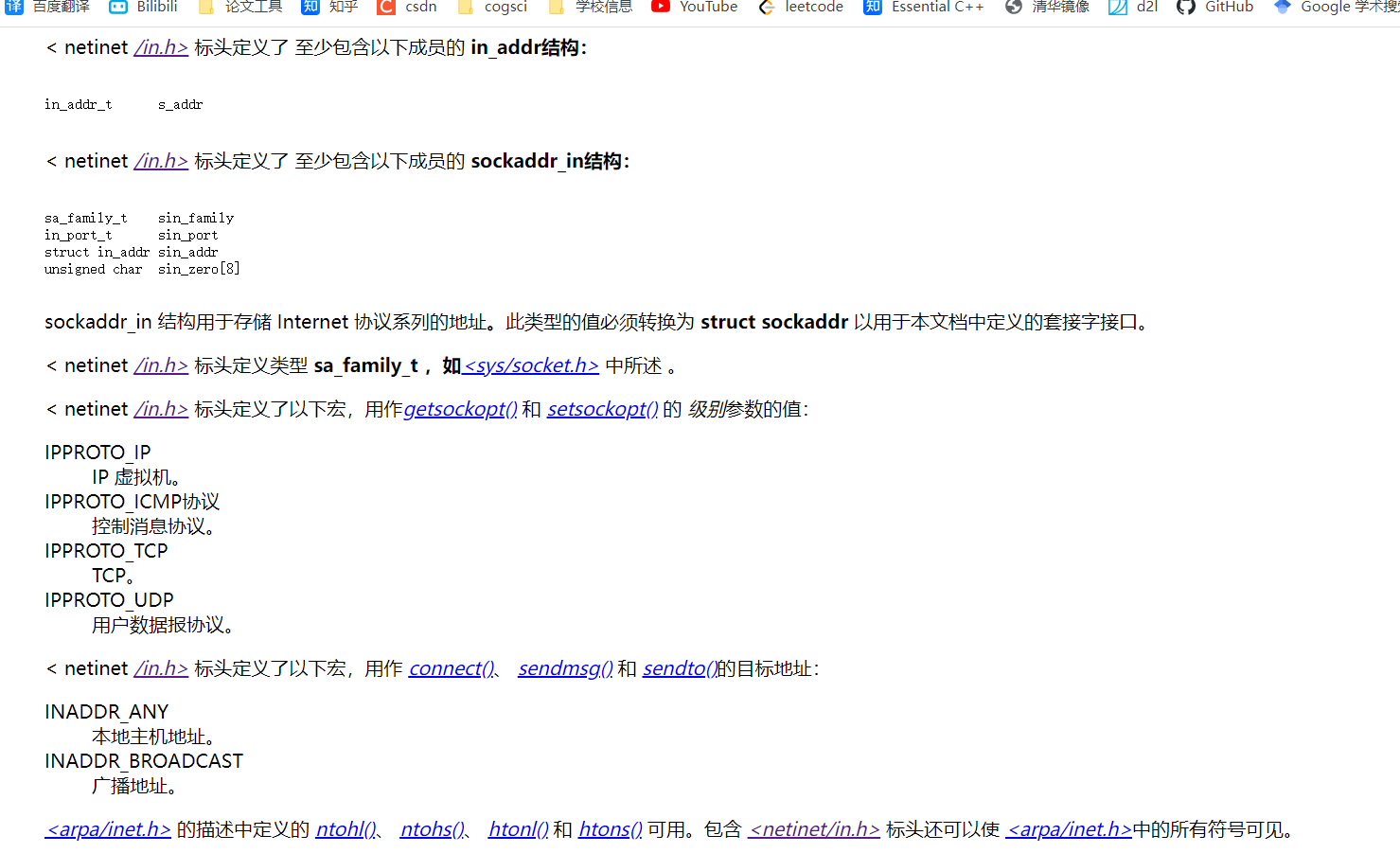
C/C++网络编程笔记Socket
https://www.bilibili.com/video/BV11Z4y157RY/?vd_sourced0030c72c95e04a14c5614c1c0e6159b上面链接是B站的博主教程,源代码来自上面视频,侵删,这里只是做笔记,以供复习和分享。上一篇博客我记录了配置环境并且跑通了࿰…...

RK3568平台开发系列讲解(网络篇)什么是Socket套接字
🚀返回专栏总目录 文章目录 一、什么是socket ?二、socket 理解为电话机三、socket 的发展历史四、套接字地址格式4.1、通用套接字地址格式4.2、IPv4 套接字格式地址4.3、IPv6 套接字地址格式4.4、几种套接字地址格式比较沉淀、分享、成长,让自己和他人都能有所收获!😄 …...
网络安全竞赛试题——渗透测试解析(详细))
2022年全国职业院校技能大赛(中职组)网络安全竞赛试题——渗透测试解析(详细)
渗透测试 任务环境说明: 服务器场景:Server9服务器场景操作系统:未知(关闭连接)系统用户名:administrator密码:123456通过本地PC中渗透测试平台Kali对靶机场景进行系统服务及版本扫描渗透测试,以xml格式向指定文件输出信息(使用工具Nmap),将以xml格式向指定文件输出…...

尚融宝03-mybatis-plus基本CRUD和常用注解
目录 一、通用Mapper 1、Create 2、Retrieve 3、Update 4、Delete 二、通用Service 1、创建Service接口 2、创建Service实现类 3、创建测试类 4、测试记录数 5、测试批量插入 三、自定义Mapper 1、接口方法定义 2、创建xml文件 3、测试条件查询 四、自定义Serv…...

vue多行显示文字展开
这几天项目里面有一个需求,多行需要进行展开文字,类似实现这种效果 难点就在于页面布局 一开始就跟无头苍蝇似的,到处百度 ,后面发现网上的都不适合自己,最终想到了解决方案 下面是思路: 需求是超过3行&a…...
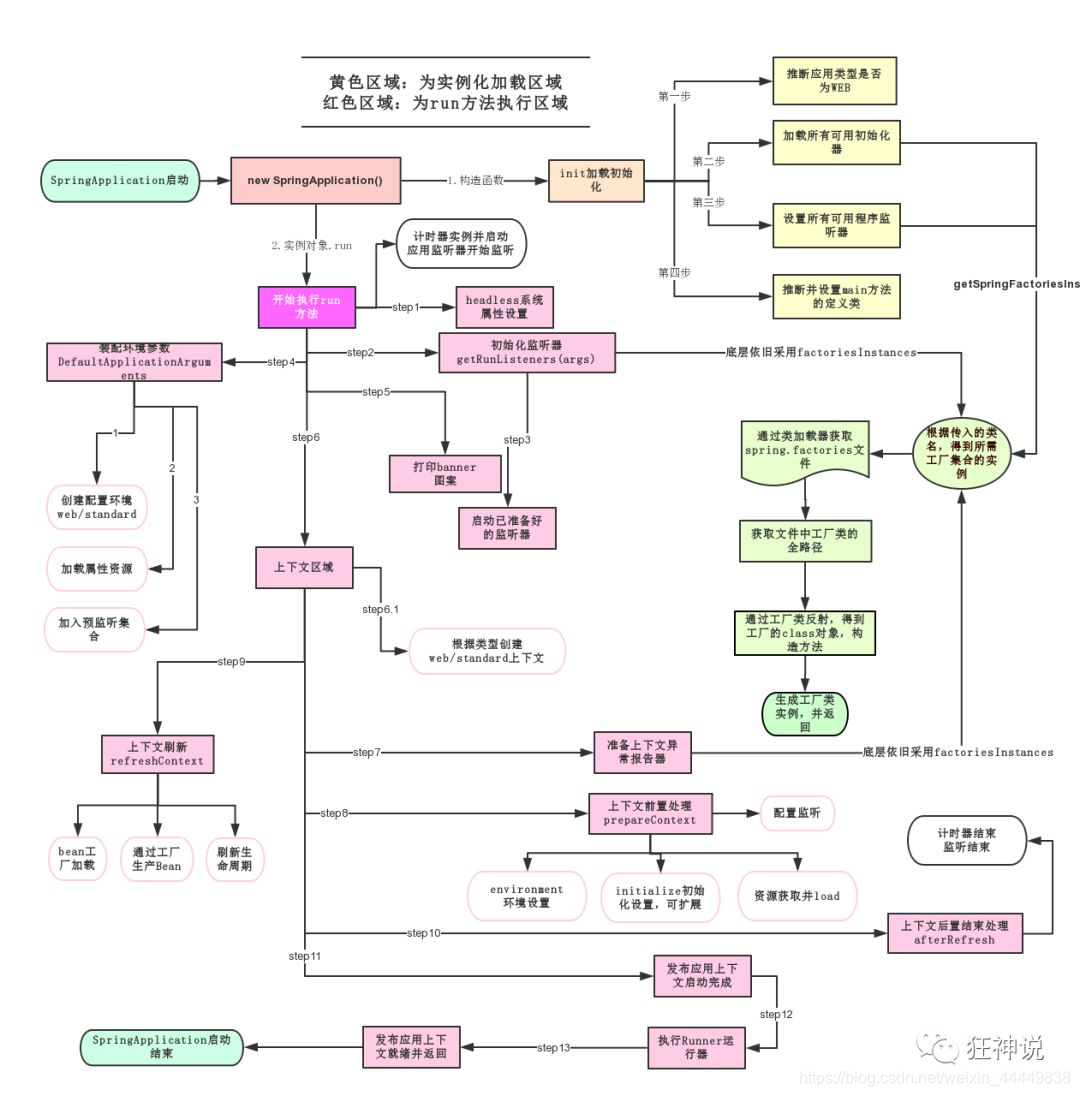
SpringBoot:SpringBoot 的底层运行原理解析
声明原文出处:狂神说 文章目录1. pom.xml1 . 父依赖2 . 启动器 spring-boot-starter2. 主启动类的注解1. 默认的主启动类2. SpringBootApplication3. ComponentScan4. SpringBootConfiguration5. SpringBootApplication 注解6. spring.factories7. 结论8. 简单图解3…...

哪些场景会产生OOM?怎么解决?
文章目录 堆内存溢出方法区(运行时常量池)和元空间溢出直接内存溢出栈内存溢出什么时候会抛出OutOfMemery异常呢?初看好像挺简单的,其实深究起来考察的是对整个JVM的了解,而这个问题从网上可以翻到一些乱七八糟的答案,其实在总结下来基本上4个场景可以概括下来。 堆内存溢出…...

金三银四、金九银十 面试宝典 Spring、MyBatis、SpringMVC面试题 超级无敌全的面试题汇总(超万字的面试题,让你的SSM框架无可挑剔)
Spring、MyBatis、SpringMVC 框架 - 面试宝典 又到了 金三银四、金九银十 的时候了,是时候收藏一波面试题了,面试题可以不学,但不能没有!🥁🥁🥁 一个合格的 计算机打工人 ,收藏夹里…...
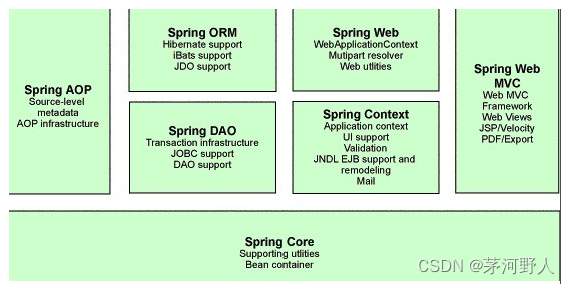
JAVA开发(Spring框架详解)
javaweb项目几乎已经离不开spring框架了,spring 是一个典型的分层架构框架,它包含一系列的功能并被分为多个功能模块,springboot对spring框架又做了一层封装,以至于很多人对原来的spring框架越来越不了解。 要谈Spring的历史&…...

自学大数据第八天~HDFS命令(二)
嗨喽,好久不见,最近抽空复习了一下hadoop,书读百遍,其意自现这句话还真是; 继续学习HDFS常用命令 改变文件 拥有者~chown hdfs dfs -chown -R hadoop /user/hadoop使用 -R 将使改变在目录结构下递归进行。命令的使用者必须是超级用户。 改变文件所属组-chgrp hdfs dfs -chgr…...
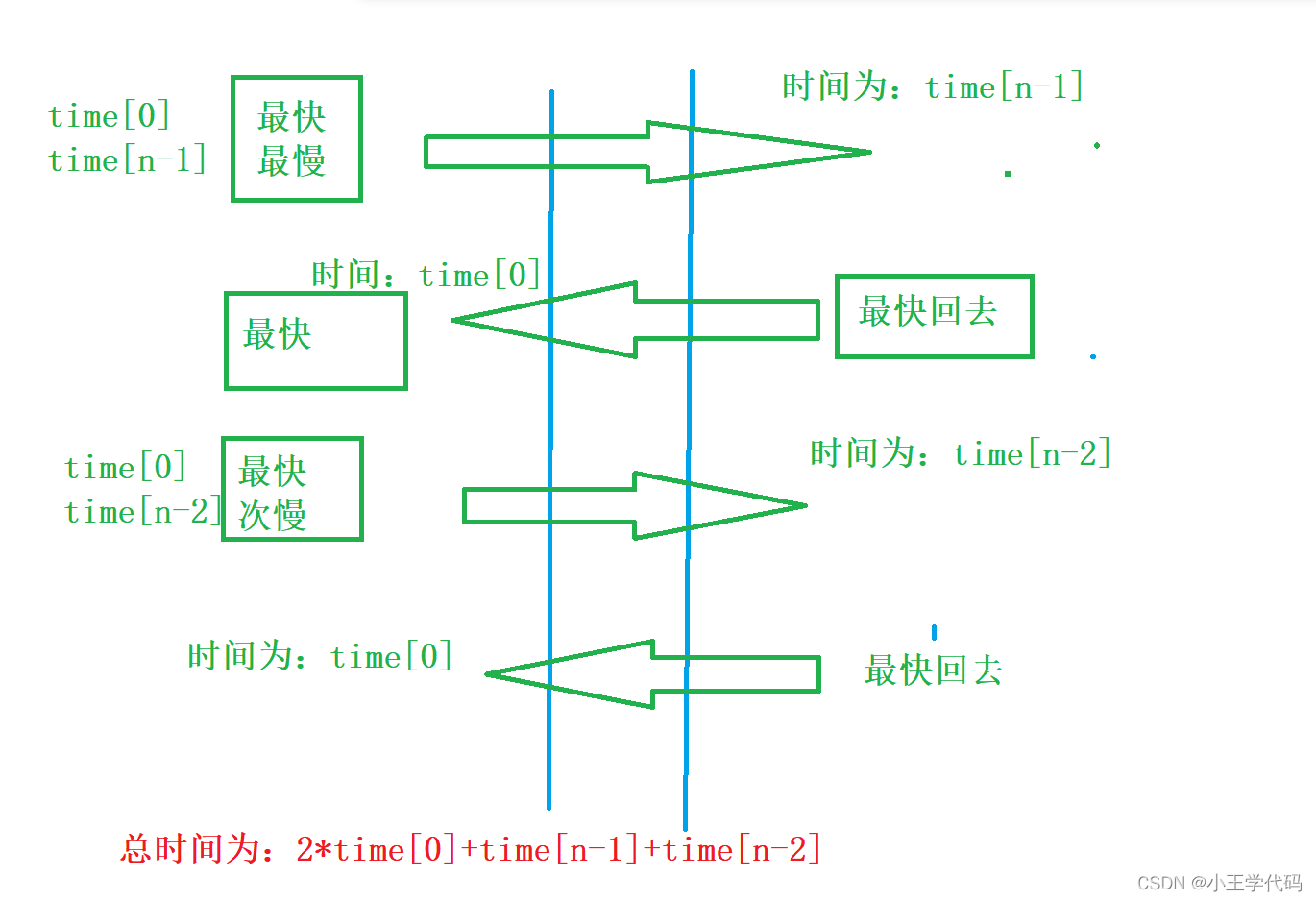
贪心算法(几种常规样例)
贪心算法(几种常规样例) 贪心算法,指在对问题进行求解的时候,总是做出当前看来是最好的选择。也就是说不从整体上最优上考虑,算法得到的结果是某种意义上的局部最优解 文章目录贪心算法(几种常规样例&…...

【数据结构】基础知识总结
系列综述: 💞目的:本系列是个人整理为了数据结构复习用的,由于牛客刷题发现数据结构方面和王道数据结构的题目非常像,甚至很多都是王道中的,所以将基础知识进行了整理,后续会将牛客刷题的错题一…...
宣布推出 .NET 社区工具包 8.1!
我们很高兴地宣布 .NET Community Toolkit 8.1 版正式发布!这个新版本包括呼声很高的新功能、bug 修复和对 MVVM 工具包源代码生成器的大量性能改进,使开发人员在使用它们时的用户体验比以往更好! 就像在我们之前的版本中一样,我…...

ChatGPT解开了我一直以来对自动化测试的疑惑
目录 前言 与ChatGPT的对话 什么是自动化测试,我该如何做到自动化测试,或者说需要借助什么工具可以做到自动化测试? 自动化测试如何确保数据的准确性 自动化测试是怎么去验证数据的 如何通过断言验证数据 自动化测试有哪些验证工具可以验证数据 总结 前言…...
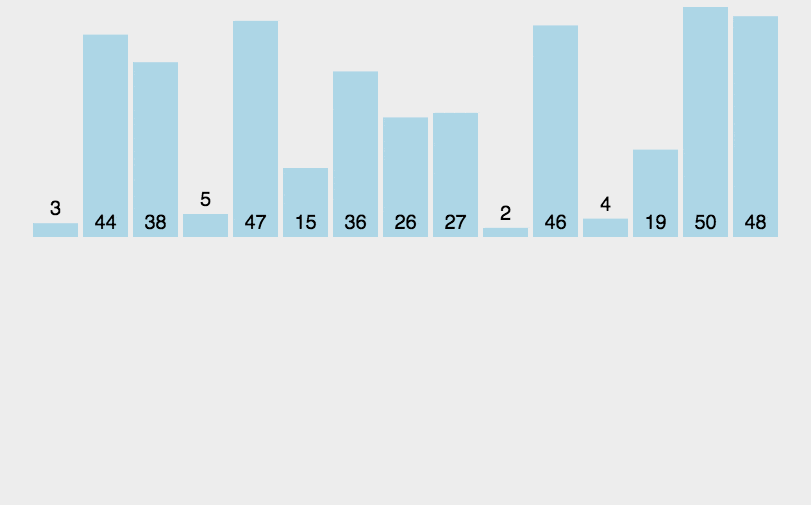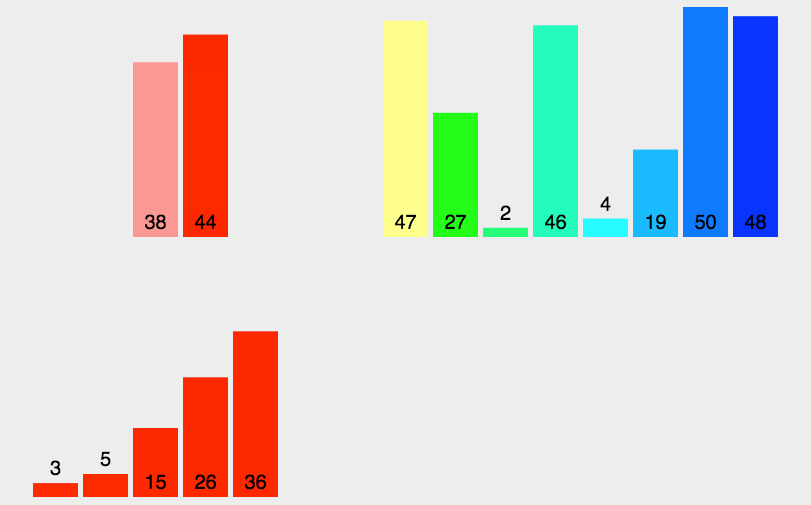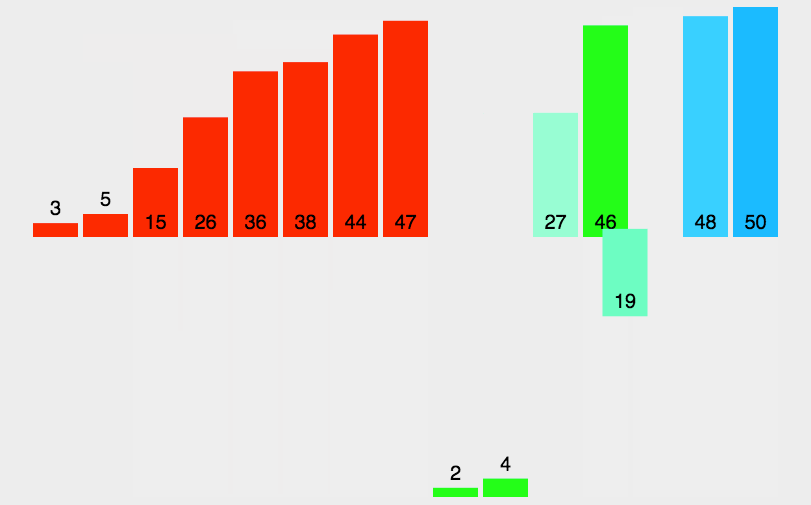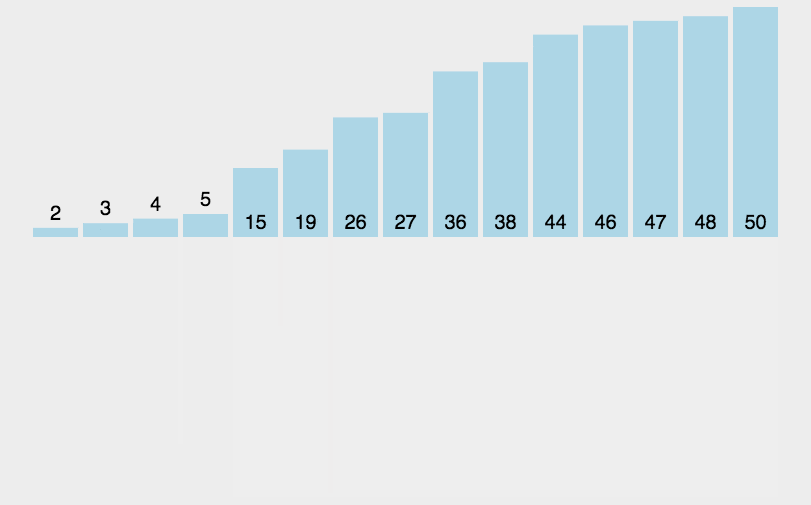
十大经典排序算法(上)
目录 1.1冒泡排序 1. 算法步骤 3.什么时候最快 4. 什么时候最慢 5.代码实现 1.2选择排序 1. 算法步骤 2. 动图演示 3.代码实现 1.3 插入排序 1. 算法步骤 2. 动图演示 3. 算法实现 1.4 希尔排序 1. 算法步骤 2. 动图演示 3.代码实现 1.5 归并排序 1. 算法步骤 2…...

如何从 MySQL 读取 100w 数据进行处理
文章目录 场景常规查询流式查询MyBatis 流式查询接口非流式查询和流式查询区别游标查询场景 大数据量操作的场景大致如下: 1、 数据迁移; 2、 数据导出; 3、 批量处理数据; 在实际工作中当指定查询数据过大时,我们一般使用分页查询的方式一页一页的将数据放到内存处理。…...
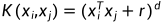
【数据降维-第2篇】核主成分分析(KPCA)快速理解,及MATLAB实现
一篇介绍了PCA算法的快速理解和应用,本章讲一下KPCA。KPCA方法与PCA方法一样,是有着扎实的理论基础的,相关理论在论文上以及网络上可以找到大量的材料,所以这篇文章还是聚焦在方法的快速理解以及应用上,此外还会对同学…...
Python+ChatGPT实战之进行游戏运营数据分析
文章目录一、数据二、目标三、解决方案1. DAU2. 用户等级分布3. 付费率4. 收入情况5. 付费用户的ARPU最近ChatGPT蛮火的,今天试着让ta写了一篇数据分析实战案例,大家来评价一下!一、数据 您的团队已经为您提供了一些游戏数据,包括…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...
