【Linux 线程】线程的基本概念、LWP的理解
文章目录
- 一、ps -L 指令🍎
- 二、线程控制
一、ps -L 指令🍎
- 🐧 使用
ps -L命令查看轻量级进程信息; - 🐧
pthread_self()用于获取用户态线程的tid,而并非轻量级进程ID; - 🐧
getpid()用于获取当前进程的id,而并非某个特定轻量级进程;
二、线程控制
🍎
Linux操作系统不会直接提供给我们线程的系统调用,只会提供轻量级进程的系统调用。
🍎 将轻量级进程的接口进行封装,给用户在应用层封装一个pthread线程库。
几个细节知识点:🔍
- 什么叫做主线程呢 ?🍎
主线程:通常指的是程序启动时最初创建并执行的线程,即从
main函数开始执行的线程。CPU 调度的基本单位是线程,PID == LWP的线程叫做 主线程。
- 简述什么是 LWP ?🍎
LWP:是轻量级进程,在Linux下进程是资源分配的基本单位,线程是CPU调度的基本单位,而线程使用进程pcb描述实现,并且同一个进程中的所有pcb共用 同一个虚拟地址空间,因此相较于传统进程更加轻量化。
- 请简述
LWP与pthread_create创建的线程之间的关系 ? 🍎
pthread_create是一个库函数,功能是在用户态创建一个用户线程,而这个线程的运行调度是基于一个 轻量级进程 实现的。
- 请简述轻量级进程ID与进程ID之间的区别 ?🍎
因为
Linux下的轻量级进程是一个pcb,每个轻量级进程都有一个自己的轻量级进程ID(pcb中的pid),而同一个程序中的轻量级进程组成线程组,拥有一个共同的线程组ID。
- 共享资源、临界区、临界资源的区别 ? 🍎
①🐧 共享资源:表示能被多个执行流同时访问的资源;
②🐧 临界区:对临界资源进行操作的代码段;
③🐧 临界资源:同一时间只能有一个执行流访问访问的共享资源;
- 对
mutex的理解 ?🍎
mutex简单理解就是一个0/1计数器,用于标记资源访问状态;
0表示已经有执行流加锁成功,资源处于不可访问;
1表示未加锁,资源可访问;
- 请简述什么是线程互斥,为什么需要互斥 ? 🍎
线程互斥指的是多个线程间对临界资源进行争夺访问时有可能会造成数据的二义性,因此通过保证同一时间只有一个线程能够访问临界资源的方式实现线程对临界资源的访问安全性。
pthread_create创建一个线程 🔍


相关文章:

【Linux 线程】线程的基本概念、LWP的理解
文章目录 一、ps -L 指令🍎二、线程控制 一、ps -L 指令🍎 🐧 使用 ps -L 命令查看轻量级进程信息;🐧 pthread_self() 用于获取用户态线程的 tid,而并非轻量级进程ID;🐧 getpid() 用…...
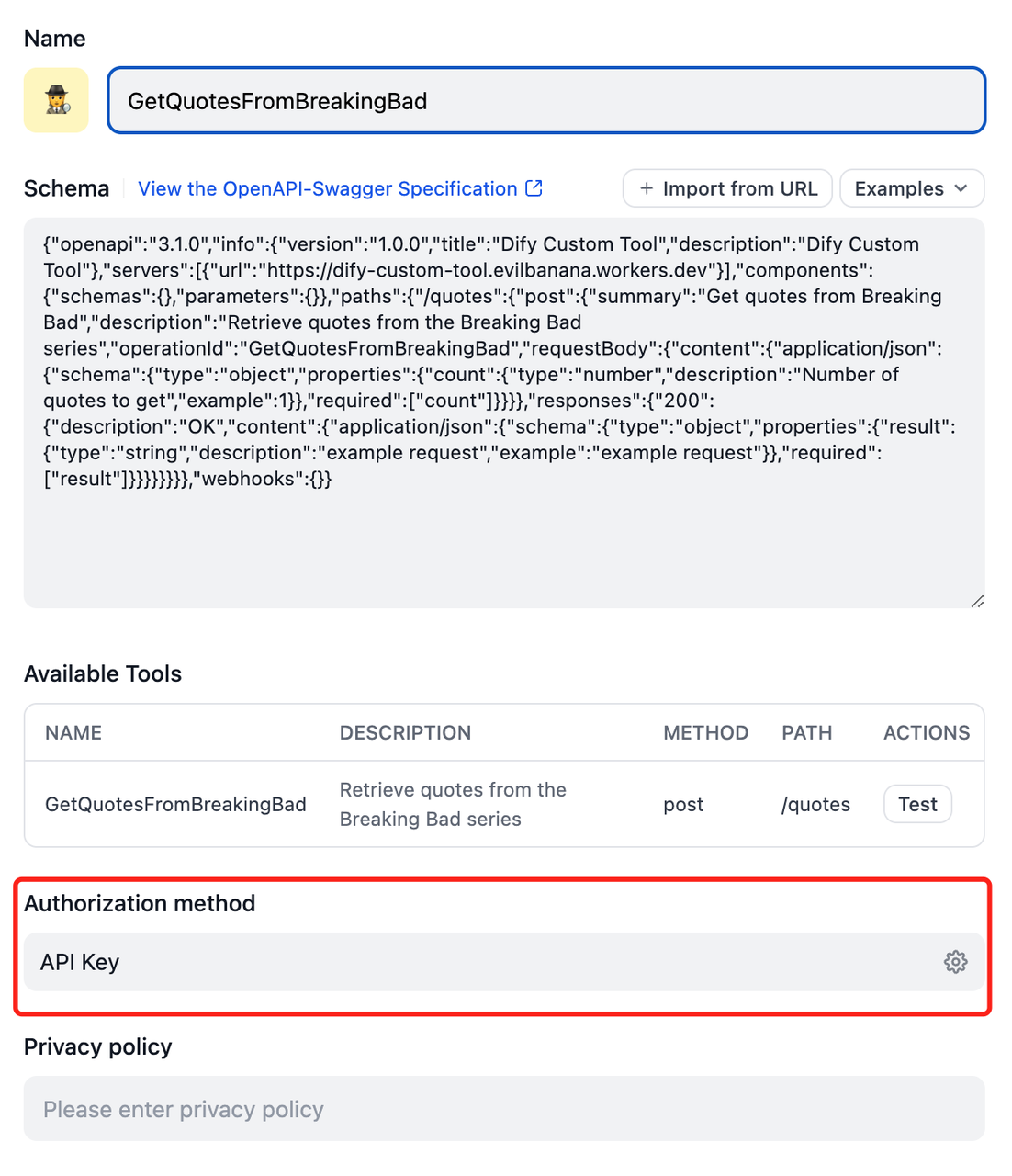
Dify中的工具
Dify中的工具分为内置工具(硬编码)和第三方工具(OpenAPI Swagger/ChatGPT Plugin)。工具可被Workflow(工作流)和Agent使用,当然Workflow也可被发布为工具,这样Workflow(工…...

在Visutal Studio 2022中完成D3D12初始化
在Visutal Studio 2022中完成DirectX设备初始化 1 DirectX121.1 DirectX 简介1.2 DirectX SDK安装2 D3D12初始化2.1 创建Windwos桌面项目2.2 修改符合模式2.3 下载d3dx12.h文件2.4 创建一个异常类D3DException,定义抛出异常实例的宏ThrowIfFailed3 D3D12的初始化步骤3.1 初始化…...

MobaXterm工具
MobaXterm 是一个增强型的 Windows 终端。其为 Windows 桌面提供所有重要的远程网络终端工具(如 SSH、X11、RDP、VNC、FTP、SFTP、Telnet、Serial、Mosh、WSL 等),和 Unix 命令(如 bash、ls、cat、sed、grep、awk、rsync 等&#…...

二分图练习
对于二分图我们可以用染色法 #include<bits/stdc.h> using namespace std;#define int long long const int N 2e65; int e[N],ne[N],h[N],idx 0; int colo[N]; int num 0;void add(int x,int y){e[idx] y;ne[idx] h[x];h[x] idx; } void dfs(int nod,int c){colo…...

创新设计策略:提升大屏幕可视化设计效果的关键方法
随着科技的不断发展和数据量的快速增长,数据可视化大屏在各个行业中的应用越来越广泛,可以帮助人们更好地理解和分析数据,可视化大屏设计也因此成了众多企业的需求。但很多设计师对可视化大屏设计并不了解,也不知道如何制作可视化…...

论文 | Chain-of-Thought Prompting Elicits Reasoningin Large Language Models 思维链
这篇论文研究了如何通过生成一系列中间推理步骤(即思维链)来显著提高大型语言模型进行复杂推理的能力。论文展示了一种简单的方法,称为思维链提示,通过在提示中提供几个思维链示例来自然地激发这种推理能力。 主要发现࿱…...

[机器学习]-人工智能对程序员的深远影响——案例分析
机器学习和人工智能对未来程序员的深远影响 目录 机器学习和人工智能对未来程序员的深远影响1. **自动化编码任务**1.1 代码生成1.2 自动调试1.3 测试自动化 2. **提升开发效率**2.1 智能建议2.2 项目管理 3. **改变编程范式**3.1 数据驱动开发 4. **职业发展的新机遇**4.1 AI工…...

AI学习环境 没有更好的替代 - (Google)Drive + Colab
在开始正题前,请容许我做一番回顾,并夹带一点点私货(谷歌扛旗的开源精神还没有死,并且会是未来的举足轻重的力量) 卧龙凤雏,一时瑜亮。一切的缘起应该是世纪初的门户网站乱战。 彼时,谷歌是从…...

【观成科技】Websocket协议代理隧道加密流量分析与检测
Websocket协议代理隧道加密流量简介 攻防场景下,Websocket协议常被用于代理隧道的搭建,攻击者企图通过Websocket协议来绕过网络限制,搭建一个低延迟、双向实时数据传输的隧道。当前,主流的支持Websocket通信代理的工具有…...

DangerWind-RPC-framework---三、服务端下机
当一台机器下线时,面临很多问题:如何将其从注册中心下线?如何清理释放资源?客户端拉取服务列表时也使用了本地缓存,如何及时更新本地缓存? 服务端机器的优雅下线需要使用ShutdownHook,这相当于添…...

基于Make的c工程No compilation commands found报错
由于安装gcc时只安装了build-essential,没有将其添加到环境变量中,因此打开Make工程时,CLion会产生如下错误: 要解决这个问题,一个方法是将GCC添加到环境变量中,但是这个方法需要修改至少两个配置文件&…...

c++:面向对象的继承特性
什么是继承 (1)继承是C源生支持的一种语法特性,是C面向对象的一种表现 (2)继承特性可以让派生类“瞬间”拥有基类的所有(当然还得考虑权限)属性和方法 (3)继承特性本质上是为了代码复用 (4)类在C编译器的内部可以理解为结构体,派…...

skywalking-2-客户端-php的安装与使用
skywalking的客户端支持php,真的很棒。 官方安装文档:https://skywalking.apache.org/docs/skywalking-php/next/en/setup/service-agent/php-agent/readme/ 前置准备 本次使用的php版本是8.2.13: php -v PHP 8.2.13 (cli) (built: Nov 21 2023 09:5…...

图文讲解IDEA如何导入JDBC驱动包
前言 学习JDBC编程,势必要学会如何导入驱动包,这里笔者用图文的方式来介绍 视频版本在这里 50秒教你怎么导入驱动包然后进行JDBC编程的学习_哔哩哔哩_bilibili 忘记录音频了,大伙凑合着看 下载驱动包 https://mvnrepository.com/artifact/mysql/mysql-connector-java 去中…...
java.lang.NullPointerException: null cannot be cast to non-null type kotlin.Int
java.lang.NullPointerException: null cannot be cast to non-null type kotlin.Int fun main(args: Array<String>) {var any1: Any?any1 nullval n1 any1 as? Int ?: -2024println(n1)kotlin.runCatching {var any2: Any?any2 nullval n2 any2 as Intprintln(…...

scrapy写爬虫
Scrapy是一个用于爬取网站数据并提取结构化信息的Python框架 一、Scrapy介绍 1.引擎(Engine) – Scrapy的引擎是控制数据流和触发事件的核心。它管理着Spider发送的请求和接收的响应,以及处理Spider生成的Item。引擎是Scrapy运行的驱动力。…...

Mybatis study
一、Mybatis Plus mybatis-plus指定实体类字段不查询 加标签 TableField(exist false) Spring Data Jpa学习 干我们这行,啥时候懈怠,就意味着长进的停止,长进的停止就意味着被淘汰,只能往前冲,直到凤凰涅槃的一天&am…...

【论文速读】《面向深度学习的联合消息传递与自编码器》
这篇文章来自华为的渥太华无线先进系统能力中心和无线技术实验室,作者中有大名鼎鼎的童文。 一、自编码架构的全局收发机面临的主要问题 文章对我比较有启发的地方,是提到自编码架构的全局收发机面临的主要问题: 问题一:基于随…...

防御---001
一、实验拓扑二、要求 1,DMZ区内的服务器,办公区仅能在办公时间内(9:00 - 18:00)可以访问,生产区的的设备全天可以访问. 2,生产区不允许访问互联网,办公区和游客区允许访问互联网 3,办公区设备10.0.2.10不允许访问DMZ…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

