力扣 hot100 -- 动态规划(下)
目录
💻最长递增子序列
AC 动态规划
AC 动态规划(贪心) + 二分
🏠乘积最大子数组
AC 动规
AC 用 0 分割
🐬分割等和子集
AC 二维DP
AC 一维DP
⚾最长有效括号
AC 栈 + 哨兵
💻最长递增子序列
300. 最长递增子序列 - 力扣(LeetCode)
子序列:不用连续
子串:要求连续
AC 动态规划
时间 O(n^2)
/*
dp[i] : 第 i 个元素结尾的最长子序列长度(下标0开始)
dp[i] = max(dp[i], dp[j] + 1)
初始化 : dp[i] = 1
*/
class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();vector<int> dp(n + 1, 1);for (int i = 1; i < n; ++i)for (int j = 0; j < i; ++j) if (nums[j] < nums[i])dp[i] = max(dp[i], dp[j] + 1);int ans = 1;for (auto x : dp)ans = max(ans, x);return ans;}
};AC 动态规划(贪心) + 二分
二分实现 O(logn) 查找,为了使用二分,我们需要让 dp[] 数组有序,所以需要改变 dp[] 数组的含义(状态)
贪心策略:tails 中存储的元素越小,上升的子序列越长
举例解释
nums[] = {7, 8, 9, 1, 2, 3, 4, 5};
遍历完 7 8 9 后 tails[] = {7, 8, 9};
接着遍历到 1,那么二分查找 tails[],找到第一个比 tails 大的位置,即 7,替换后变成
tails[] = {1, 8, 9};
如果没有比当前 nums[] 值大的元素,直接加到后面
最后输出 tails[] 长度,就是最长上升子序列长度
时间 O(nlogn)
/*
tails[i] : 长度 i+1 子序列的尾部元素
1)nums[] 中当前元素 x > tails.back(), x 插入 tails 最后
2)否则, 二分查找 tails[] 中第一个 > x 的元素, 替换成 x
最后返回 tails[] 大小
*/
class Solution {
public:int lengthOfLIS(vector<int>& nums) {vector<int> tails;tails.push_back(nums[0]);for (auto x : nums) {if (x > tails.back()) {tails.push_back(x);continue;}int l = 0, r = tails.size() - 1;while (l < r) {int mid = (l + r) >> 1;if (tails[mid] < x)l = mid + 1;elser = mid;}tails[l] = x;}return tails.size();}
};
// 检验二分边界
// tails[]: 1 3 5 -- x: 3/4
// tails[]: 1 3 5 7 -- x: 3/4/5🏠乘积最大子数组
152. 乘积最大子数组 - 力扣(LeetCode)
注意是“连续子数组”
AC 动规
1)滚动
本题,dp[i] 都是基于 dp[i -1] 得到的,所以可以将一维数组变成一个变量,即 “滚动数组”
2)坑
遍历数组,更新 3 个 dp 变量时,maxDp 基于上一个 maxDp 没问题
但是 maxDp 更新后,minDp 还是基于上一个 maxDp
所以需要一个临时变量保存上一个 maxDp
然后 dp 可以直接基于新的 maxDp
3)坑2
题目保证 32 位,也就是 10^9,但是,样例里有一组 10^19 次方的....
所以,有 4 个地方要加 double,防止类型不匹配 或 heap flow(堆溢出)
时间 O(n)
/*
滚动数组,一维数组变变量
maxDp[i] : 第 i 个元素结尾的最大值
minDp[i] : 第 i 个元素结尾的最小值
dp[i] : 只选前 i 的元素的最大值
*/
class Solution {
public:int maxProduct(vector<int>& nums) {int n = nums.size();if (n == 1)return nums[0];double maxDp = nums[0], minDp = nums[0], dp = nums[0];for (int i = 1; i < n; ++i) {double t = maxDp; // 临时变量maxDp = max(max((double)nums[i], maxDp*nums[i]), minDp*nums[i]);minDp = min(min((double)nums[i], t*nums[i]), minDp*nums[i]);dp = max(dp, maxDp); // 上一个 dp 和 新的 maxDp 取较大值}return (double)dp;}
};AC 用 0 分割
用 0 分割成多个连续的子数组,对每个子数组:
1)偶数个负数,直接相乘(负数数量 0, 2, 4, 6...)
2)奇数个负数:
a. 左到右相乘,直到最后一个负数之前
b. 右到左,直到最后一个负数之前
取 a. b. 的 max()
3)实际遍历中,先左到右遍历,后右到左遍历,单次遍历中,只需要动态更新最大值(包含了偶数,奇数个负数的两种情况)
时间 O(n)
class Solution {
public:int maxProduct(vector<int>& nums) {double ans = nums[0];double t = 1; // 临时变量保存乘积// 左到右for (int i = 0; i < nums.size(); ++i) {t *= nums[i];ans = max(ans, t);if (t == 0)t = 1; // 用 0 分割子数组}// 右到左t = 1;for (int i = nums.size() - 1; i >= 0; --i) {t *= nums[i];ans = max(ans, t);if (t == 0)t = 1;}return (int)ans;}
};🐬分割等和子集
416. 分割等和子集 - 力扣(LeetCode)
AC 二维DP
01背包画表格类似这样
坑:
和为奇数,直接返回 false,否则打表会发现,出现了一些奇怪的错误
含义:
dp[i][j] : 只从 [0, i] 区间里选,每个数最多选 1 次,和为 j
递推式:
选第 i 个:dp[i - 1][j - nums[i]]
不选第 i 个:dp[i - 1][j]
第 i 个数 == 总和的一半
dp[i][j] = dp[i - 1][j - nums[i]] || dp[i - 1][j] || (nums[i] == sum/2)
初始化:
根据递推式,只需初始化第 0 行,即只从 [0, 0] 区间选,和为 nums[0] 的 == 1,其他为 0
输出:
dp[n - 1][sum / 2]:表示从 [0, n - 1] 选, 和为总和一半, 即等和子集
O(n * sum/2)
// dp[i][j] = dp[i - 1][j - nums[i]] || dp[i - 1][j] || (nums[i] == sum/2)
// 输出 dp[n - 1][sum / 2]
class Solution {
public:bool canPartition(vector<int>& nums) {int sum = 0, n = nums.size();for (auto x : nums)sum += x;if (sum % 2 == 1)return false; // 和为奇数// n 行, 每一行就是 vector<int>(), 这一行表示总和 0 ~ sum/2, 初始化为 0vector<vector<int>> dp(n, vector<int>(sum / 2 + 1, 0));if (nums[0] <= sum/2)dp[0][nums[0]] = 1; // 从 [0, 0] 选, 和为nums[0]for (int i = 1; i < n; ++i)for (int j = 0; j <= sum/2; ++j) {dp[i][j] = dp[i - 1][j] || (nums[i] == sum/2);if (j >= nums[i]) // 防止越界dp[i][j] = dp[i][j] || dp[i - 1][j - nums[i]];}return dp[n - 1][sum / 2];}
};
AC 一维DP
考虑到递推式 dp[i][j] 都是来源于 dp[i - 1][...],可以将二维变成一维,优化空间👇
那么为什么要逆序遍历子集的和 j 呢,因为,dp[j] 都是基于上一行的,旧的(未被修改的) dp[j] 和 dp[j - nums[i]]
如果顺序遍历,dp[j - nums[i]] 会被多次修改,也就是取了多个元素,而题目规定只能取一个
顺序遍历适合完全背包,而不是 01 背包

// dp[j] :和为 j
// dp[j] = dp[j - nums[i]] || dp[j] || (nums[i] == sum/2)
// 输出 dp[sum / 2]
class Solution {
public:bool canPartition(vector<int>& nums) {int sum = 0, n = nums.size();for (auto x : nums)sum += x;if (sum % 2 == 1)return false; // 和为奇数// 和的一半 +1 个元素vector<int> dp(sum / 2 + 1, 0);if (nums[0] <= sum/2)dp[nums[0]] = 1; // 从 [0, 0] 选, 和为nums[0]for (int i = 1; i < n; ++i)for (int j = sum/2; j >= 0; --j) {dp[j] = dp[j] || (nums[i] == sum/2);if (j >= nums[i]) // 防止越界dp[j] = dp[j] || dp[j - nums[i]];}return dp[sum / 2];}
};
⚾最长有效括号
32. 最长有效括号 - 力扣(LeetCode)
AC 栈 + 哨兵
求连续的最长有效括号
如果不连续,栈就会被清空最后一个元素,再插入新的下标,即更新了栈顶的元素
初始插入 -1(哨兵),防止先遇到右括号,栈为空就 pop 导致的栈溢出
时间 O(n)
class Solution {
public:int longestValidParentheses(string s) {int ans = 0;if (s.size() == 0) return 0;stack<int> st;st.push(-1); // 防止溢出, 为后面的连续准备for (int i = 0; i < s.size(); ++i) {if (s[i] == '(') // 左括号st.push(i); else { // 右括号st.pop();if (st.empty())st.push(i);else ans = max(ans, i - st.top()); // 连续的长度}}return ans;}
};相关文章:

力扣 hot100 -- 动态规划(下)
目录 💻最长递增子序列 AC 动态规划 AC 动态规划(贪心) 二分 🏠乘积最大子数组 AC 动规 AC 用 0 分割 🐬分割等和子集 AC 二维DP AC 一维DP ⚾最长有效括号 AC 栈 哨兵 💻最长递增子序列 300. 最长递增子序列…...
【计算机毕业设计】018基于weixin小程序实习记录
🙊作者简介:拥有多年开发工作经验,分享技术代码帮助学生学习,独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。🌹赠送计算机毕业设计600个选题excel文件,帮助大学选题。赠送开题报告模板ÿ…...

力扣之有序链表去重
删除链表中的重复元素,重复元素保留一个 p1 p2 1 -> 1 -> 2 -> 3 -> 3 -> null p1.val p2.val 那么删除 p2,注意 p1 此时保持不变 p1 p2 1 -> 2 -> 3 -> 3 -> null p1.val ! p2.val 那么 p1,p2 向后移动 p1 …...

Apache配置与应用(优化apache)
Apache配置解析(配置优化) Apache链接保持 KeepAlive:决定是否打开连接保持功能,后面接 OFF 表示关闭,接 ON 表示打开 KeepAliveTimeout:表示一次连接多次请求之间的最大间隔时间,即两次请求之间…...
怎么将3张照片合并成一张?这几种拼接方法很实用!
怎么将3张照片合并成一张?在我们丰富多彩的日常生活里,是否总爱捕捉那些稍纵即逝的美好瞬间,将它们定格为一张张珍贵的图片?然而,随着时间的推移,这些满载回忆的宝藏却可能逐渐演变成一项管理挑战ÿ…...
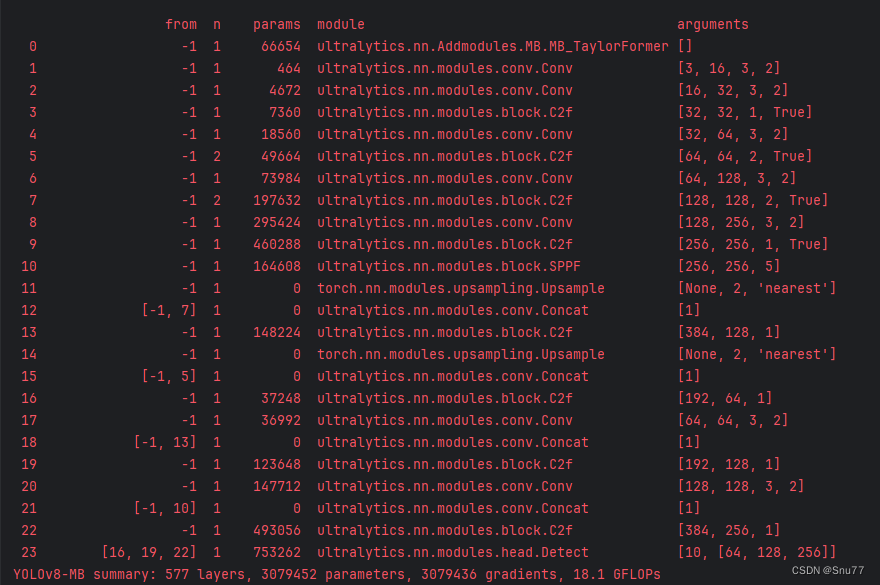
YOLOv10改进 | 图像去雾 | MB-TaylorFormer改善YOLOv10高分辨率和图像去雾检测(ICCV,全网独家首发)
一、本文介绍 本文给大家带来的改进机制是图像去雾MB-TaylorFormer,其发布于2023年的国际计算机视觉会议(ICCV)上,可以算是一遍比较权威的图像去雾网络, MB-TaylorFormer是一种为图像去雾设计的多分支高效Transformer…...
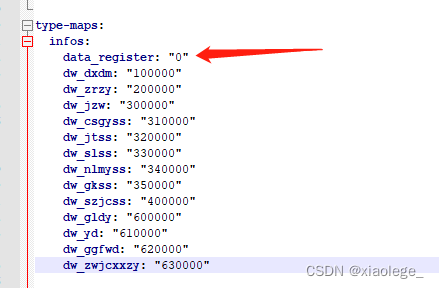
spring boot读取yml配置注意点记录
问题1:yml中配置的值加载到代码后值变了。 现场yml配置如下: type-maps:infos:data_register: 0ns_xzdy: 010000ns_zldy: 020000ns_yl: 030000ns_jzjz: 040000ns_ggglyggfwjz: 050000ns_syffyjz: 060000ns_gyjz: 070000ns_ccywljz: 080000ns_qtjz: 090…...

电子电气架构 --- 关于DoIP的一些闲思 下
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的人和事,多看一眼都是你的不对。非必要不费力证明自己,无利益不试图说服别人,是精神上的节…...

Java getSuperclass和getGenericSuperclass
1.官方API对这两个方法的介绍 getSuperclass : 返回表示此 Class 所表示的实体(类、接口、基本类型或 void)的超类的 Class。如果此 Class 表示 Object 类、一个接口、一个基本类型或 void,则返回 null。如果此对象表示一个数组类ÿ…...

ARM功耗管理标准接口之ACPI
安全之安全(security)博客目录导读 思考:功耗管理有哪些标准接口?ACPI&PSCI&SCMI? Advanced Configuration and Power Interface Power State Coordination Interface System Control and Management Interface ACPI可以被理解为一…...

2024年网络监控软件排名|10大网络监控软件是哪些
网络安全,小到关系到企业的生死存亡,大到关系到国家的生死存亡。 因此网络安全刻不容缓,在这里推荐网络监控软件。 2024年这10款软件火爆监控市场。 1.安企神软件: 7天免费试用https://work.weixin.qq.com/ca/cawcde06a33907e6…...

通过Arcgis从逐月平均气温数据中提取并计算年平均气温
通过Arcgis快速将逐月平均气温数据生成年平均气温数据。本次用2020年逐月平均气温数据操作说明。 一、准备工作 (1)准备Arcmap桌面软件; (2)准备2020年逐月平均气温数据(NC格式)、范围图层数据&…...

每日一题~abc356(对于一串连续数字 找规律,开数值桶算贡献)
添加链接描述 题意:对于给定的n,m 。计算0~n 每一个数和m & 之后,得到的数 的二进制中 1的个数的和。 一位一位的算。最多是60位。 我们只需要计算 在 1-n这些数上,有多少个数 第i位 为1. 因为是连续的自然数,每一位上1 的…...

商业合作方案撰写指南:让你的提案脱颖而出的秘诀
作为一名策划人,撰写一份商业合作方案需要细致的规划和清晰的表达。 它是一个综合性的过程,需要策划人具备市场洞察力、分析能力和创意思维。 以下是能够帮助你撰写一份有效的商业合作方案的关键步骤和要点: 明确合作目标:设定…...

【MySQL】锁(黑马课程)
【MySQL】锁 0. 锁的考察点1. 概述1. 锁的分类1.1 属性分类1.2 粒度分类 2. 全局锁2.1 全局锁操作2.2.1 备份问题 3. 表级锁3.1 表锁3.2 语法3.3 表共享读锁(读锁)3.4 表独占写锁(写锁)3.5 元数据锁(meta data lock, MDL)3.6 意向…...
1.10编程基础之简单排序--02:奇数单增序列
OpenJudge - 02:奇数单增序列http://noi.openjudge.cn/ch0110/02/ 描述 给定一个长度为N(不大于500)的正整数序列,请将其中的所有奇数取出,并按升序输出。 输入 共2行: 第1行为 N; 第2行为 N 个正整数,其间用空格间隔。 输出 增序输出的奇数序列,数据之间以逗号间隔。数…...

【leetcode78-81贪心算法、技巧96-100】
贪心算法【78-81】 121.买卖股票的最佳时机 class Solution:def maxProfit(self, prices: List[int]) -> int:dp[[0,0] for _ in range(len(prices))] #dp[i][0]第i天持有股票,dp[i][1]第i天不持有股票dp[0][0] -prices[0]for i in range(1, len(prices)):dp[…...

IEC62056标准体系简介-4.IEC62056-53 COSEM应用层
为在通信介质中传输COSEM对象模型,IEC62056参照OSI参考模型,制定了简化的三层通信模型,包括应用层、数据链路层(或中间协议层)和物理层,如图6所示。COSEM应用层完成对COSEM对象的属性和方法的访问ÿ…...

嵌入式应用开发之代码整洁之道
前言:本系列教程旨在如何将自己的代码写的整洁,同时也希望小伙伴们懂如何把代码写脏,以备不时之需,同时本系列参考 正点原子 , C代码整洁之道,编写可读的代码艺术。 #好的代码的特点 好的代码应该都有着几…...

iwconfig iwpriv学习之路
iwconfig和iwpriv是两个常用的wifi调试工具,最近需要使用这两个工具完成某款wifi芯片的定频测试,俗话说好记性不如烂笔头,于是再此记录下iwconfig和iwpriv的使用方式。 -----再牛逼的梦想,也抵不住傻逼般的坚持! ----2…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

