022-GeoGebra中级篇-几何对象之直线与坐标轴
本文主要介绍一下GeoGebra中直线的常见输入方式,比如工具栏输入、表达式输入、函数输入,最后再把坐标轴的调用简单介绍一下。内容比起传统的教学更偏向于实战一些,若感兴趣欢迎继续阅读。
目录
- 一、直线
- 1. 关于工具栏绘制
- (1)常用直线—lines集
- (2)常用直线—Contsruct集
- 2. 关于表达式的绘制
- (1)解析式方式
- (2)过两点建立
- 二、坐标轴
- 三、文章最后
一、直线
1. 关于工具栏绘制
有时候为了图快,我通常是采用工具栏输入与表达式输入相互结合的方式,比如过一点绘制一条垂线,我就直接用工具栏的垂线工具一拖就好了,当然,还需要返回到表达式栏看一下,比如修改下线的标签之类。
(1)常用直线—lines集
线段的创建非常简单,建议在表达式栏输入自己的两个点,然后在工具栏用线段工具一连就好了。


(2)常用直线—Contsruct集

这几种直线分别用来“过一点做直线的垂线”、“求线段的中垂线”、“过一点做线段的平行线”、“画角的角平分线”、“绘制圆的切线”,如果已经有点了,建议直接在这里用工具绘制就可以了,方便快捷。
2. 关于表达式的绘制
(1)解析式方式
g:3x+4y=2

解析式的方式记得前面写一个标签,然后跟上一个英文的冒号。
(2)过两点建立
“g:X=(-5,5)+t(4,-3)

这种属于解析式的变形,在数学中是不允许出现的,但是在GeoGebra中是可以出现的,输入后会根据这两个点直接计算出解析式。
二、坐标轴
坐标轴需注意的是被调用,两个坐标轴可以通过“xAxis”和“yAxis”指令被调用。
比如过(2,2)点做X轴的垂线,绘图后看一下表达式栏,可以发现是这样的:
f: PerpendicularLine(A,xAxis)
在这里xAxis就已经被调用了。

三、文章最后
若有任何问题都可以在这个铺子问客服,也会有资源相送,GeoGebra、PPT、平面动画、3D动画等各种技术都可以,祝好!

相关文章:

022-GeoGebra中级篇-几何对象之直线与坐标轴
本文主要介绍一下GeoGebra中直线的常见输入方式,比如工具栏输入、表达式输入、函数输入,最后再把坐标轴的调用简单介绍一下。内容比起传统的教学更偏向于实战一些,若感兴趣欢迎继续阅读。 目录 一、直线1. 关于工具栏绘制(1&#…...

node js安装、配置(Windows版)
目录 node js 安装 node js 全局配置 1、全局安装路径 2、全局缓存路径 3、修改环境变量 pnpm安装、卸载 全局安装pnpm 验证pnpm版本 卸载pnpm 1、移除全局安装的包 2、移除pnpm cli 脚本直接安装 npm安装的使用命令直接卸载 node js 安装 cmd 查看是否存在&…...
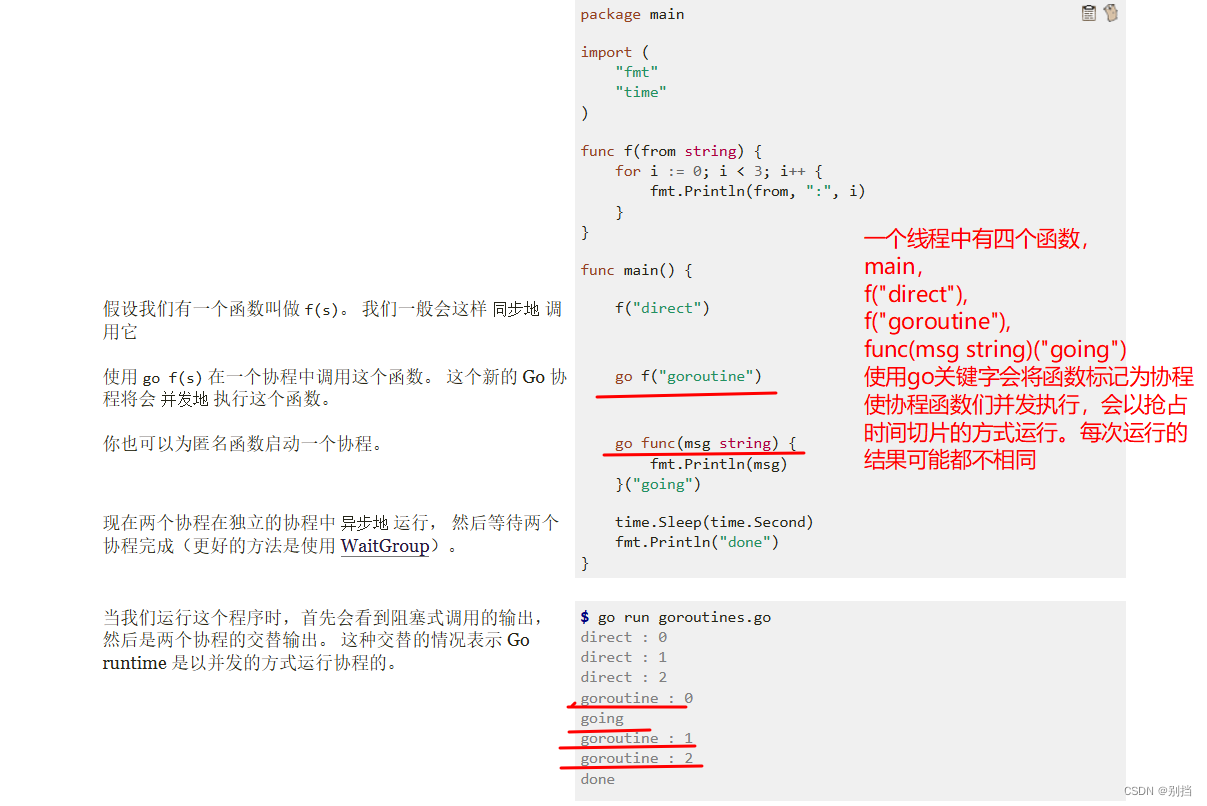
go语言day08 泛型 自定义错误处理 go关键字:协程
泛型: 抛错误异常 实现error接口类型 用java语言解释的话,实现类需要重写error类型的抽象方法Error().这样就可以自定义异常处理。 回到go语言,在Error()方法中用*argError 这样一个指针类来充当error接口的实现类。 在f2()方法中定义返回值…...

MySql性能调优01-[数据结构和索引]
数据结构和索引 什么是索引索引的种类常见索引数据结构和区别二叉树 红黑树 什么是索引 索引的种类 在Mysql中索引是在存储引擎层实现的,而不是在服务层实现的 按数据结构分:Btree索引、Hash索引、Full-text索引按存储结构分:聚簇索引、非聚…...

【算法入门-栈】逆波兰表达式求值
📖逆波兰表达式求值 ✅描述✅扩展:什么是逆波兰表达式✅题解方法一:栈✅题解方法二(数组模拟栈) 今天又刷了一道题,奥利给 刷题地址: 点击跳转 ✅描述 给定一个逆波兰表达式,求表达…...

【史上最全面ESP32教程】http通信
文章目录 前言HTTP协议是什么?HTTP协议的特点HTTP协议的常见应用 esp32 使用http通信通信流程基础使用HTTPClient 常用的函数函数介绍:void end(void);bool connected(void);void setReuse(bool reuse);void setUserAgent(const String& userAgent);…...
第二十七天 | 56. 合并区间、738. 单调递增的数字、968. 监控二叉树)
*算法训练(leetcode)第二十七天 | 56. 合并区间、738. 单调递增的数字、968. 监控二叉树
刷题记录 56. 合并区间*738. 单调递增的数字*968. 监控二叉树 56. 合并区间 leetcode题目地址 排序后遇到有重合的区间选择最大的区间保存即可,结果集中保存的是离当前区间最近的区间,因此使用当前区间与结果集中的最后一个集合比较查看是否有重合&…...

OpenJudge 奇数求和
目录 描述思路样例输入样例输出CodeCC 总时间限制: 1000ms 内存限制: 65536kB 描述 计算非负整数 m 到 n(包括m 和 n )之间的所有奇数的和,其中,m 不大于 n,且n 不大于300。例如 m3, n12, 其和则为:357911…...

【排序 - 快速排序】
快速排序(Quick Sort)是一种高效的排序算法,它基于分治(Divide and Conquer)的策略。这种排序算法的核心思想是选择一个基准元素,将数组分割成两部分,使得左边的元素都小于等于基准元素…...

pytest使用报错(以及解决pytest所谓的“抑制print输出”)
1. 测试类的类名问题 #codingutf-8import pytestclass TestClass1:def setup(self) -> None:print(setup)def test_01(self) -> None:print(test_01111111111111111111111)def test_02(self) -> None:print(test_02)以上述代码为例,如果类名是Test开头&am…...

开源项目编译harbor arm架构的包 —— 筑梦之路
GitHub - amy5200/harbor-arm64 先做个记录,空了再验证...

[笔记] SKF Enveloping FAQ 用户指南
文档编号:Application Note CM3013 1.名词解释: 1.1cavitationWhat Is Cavitation? | Pumps & Systems 叶片在液体中扰动形成的超声波 1.2 stiff machinehttps://suspensionlist.com/the-pros-and-cons-of-stiff-vs-soft-suspension-systems/ …...
 Part.3)
宪法学学习笔记(个人向) Part.3
宪法学学习笔记(个人向) Part 3 3. 国家基本制度 3.1 国家性质 3.1.1 国家性质概述 国家性质的概念 国家性质也称国体,或国家的阶级本质,是指各个阶级在国家中的地位(哪个阶层是统治阶层,哪个阶层是被统治阶层,哪个…...

联想拯救者Y7000 IRX9 笔记本接口功能介绍
适用机型:Legion Y7000 IRX9; 83JJ; USB(3.2 Gen 1)Type-接口摄像头开关组合音频插孔 多用于USB Type-C接口 以太网接口 多用途USB Type-C接口(支持USB Power Delivery)HDMI接口USB(3.2 Gen 1&…...

【ESP32】打造全网最强esp-idf基础教程——16.SmartConfig一键配网
SmartConfig一键配网 一、SmartConfig知识扫盲 在讲STA课程的时候,我们用的是代码里面固定的SSID和密码去连接热点,但实际应用中不可能这么弄,我们得有办法把家里的WiFi SSID和密码输入到设备里面去,对于带屏带输入设备还…...

MD5加密和注册页面的编写
MD5加密 1.导入包 npm install --save ts-md5 2.使用方式 import { Md5 } from ts-md5; //md5加密后的密码 const md5PwdMd5.hashStr("123456").toUpperCase(); 遇见的问题及用到的技术 注册页面 register.vue代码 <template><div class"wappe…...
【Android组件】封装加载弹框
📖封装加载弹框 ✅1. 构造LoadingDialog✅2. 调用LoadingDialog 效果: ✅1. 构造LoadingDialog 构造LoadingDialog类涉及到设计模式中的建造者模式,进行链式调用,注重的是构建的过程,设置需要的属性。 步骤一&#x…...

Spring源码二十:Bean实例化流程三
上一篇Spring源码十九:Bean实例化流程二中,我们主要讨论了单例Bean创建对象的主要方法getSingleton了解到了他的核心流程无非是:通过一个简单工厂的getObject方法来实例化bean,当然spring在实例化前后提供了扩展如:bef…...

前端导出文件时,后端代码出错如何将错误信息返回给前端展示
功能说明:前端导出excel时,后端出现异常,比如sql异常,或者创建excel时出现的异常,希望将这些异常信息返回给前端查看。 框架:vue3 axios Springboot 实现难度分析:前端导出excel,…...

解决Spring Boot应用中的内存优化问题
解决Spring Boot应用中的内存优化问题 大家好,我是微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 1. Spring Boot应用的内存管理 在开发和部署Spring Boot应用时,有效地管理内存是确保应用性能和稳…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...
