力扣1472.设计浏览器历史记录
力扣1472.设计浏览器历史记录
-
用双指针记录历史记录
- 以及栈顶高度
- 移动时会直接把之前的记录消掉
-
class BrowserHistory {int pos=-1;int top=0;string history[5010];public:BrowserHistory(string homepage) {visit(homepage);}void visit(string url) {pos ++;top = pos;history[top] = url;}string back(int steps) {if(steps >pos)steps = pos;pos -= steps;return history[pos];}string forward(int steps) {steps = min(steps,top - pos);pos += steps;return history[pos];}};
相关文章:

力扣1472.设计浏览器历史记录
力扣1472.设计浏览器历史记录 用双指针记录历史记录 以及栈顶高度移动时会直接把之前的记录消掉 class BrowserHistory {int pos-1;int top0;string history[5010];public:BrowserHistory(string homepage) {visit(homepage);}void visit(string url) {pos ;top pos;histor…...

准大一新生开学千万要带证件照用途大揭秘
1、提前关注好都有哪些考场,以及这些考场大致在网页的哪个位置。比如我选对外经贸大学,我就直接找到第二个点进去。 2、电脑上同时开了谷歌浏览器和IE浏览器,以及手机也登陆了。亲测下来,同一时间刷新,谷歌浏览器能显示…...

QImage显示图片像素
在Qt中,QImage 类是用来表示和处理图像的。如果你想查看或显示一个图片的像素数据,你可以使用 QImage 提供的方法来访问这些数据。以下是一些基本的方法来获取和显示图片的像素信息: 获取图像的像素格式: 使用 QImage::format() …...
uniapp使用高德地图(公众号+h5)
选择微信小程序的话后果就是你的地图出不来,出来了就报key异常 下面直接放配置和代码: 打包后的高德uni-app,uniCloud,serverless,高德地图,申请高德地图Key,配置使用高德地图,参数说明,高德开放平台用户名,百度地图,申请百度地图Key,配置使用百度地图,…...

深度学习与浅层学习:技术变革下的竞争态势
深度学习与浅层学习:技术变革下的竞争态势 在过去十年中,深度学习的崛起对整个人工智能领域产生了巨大影响,几乎在各种任务中显示出超越传统浅层学习方法的性能。这种变化不仅推动了技术的进步,还对硬件市场,尤其是显…...

LeetCode 219. 存在重复元素 II
LeetCode 219. 存在重复元素 II 给你一个整数数组 nums 和一个整数 k ,判断数组中是否存在两个 不同的索引 i 和 j ,满足 nums[i] nums[j] 且 abs(i - j) < k 。如果存在,返回 true ;否则,返回 false 。 示例 1&am…...

【目标检测】使用自己的数据集训练并预测yolov8模型
1、下载yolov8的官方代码 地址: GitHub - ultralytics/ultralytics: NEW - YOLOv8 🚀 in PyTorch > ONNX > OpenVINO > CoreML > TFLite 2、下载目标检测的训练权重 yolov8n.pt 将 yolov8n.pt 放在ultralytics文件夹下 3、数据集分布 注…...
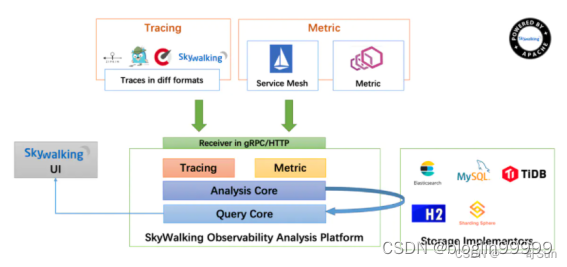
应用监控SkyWalking调研
参考: 链路追踪( Skyworking )_skywalking-CSDN博客 企业级监控项目Skywalking详细介绍,来看看呀-CSDN博客 SkyWalking 极简入门 | Apache SkyWalking 使用 SkyWalking 监控 ClickHouse Server | Apache SkyWalking https://zhuanlan.zhihu.com/p/3…...

Selenium使用注意事项:
find_element 和 find_elements 的区别 WebDriver和WebElement的区别 问题: 会遇到报错: selenium.common.exceptions.NoSuchElementException: Message: no such element: Unable to locate element: {"method":"css selector",&…...

小程序需要进行软件测试吗?小程序测试有哪些测试内容?
在如今移动互联网快速发展的时代,小程序已成为人们生活中不可或缺的一部分。然而,面对日益增长的小程序数量和用户需求,小程序的稳定性和质量问题日益突显。因此,对小程序进行软件测试显得尤为重要。 近期的一项调查显示…...

一文读懂企业租用GPU的注意事项!
在人工智能、大数据处理及高性能计算领域,GPU算力已成为推动技术创新与业务增长的核心动力。尚云Sunclouds作为GPU算力租赁服务提供商,为用户提供了灵活、高效且成本可控的解决方案。对于初次接触GPU算力租赁的用户而言,了解并掌握租用过程中…...

Linux运维:mysql主从复制原理及实验
当一台数据库服务器出现负载的情况下,需要扩展服务器服务器性能扩展方式有向上扩展,垂直扩展。向外扩展,横向扩展。通俗的讲垂直扩展是将一台服务器扩展为性能更强的服务器。横向扩展是增加几台服务器。 主从复制好比存了1000块钱在主上&…...

022-GeoGebra中级篇-几何对象之直线与坐标轴
本文主要介绍一下GeoGebra中直线的常见输入方式,比如工具栏输入、表达式输入、函数输入,最后再把坐标轴的调用简单介绍一下。内容比起传统的教学更偏向于实战一些,若感兴趣欢迎继续阅读。 目录 一、直线1. 关于工具栏绘制(1&#…...

node js安装、配置(Windows版)
目录 node js 安装 node js 全局配置 1、全局安装路径 2、全局缓存路径 3、修改环境变量 pnpm安装、卸载 全局安装pnpm 验证pnpm版本 卸载pnpm 1、移除全局安装的包 2、移除pnpm cli 脚本直接安装 npm安装的使用命令直接卸载 node js 安装 cmd 查看是否存在&…...
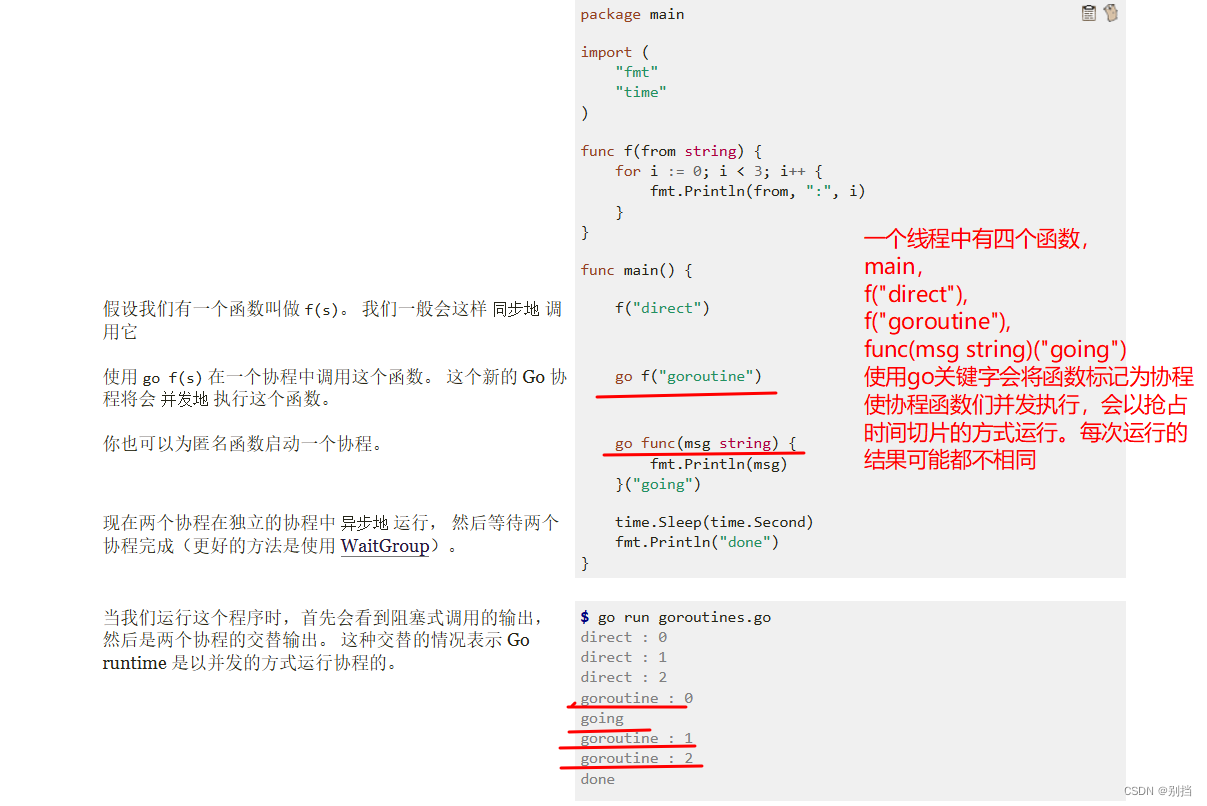
go语言day08 泛型 自定义错误处理 go关键字:协程
泛型: 抛错误异常 实现error接口类型 用java语言解释的话,实现类需要重写error类型的抽象方法Error().这样就可以自定义异常处理。 回到go语言,在Error()方法中用*argError 这样一个指针类来充当error接口的实现类。 在f2()方法中定义返回值…...

MySql性能调优01-[数据结构和索引]
数据结构和索引 什么是索引索引的种类常见索引数据结构和区别二叉树 红黑树 什么是索引 索引的种类 在Mysql中索引是在存储引擎层实现的,而不是在服务层实现的 按数据结构分:Btree索引、Hash索引、Full-text索引按存储结构分:聚簇索引、非聚…...

【算法入门-栈】逆波兰表达式求值
📖逆波兰表达式求值 ✅描述✅扩展:什么是逆波兰表达式✅题解方法一:栈✅题解方法二(数组模拟栈) 今天又刷了一道题,奥利给 刷题地址: 点击跳转 ✅描述 给定一个逆波兰表达式,求表达…...

【史上最全面ESP32教程】http通信
文章目录 前言HTTP协议是什么?HTTP协议的特点HTTP协议的常见应用 esp32 使用http通信通信流程基础使用HTTPClient 常用的函数函数介绍:void end(void);bool connected(void);void setReuse(bool reuse);void setUserAgent(const String& userAgent);…...
第二十七天 | 56. 合并区间、738. 单调递增的数字、968. 监控二叉树)
*算法训练(leetcode)第二十七天 | 56. 合并区间、738. 单调递增的数字、968. 监控二叉树
刷题记录 56. 合并区间*738. 单调递增的数字*968. 监控二叉树 56. 合并区间 leetcode题目地址 排序后遇到有重合的区间选择最大的区间保存即可,结果集中保存的是离当前区间最近的区间,因此使用当前区间与结果集中的最后一个集合比较查看是否有重合&…...

OpenJudge 奇数求和
目录 描述思路样例输入样例输出CodeCC 总时间限制: 1000ms 内存限制: 65536kB 描述 计算非负整数 m 到 n(包括m 和 n )之间的所有奇数的和,其中,m 不大于 n,且n 不大于300。例如 m3, n12, 其和则为:357911…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...
