Java——二叉树的最近公共祖先及二叉搜索树介绍
目录
二叉树的最近公共祖先
题目
思路一:如果给定的是一颗二叉搜索树,
思路二:假设是孩子双亲表示法
二叉搜索树
定义Node类
查找
删除
插入
二叉树的最近公共祖先
题目
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”

提示:
树中节点数目在范围 [2, 105] 内。
-109 <= Node.val <= 109
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中
思路一:如果给定的是一颗二叉搜索树,
二叉搜索树:中序遍历的大小是有序的,根节点的左树都比根节点的小,根节点的右树都比根节点大。
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {//先根据二叉搜索树来写if(root==null) return null;if(root==p||root==q) return root;TreeNode leftT=lowestCommonAncestor(root.left,p,q);TreeNode rightT=lowestCommonAncestor(root.right,p,q);if(leftT!=null&&rightT!=null){return root;}else if(leftT!=null){return leftT;}else{return rightT;}} }
思路二:假设是孩子双亲表示法
就相当于链表求交点,但是我们的表示中没有双亲结点,因此我们引入两个栈。
1.用两个栈 存储root->q,root->p的路径;
2.求栈的大小;
3.让栈中多的元素出差值个元素;
4.开始出栈,直到栈顶元素相同,就是公共祖先;
如何去找到从根节点到一个指定节点的路径?
class Solution {//root根结点,node:指定的节点,stack:存放根节点到指定节点的路径public boolean getPath(TreeNode root,TreeNode node ,Stack<TreeNode> stack){if(root==null||node==null) return false;stack.push(root);if(node==root) return true;boolean flg=getPath(root.left,node,stack);if(flg==true) return true;//找到啦flg=getPath(root.right,node,stack);if(flg==true) return true;//找到啦stack.pop();return false;}public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if(root==null) return null;Stack<TreeNode> stack1=new Stack<>();getPath(root,p,stack1);Stack<TreeNode> stack2=new Stack<>();getPath(root,q,stack2);int size1=stack1.size();int size2=stack2.size();if(size1>size2){int size=size1-size2;while(size!=0){stack1.pop();size--;}while(!stack1.isEmpty()&&!stack2.isEmpty()){//直接判断地址if(stack1.peek()==stack2.peek()){return stack1.pop();}else{stack1.pop();stack2.pop();}}}else{int size=size2-size1;while(size!=0){stack2.pop();size--;}while(!stack1.isEmpty()&&!stack2.isEmpty()){//直接判断地址if(stack1.peek()==stack2.peek()){return stack2.pop();}else{stack1.pop();stack2.pop();}}}return null;} }
二叉搜索树
是空树或者:若它的左子树不为空,则左子树上所有节点的值都小于根节点的值若它的右子树不为空,则右子树上所有节点的值都大于根节点的值它的左右子树也分别为二叉搜索树
定义Node类
class Node{public int val;public Node left;public Node right;public Node(int val){this.val=val;}
}查找
public Node root=null;public Node search(int key){Node cur = root;if(cur.val<key){cur = cur.right;}else if(cur.val>key){cur = cur.left;}else{return cur;}return null;}删除
设待删除结点为 cur, 待删除结点的双亲结点为 parent1. cur.left == null1. cur 是 root,则 root = cur.right2. cur 不是 root,cur 是 parent.left,则 parent.left = cur.right3. cur 不是 root,cur 是 parent.right,则 parent.right = cur.right2. cur.right == null1. cur 是 root,则 root = cur.left2. cur 不是 root,cur 是 parent.left,则 parent.left = cur.left3. cur 不是 root,cur 是 parent.right,则 parent.right = cur.left3. cur.left != null && cur.right != null1. 需要使用替换法进行删除,即在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点中,再来处理该结点的删除问题
//要删除节点,你需要知道这个节点的父节点//当要删除的节点的左节点为空//一般删除节点都是删除叶子节点public void f(Node cur,Node parent){if(cur.left==null){//当删除的节点左边没有节点if(cur==root){root=cur.right;}else if(cur==parent.left){parent.left=cur.right;}else{parent.right=cur.right;}}else if(cur.right==null){if(cur==root){root=cur.left;}else if(cur==parent.left){parent.left=cur.left;}else{parent.right=cur.left;}}else{//左右节点都不是空//相当于在右树中找一个较小值换到那个位置//或者就是在左树中找较大值//Node targetParent=cur;Node target=cur.right;while(target.left!=null){targetParent=target;target=target.left;}cur.val=target.val;if(target==targetParent.left){targetParent.left=target.right;}else{targetParent.right=target.right;}}}public void remove(int key){Node cur=root;Node parent=null;while(cur!=null){if(cur.val==key){f(cur,parent);break;}else if(cur.val<key){parent=cur;cur=cur.right;}else{parent=cur;cur=cur.left;}}}插入
//二叉搜索树插入的数据一定是在叶子节点//1.cur,parent来找到val需要存储的位置//2.parent.val比较大小,确定格式在左边还是右边进行插入public boolean insert(int val){if(root == null){root = new Node(val);return true;}Node cur = root;Node parent = null;//找到parent的位置while(cur!=null){if(cur.val<val){parent=cur;cur=cur.right;}else if(cur.val==val){//bureturn false;}else{parent=cur;cur=cur.left;}}//找到对应位置开始插入Node node=new Node(val);if(parent.val<val){parent.right=node;}else{parent.left=node;}return true;}相关文章:
Java——二叉树的最近公共祖先及二叉搜索树介绍
目录 二叉树的最近公共祖先 题目 思路一:如果给定的是一颗二叉搜索树, 思路二:假设是孩子双亲表示法 二叉搜索树 定义Node类 查找 删除 插入 二叉树的最近公共祖先 题目 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百…...

Stable Diffusion加chilloutmixni真人图片生成模型,AI绘图杀疯了
上期图文教程,我们分享过AI绘图大模型Stable Diffusion以及中文版本文心AI绘画大模型的基础知识以及代码实现,截至到目前为止。Stable Diffusion模型已经更新到了V2.1版本,其文生图大模型也越来越火,其在2022年底,由AI绘制的图片被荣为国际大奖,让大家对AI绘画大模型也越…...

Matplotlib 绘图实用大全
本文只介绍最简单基本的画图方法 预设 要想画出来的图有些逼格,首先应该进行如下设置 plt.rcParams[font.sans-serif][SimHei] #画图时显示中文字体 plt.rcParams[axes.unicode_minus] False #防止因修改成中文字符,导致某些 unicode 字符不能…...
MyBatis源码用了哪些设计模式?
MyBatis源码用了哪些设计模式?前言一、创建型模式工厂模式单例模式建造者模式二、结构型模式适配器模式代理模式组合模式装饰器模式三、行为型模式模板模式策略模式迭代器模式总结前言 在 MyBatis 的两万多行的框架源码中,使用了大量的设计模式对工程架…...

【16.整数转罗马数字】
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。 字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M 1000 例…...

前端小技巧
1.html 1.1 网站自动刷新 应用场景: 网页定期自动刷新(现在基本淘汰了,采用ajax);自动跳转到指定页面,这个自动跳转的好处就是不需要JS调用,属于纯html网页自动跳转 v7-网站自动刷新 你可以…...
Servlet2.0
文章目录更方便的部署方式安装插件使用插件验证程序常见访问出错的解决方案404错误405错误500错误空白页面无法访问此网站在文章 TomcatServlet初识中,我们通过七个大的步骤才可以完成一个简单的Servlet程序,这个过程无疑是非常繁琐的,那么我…...

【c++】继承
目录 一、继承的表现 子类对父类成员的访问权限 二、父类与子类之间的相互赋值 三、继承的作用域 如果是父类和子类构成隐藏呢? 四、子类的成员函数怎么写 1.default构造函数 2.析构函数 所以析构函数不需要我们显式调用。 五、继承与友元函数 六、继承与静…...

minio安装配置和使用(二)客户端安装
安装minio客户端mcli 命令如下: dnf install https://dl.minio.org.cn/client/mc/release/linux-amd64/mcli-20230128202938.0.0.x86_64.rpm 安装完成,在/usr/local/bin/下新增了mcli命令 mcli是对minio进行管理的命令。功能丰富, 基本格式…...

【如何使用Arduino设置GRBL和控制CNC机床】
【如何使用Arduino设置GRBL和控制CNC机床】 前言1. 什么是GRBL?2. 所需硬件3. 如何安装GRBL4. GRBL 配置5. GRBL 控制器5.1 如何使用通用 G 代码发送器5.2 波特率5.3 电机方向5.4 步进比例系数5.5 限位开关5.6 数控机床的归位设置6. 结论前言 如果您正在考虑或正在制造自己的…...
项目测试——博客系统
文章目录项目测试——博客系统项目简介项目功能测试计划web自动化测试1. 测试用例2.web自动化测试说明项目测试——博客系统 项目简介 博客系统主要分为8大模块,分别是注册页,登录页,编辑页,修改页,个人主页…...
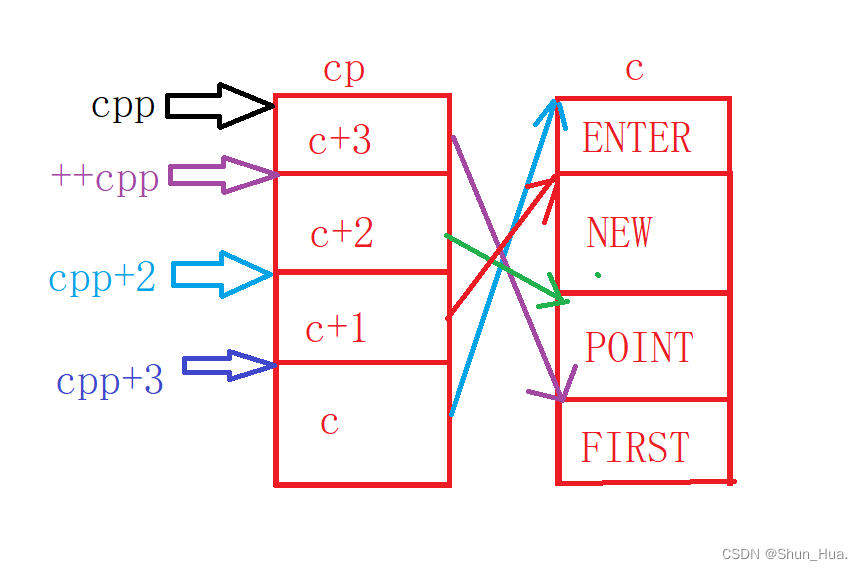
【C习题】经典数组与指针面试题(万字)
文章目录一. 一维数组二.字符数组三.字符指针四.二维数组五.指针笔试题一. 一维数组 首先说明:需熟记以下三个规则。 规则1.&数组名指的是取出整个数组的地址。 规则2.数组名被单独放在sizeof内部,计算的是整个数组的大小。 说明:这里的单…...
【ArcGIS Pro二次开发】(13):ProWindow的用法
ProWindow是ArcGIS Pro SDK中的一个WPF控件,具有以下特点: 可扩展性:ProWindow提供了丰富的API和样式,可以轻松地扩展和自定义ArcGIS Pro应用程序的UI。 可定制性:ProWindow支持多种UI控件和布局方式,可以…...

HTML/CSS/JS 基本语法
前端一、HTNL1、文件结构2、文本标签(1)块元素:div(2)行内元素:span(3)格式标签3、图片、音频、视频(1)图片(2)音频< audio >&a…...

对于从事芯片行业的人来说,有哪些知识是需要储备的?
近两年芯片行业大火,不少同学想要转行,却不知道该如何下手,需要学习哪些基础知识,下面就来看看资深工程师怎么说? 随着工艺的发展,芯片肯定是尺寸越来越小,至于小到什么样的程度是极限…...

测试场景设计
测试场景设计 又叫做场景法。其实对于场景法是测试用例中面临最多的,但是这种模式不是很容易总结,有时候是基于经验,有时候是我们对系统的了解。所以在这种情况下,我们强硬的用场景法对其进行规范。 场景法原理 现在的软件几乎…...
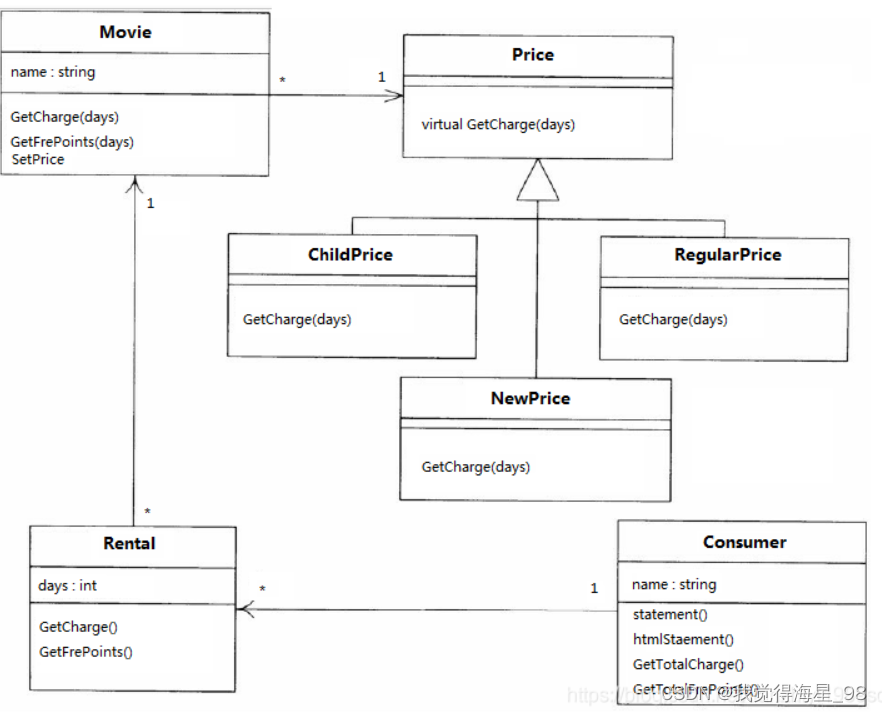
《重构》增强代码可读性
文章目录重构原则何为重构为何重构何时重构重构会影响性能吗实例原始类进行重构分解statements方法提取函数搬移函数提炼“积分计算”功能去除临时变量(以查询取代临时变量)运用多态取代与价格相关的条件逻辑代码迁移Movie类Price类 状态模式搬移函数以多…...

数据分析自学路线
数据分析作为近几年火起来的IT技术岗位,在大数据时代的浪潮下迅速发酵膨胀,席卷了众多互联网企业,漫延到了金融、教育、医疗、消费等传统行业,在新经济领域也有重要作用,比如人工智能、新能源、电子芯片、企业数字化服…...

蓝桥杯C++组怒刷50道真题
🌼深夜伤感网抑云 - 南辰Music/御小兮 - 单曲 - 网易云音乐 🌼多年后再见你 - 乔洋/周林枫 - 单曲 - 网易云音乐 50题才停更,课业繁忙,有时间就更,2023/3/14/15:06写下 目录 👊填空题 🌼一…...

【期末小作业】HTML、CSS前端静态网页
分享一个可以“趁别人喝咖啡的功夫“”写的一个静态网页,纯纯练手小项目,适合前端刚入门的小白练练手。 前端练手静态页面 实现效果图展示 CSS代码 HTML 代码 环境:VScode编辑器 语言:HTML 、CSS 一、实现效果图 仅仅通过…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

