【排序 - 归并排序】
归并排序(Merge Sort)是一种高效的排序算法,基于分治(Divide and Conquer)策略。它将待排序数组分成两个较小的子数组,分别对它们进行排序,然后将排好序的子数组合并成一个整体有序的数组。归并排序的时间复杂度为O(n log n),在大多数情况下是最佳选择之一。
归并排序的原理
归并排序的过程可以分为两个主要步骤:分解和合并。
- 分解:将原始数组递归地分解为较小的子数组,直到每个子数组只有一个元素。
- 合并:将两个已排序的子数组合并成一个有序的数组,不断重复这个过程直到整个数组排序完成。

归并排序的算法步骤
-
分解:
- 将待排序数组分为两个大致相等的子数组。
- 递归地对每个子数组进行归并排序,直到子数组长度为1。
-
合并:
- 合并两个已排序的子数组为一个新的有序数组。
- 将两个子数组的元素逐个比较,依次放入新数组中,直到将两个子数组全部合并。
-
递归结束条件:
- 当子数组长度为1时,递归结束。
归并排序的C语言实现
下面是归并排序的C语言实现示例:
#include <stdio.h>
#include <stdlib.h>// 归并函数,用于将两个已排序的数组合并为一个有序数组
void merge(int arr[], int left, int mid, int right) {int i, j, k;int n1 = mid - left + 1; // 左子数组的大小int n2 = right - mid; // 右子数组的大小// 创建临时数组int L[n1], R[n2];// 将数据复制到临时数组 L[] 和 R[] 中for (i = 0; i < n1; i++)L[i] = arr[left + i];for (j = 0; j < n2; j++)R[j] = arr[mid + 1 + j];// 归并临时数组到 arr[left..right]i = 0; // 初始化左子数组的索引j = 0; // 初始化右子数组的索引k = left; // 初始化归并子数组的索引while (i < n1 && j < n2) {if (L[i] <= R[j]) {arr[k] = L[i];i++;} else {arr[k] = R[j];j++;}k++;}// 复制 L[] 的剩余元素(如果有)while (i < n1) {arr[k] = L[i];i++;k++;}// 复制 R[] 的剩余元素(如果有)while (j < n2) {arr[k] = R[j];j++;k++;}
}// 归并排序函数
void mergeSort(int arr[], int left, int right) {if (left < right) {int mid = left + (right - left) / 2; // 避免溢出mergeSort(arr, left, mid); // 对左半部分进行归并排序mergeSort(arr, mid + 1, right); // 对右半部分进行归并排序merge(arr, left, mid, right); // 合并已排序的子数组}
}// 打印数组的函数
void printArray(int arr[], int size) {int i;for (i = 0; i < size; i++)printf("%d ", arr[i]);printf("\n");
}// 主函数
int main() {int arr[] = {12, 11, 13, 5, 6, 7};int arr_size = sizeof(arr) / sizeof(arr[0]);printf("原始数组:\n");printArray(arr, arr_size);mergeSort(arr, 0, arr_size - 1);printf("排序后的数组:\n");printArray(arr, arr_size);return 0;
}
总结
归并排序是一种效率高且稳定的排序算法,适用于大规模数据集的排序需求。通过递归地分解和合并数组,归并排序可以在O(n log n)的时间复杂度内完成排序,因此在实际应用中被广泛使用。通过本文的介绍和C语言实现示例,读者可以更深入地理解归并排序的工作原理和实现方式。
相关文章:

【排序 - 归并排序】
归并排序(Merge Sort)是一种高效的排序算法,基于分治(Divide and Conquer)策略。它将待排序数组分成两个较小的子数组,分别对它们进行排序,然后将排好序的子数组合并成一个整体有序的数组。归并…...

Appium元素定位(全网详细讲解)(二)
1.appium inspector(定位元素的工具)使用方法 详细介绍: 详细解释: 图标名称说明1Show Element Handles是否显示元素句柄2Select Elements选择元素定位3Tap/Swipe By Coordinates按坐标点击/滑动4Download Screenshot下载屏幕截…...

滑动窗口,最长子序列最好的选择 -> O(N)
最近在学校上短学期课程,做程序设计题,一下子回忆起了大一学数据结构与算法的日子! 这十天我会记录一些做题的心得,今天带来的是对于最长子序列长度题型的解题框架:滑动窗口 本质就是双指针算法: 通过le…...

【Python】已解决:Python安装过程中的报错问题
文章目录 一、分析问题背景二、可能出错的原因三、错误代码示例四、正确解决方法五、注意事项 已解决:Python安装过程中的报错问题 一、分析问题背景 在安装Python 3.9.6(64位)版本时,用户可能会遇到一个报错信息,提…...

C++ STL IO流介绍
目录 一:IO流的继承关系: 二:输入输出功能 1. 基本用法 2. 格式化输入 3.非格式化输入 4. 格式化输出 三:流 1. 字符流 2. 向字符流中写入数据 3. 从字符流中读出数据 4. 清空字符流 5.完整的例子 四:文件…...

华为浏览器,Chrome的平替,插件无缝连接
文章目录 背景插件书签 背景 不知道各位小伙伴有没有这样的痛点,办公电脑、家里的电脑还有手机、平板等,收藏了一个网址或者在手机上浏览了某个网页,保存起来,可是一换平台或者换个电脑,在想要浏览之前收藏的东西&…...

SpringBoot新手快速入门系列教程:前述
我自己是一个SpringBoot新手,花了一天时间学了SpringBoot。大家不要惊讶,前提是我自己已经有了10几年的编程经验精通多门语言,并且在人间最强兵器Chat某T的AI助手帮助下,才能创造一天快速学会一个框架的神话。 当然中间遇到了很多…...

C语言9 指针
目录 指针的声明与初始化 指针运算 指针的加法和减法 指针的比较 指针与数组 通过指针访问数组元素 指针与多维数组 声明指向多维数组的指针 访问多维数组元素 指针数组和数组指针 指针数组 数组指针 字符指针 字符串的定义和字符指针 直接使用字符指针初始化字…...

Floyd判圈算法——寻找重复数(C++)
287. 寻找重复数 - 力扣(LeetCode) 题目描述 给定一个包含 n 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。假设 nums 只有 一个重复的整数 ,返…...

面试题目分享
学习目标: 从面试了解自己的不足。 学习内容: 1.你会什么语言? 我该如何回答,我会java,c,c等,在工作中我会用到合适的语言。 牛逼吹的大话 尊敬的面试官,我精通Java和Python&…...

Solana开发之Anchor框架
文章目录 Solana开发之Anchor框架一、什么是Anchor二、安装和使用1. 安装rust2. 安装Solana下载预构建的二进制文件 3. 使用 Anchor 版本管理器 (avm) 进行安装(推荐) 四、Anchor 核心原理Anchor 程序由三部分组成程序的 ID 从哪里…...

界面组件Kendo UI for React 2024 Q2亮点 - 生成式AI集成、设计系统增强
随着最新的2024年第二季度发布,Kendo UI for React为应用程序开发设定了标准,包括生成式AI集成、增强的设计系统功能和可访问的数据可视化。新的2024年第二季度版本为应用程序界面提供了人工智能(AI)提示,从设计到代码的生产力增强、可访问性…...

python输出/sys/class/power_supply/BAT0/电池各项内容
读取 /sys/class/power_supply/BAT0/ 目录下的所有相关文件,并输出其内容: import os# 定义电池信息文件的路径 battery_path = "/sys/class/power_supply/BAT0/"# 读取文件内容的函数 def read_battery_info(file_name):try:with open(os.path.join(battery_path…...

HDFS体系架构文件写入/下载流程
HDFS体系架构 HDFS(Hadoop Distributed File System,Hadoop分布式文件系统)是Hadoop项目中的一个核心组件,旨在以高容错、高吞吐量来处理大规模数据集。它的体系架构由以下几个主要部分组成:Client,NameNo…...

大模型之战进入新赛季,开始卷应用
最近一段时间,国产大模型Kimi彻底火了,而这波爆火,某种意义上也展示了一个问题,即大模型的落地场景可能比技术比拼,更重要。 国产大模型Kimi突然爆火,与Kimi相关的产业链甚至被冠上“Kimi概念股”之名&…...
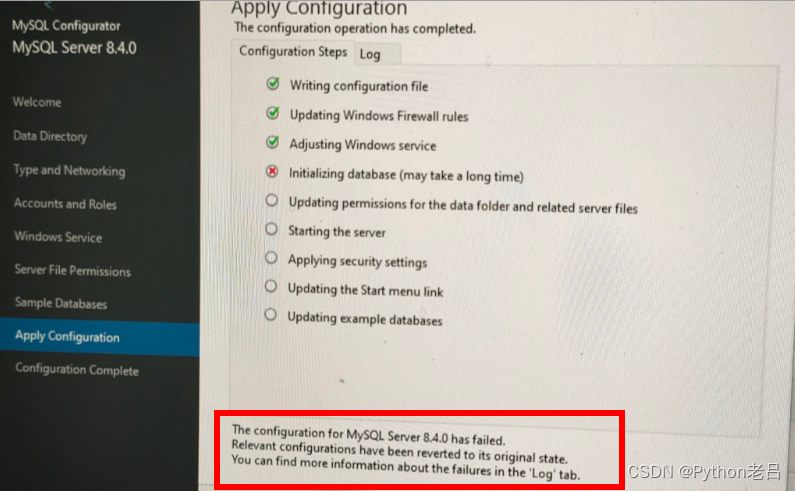
MySQL8.4.0 LTS安装教程 【小白轻松上手2024年最新长期支持版本MySQL手把手保姆级Windows超详细图文安装教程】
MySQL8.4.0 LTS安装教程 【小白轻松上手2024年最新长期支持版本MySQL手把手保姆级Windows超详细图文安装教程】 MySQL8.4.0前言(版本说明)官网下载MySQL1.访问MySQL官网2. 打开MySQL官网下载页面3. 选择下载类型Select Version【MySQL版本号】Select Ope…...

Linux 例题及详解
1.(yum)以下描述正确的是 A.在Centos中可以使用yum install 命令安装软件包 B.在Centos中可以使用yum uninstall 命令卸载软件包 C.在Centos中可以使用yum list 查看所有可安装软件包 D.在Centos中可以使用yum show查看所有可安装软件包 选项A、C是正确…...

爆款文案管理系统设计
设计一个爆款文案管理系统,目标是帮助营销团队高效地创建、管理并分析吸引人的文案,以提升产品或服务的市场吸引力和销售转化率。以下是一些关键功能和设计考量点: 1. 用户友好界面 简洁直观的界面:确保系统界面清晰,…...

FPGA-Verilog-Vivado-软件使用
这里写目录标题 1 软件配置2 FPGA-7000使用2.1 运行启动方式 1 软件配置 编辑器绑定为Vscode,粘贴VS code运行文件的目录,后缀参数保持不变: 如: D:/Users/xdwu/AppData/Local/Programs/Microsoft VS Code/Code.exe [file name]…...

Ambari Hive 创建函数无权限
作者:櫰木 1、创建udf函数 参考文档:https://blog.csdn.net/helloxiaozhe/article/details/102498567 如果已经编写好,请使用自己的。如果没有请参考以上链接进行udf函数编写。 2、创建函数遇到的问题 由于集群开启了kerberos࿰…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...
