数据结构-二叉搜索树与红黑树
4.二叉搜索树
又叫二叉查找树、有序二叉树、排序二叉树。树中任意一个结点,其左子树的每个节点值都要小于该节点,其右子树的每个节点值都要大于该节点

作用:能够进行快速查找、插入、删除操作
4.1 二叉搜索树的时间复杂度
注:二叉搜索树的形态各异,故时间复杂度也不尽相同
这里重点分析查找的时间复杂度,因为不管删除、插入操作,都要先进行查找目标。
4.1.1 查找时间复杂度
4.1.1.1 一般情况
分析:查找目标节点都要先从根节点开始找
eg:这里我们查找下图 值为5的节点,根据二叉搜索树的特点,首先我们要从结点开始,由于5比10小走左边到6的位置,由于5比6小继续走左边到4的位置,而5比4大故走右边,这里就找到5了,这里一共进行了3次对比找到了5。其他节点的查找方法也是这样。

下图,2的几次方代表每层的最大节点数量,而这个次方就代表对比的次数

故从上面得到,查找的时间复杂度为O(logn),由于上面说过,进行插入、删除操作都要进行查找操作,故它们两的时间复杂度也为O(logn)
4.1.1.2 特殊情况

这种情况就从二叉树退化为了链表,而链表的时间复杂度为O(n),故它的时间复杂度也为O(n) 。
5.红黑树
5.1 概念
也是一种自平衡的二叉搜索树(BST),以前叫作平衡二叉B树
5.2 红黑树特质(红黑规则)
5.2.1 节点要么是红色,要么是黑色
5.2.2 根节点必须是黑色
5.2.3 叶子节点都是黑色的空节点(标为null的都是空节点)
5.2.4 红黑树中红色节点的子节点都是黑色
5.2.5 从任意节点到叶子节点的所有路径都包含相同数目的黑色节点

注:再添加或删除节点时,如果不符和这些性质会发生旋转,以达到所有性质,也就是说这五个性质都是为了保证红黑树的平衡。
5.3 红黑树时间复杂度
5.3.1 查找
红黑树也h是一个二叉搜索树,故时间复杂度为O(logn)
5.3.2 添加
添加搜先要从查找操作开始,因为需要查找到目标添加位置,时间复杂度为O(logn),添加完成后,为了保证满足红黑树的特质即规则,故需要进行时间复杂度为O(1)的旋转调整操作。故总时间复杂度为O(logn)。
5.3.3 删除
删除搜先要从查找操作开始,因为需要查找到目标添加位置,时间复杂度为O(logn),删除完成后,为了保证满足红黑树的特质即规则,故需要进行时间复杂度为O(1)的旋转调整操作。故总时间复杂度为O(logn)。
即查找、添加、删除都是O(logn)
相关文章:

数据结构-二叉搜索树与红黑树
4.二叉搜索树 又叫二叉查找树、有序二叉树、排序二叉树。树中任意一个结点,其左子树的每个节点值都要小于该节点,其右子树的每个节点值都要大于该节点 作用:能够进行快速查找、插入、删除操作 4.1 二叉搜索树的时间复杂度 注:二…...

52771-009P 同轴连接器
型号简介 52771-009P是Southwest Microwave的连接器。这款连接器外导体外壳、耦合螺母和电缆夹紧螺母都采用了不锈钢 UNS-S30300 材料。不锈钢具有优异的耐腐蚀性和机械强度,能够保证连接器在各种恶劣环境下都能稳定工作。 型号特点 中心触点、外壳、衬套固定环&am…...

鸿蒙语言基础类库:【@ohos.util.Vector (线性容器Vector)】
线性容器Vector 说明: 本模块首批接口从API version 8开始支持。后续版本的新增接口,采用上角标单独标记接口的起始版本。开发前请熟悉鸿蒙开发指导文档:gitee.com/li-shizhen-skin/harmony-os/blob/master/README.md点击或者复制转到。 Vect…...

使用Python绘制堆积面积图
使用Python绘制堆积面积图 堆积面积图效果代码 堆积面积图 堆积面积图是面积图的一种扩展,通过堆积多个区域展示不同类别数据的累积变化。常用于显示不同部分对整体的贡献。 效果 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pQbW4F…...

代码还原动态调试之 pstree 乘法变加法
乘法编译后,生成加法汇编,提升CPU执行效率; 406a: 85 ff test %edi,%edi // x ? 0406c: 0f 84 7e 00 00 00 je 40f0 <__sprintf_chkplt0x1980>*/int digits, div;if (x ! 0) {/*4072: 89 fd …...
)
C++:获取当前可执行核心数(开辟线程)
sysconf(_SC_NPROCESSORS_ONLN) 是一个在 POSIX 兼容系统上广泛使用的函数,它用于获取当前系统上可用的处理器(CPU 核心)的数量。这个函数是 sysconf 函数的一个特定调用,其中 _SC_NPROCESSORS_ONLN 是一个常量,指定了…...

【简历】吉林某985大学:JAVA实习简历指导,面试通过率相当低
注:为保证用户信息安全,姓名和学校等信息已经进行同层次变更,内容部分细节也进行了部分隐藏 简历说明 这份简历是一个顶级985吉林大学的同学投Java职位的简历。因为学校是顶级985,所以他的大厂简历通过率是比较高的,…...

C#中的MD5摘要算法与哈希算法
文章目录 一、哈希算法基础二、MD5 算法原理三、MD5摘要算法四、哈希算法五、C#实现示例MD5算法示例哈希算法示例字符串MD5值对比 六、总结 一、哈希算法基础 哈希算法是一种单向密码体制,它将任意长度的数据转换成固定长度的字符串。这种转换是不可逆的࿰…...

使用 python 构建企业级高可用海量爬虫调度系统
一、引言 在大数据时代,信息的获取与分析成为了企业决策的重要依据。对于营销行业而言,实时抓取和分析竞争对手动态、市场趋势以及用户反馈等数据,是制定有效策略的关键。然而,构建一个高可用的、能够处理海量数据的爬虫调度系统…...

IDEA常用技巧荟萃:精通开发利器的艺术
1 概述 在现代软件开发的快节奏环境中,掌握一款高效且功能全面的集成开发环境(IDE)是提升个人和团队生产力的关键。IntelliJ IDEA,作为Java开发者的首选工具之一,不仅提供了丰富的编码辅助功能,还拥有高度…...

GD32F303之CAN通信
1、CAN时钟 GD32F303主时钟频率最大是120Mhz,然后APB1时钟最大是60Mhz,APB2时钟最大是120Mhz,CAN挂载在APB1总线上面 所以一般CAN的时钟频率是60Mhz,这个频率和后面配置波特率有关 2、GD32F303时钟配置 首先我们知道芯片有几个时钟 HXTAL:高速外部时钟࿱…...

postgres 的dblink使用,远程连接数据库
一.安装下载 dblink create extension if not exists dblink 查看是否已经安装 select * from pg_extension;二.运行,查询数据 其中,第一个参数是dblink名字,也可以是连接字符串。 第二个参数是要执行的SQL查询语句。AS子句用于指定返回结…...

短视频矩阵系统是什么?怎么搭建短视频矩阵系统?一文了解矩阵模式
在数字时代,短视频已成为信息传播的新宠,而短视频矩阵系统则是品牌和个人在短视频领域取得突破的重要工具。那么,短视频矩阵系统究竟是什么?如何搭建这样一个高效的系统?它又能够解决哪些问题呢?本文将为您…...

查看centos硬盘大小
直接上命令 lsblk...
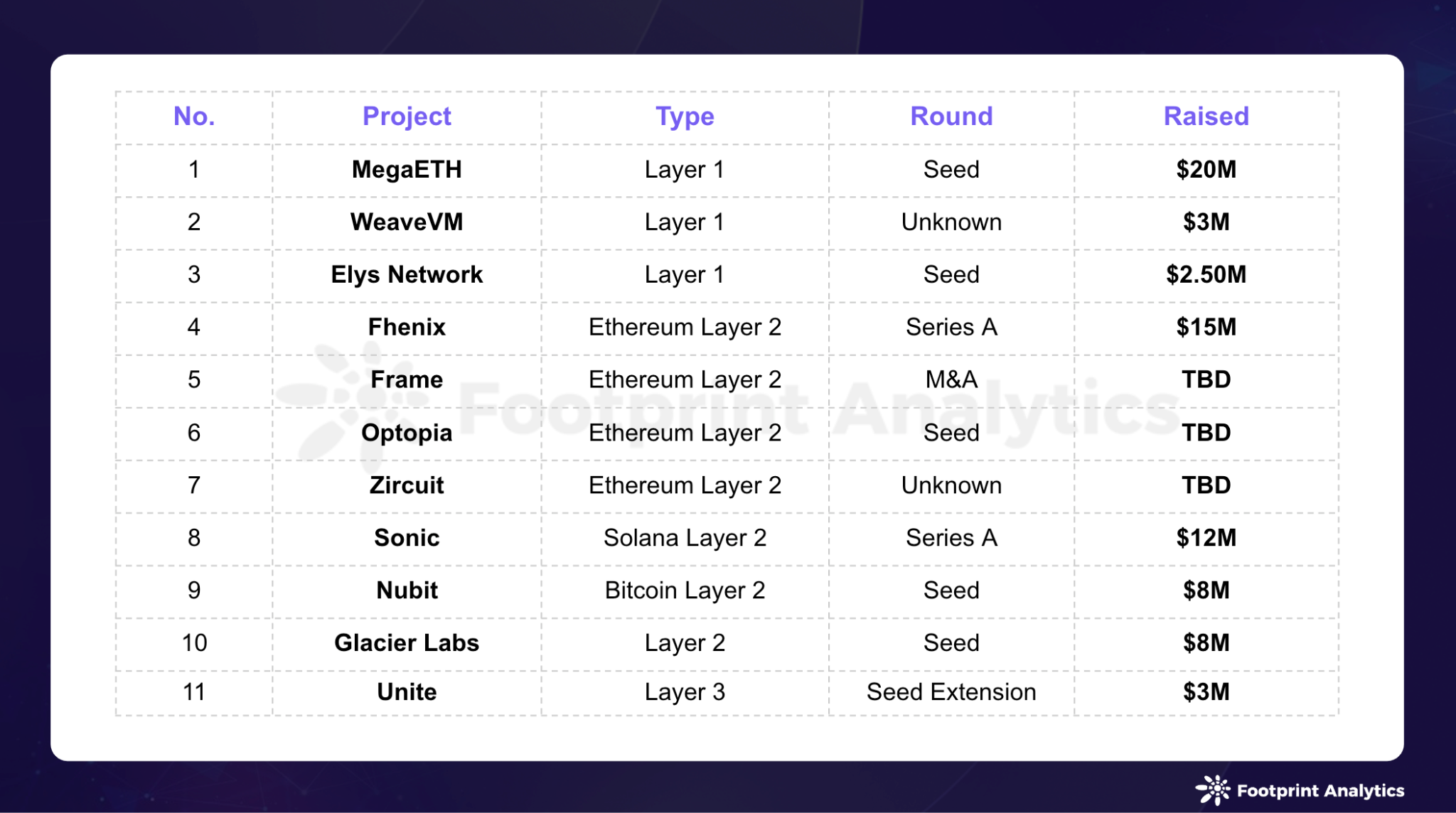
2024 年 6 月公链行业研报:市场回调,比特币和以太坊 Layer 2 表现各异
作者:stellafootprint.network 数据来源:公链 Research 页面 六月,加密货币市场经历了显著的挑战。比特币因即将到来的 Mt. Gox 赔偿支付及政府清算的压力,导致市场不确定性加剧。尽管美国现货以太坊 ETF 的推进带来了积极信号…...

SAP S4 销售组的定义和分配
spro-企业结构-定义-销售与分销-维护销售组 新增一个记录 spro-企业结构-分配-销售与分销-给销售办公室分配销售组...

实时数仓和离线数仓的区别是什么,企业该如何选择合适的数仓架构?
目录 一、离线数仓 1. 离线数仓是什么? 2. 离线数仓的特点 3. 离线数仓的适用场景 二、实时数仓 1. 实时数仓是什么? 2. 实时数仓的特点 3. 实时数仓的适用场景 三、由数仓需求变化带来的数据仓库架构的演变 1. 传统数仓架构 2. 离线大数据架构 3. Lambd…...

花所Flower非小号排名20名下载花所Flower
1、Flower花所介绍 Flower花所是一家新兴的数字货币交易平台,致力于为全球用户提供安全、便捷的交易体验。平台以其强大的技术支持和丰富的交易产品闻名,为用户提供多样化的数字资产交易服务,涵盖了主流和新兴数字货币的交易需求。 2. Flowe…...

程序员有哪些职位?
互联网行业中的岗位种类繁多、五花八门,学习一门技术后,重要的是找到合适的职业发展方向,程序员有哪些职业发展方向?一起来看看吧! 1.架构师 架构师需要程序员有强大的技术实力和深厚的技术积累。建筑师的成长需要经…...

python+Selenium自动化之免登录(cookie及token)
目录 cookie免登录 通过接口获取cookie 启用浏览器绕过登录 添加token 使用登录可以减去每次登录的重复操作,直接操作系统登录后的菜单页面,也可以减少安全验证登录,如图像验证登录的操作。注意:cookie和token都有有效期。 c…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...
