常见排序算法
/懂了和写出来是两码事啊啊......orz./
Talk is cheap, show me the code
一、快速排序
直接背模板就能过:
当x=q[l+r>>1]的边界情况
此时x取的是序列中间靠左的位置(如果序列个数为奇,则取正中间,如果为偶,则取中间靠左),此时如果元素个数为2,
则中间靠左就是第1个元素,这时就跟x=q[l]的边界情况一致了,所以这时只能用sort(l,j),sort(j+1,r);AcWing 785. 快速排序 - AcWing
#include <iostream> #include <cstring> #include <algorithm>using namespace std; const int N = 1e5 +10; int q[N],n; void quick_sort(int l,int r) {if(l>=r) return; //数组中只有一个或数组为空int x = q[l+r>>1];int i =l-1,j=r+1;while(i<j){do i++;while(q[i]<x);do j--;while(q[j]>x);if(i<j) swap(q[i],q[j]);}quick_sort(l,j);quick_sort(j+1,r);//此处是边界处理 } int main() {scanf("%d",&n);for(int i=0;i<n;i++) scanf("%d",&q[i]);quick_sort(0,n-1);for(int i =0;i<n;i++) printf("%d ",q[i]);return 0; }
扩展:第K个数活动 - AcWing
多家了一步,判断第k个数是在左边还是在右边,
在左边:区间长度,j-l+1>k,开始,l,结束,j,在区间中第k个数。
在右边:区间长度,j-l+1<k,开始,j+1,结束,r,在区间中第k -(j-l+1)个数。
#include <iostream> using namespace std; const int N = 1000010; int q[N];//返回值是int int quick_sort(int q[],int l,int r,int k)//要写int q[] {if(l>=r) return q[l];int i=l-1,j=r+1,x=q[(l+r)>>1];while(i<j){do i++;while(q[i]<x);do j--;while(q[j]>x);if(i<j) swap(q[i],q[j]);}if(j-l+1>=k) return quick_sort(q,l,j,k);else return quick_sort(q,j+1,r,k-(j-l+1));//判断k与j的大小,如果在左边就返回左边的数 } int main() {int n,k;scanf("%d%d", &n, &k);for (int i = 0; i < n; i ++ ) scanf("%d",&q[i]);cout << quick_sort(q,0,n-1,k)<<endl;return 0; }
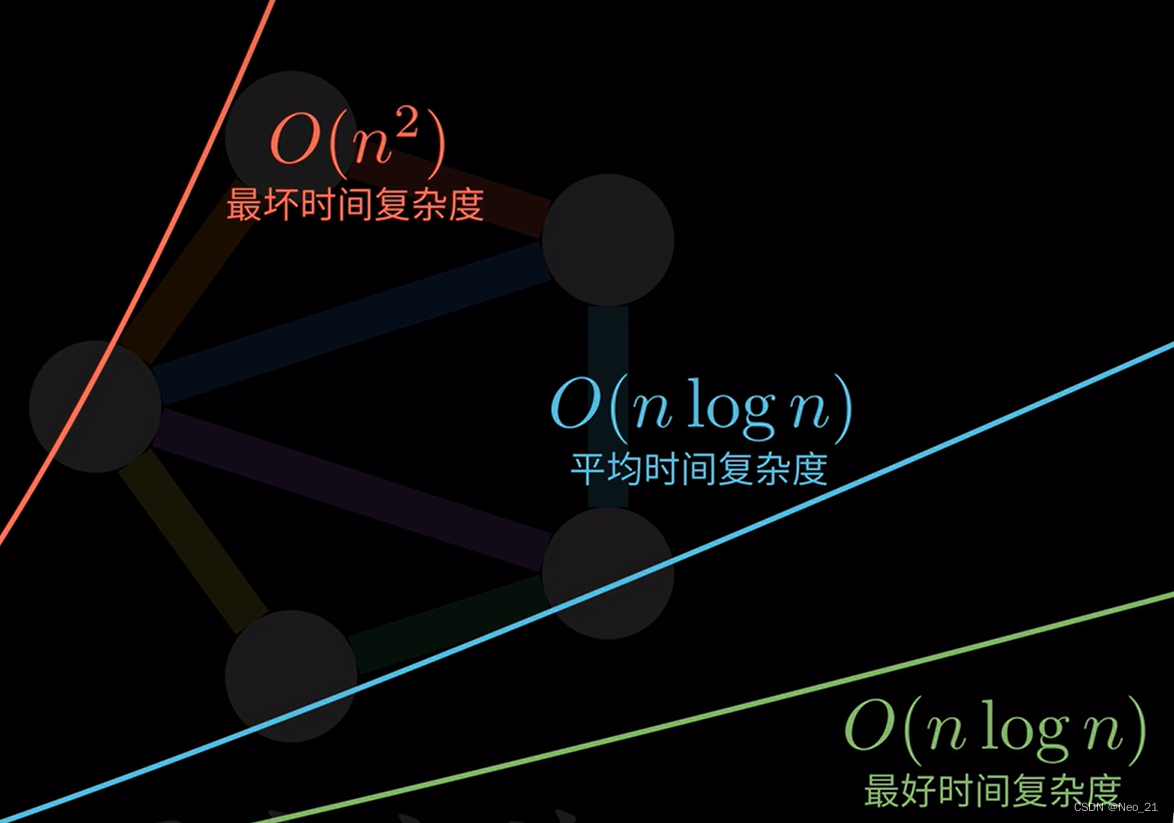
时间复杂度:
最坏:逆序的
二、归并排序
AcWing 787. 归并排序的证明与边界分析 - AcWing
时间复杂度:O(nlogn)
#include <iostream>
#include <cstring>
#include <algorithm>
const int N = 1e5+10;
int a[N],temp[N];
using namespace std;
void merge_sort(int q[],int l,int r)
{if(l>=r) return;int mid =(l+r)>>1;merge_sort(q,l,mid), merge_sort(q,mid+1,r);//递归时mid+1成为lint k =0,i=l,j=mid+1;while (i<=mid && j<=r){if(q[i]<q[j]) temp[k++]=q[i++];else temp[k++] = q[j++];}while(i<=mid) temp[k++]=q[i++];while(j<=r) temp[k++]=q[j++];for(int i =l,j=0;i<=r;i++,j++) q[i] = temp[j];}
int main()
{int n;scanf("%d", &n);for (int i = 0; i < n; i ++ ) scanf("%d",&a[i]);merge_sort(a,0,n-1);for (int i = 0; i < n; i ++ ) printf("%d ",a[i]);return 0;
}难一点的:求逆序对
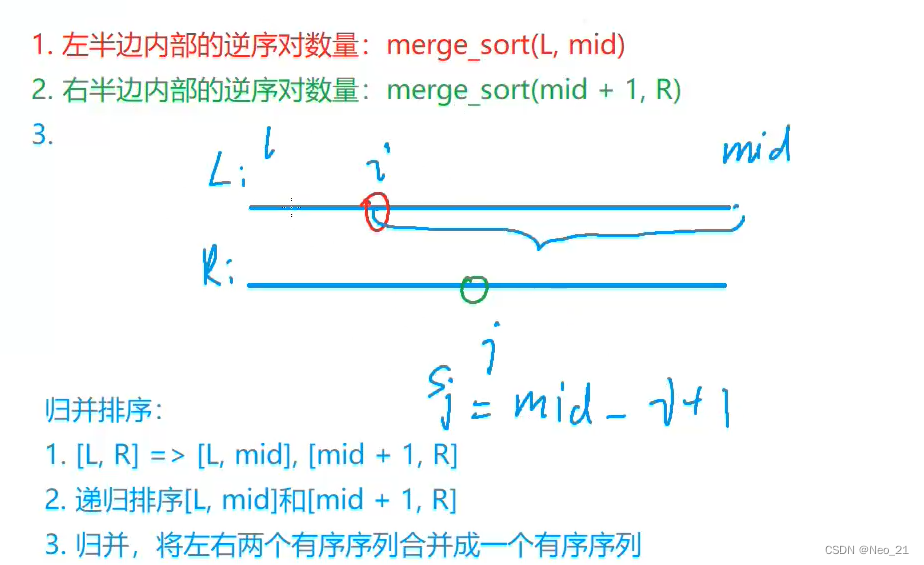
基本思路:设置一个mid,先求左半边内部和右半边内部的逆序对的数量:直接求
(两个数同时出现在左半边,或同时出现在右半边)
然后再用归并的思想,左半边的指针i,右半边的指针j。此时左半边和右半边都是有序的(从小到大),如果(i,j)是一对逆序对,那么在左半边有mid-l+1个关于j的逆序对。
AcWing 788. 逆序对的数量-要点 - AcWing
#include<iostream> using namespace std; const int N=1e5+10; int q[N], tmp[N]; int n; typedef long long LL;LL merge_sort(int l, int r){if(l>=r) return 0;LL s=0;int mid=l+r>>1;s=merge_sort(l, mid)+merge_sort(mid+1, r);int i=l, j=mid+1, k=0;while(i<=mid && j<=r){if(q[i]<=q[j]) tmp[k++]=q[i++];else {s+= mid-i+1;tmp[k++]=q[j++];}}while(i<=mid) tmp[k++]=q[i++];while(j<=r) tmp[k++]=q[j++];for(int i=l, k=0;i<=r;i++, k++) q[i]=tmp[k];return s; }int main(){cin>>n;for(int i=0;i<n;i++) scanf("%d", &q[i]);cout<<merge_sort(0, n-1) ;return 0;}
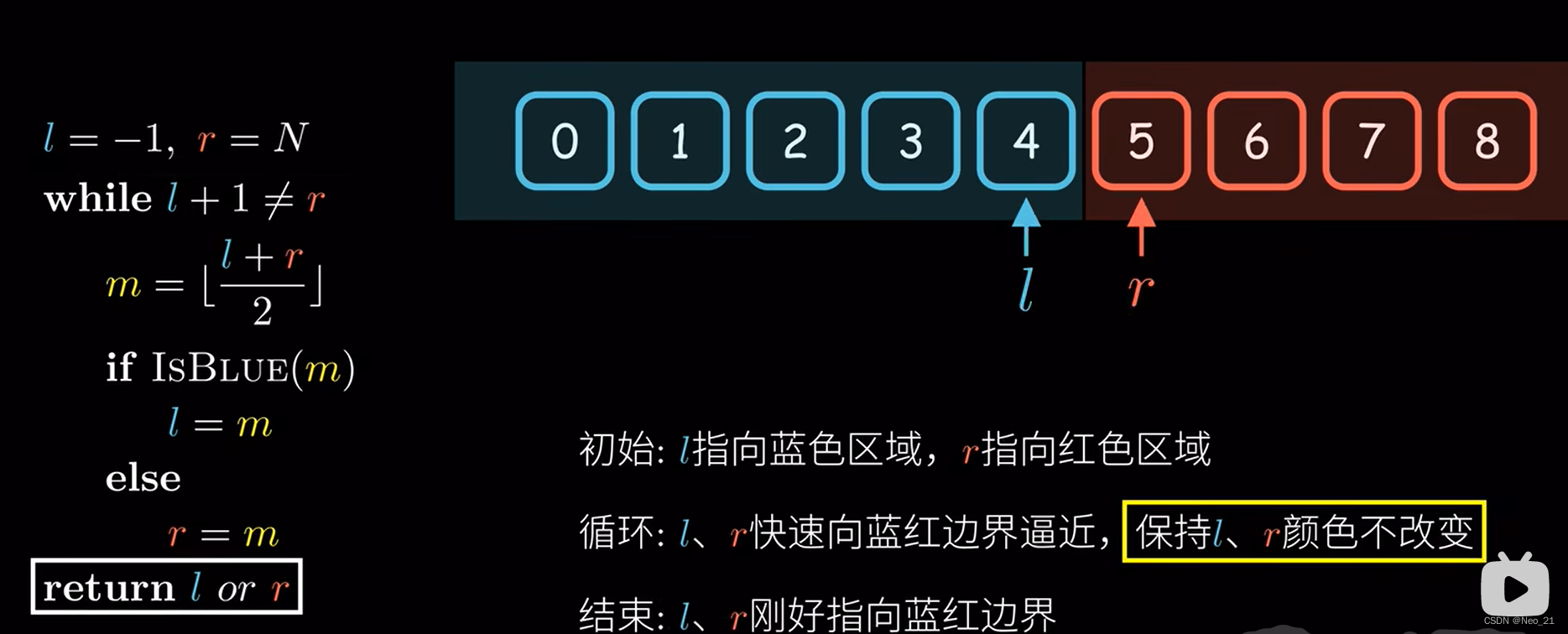
三、二分排序
整数二分
基本分治算法:AcWing 789. 二分算法的证明和边界分析 - AcWing
#include<iostream>
using namespace std;
const int N = 100010;
int n,m;//m个查询
int q[N];int main()
{scanf("%d%d", &n, &m);for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);while (m -- ){int x;//输入要查询的数scanf("%d",&x);int l=0,r=n-1;while(l<r)//寻找右边分界点,保证右边界点一直大于或等于x,然后左边靠近(else){int mid = l+r>>1;//向下取整if(q[mid]>=x) r = mid;//向左边缩小else l = mid+1;//向右边缩小}if(q[l]!=x) cout<<"-1 -1"<<endl;//不存在else{cout << l<<' ';//输出起始位置int l=0,r=n-1;while(l<r)//寻找左边分界点,保证左边界点一直小于或等于x,然后右边靠近{int mid = l+r+1>>1;//mid向上取整if(q[mid]<=x) l=mid;//else r =mid-1;}cout <<l <<endl;}}return 0;
}循环终止时, l >= r
易知 l不可能比 r 大 , 故 l = r, 根据循环不变式,l 就是答案点 res
另一种方法:(推荐使用)不需要考虑mid+1、mid-1的二分查找模板,希望大家都能学会_一支彩色铅笔csdn_一支彩色铅笔的博客-CSDN博客
时间复杂度:logn,因为指针每次移动都向边界移动
区域长度缩小一半。
细节点:
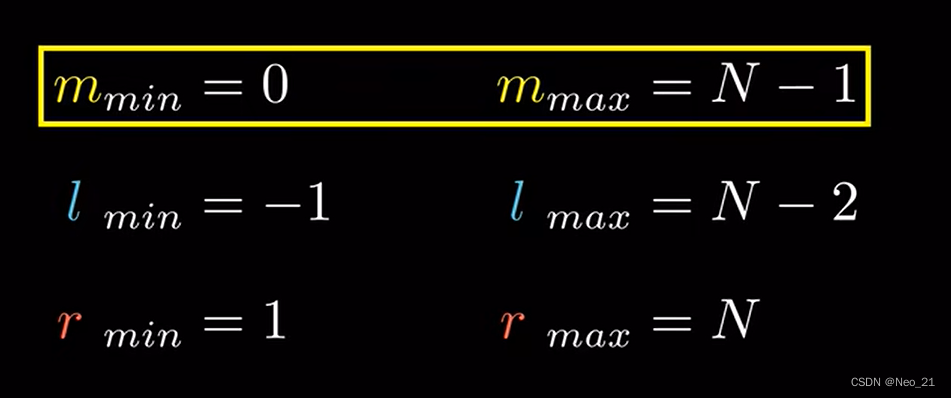
相关文章:
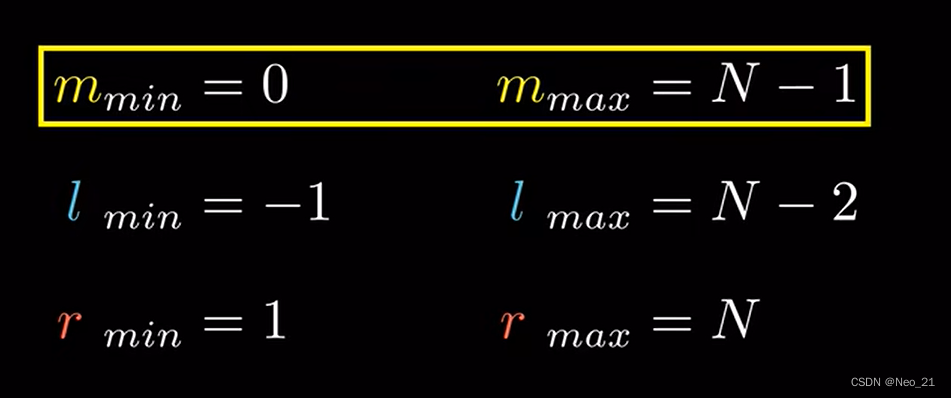
常见排序算法
/懂了和写出来是两码事啊啊......orz./ Talk is cheap, show me the code 一、快速排序 直接背模板就能过: 当xq[lr>>1]的边界情况 此时x取的是序列中间靠左的位置(如果序列个数为奇,则取正中间,如果为偶,则取中间靠左),此时如果元素个数为2, 则中间靠左就…...
C语言实现学生成绩管理系统思考
学生成绩管理系统思考 作业要求: 目录 思路 基本函数 学习理解大佬的代码: 完成作业: 思路 学生成绩管理系统,首先要初始化系统, 用C语言做学生实验管理系统要求实现对某班学生3门课程(包括语文、数…...
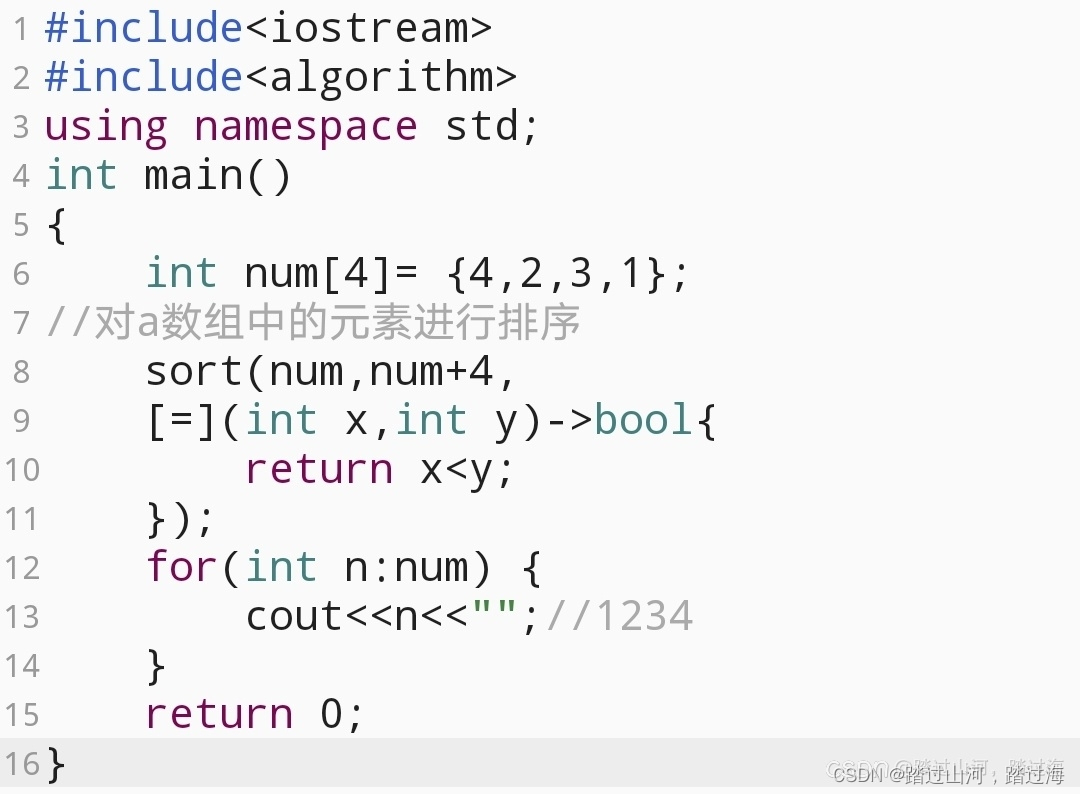
C++11中Lambda新特性
1.定义 lambda匿名函数的语法格式: [外部变量访问方式说明符](参数)mutablenoexcept/throw()->返回值类型 {函数体; };其中各部分的含义分别为: a.[外部变量方位方式说明符] []方括号用于向编译器表明当前是一个lambda表达式,其不能被省略…...
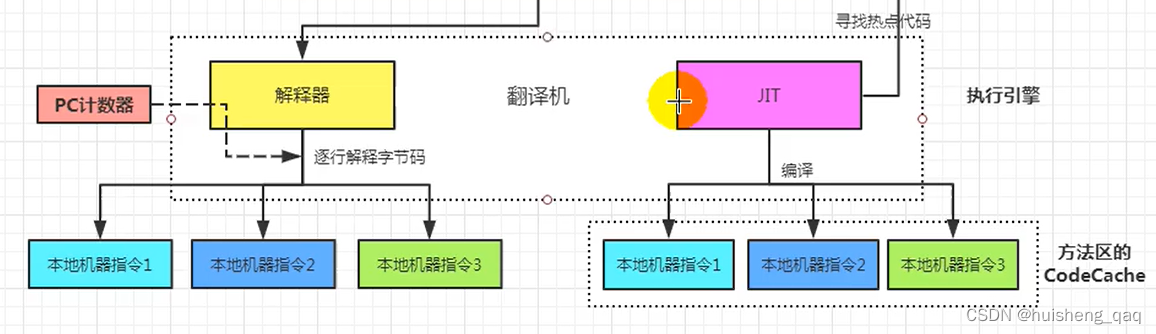
【jvm系列-01】初识虚拟机与java虚拟机
初识虚拟机与java虚拟机一,虚拟机与java虚拟机1,虚拟机2,java虚拟机3,jvm整体结构图4,jvm的架构模型5,jvm的生命周期6,jvm的种类划分6.1,Sun Classic Vm6.2,Exact VM6.3&…...

「Python 基础」数据库应用编程
Python 定义了一套 DB-API,任何数据库要连接到 Python,只需要提供符合 Python 标准的数据库驱动即可; 文章目录1. 连接 SQLite1. 建表、插入数据2. 查询数据2. 连接 MySQL1. 安装驱动2. 演示连接3. SQLAlchemy1. 安装2. DBSession3. add4. qu…...
一个nginx的小项目,不写代码,实现在局域网内访问其他电脑的网页
准备工作 下载nginx //官网 https://nginx.org/en/download.html //直接下载 https://nginx.org/download/nginx-1.23.3.zip解压 下载一个html项目,或者自己随便写一个 我是直接下载的,然后使用的是第一个01 https://gitee.com/StarPort/HTML_CSSTe…...

23.3.14打卡 2022年江西省大学生程序设计竞赛(正式赛)ABL
就写了签到, 其他题没写, 这场好像3题就银了 纪念一下3.14原粥率日 比赛链接:https://ac.nowcoder.com/acm/contest/43898 A题 Special Adjustment Method 题意 给出非负整数x, y, z 你可以让其中两个数字-1, 另外一个2, 使得x2y2z2x^2y^{2}z^{2}x2y2z2最大 题解 这题很容…...
用idea操作hbase数据库,并映射到hive
依赖条件:需要有Hadoop,hive,zookeeper,hbase环境映射:每一个在 Hive 表中的域都存在于 HBase 中,而在 Hive 表中不需要包含所有HBase 中的列。HBase 中的 RowKey 对应到 Hive 中为选择一个域使用 :key 来对…...
手机解锁方法:8个顶级的 Android 手机解锁软件
一般来说,太简单的密码是不安全的,所以我们设置一个安全的密码,可能会稍微复杂一点。然而,我们可能经常会忘记复杂的密码并锁定我们的 Android 智能手机。 8个顶级的 Android 手机解锁软件 如果您遇到过这种情况并且正在寻找一种…...
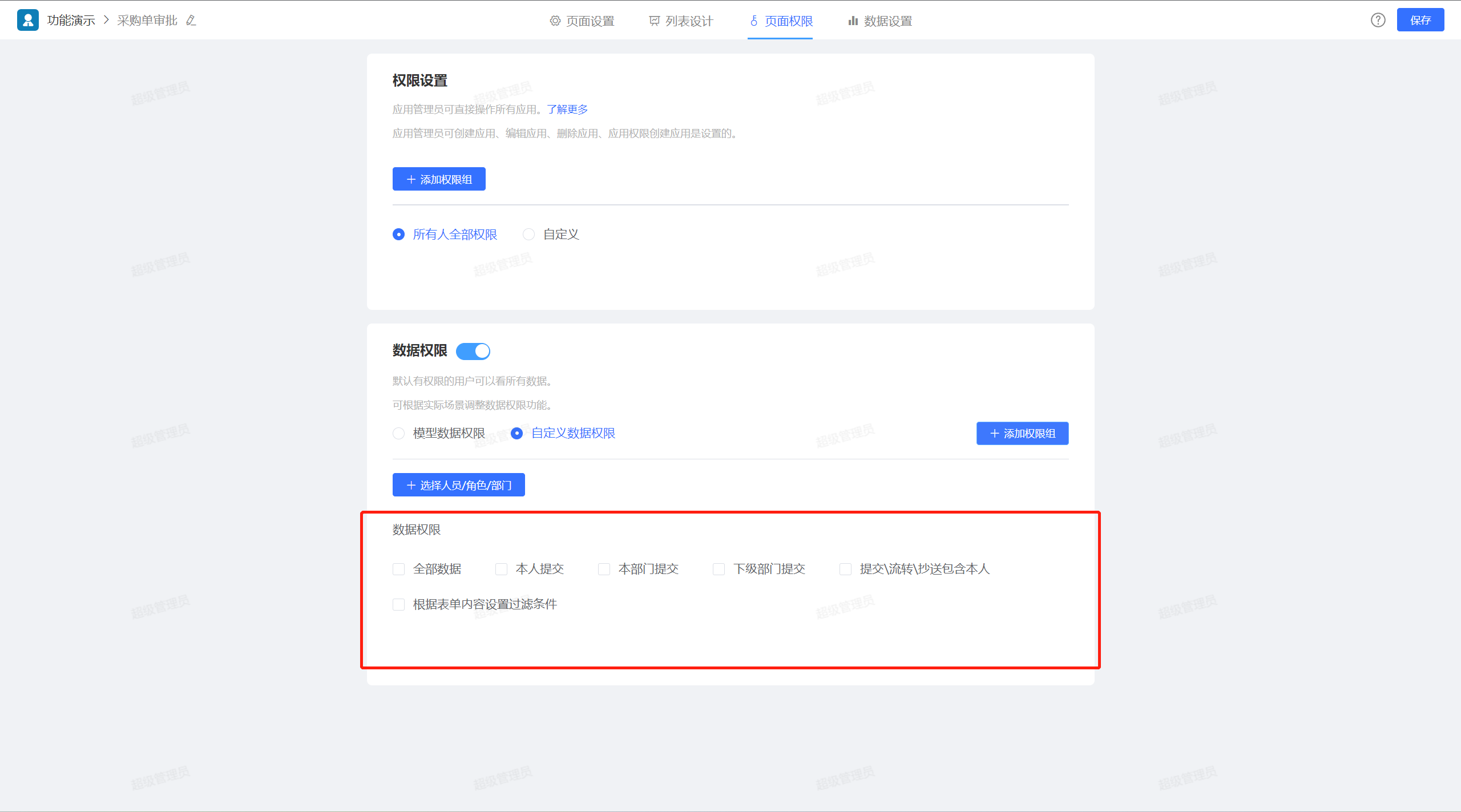
JVS快速开发平台2.1.7版本,列表页配置新增特性介绍
JVS 在3月份更新了2.1.7版本,本次更新涉及到很多方面,其中包括逻辑引擎、流程引擎、列表引擎、数据处理引擎、图表配置加工等。这里我们先介绍下列表页配置引擎扩展的相关内容,我们先来看看最后配置的列表页配置的效果1、列表页展示方面&…...
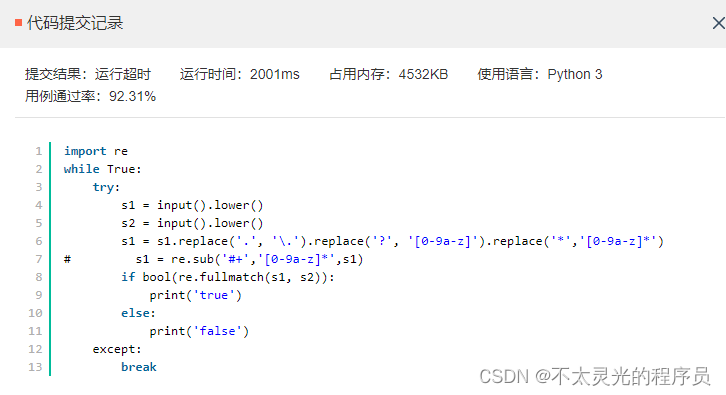
【华为机试真题详解 Python实现】去除多余空格【2023 Q1 | 100分】
文章目录 前言题目描述输入描述输出描述示例 1解题思路参考代码前言 《华为机试真题详解》专栏含牛客网华为专栏、华为面经试题、华为OD机试真题。 如果您在准备华为的面试,期间有想了解的可以私信我,我会尽可能帮您解答,也可以给您一些建议! 本文解法非最优解(即非性能…...

【SpringBoot项目实战+思维导图】瑞吉外卖⑤(新增套餐、套餐分页查询、删除套餐、短信发送、手机验证码登录)
文章目录新增套餐需求分析数据模型准备工作前端页面分析代码开发根据分类查询菜品功能实现功能测试保存套餐功能实现功能测试思维导图总结套餐分页查询需求分析前端页面分析代码开发基本信息查询问题分析功能完善功能测试思维导图总结删除套餐需求分析前端页面分析代码开发功能…...
OpenAI 发布GPT-4——全网抢先体验
OpenAI 发布GPT-4 最近 OpenAI 犹如开挂一般,上周才刚刚推出GPT-3.5-Turbo API,今天凌晨再次祭出GPT-4这个目前最先进的多模态预训练大模型。与上一代GPT3.5相比,GPT-4最大的飞跃是增加了识图能力,并且回答准确性也得到显著提高。…...

C++——多态
多态分为两类静态多态:函数重载和运算符重载属于静态多态,复用函数名动态多态:派生类和虚函数实现运行时多态静态多态和动态多态的区别:静态多态的函数地址早绑定——编译阶段确定函数地址动态多态的函数地址晚绑定——运行阶段确…...

javaSE系列之类与对象
javaSE系列之类与方法什么是类类的定义书写事项什么是实例化this引用this的注意事项对象的初始化构造方法封装的概念访问限定符封装扩展之包static成员static的特性static的初始化代码块注意事项内部类1.实例内部类💗 💗 博客:小怡同学💗 &am…...
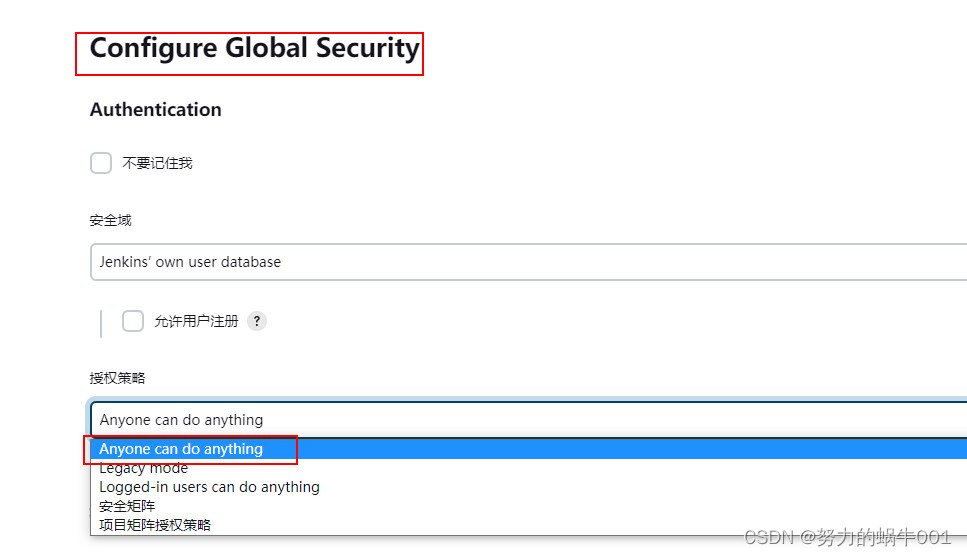
远程构建(命令、脚本构建)jenkins
在对应项目,开启远程构建开关添加API token系统设置调整用户权限获取crumbcurl调用构建 1、进入对应项目的设置页面:开启远程构建开关 2、 添加 API token:进入对应用户的设置页面 3、系统设置调整权限,如图 4、由于jenkins的安全…...
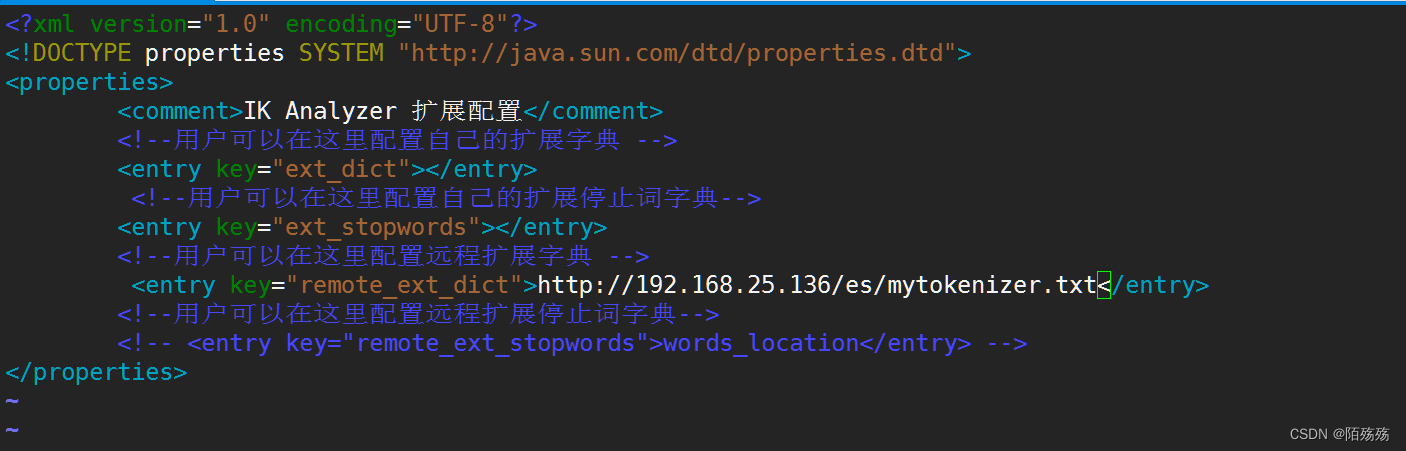
2023-03-15 ElasticSearch
ElasticSearch 1.Docker安装ElasticSearch 1.1. es及kibana下载 docker pull elasticsearch:7.4.2 docker pull kibana:7.4.2创建映射文件: mkdir -p /elasticsearch/configmkdir -p /elasticsearch/datamkdir -p /elasticsearch/plugins在config下执行 vim elasticsearch…...

指针和数组笔试题解析【下篇】
文章目录👁️6.指针笔试题👀6.1.试题(1)👀6.2.试题(2)👀6.3.试题(3)👀6.4.试题(4)👀6.5.试题(5&am…...
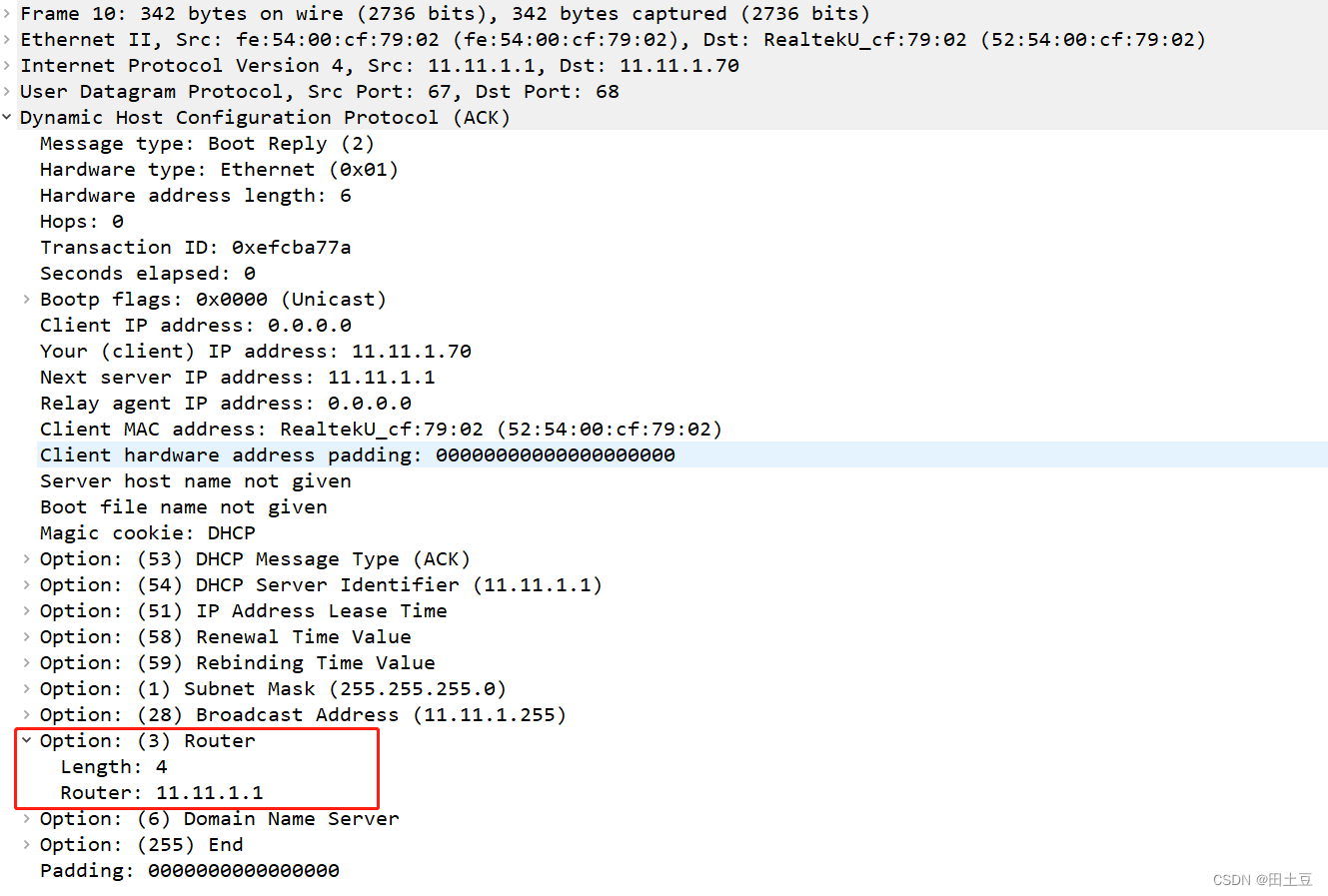
DHCP原理简析及交互实践
环境: os:centos7 dnsmasq:version 2.76 一. dhcp工作原理 首先补充几个dhcp相关的基本概念: 1、动态主机配置协议DHCP(Dynamic Host Configuration Protocol)是一种网络管理协议,用于集中对用…...
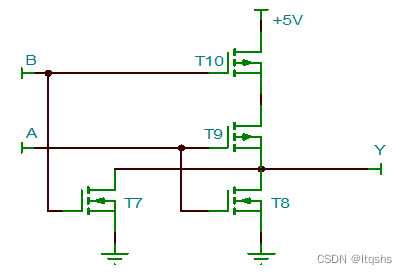
用二极管、三极管和MOS管搭建逻辑门电路
文章目录1. 二极管(1)二极管与门(2)二极管或门2. 三极管(1)三极管非门(2)三极管与门(3)三极管或门(4)三极管与非门(5&…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

大模型真的像人一样“思考”和“理解”吗?
Yann LeCun 新研究的核心探讨:大语言模型(LLM)的“理解”和“思考”方式与人类认知的根本差异。 核心问题:大模型真的像人一样“思考”和“理解”吗? 人类的思考方式: 你的大脑是个超级整理师。面对海量信…...

生信服务器 | 做生信为什么推荐使用Linux服务器?
原文链接:生信服务器 | 做生信为什么推荐使用Linux服务器? 一、 做生信为什么推荐使用服务器? 大家好,我是小杜。在做生信分析的同学,或是将接触学习生信分析的同学,<font style"color:rgb(53, 1…...
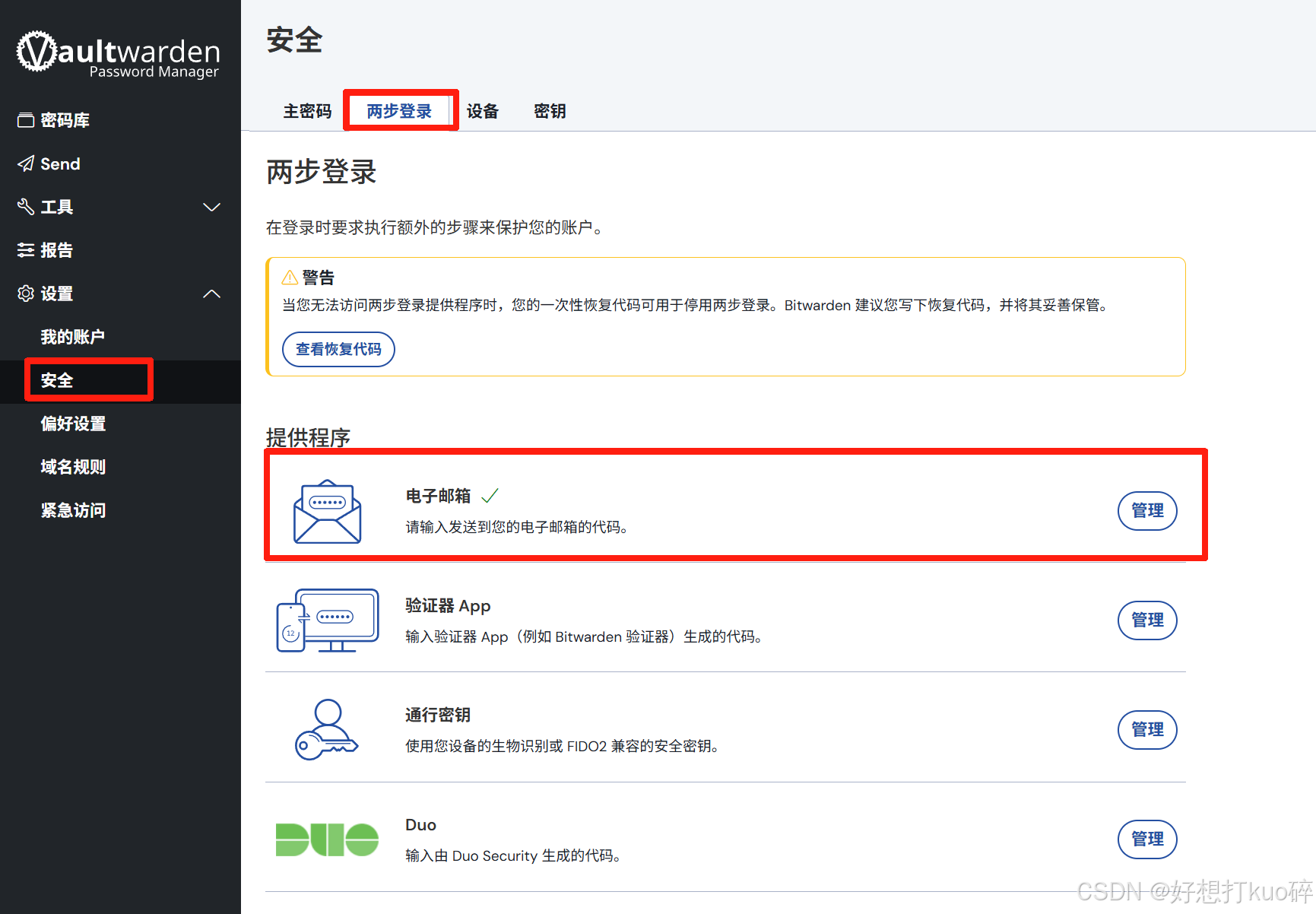
轻量安全的密码管理工具Vaultwarden
一、Vaultwarden概述 Vaultwarden主要作用是提供一个自托管的密码管理器服务。它是Bitwarden密码管理器的第三方轻量版,由国外开发者在Bitwarden的基础上,采用Rust语言重写而成。 (一)Vaultwarden镜像的作用及特点 轻量级与高性…...