数学系C++ 排序算法简述(八)
目录
排序
选择排序 O(n2)
不稳定:48429
归并排序 O(n log n) 稳定
插入排序 O(n2)
堆排序 O(n log n)
希尔排序 O(n log2 n)
图书馆排序 O(n log n)
冒泡排序 O(n2)
优化:
基数排序 O(n · k)
快速排序 O(n log n)【分治】 不稳定
桶排序 O(n + k)
计数排序 O(n + k)
鸽巢排序 O(n + D)
排序
什么是稳定排序算法:数据先后次序不变
选择排序 O(n2) 归并排序 O(n log n)插入排序 O(n2) 堆排序 O(n log n)希尔排序 O(n log2 n) 图书馆排序 O(n log n)冒泡排序 O(n2) 基数排序 O(n · k)快速排序 O(n log n) 桶排序 O(n + k)计数排序 O(n + k)鸽巢排序 O(n + D):

选择排序 O(n2)
► 先找出最小值,将其与第一个位置的元素进行交换
► 对剩余的数据重复以上过程,直至排序结束
不稳定:48429
归并排序 O(n log n) 稳定
归并:如果有两个分别有序的数组,可以用双指针合并成一个完全有序的数组
可以递归写
也可以从0开始
归并1-1 1-1 1-1 1-1
归并 2-2 2-2
归并 4-4
完成!
插入排序 O(n2)
假设前面 k 个元素已经按顺序排好了,在排第 k+1个元素时,将其插入到前面已排好的 k 个元素中,使得插入后得到的 k+1 个元素组成的序列仍按值有序。
堆排序 O(n log n)
希尔排序 O(n log2 n)
基本过程描述如下:
① 把序列按照某个增量(gap)分成几个子序列,对这几个子序列进行插入排序。
② 不断缩小增量,扩大每个子序列的元素数量,并对每个子序列进行插入排序。
③ 当增量为 1 时,子序列就是整个序列,而此时序列已经基本有序了,因此只需做少量的比较和移动就可以完成对整个序列的排序
出发点:插入排序在元素基本有序的情况下,效率很高。
gap:初始值设为 n/2,然后不断减半。

图书馆排序 O(n log n)
冒泡排序 O(n2)
► 走访需要排序的序列,比较相邻的两个元素,如果他们的顺序错误就把他们交换过来。
► 不断重复上述过程,直到没有元素需要交换
具体过程:
► 将第 1 个和第 2 个元素进行比较,如果前者大于后者,则交换两者 的位置,否则位置不变;然后将第 2 个元素与第 3 个元素进行比较, 如果前者大于后者,则交换两者的位置,否则位置不变;依此类推, 直到最后两个元素比较完毕为止。这就是第一轮冒泡过程,这个过程 结束后,最大的元素就“浮”到了最后一个位置上。
► 对前面 n-1 个元素进行第二轮冒泡排序,结束后,这 n-1 个元素中 的最大值就被安放在了第 n-1个位置上。
……执行n-1轮
优化:
简单优化:
如果在某轮冒泡过程中没有发生元素交换,这说明整个序列已经排好序了,这时就不用再进行后面的冒泡过程,可以直接结束程序
进一步优化:
假设有 100 个数组成的数组,仅前面10个无序,后面90个都已排好序且都大于前面10个数字,那么在第一轮冒泡过程后,最后发生交换的位置必定小于10,且这个位置之后的数据必定已经有序了,记录下这位置,第二轮遍历是只要到这个位置就可以了。记录每轮遍历最后发生交换的位置,下次遍历只需到此位置为止
基数排序 O(n · k)
先排个位,再排十位,再排百味(30次)
快速排序 O(n log n)【分治】 不稳定
快速排序采用的是分而治之思想:将原问题分解为若干个规模更小但结构与原问题相似的子问题,然后递归求解这些子问题,最后将这些子问题的解组合为原问题的解
1.以第一个元素为基准书,使得基准书左边只有比他小的,右边只有比他大的
2.然后对基准书两边的数组分别进行操作1
分治:分成相同的子问题,用递归求解;子问题相互独立
dp:子问题不一定相同,具有最优子结构;子问题相互依赖
桶排序 O(n + k)
计数排序 O(n + k)
鸽巢排序 O(n + D)
相关文章:

数学系C++ 排序算法简述(八)
目录 排序 选择排序 O(n2) 不稳定:48429 归并排序 O(n log n) 稳定 插入排序 O(n2) 堆排序 O(n log n) 希尔排序 O(n log2 n) 图书馆排序 O(n log n) 冒泡排序 O(n2) 优化: 基数排序 O(n k) 快速排序 O(n log n)【分治】 不稳定 桶排序 O(n…...

记一下blender曲线阵列
先说一下如何正常使用这个 这一次我是用来贴瓷砖 随便创建一个mesh 然后添加一个阵列修改器,然后再给他添加一个curve修改器,使用constant offset去偏移他 这里有个小细节 我第一次创建的curve 我选取之后,死活无法沿着曲线阵列ÿ…...
Windows电脑安装Python结合内网穿透轻松搭建可公网访问私有网盘
文章目录 前言1.本地文件服务器搭建1.1.Python的安装和设置1.2.cpolar的安装和注册 2.本地文件服务器的发布2.1.Cpolar云端设置2.2.Cpolar本地设置 3.公网访问测试4.结语 前言 本文主要介绍如何在Windows系统电脑上使用python这样的简单程序语言,在自己的电脑上搭建…...

react hooks antd 父组件取子组件form表单的值
在React中,父组件可以使用ref来访问子组件的方法或属性。子组件包含一个表单, 使用forwardRef、useImperativeHandle:forwardRef允许组件使用ref将 DOM 节点暴露给父组件,使用useImperativeHandle暴露方法给父组件。 子组件&#…...

【ARMv8/v9 GIC 系列 1.7 -- GIC PPI | SPI | SGI | LPI 中断使能配置概述】
请阅读【ARM GICv3/v4 实战学习 】 文章目录 GIC 各种中断使能配置PPIs(每个处理器私有中断)SPIs(共享外设中断)SGIs(软件生成的中断)LPIs(局部中断)GIC 各种中断使能配置 在ARM GICv3和GICv4架构中,不同类型的中断(如PPIs、SPIs、SGIs和LPIs)可以通过不同的方式进…...

大数据如何推动工业数字化发展?
随着工业领域的深刻变革,数字化成为了驱动行业前行的核心力量。在这一转变中,大数据扮演着不可或缺的角色。它不仅为企业提供了洞察市场趋势、消费者行为等关键信息的窗口,还为企业优化生产流程、提升产品质量以及推动创新提供了强有力的支持…...

计算机网络浅谈—什么是 OSI 模型?
开放系统通信(OSI)模型是一个代表网络通信工作方式的概念模型。 思维导图 什么是 OSI 模型? 开放系统互连 (OSI) 模型是由国际标准化组织创建的概念模型,支持各种通信系统使用标准协议进行通信。简单而言,OSI 为保证…...

浪潮服务器内存物理插槽位置
浪潮服务器内存物理插槽位置 如下图所示...

windows node降级到指定版本
要在Windows上将Node.js降级到指定版本,你可以使用nvm(Node Version Manager)来管理和切换不同的Node.js版本。以下是使用nvm降级Node.js的步骤: 如果尚未安装nvm,请访问https://github.com/coreybutler/nvm-windows …...
EXSI 实用指南 2024 -编译环境 Mac OS 安装篇(一)
1. 引言 在现代虚拟化技术的快速发展中,VMware ESXi 作为领先的虚拟化平台,凭借其高性能、稳定性和丰富的功能,广泛应用于企业和个人用户。ESXi 能有效地提高硬件资源利用率,并简化 IT 基础设施的管理。然而,如何在 V…...
断电的固态硬盘数据能放多久?
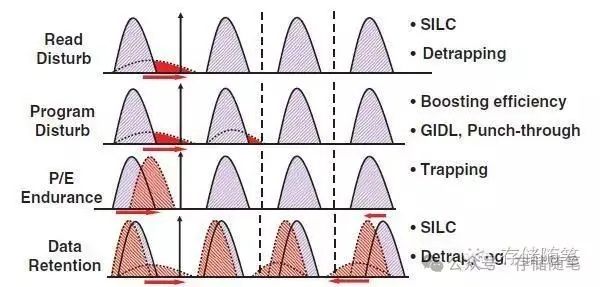
近日收到一个网友的提问,在这里粗浅表达一下见解: “网传固态硬盘断电后数据只能放一年,一年之后就会损坏。但是我有一个固态硬盘已经放了五六年了(上次通电还是在2018年左右,我读初中的时候),…...

Neo4j安装
下载地址:Neo4j Deployment Center - Graph Database & Analytics 1.安装jdk,Neo4j 3.0需要jdk8,2.3.0之前的版本建议jdk7。Neo4j最新版本5.21.2,对应jdk版本17 2.将下载的zip文件解压到合适路径。 3.设置环境变量NEO4J_H…...

基于Java+SpringMvc+Vue技术的就医管理系统设计与实现系统(源码+LW+部署讲解)
目录 界面展示 第六章 部分代码实现 6.1 Spring boot 配置代码 6.2 用户管理及登录登出代码 6.3 Md5 加密算法代码 6.4 部分数据库代码 六、论文参考: 七、其他案例: 系统介绍: 就医管理系统,也称为医院管理系统&#…...

Transformer学习过程中常见的问题与解决方案 - Transformer教程
在机器学习领域,Transformer模型已经成为了处理自然语言处理(NLP)任务的主流工具。然而,在学习和使用Transformer的过程中,很多人会遇到各种各样的问题。今天我们就来聊一聊Transformer学习过程中常见的问题以及对应的…...
Linux进程间通信:匿名管道 命名管道
Linux进程间通信:匿名管道 &命名管道 一、进程间通信目的二、什么是管道三、匿名管道创建3.1 系统调用原型3.2 匿名管道创建 四、内核创建匿名管道过程五、匿名管道性质5.1 匿名管道的4种特殊情况5.2 匿名管道的5种特性5.3 测试源代码 六、命名管道6.1 创建命名…...
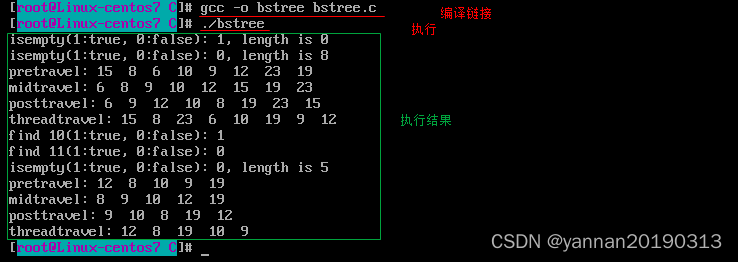
【数据结构】(C语言):二叉搜索树(不使用递归)
二叉搜索树: 非线性的,树是层级结构。基本单位是节点,每个节点最多2个子节点。有序。每个节点,其左子节点都比它小,其右子节点都比它大。每个子树都是一个二叉搜索树。每个节点及其所有子节点形成子树。可以是空树。 …...

Fastapi在docekr中进行部署之后,uvicorn占用的CPU非常高
前一段接点小活,做点开发,顺便学了学FASTAPI框架,对比flask据说能好那么一些,至少并发什么的不用研究其他的asgi什么的,毕竟不是专业开发,能少研究一个东西就省了很多的事。 但是部署的过程中突然之间在do…...

Pandas数据可视化宝典:解锁图形绘制与样式自定义的奥秘
Pandas数据可视化宝典:解锁图形绘制与样式自定义的奥秘 引言 数据可视化是将数据以图形或图像的形式展示出来,使复杂的数据更容易被人类理解和分析。在数据分析、商业智能、科学研究等领域,数据可视化都扮演着至关重要的角色。Pandas作为一…...

2024前端面试真题【JS篇】
DOM DOM:文本对象模型,是HTML和XML文档的编程接口。提供了对文档的结构化的表述,并定义可一种方式可以使从程序中对该结构进行访问,从而改变文档的结构、样式和内容。 DOM操作 创建节点:document.createElement()、do…...

axios使用sm2加密数据后请求参数多了双引号解决方法
axios使用sm2加密数据后请求参数多了双引号解决 背景问题描述解决过程 背景 因项目安全要求,需对传给后端的入参加密,将请求参数加密后再传给后端 前期将axios降低到1.6.7后解决了问题,但最近axios有漏洞,安全要求对版本升级&…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...
