π-Day快乐:Python可视化π
π-Day快乐:Python可视化π
今天是3.14,正好是圆周率 π\piπ 的前3位,因此数学界将这一天定为π\bold{\pi}π day。
π\piπ 可能是最著名的无理数了,人类对 π\piπ 的研究从未停止。目前人类借助计算机已经计算到 π\piπ 小数点后31.4万亿位了!这个记录是由来自Google的日本女程序员岩尾遥创造的。据说该计算程序在25台虚拟机上运行了121天,涉及170TB的数据,最终获得精确到 π\piπ 小数点后31.4万亿位的成绩。
计算 π\piπ 的精度也是衡量计算机算力的一种方法,该方法始于冯·诺依曼。直到今天依然有很多数学家在孜孜不倦地研究 π\piπ 的各种性质,甚至有人认为 π\piπ 小数位蕴含着宇宙的终极奥秘。今天我们用Python将 π\piπ 可视化,看看会诞生什么惊人的图案。

文章目录
- 思路
- 点图
- 线段图
- 结论
思路
首先,我从网上下载了 π\piπ 小数点后100万位,保存在文本文件中。每50位一行,数据张这个样子:
14159265358979323846264338327950288419716939937510
58209749445923078164062862089986280348253421170679
82148086513282306647093844609550582231725359408128
48111745028410270193852110555964462294895493038196
44288109756659334461284756482337867831652712019091
45648566923460348610454326648213393607260249141273
72458700660631558817488152092096282925409171536436
然后我会用一定规则来可视化[0-9]这10个数字。目前想到的有两种:
- 点图 将[0-9]10个数字,每个数字赋一个颜色,然后一次绘制圆点。

- 线段图 [0-9]10个数字每个数字赋一个颜色和角度,绘制收尾相接的线段。

点图
点图的绘制相对简单,首先定义颜色:
# 圆点边线颜色
color = ['gold', 'goldenrod', 'red', 'firebrick', 'mediumvioletred', 'darkorchid', 'royalblue', 'lightseagreen', 'mediumseagreen', 'olivedrab']
# 圆点填充颜色
color_fill = ['khaki', 'moccasin', 'lightcoral', 'lightsalmon', 'orchid', 'mediumpurple', 'skyblue', 'aquamarine', 'lightgreen', 'palegreen']
数字[0-9]当作颜色的下标索引获取颜色,绘制单个圆点的代码如下:
def draw_dot(n: int, c: int):""" 绘制圆点:param n: 小数位数值:param c: 第几位:return: None"""t.color(color_fill[n])t.begin_fill()t.circle(10)t.end_fill()t.color(color[n])t.circle(10)pos = t.pos()
绘制完一个圆点后,turtle移动到下一个位置,这里我设置为每40位换一行:
def move(c: int):""" 移动到下一位置:param c: 小数点后第几位:return: None"""pos = t.pos()t.penup()if c % 40 == 0: #每40位换一行t.goto(-600, pos[1] - 30)else:t.goto(pos[0] + 30, pos[1])t.pendown()
最后我们只要读取 π\piπ 的小数位,循环绘制圆点即可:
import turtleturtle.setup(1.0, 1.0)
t = turtle.Turtle()
t.hideturtle()
t.pensize(2)
t.penup()
t.goto(-600, 400)
t.pendown()
t.speed(0)# 绘制整数位3
count = 1
num = 3
draw_dot(num, count)
move(count)# 循环绘制小数位
with open('圆周率前100万位.txt') as f:for i in range(28): # 绘制28*50=1400位word = f.readline().strip()for a in word:num = int(a)count += 1draw_dot(num, count)move(count)f.close()turtle.done()
最终效果如下图:

线段图
有了点图的基础,线段图的绘制相对简单。直接上代码:
import turtleturtle.setup(1.0, 1.0)
t = turtle.Turtle()
t.hideturtle()
t.pensize(2)
t.pendown()
t.left(90)
t.speed(0)
color = ['gold', 'goldenrod', 'red', 'firebrick', 'mediumvioletred', 'darkorchid', 'royalblue', 'lightseagreen', 'mediumseagreen', 'greenyellow']# 绘制整数位3
last_num = 3
t.color(color[last_num])
t.right(last_num * 36)
t.forward(40)# 循环绘制小数位
with open('圆周率前100万位.txt') as f:for i in range(100):word = f.readline().strip()for a in word:current_num = int(a)t.color(color[current_num])angle = (current_num - last_num) * 36t.right(angle)t.forward(20)last_num = current_numf.close()turtle.done()最终效果:

结论
怎么样?很神奇吧?如果你有更好的可视化思路,欢迎留言评论交流。
最后,祝大家 π\piπ Day快乐!
相关文章:

π-Day快乐:Python可视化π
π-Day快乐:Python可视化π 今天是3.14,正好是圆周率 π\piπ 的前3位,因此数学界将这一天定为π\bold{\pi}π day。 π\piπ 可能是最著名的无理数了,人类对 π\piπ 的研究从未停止。目前人类借助计算机已经计算到 π\piπ 小数…...
【论文速递】ACM MM 2022 - 基于统一对比学习框架的新闻多媒体事件抽取
【论文速递】ACM MM 2022 - 基于统一对比学习框架的新闻多媒体事件抽取 【论文原文】:Multimedia Event Extraction From News With a Unified Contrastive Learning Framework 【作者信息】:Liu, Jian and Chen, Yufeng and Xu, Jinan 论文ÿ…...

数据库分库分表
一、为什么要分库分表 如果一个网站业务快速发展,那这个网站流量也会增加,数据的压力也会随之而来,比如电商系统来说双十一大促对订单数据压力很大,Tps十几万并发量,如果传统的架构(一主多从),主库容量肯定无法满足这么高的Tps,业务越来越大,单表数据超出了数据库支持…...

【C缺陷与陷阱】----语义“陷阱”
💯💯💯 本篇处理的是有关语义误解的问题:即程序员的本意是希望表示某种事物,而实际表示的却是另外一种事物。在本篇我们假定程序员对词法细节和语法细节的理解没有问题,因此着重讨论语义细节。导言…...

JavaWeb--VUE
VUE1 概述2 快速入门3 Vue 指令3.1 v-bind & v-model 指令3.2 v-on 指令3.3 条件判断指令3.4 v-for 指令4 生命周期5 案例5.1 需求5.2 查询所有功能5.3 添加功能目标 能够使用VUE中常用指令和插值表达式能够使用VUE生命周期函数 mounted 1 概述 接下来我们学习一款前端的框…...

2分钟彻底搞懂“高内聚,低耦合”
💗推荐阅读文章💗 🌸JavaSE系列🌸👉1️⃣《JavaSE系列教程》🌺MySQL系列🌺👉2️⃣《MySQL系列教程》🍀JavaWeb系列🍀👉3️⃣《JavaWeb系列教程》…...

网络编程UDP TCP
定义:关注底层数据的传输 区分网页编程:关注上层应用 端口号:区分软件 2个字节 0~65535表示端口号 同一协议下端口号不能冲突 8000以下称为预留端口号,建议之间设置端口号为8000以上 常见的端口号: 80:http 8080:tomcat 3306:mysql 1521:oracle InetSocketAddress:此类实现IP套…...
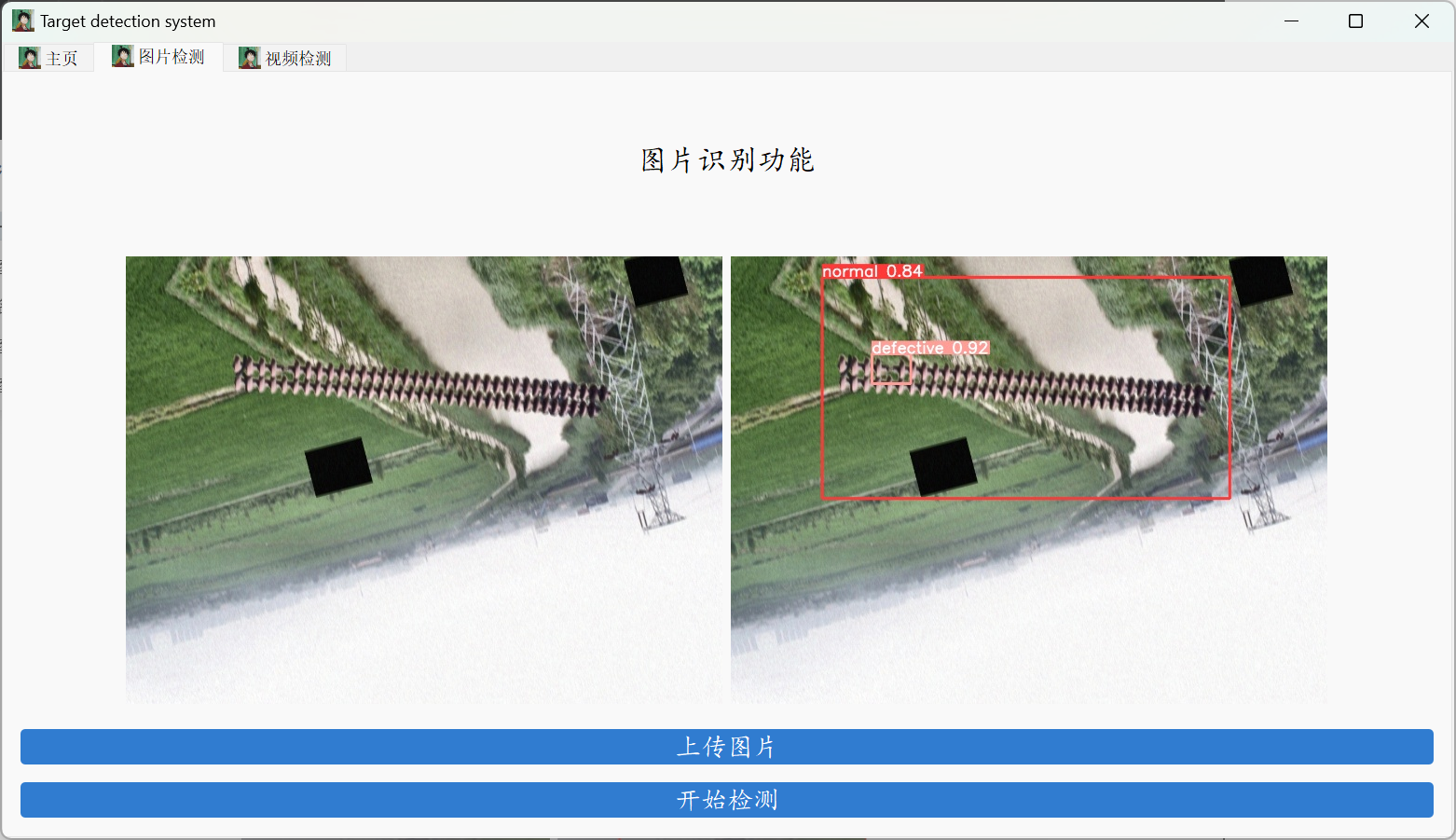
【2023-Pytorch-检测教程】手把手教你使用YOLOV5做电线绝缘子缺陷检测
随着社会和经济的持续发展,电力系统的投资与建设也日益加速。在电力系统中,输电线路作为电能传输的载体,是最为关键的环节之一。而绝缘子作为输电环节中的重要设备,在支撑固定导线,保障绝缘距离的方面有着重要作用。大…...
)
交叉编译(NDK)
文章目录前言Android-NDK使用NDK目录结构主流的Android NDK交叉编译前言 交叉编译是指在一种计算机体系结构上编译和构建应用程序,但是生成的可执行文件和库是针对另一种不同的体系结构,比如ARM、MIPS、PowerPC、x86 等。 常见的交叉编译工具集&#x…...

【数据库】MySQL 解读事务的意义及原则
目录 1.事务的概念 2.为什么要用事物 3.使用 4.事务的原则(ACID) 4.1原子性(Atomicity) 4.2一致性(Consistency) 4.3持久性(Durability) 4.4隔离性(Isolation…...
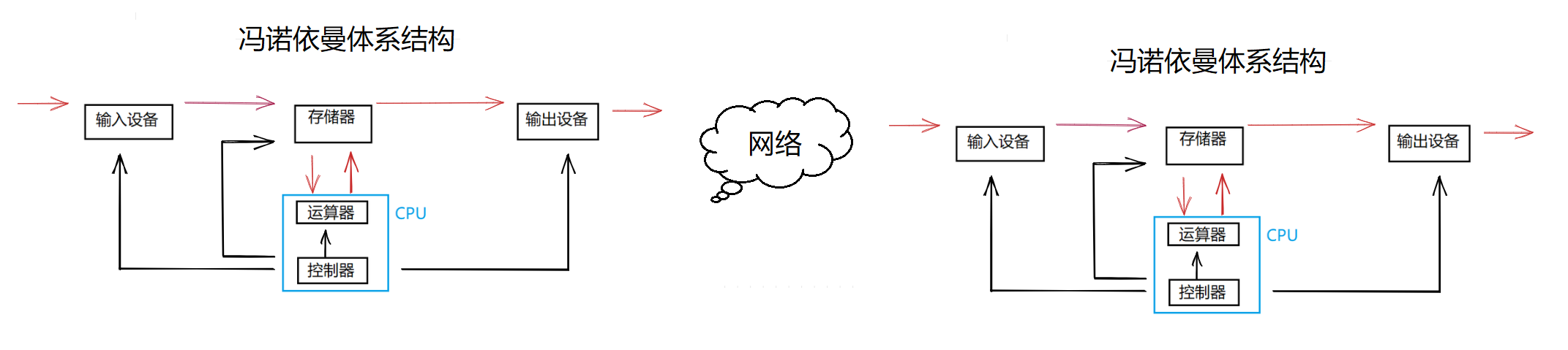
【Linux】冯诺依曼体系结构
冯诺依曼体系结构一、计算机结构体系来源二、冯诺依曼体系结构三、冯诺依曼体系结构中的数据流动一、计算机结构体系来源 研制电子计算机的想法产生于第二次世界大战期间,主要用来进行弹道计算,在"时间就是胜利"的战争年代,迫切需…...

【小白】git是什么?gitee和git和github的关系?
gitee问题一、git是什么?gitee和git和github的关系?问题二、能不能通俗易懂的说?问题一、git是什么?gitee和git和github的关系? Git是一种版本控制系统,用于管理文件的版本、记录文件的修改历史以及协同开…...

UDS 14229 -1 刷写34,36,37服务,标准加Trace讲解,没理由搞不明白
🍅 我是蚂蚁小兵,专注于车载诊断领域,尤其擅长于对CANoe工具的使用🍅 寻找组织 ,答疑解惑,摸鱼聊天,博客源码,点击加入👉【相亲相爱一家人】🍅 玩转CANoe&…...

【Android -- 软技能】聊聊程序员的软技能
什么是软技能? 所谓软技能,就是相对于「硬技能」而言的技能,对于程序员来说,「硬技能」就是计算机专业技术能力,软技能则是专业之外的所有技能,包括职业规划能力、处理人际关系能力、专业态度、做事的方式…...

【Java学习笔记】27.Java 抽象类
Java 抽象类 在面向对象的概念中,所有的对象都是通过类来描绘的,但是反过来,并不是所有的类都是用来描绘对象的,如果一个类中没有包含足够的信息来描绘一个具体的对象,这样的类就是抽象类。 抽象类除了不能实例化对象…...

Vite4 + Vue3 + vue-router4 动态路由
动态路由,基本上每一个项目都能接触到这个东西,通俗一点就是我们的菜单是根据后端接口返回的数据进行动态生成的。表面上是对菜单的一个展现处理,其实内部就是对router的一个数据处理。这样就可以根据角色权限或者一些业务上的需求࿰…...
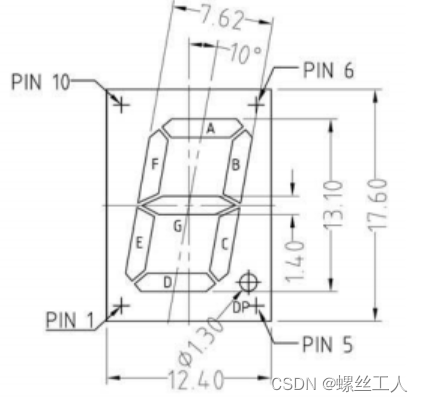
MS(mbed l432KC)-->速通9个lab详细解析[5]
Exercise5 这次实验我们将正式接触到一个相对来说有点意思并且有点牌面的传感器了----->数码管。数码管是我们生活中非常常见的一种传感器,比如计时器,秒表,以及数字显示大屏幕,其实原理都跟数码管差不多。如果是没有单片机基础的同学,突然一下接触到相对来说比较常见…...
XXE漏洞复现
目录XML基础概念XML数据格式DTD基础定义DTD作用分类DTD实体实体的分类DTD元素XXE漏洞介绍实操如何探测xxe漏洞XML基础 概念 什么是XML 是一种可扩展标记语言 (Extensible Markup Language, XML) ,标准通用标记语言的子集,可以用来标记数据、定义数据类型…...

初识C++需要了解的一些东西(2)
😁关注博主:翻斗花园第一代码手牛爷爷 😃Gitee仓库:牛爷爷爱写代码 目录🌍内联函数🌕内联函数概念🌖内联函数特性🌓auto关键字(C11)🌞类型别名⭐️auto简介☀️auto的使…...
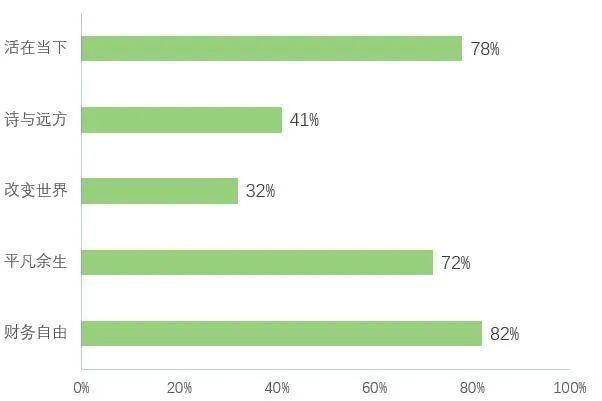
全国程序员薪酬大曝光!看完我酸了····
2023年,随着互联网产业的蓬勃发展,程序员作为一个自带“高薪多金”标签的热门群体,被越来越多的人所关注。在过去充满未知的一年中,他们的职场现状发生了一定的改变。那么,程序员岗位的整体薪资水平、婚恋现状、职业方…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...
