算法学习笔记(8.4)-完全背包问题
目录
Question:
图例:
动态规划思路
2 代码实现:
3 空间优化:
代码实现:
下面是0-1背包和完全背包具体的例题:
代码实现:
图例:
空间优化代码示例
Question:
给定n个物品,第i个物品的重量为wgt[i-1],价值为val[i-1],和一个容量为cap的背包。每个物品可以重复选取,问在限定背包容量的情况下能放入物品的最大价值。
图例:

-
动态规划思路
完全背包问题和0-1背包问题非常相似,区别仅在于不限制物品的选择次数。
- 在0-1背包问题中,每种物品只有一个,因此将物品i放入到被曝后,只能从前i-1个物品选择。
- 在完全背包问题中,每种物品的数量都是无限的,因此将物品i放入到背包后,仍可以从前i个物品中选择。
在完全背包问题的规定下,状态[i,c]的变化分为以下两种情况。
- 不放入物品i:与0-1背包问题相同转移至[i-1,c]。
- 放入物品i:与0-1背包问题不同,转移至[i,c-wgt[i-1]]。
从而转移状态方程为:
dp[i,c] = max(dp[i-1,c],dp[i,c-wgt[i-1]]+val[i-1])
2 代码实现:
# python 代码示例
def unbound_knap_sack_dp(wgt, val, cap) :n = len(wgt)dp = [ [0] * (cap + 1) for _ in range(n + 1)]for i in range(1, n + 1) :for j in range(1, cap + 1) :if wgt[i - 1] > c :dp[i][c] = dp[i - 1][c]else :dp[i][c] = max(dp[i - 1][c], dp[i][c - wgt[i - 1]] + val[i - 1])return dp[n][cap]// c++ 代码示例int unboundKnapSackDP(vector<int> &wgt, vector<int> &val, int cap)
{int n = wgt.size() ;vector<vector<int>> dp(n + 1, vector<int>(cap + 1, 0)) ;for (int i = 1 ; i <= n ; i++){for (int j = 1 ; j <= cap ; j++){if (wgt[i - 1] > c){dp[i][c] = dp[i - 1][c] ;}else{dp[i][c] = max(dp[i - 1][c], dp[i][c - wgt[i - 1]] + val[i - 1) ;}}}return dp[n][cap] ;
}3 空间优化:
由于当前状态是从左边和上边的状态转移而来,因此空间优化后应该对dp表中的每一行进行正序遍历。
图例所示:

代码实现:
# python 代码示例def unbound_knap_sack_dp_comp(wgt, val, cap) :n = len(wgt)dp = [0] * (cap + 1)for i in range(1, n + 1) :for j in range(1, cap + 1) :if wgt[i - 1] > c :dp[c] = dp[c]else :dp[c] = max(dp[c], dp[c - wgt[i - 1]] + val[i - 1]) return dp[cap] ;// c++ 代码示例int unboundKnapSackDPComp(vector<int> &wgt, vector<int> &val, int cap)
{int n = wgt.size() ;vector<int> dp(cap + 1, 0) ;for (int i = 1 ; i <= n ; i ++){for (int j = 1 ; j <= cap ; j++){if (wgt[i - 1] > c){dp[c] = dp[c] ;}else{dp[c] = max(dp[c], dp[c - wgt[i - 1]] + val[i - 1]) ;}}}return dp[c] ;
}下面是0-1背包和完全背包具体的例题:
零钱兑换问题:给定n中硬币,第i种硬币的面值为coins[i-1],目标金额为amt,每种硬币可以重复选取,问能够凑出目标金额的最少硬币数。如果无法凑出目标金额,则返回-1。
图例:

动态规划的思路:
零钱兑换可以看作是完全背包的一种特殊情况,两者具有以下联系和不同点。
- 两道题目可以相互转化,“物品“对应”硬币“、”物品重量“对应”硬币面值“、”背包容量“对应”目标金额“。
- 优化目标相反,完全背包问题是要最大化物品价值,零钱兑换问题是要最小化硬币数量。
- 完全背包问题是求“不超过“背包容量下的解,零钱兑换是求”恰好“凑到目标金额的解。
第一步:思考每轮的决策,定义状态,从而得到dp表
状态[i,a]对应的子问题为:前i种硬币能够凑出金额a的最少硬币数量,记作dp[i,a]。
二维dp表的尺寸为(n+1)*(amt+1).
第二步:找出最优子结构,进而推导出状态转移方程
本题与完全背包问题的转移状态方程存在以下两点差异。
- 本题要求最小值,因此需将运算符max()更改为min()。
- 优化主体是硬币数量而非商品的价值,因此在选中硬币时需执行+1即可。
dp[i,a] = min(dp[i-1,a],dp[i,a-coins[i-1]]+1)
第三步:确定边界和状态转移顺序
当目标金额为0时,凑出它的最小硬币数量为0,即首列所有dp[i,0]都等于0。
当无硬币时,无法凑出任意>0的目标金额,即使无效解。为使状态转移方程中的min()函数能够识别并过滤无效解,我们使用+∞来表示他们,即令首行所有dp[0,a]都等于+∞。
代码实现:
def coin_change_dp(coins, amt) :n = len(coins)dp = [ [0] * (amt + 1) for _ in range(n + 1)]for j in range(1, amt + 1) :dp[0][j] = inffor i in range(1, n + 1) :dp[i][0] = 0for i in range(1, n + 1) :for j in range(1, cap + 1) :if coins[i - 1] > j :dp[i][j] = dp[i - 1][j]else :dp[i][j] = max(dp[i - 1][j], dp[i][j - coins[i - 1]] + 1)return dp[n][amt] if dp[n][amt] != inf else -1int coinsChangeDP(vector<int> &coins, int amt)
{int n = coins.size() ;vector<vector<int>> dp(n + 1, vector<int>(amt + 1, 0)) ;for (int j = 1 ; j <= amt ; j++) {dp[0][j] = INT_MAX ;}for (int i = 1 ; i <= n ; i++){dp[i][0] = 0 ;}for (int i = 1 ; i <= n ; i++){for (int j = 1 ; j <= amt ; j++){if (coins[i - 1] > j){dp[i][j] = dp[i - 1][j] ;}else{dp[i][j] = min(dp[i - 1][j], dp[i][j - coins[i - 1]] + 1) ;}}}return dp[n][amt] != INT_MAX ? dp[n][amt] : -1 ;}图例:

空间优化代码示例:
# python 代码示例def coins_change_dp_comp(coins, amt) :n = len(coins)dp = [inf] * (amt + 1)for i in range(1, n + 1) :for j in range(1, cap + 1) :if (coins[i - 1] > j) :dp[j] = dp[j]else :dp[j] = min(dp[j], dp[j - coins[i - 1]] + 1)return dp[amt] if dp[amt] != inf else -1// c++ 代码示例
int coinsChangeDPComp(vector<int> &coins, int amt)
{int n = coins.size() ;vector<int> dp(cap + 1, INT_MAX) ;for (int i = 1 ; i <= n ; i++){for (int j = 1 ; j <= amt ; j++){if (coins[i - 1] > j){dp[j] = dp[j] ;}else{dp[j] = min([j], [j - coins[i - 1]] + 1) ;}}}return dp[amt] != INT_MAX ? dp[amt] : -1 ;}相关文章:

算法学习笔记(8.4)-完全背包问题
目录 Question: 图例: 动态规划思路 2 代码实现: 3 空间优化: 代码实现: 下面是0-1背包和完全背包具体的例题: 代码实现: 图例: 空间优化代码示例 Question: 给定n个物品…...
陈述)
C++catch (...)陈述
catch (...)陈述 例外处理可以有多个catch,如果catch后的小括弧里面放...,就表示不限型态种类的任何例外。 举例如下 #include <iostream>int main() {int i -1;try {if (i > 0) {throw 0;}throw 2.0;}catch (const int e) {std::cout <…...

Redis实践
Redis实践 使用复杂度高的命令 如果在使用Redis时,发现访问延迟突然增大,如何进行排查? 首先,第一步,建议你去查看一下Redis的慢日志。Redis提供了慢日志命令的统计功能,我们通过以下设置,就…...

【Lora模型推荐】Stable Diffusion创作具有玉石翡翠质感的图标设计
站长素材AI教程是站长之家旗下AI绘图教程平台 海量AI免费教程,每日更新干货内容 想要深入学习更多AI绘图教程,请访问站长素材AI教程网: AI教程_深度学习入门指南 - 站长素材 (chinaz.com) logo版权归各公司所有!本笔记仅供AIGC…...

vscode 远程开发
目录 vscode 远程连接 选择 Python 环境 vscode 远程连接 按 CtrlShiftP 打开命令面板。输入并选择 Remote-SSH: Open SSH Configuration File...。选择 ~/.ssh/config 文件(如果有多个选项)。在打开的文件中添加或修改你的 SSH 配置。 这个可以右键…...
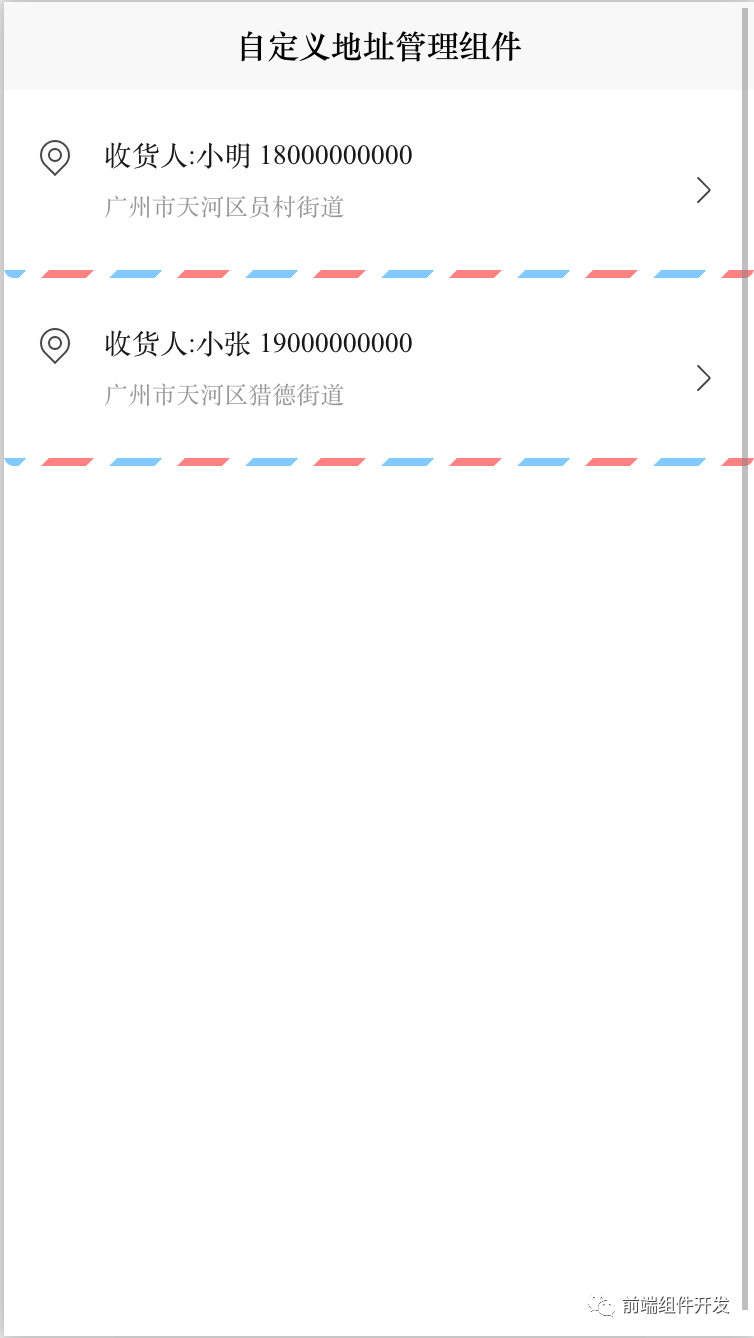
前端Vue组件化实践:打造灵活可维护的地址管理组件
随着前端技术的不断演进,复杂度和开发难度也随之上升。传统的一体化开发模式使得每次小小的修改或功能增加都可能牵一发而动全身,严重影响了开发效率和维护成本。组件化开发作为一种解决方案,通过模块化、独立化的开发方式,实现了…...

虚幻引擎ue5游戏运行界面白茫茫一片,怎么处理
根剧下图顺序即可调节游戏运行界面光照问题: 在大纲里找到post,然后选中它,找到Exposure 把最低亮度和最高亮度的0改为1即可...

《代理选择与反爬虫策略探究:如何优化网络爬虫效率与稳定性》
代理IP如何选以及常见反爬策略 为什么需要代理? 因为有的网站会封IP,用户如果没有登录,那IP就是身份标识,如果网站发现用户行为异常就非常可能封IP 什么是代理IP 就是让一个人帮你转交请求,帮你转交的人对面不熟&a…...

Kotlin Flow 防抖 节流
防抖和节流是针对响应跟不上触发频率这类问题的两种解决方案。 一:防抖(debounce)的概念: 防抖是指当持续触发事件时,一定时间段内没有再触发事件,事件处理函数才会执行一次, 如果设定时间到来之前&#x…...

Android Studio下载与安装
Android Studio下载与安装_android studio下载安装-CSDN博客...

【LC刷题】DAY24:122 55 45 1005
122. 买卖股票的最佳时机 II class Solution { public:int maxProfit(vector<int>& prices) {int result 0;for(int i 1; i < prices.size(); i ){result max(prices[i] - prices[ i - 1], 0);}return result;} };55. 跳跃游戏 link class Solution { public…...

从零开始的python学习生活2
接上封装 class Phone:__volt0.5def __keepsinglecore(self):print("让cpu以单核运行")def if5G(self):if self.__volt>1:print("5G通话已开启")else:self.__keepsinglecore()print("电量不足,无法使用5G通话,已经设置为单…...

【并发编程】进程 线程 协程
进程(Process)、线程(Thread)和协程(Coroutine)构成了计算机科学中实现任务并发执行的三种核心抽象机制。通常,为了提高程序的执行效率,开发者会根据应用场景和性能需求,…...

Vue的生命周期函数有哪些?详细说明
Vue.js 的生命周期函数包括以下几个阶段,每个阶段都有相应的钩子函数可以用来在特定时机执行自定义的逻辑。这些生命周期钩子函数使得我们可以在组件的不同阶段进行操作,从而管理组件的状态和行为。 1. beforeCreate: - 描述:…...

大语言模型应用--AI工程化落地
文章目录 大语言模型概述什么是大语言模型什么是机器学习什么是深度学习 理解大语言模型历史沿革关键 AIGC系统AI工程化项目的落地落地的方法Prompt工程(第一阶段)RAG检索(第二阶段)训练特定功能模型(第三阶段…...

我会什么开发技能
java我会什么? 一、并发编程 1、并发编程:jdk中的courren包只能够类实现(seamplore,CountDownLaunch,Pharse,CycliBarrier,CompletableFuture),AQS的原理,线…...

Run LoongArch64 Alpine VM on x86_64
一、Build from source(build on x86_64) Obtain the latest libvirt, virt-manager, and qemu source code, compile and install them. 1.1 Build libvirt from source sudo apt-get update sudo apt-get install augeas-tools bash-completion debhelper-compat dh-apparm…...

4层负载均衡和7层负载均衡
四层负载均衡(Layer 4 Load Balancing)指的是在网络传输层(TCP/IP模型中的第四层)进行负载均衡的技术。四层负载均衡通常使用IP地址、端口号和协议等信息来将网络流量分配到多个服务器上。它主要关心网络层的信息,不涉…...
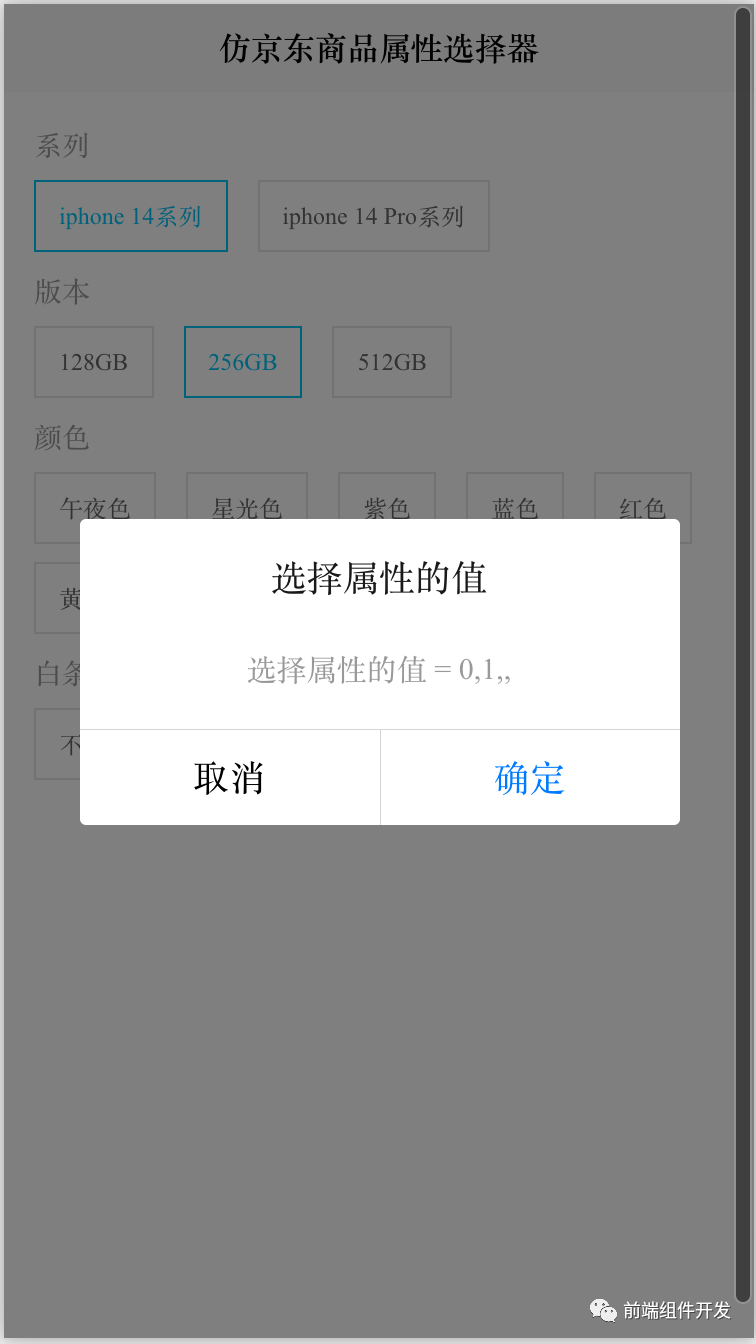
前端Vue组件化实践:打造仿京东天猫商品属性选择器组件
在前端开发领域,随着业务需求的日益复杂和技术的不断进步,传统的整体式应用开发模式已逐渐显得捉襟见肘。面对日益庞大的系统,每次微小的功能修改或增加都可能导致整个逻辑结构的重构,形成牵一发而动全身的困境。为了解决这一问题…...

智慧城市3d数据可视化系统提升信息汇报的时效和精准度
在信息大爆炸的时代,数据的力量无可估量。而如何将这些数据以直观、高效的方式呈现出来,成为了一个亟待解决的问题。为此,我们推出了全新的3D可视化数据大屏系统,让数据“跃然屏上”,助力您洞察先机,决胜千…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

简单介绍C++中 string与wstring
在C中,string和wstring是两种用于处理不同字符编码的字符串类型,分别基于char和wchar_t字符类型。以下是它们的详细说明和对比: 1. 基础定义 string 类型:std::string 字符类型:char(通常为8位)…...

EEG-fNIRS联合成像在跨频率耦合研究中的创新应用
摘要 神经影像技术对医学科学产生了深远的影响,推动了许多神经系统疾病研究的进展并改善了其诊断方法。在此背景下,基于神经血管耦合现象的多模态神经影像方法,通过融合各自优势来提供有关大脑皮层神经活动的互补信息。在这里,本研…...
