当前位置： 首页 > news >正文

2、ASPX、.NAT（环境/框架）安全

news 2025/10/31 20:45:07

ASPX、.NAT（环境/框架）安全

源自小迪安全b站公开课

1、搭建组合：

  • Windows
  • IIS
  • aspx
  • sqlserver

.NAT基于windows

C++开发的框架/环境

对抗Java

xx.dll <=> xx.jar

关键源码封装在dll文件内。

2、.NAT配置调试-信息泄露

功能点：
在这里插入图片描述

关闭customError：

泄露版本信息，部分路径
在这里插入图片描述

开启customError：

在这里插入图片描述

3、.NAT源码反编译-DLL反编译

路径：/bin/xx.dll

工具：ILSpy

分析流程：

aspx文件内容很少，但会调用bin/目录下的dll文件。

在这里插入图片描述

4、NAT常见安全问题-未授权访问

  • 前台：非法登录会员账号
  • 后台：非法登录管理账号

判断用户身份的方法：

  1. 每个页面（文件）都有判断代码
  2. 一个文件专门用于判断，其他文件包含（调用）它

找未授权漏洞思路：

  • 找哪些文件未包含判断代码文件
  • 判断代码文件是否可以绕过

.NAT比较常见，找源码翻翻。

相关文章：

2、ASPX、.NAT（环境/框架）安全

ASPX、.NAT&#xff08;环境/框架&#xff09;安全 源自小迪安全b站公开课 1、搭建组合&#xff1a; WindowsIISaspxsqlserver .NAT基于windows C开发的框架/环境 对抗Java xx.dll <> xx.jar 关键源码封装在dll文件内。 2、.NAT配置调试-信息泄露 功能点&#xf…...

编程日记 2024/7/14 6:19:35

在家上网IP地址是固定的吗？

在数字化时代&#xff0c;互联网已成为我们日常生活中不可或缺的一部分。无论是工作、学习还是娱乐&#xff0c;我们都离不开网络的支持。然而&#xff0c;当我们在家中接入互联网时&#xff0c;可能会产生这样一个疑问&#xff1a;在家上网IP地址是固定的吗&#xff1f;下面一…...

编程日记 2024/7/14 6:18:33

交换机和路由器的工作流程

1、交换机工作流程&#xff1a; 将接口中的电流识别为二进制&#xff0c;并转换成数据帧&#xff0c;交换机会记录学习该数据帧的源MAC地址&#xff0c;并将其端口关联起来记录在MAC地址表中。然后查看MAC地址表来查找目标MAC地址&#xff0c;会有一下一些情况&#xff1a; MA…...

编程日记 2024/7/14 6:13:29

算法笔记——LCR

一.LCR 152. 验证二叉搜索树的后序遍历序列 题目描述&#xff1a; 给你一个二叉搜索树的后续遍历序列&#xff0c;让你判断该序列是否合法。 解题思路&#xff1a; 根据二叉搜索树的特性&#xff0c;二叉树搜索的每一个结点&#xff0c;大于左子树&#xff0c;小于右子树。…...

编程日记 2024/7/14 6:12:28

ChatGPT对话：如何制作静态网页？

【编者按】编者在很早以前制作过静态网页&#xff0c;之后长期没有使用&#xff0c;已完全不知道最新现状了。所以&#xff0c;从制作工具开始询问ChatGPT&#xff0c;回答非常全面&#xff0c;完全可以解决初学者的问题。 编者虽然长期不制作网页&#xff0c;但一直在编程&…...

编程日记 2024/7/14 6:10:24

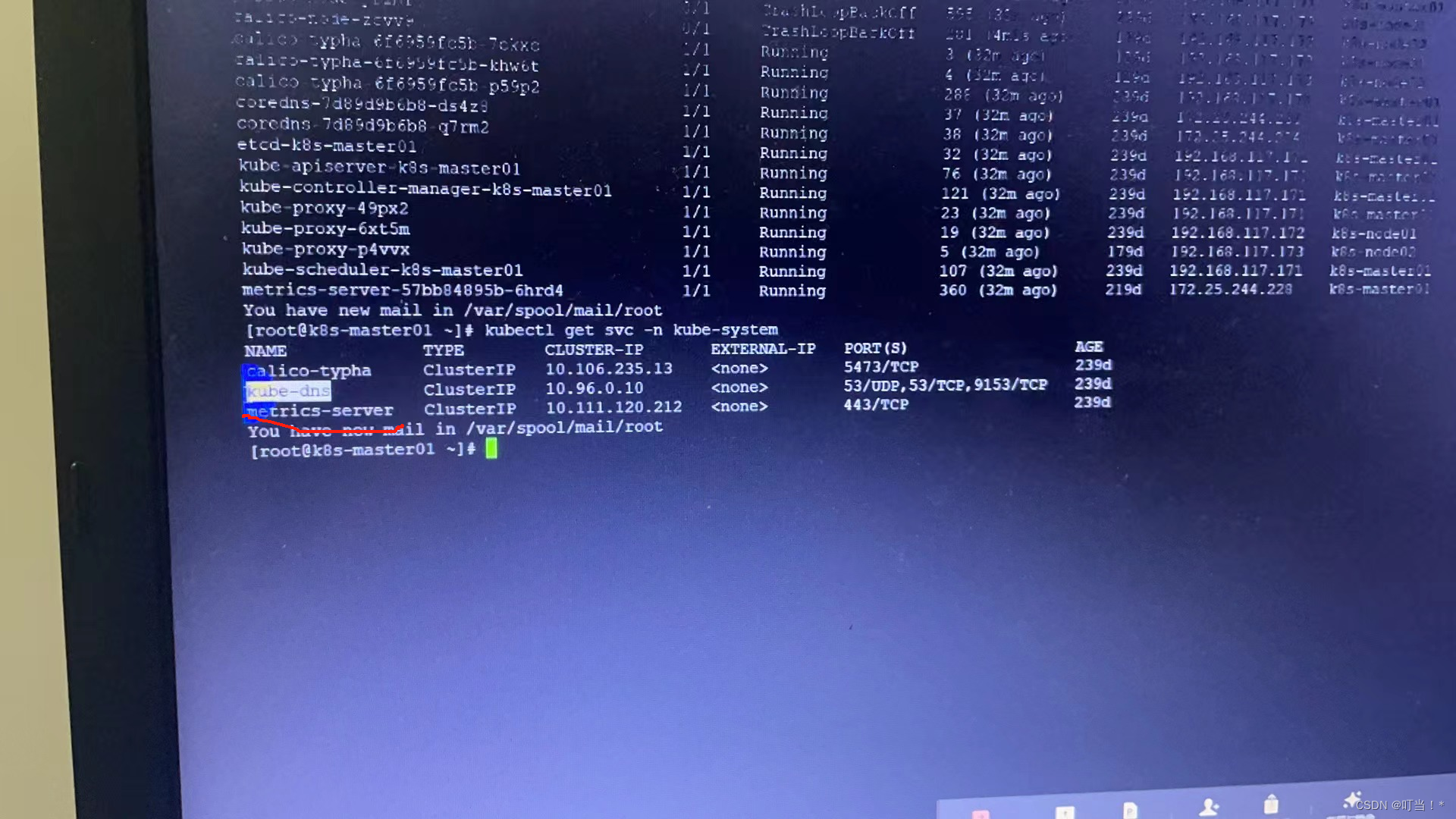
k8s(二）

五、kubernetes架构(K8S的架构也是master和node模式&#xff09; 集群里至少需要有一个master节点&#xff0c;即就是主节点。node节点可以多个。 若是多个master节点&#xff0c;worker节点和master的apiserverr进行交互时&#xff0c;就需要通过LB(load banlance&#xff09;…...

编程日记 2024/7/14 6:09:23

ClickHouse表引擎概述

ClickHouse表引擎概述 表引擎的功能&#xff1a; 数据的存储方式 数据的存储位置 是否可以使用索引 是否可以使用分区 是否支持数据副本 并发数据访问 ClickHouse在建表时必须指定表引擎。 表引擎主要分为四大类&#xff1a;MergeTree系列、Log系列、与其他存储/处理系…...

编程日记 2024/7/14 6:08:22

jenkins系列-04-jenkins参数化构建

使用maven build之前&#xff0c;先checkout 指定分支或标签&#xff1a; 拖拽调整顺序&#xff1a;shell执行在前&#xff0c;构建在后&#xff1a; gitee新建标签tag:...

编程日记 2024/7/14 6:07:21

Flutter框架时间线梳理

Flutter是一个开源的UI工具包&#xff0c;它用于构建高质量的原生移动应用。Flutter的版本历史如下&#xff1a; Flutter 0.1.2&#xff1a; 2018年发布&#xff0c;这是第一个正式发布的版本&#xff0c;包含了基本的框架和工具。 Flutter 1.0.0&#xff1a; 2019年发布&…...

编程日记 2024/7/14 6:06:20

RAG 效果提升的最后一步—— 微调LLM

如果说&#xff0c;rerank能够让RAG的效果实现百尺竿头更进一步&#xff0c;那么LLM微调应该是RAG效果提升的最后一步。 把召回的数据&#xff0c;经过粗排&#xff0c;重排序后&#xff0c;送给模型&#xff0c;由模型最后总结答案。LLM的确已经是RAG的最后一步了。 这里还是会…...

编程日记 2024/7/14 6:05:19

C语言 | Leetcode C语言题解之第230题二叉搜索树中第K小的元素

题目&#xff1a; 题解&#xff1a; /*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/int search_num(struct TreeNode* root, int k, int *result, int num) {if(num k 1){retu…...

编程日记 2024/7/14 6:04:18

YOWOv2(yowov2)动作识别+Fastreid身份识别 详细安装与实现

首先yowov2是一款简单且实时的时空动作检测方案&#xff0c;fastreid是行人重识别&#xff08;身份识别&#xff09; yowov2介绍链接直达fastreid链接直达为时空动作检测任务设计实时框架仍然是一个挑战。YOWOv2 提出了一种新颖的实时动作检测框架&#xff0c;利用三维骨干和二…...

编程日记 2024/7/14 6:02:17

【微服务】Spring Cloud中如何使用Eureka

摘要 Eureka作为Netflix开源的服务发现框架&#xff0c;在Spring Cloud体系中扮演着至关重要的角色。本文详细介绍了Eureka的基本概念、工作原理以及如何在Spring Cloud中集成和使用Eureka进行服务发现和管理。通过深入分析Eureka的注册与发现机制、区域感知和自我保护等高级特…...

编程日记 2024/7/14 6:00:15

【Neo4j】实战 (数据库技术丛书)学习笔记

Neo4j实战 (数据库技术丛书) 第1章演示了应用Neo4j作为图形数据库对改进性能和扩展性的可能性， 也讨论了对图形建模的数据如何正好适应于Neo4j数据模型，现在到了该动 手实践的时间了。第一章 概述 Neo4j将数据作为顶点和边存储（或者用Neo4j术语，节点和关系存 储）。用户被定…...

编程日记 2024/7/14 5:59:14

【Perl】Perl 语言入门

1. Perl语言介绍 Perl 是一种高级、解释型、动态编程语言&#xff0c;由Larry Wall在1987年发布。Perl 以其强大的文本处理能力而闻名&#xff0c;特别是在处理报告生成、文件转换、系统管理任务等方面。它吸收了C、Shell脚本语言、AWK、sed等语言的特性&#xff0c;并加入了大…...

编程日记 2024/7/14 5:58:14

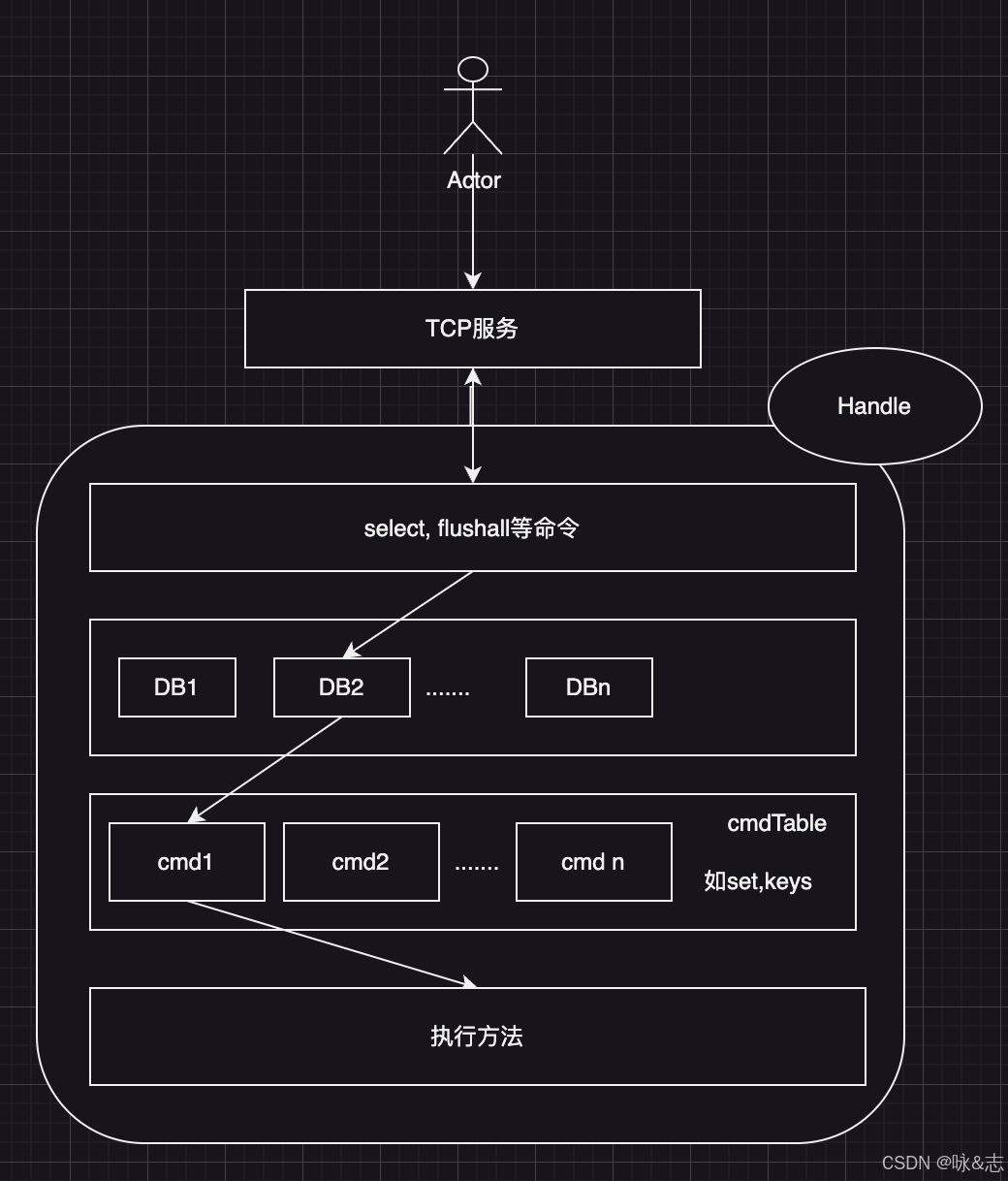
godis源码分析——database存储核心1

前言 redis的核心是数据的快速存储&#xff0c;下面就来分析一下godis的底层存储是如何实现&#xff0c;先分析单机服务。 此文采用抓大放小原则&#xff0c;先大的流程方向&#xff0c;再抓细节。 流程图 源码分析 现在以客户端连接&#xff0c;并发起set key val命令为例…...

编程日记 2024/7/14 5:57:12

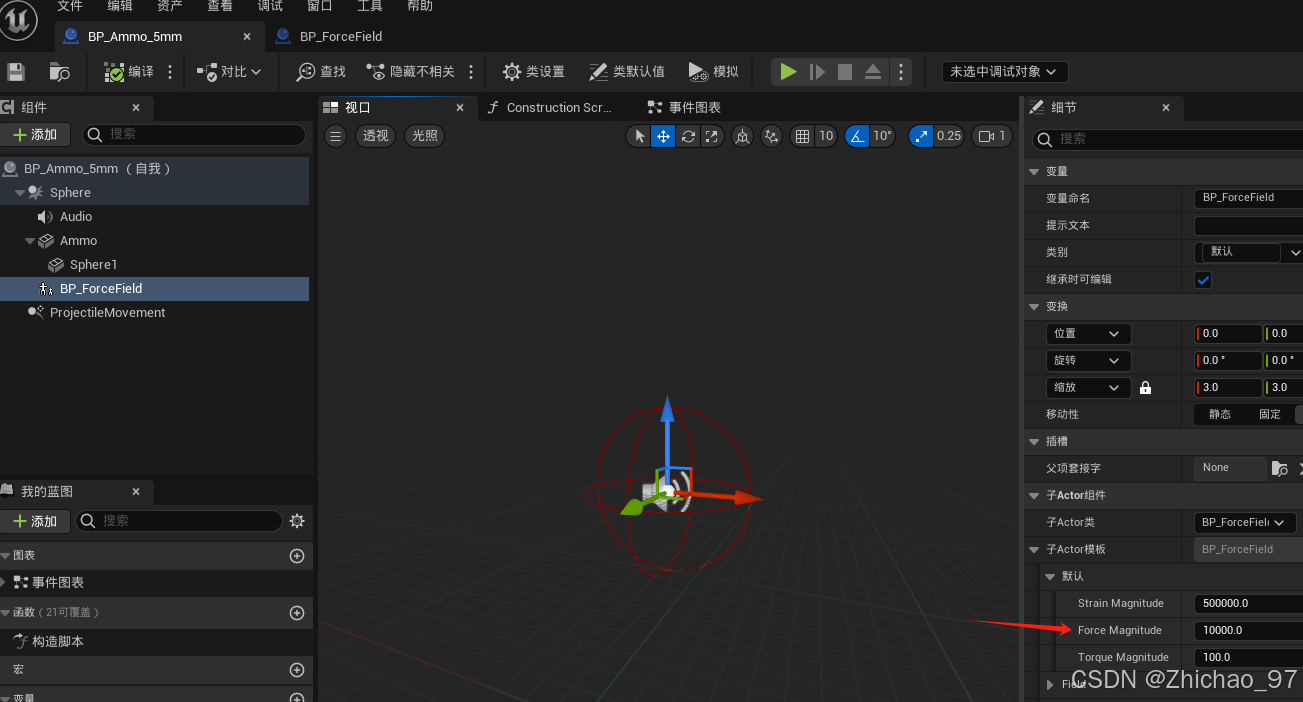
【UE5.1】Chaos物理系统基础——06 子弹破坏石块

前言 在前面我们已经完成了场系统的制作&#xff08;【UE5.1】Chaos物理系统基础——02 场系统的应用_ue5&#xff09;以及子弹的制作&#xff08;【UE5.1 角色练习】16-枪械射击——瞄准&#xff09;&#xff0c;现在我们准备实现的效果是&#xff0c;角色发射子弹来破坏石柱。…...

编程日记 2024/7/14 5:55:10

Django是干什么的？好用么？

Django是一个开源的Python Web框架&#xff0c;用于快速开发高质量的Web应用程序。它提供了许多功能和工具&#xff0c;以简化常见的Web开发任务&#xff0c;如路由、请求处理、数据库管理等。 Django的优点包括&#xff1a; 简单易用&#xff1a;Django提供了清晰的文档和丰…...

编程日记 2024/7/14 5:54:09

C语言实现数据结构B树

B树&#xff08;B-Tree&#xff09;是一种自平衡的树数据结构&#xff0c;它维护着数据的有序性&#xff0c;并允许搜索、顺序访问、插入、删除等操作都在对数时间内完成。B树广泛用于数据库和操作系统的文件系统中。 B树的基本特性 根节点&#xff1a;根节点至少有两个子节点…...

编程日记 2024/7/14 5:52:07

[论文阅读]MaIL: Improving Imitation Learning with Mamba

Abstract 这项工作介绍了mamba模仿学习&#xff08;mail&#xff09;&#xff0c;这是一种新颖的模仿学习&#xff08;il&#xff09;架构&#xff0c;为最先进的&#xff08;sota&#xff09;变换器策略提供了一种计算高效的替代方案。基于变压器的策略由于能够处理具有固有非…...

编程日记 2024/7/14 5:51:07

调用支付宝接口响应40004 SYSTEM_ERROR问题排查

在对接支付宝API的时候&#xff0c;遇到了一些问题&#xff0c;记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

编程新知 2025/10/17 20:43:55

【Go】3、Go语言进阶与依赖管理

前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课&#xff0c;做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程&#xff0c;它的核心机制是 Goroutine 协程、Channel 通道&#xff0c;并基于CSP&#xff08;Communicating Sequential Processes&#xff0…...

编程新知 2025/10/7 0:32:40

高防服务器能够抵御哪些网络攻击呢？

高防服务器作为一种有着高度防御能力的服务器&#xff0c;可以帮助网站应对分布式拒绝服务攻击&#xff0c;有效识别和清理一些恶意的网络流量&#xff0c;为用户提供安全且稳定的网络环境&#xff0c;那么&#xff0c;高防服务器一般都可以抵御哪些网络攻击呢&#xff1f;下面…...

编程新知 2025/9/3 19:14:38

C++八股 —— 单例模式

文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全&#xff08;Thread Safety&#xff09; 线程安全是指在多线程环境下&#xff0c;某个函数、类或代码片段能够被多个线程同时调用时&#xff0c;仍能保证数据的一致性和逻辑的正确性&#xf…...

编程新知 2025/10/13 7:34:19

Element Plus 表单(el-form)中关于正整数输入的校验规则

目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入&#xff08;联动&#xff09;2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

编程新知 2025/10/29 9:58:23

3-11单元格区域边界定位(End属性)学习笔记

返回一个Range 对象&#xff0c;只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意&#xff1a;它移动的位置必须是相连的有内容的单元格…...

编程新知 2025/10/30 4:32:03

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案

这个问题我看其他博主也写了&#xff0c;要么要会员、要么写的乱七八糟。这里我整理一下&#xff0c;把问题说清楚并且给出代码&#xff0c;拿去用就行&#xff0c;照着葫芦画瓢。 问题 在继承QWebEngineView后&#xff0c;重写mousePressEvent或event函数无法捕获鼠标按下事…...

编程新知 2025/6/11 3:07:32

嵌入式常见 CPU 架构

架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集&#xff0c;单周期执行&#xff1b;低功耗、CIP 独立外设&#xff1b;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel&#xff08;原始…...

编程新知 2025/6/10 21:24:01

c# 局部函数 定义、功能与示例

C# 局部函数&#xff1a;定义、功能与示例 1. 定义与功能 局部函数&#xff08;Local Function&#xff09;是嵌套在另一个方法内部的私有方法&#xff0c;仅在包含它的方法内可见。 • 作用&#xff1a;封装仅用于当前方法的逻辑&#xff0c;避免污染类作用域&#xff0c;提升…...

编程新知 2025/9/18 4:17:51

第八部分：阶段项目 6：构建 React 前端应用

现在&#xff0c;是时候将你学到的 React 基础知识付诸实践&#xff0c;构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段&#xff0c;你可以先使用模拟数据&#xff0c;或者如果你的后端 API&#xff08;阶段项目 5&#xff09;已经搭建好&#xff0c;可以直接连…...

编程新知 2025/9/21 1:58:01