C语言实现数据结构B树
B树(B-Tree)是一种自平衡的树数据结构,它维护着数据的有序性,并允许搜索、顺序访问、插入、删除等操作都在对数时间内完成。B树广泛用于数据库和操作系统的文件系统中。
B树的基本特性
- 根节点:根节点至少有两个子节点(除非它是叶子节点)。
- 内部节点:每个内部节点包含的关键字(或称“键”)数量m满足⌈m/2⌉ - 1 ≤ n ≤ m - 1,其中n是节点中关键字的数量,m是节点的最大容量(对于所有节点相同)。
- 叶子节点:所有叶子节点都在同一层上,并且不带信息(或带有指向数据记录的指针),也可以包含关键字信息。
- 分裂与合并:当节点中的关键字数量超过m-1时,该节点分裂成两个节点;当节点中的关键字数量少于⌈m/2⌉-1时,可能通过与其兄弟节点合并来避免这种情况。
- 关键字排序:节点内的关键字按升序排列,使得每个关键字都是其左子树所有值的最大值,也是其右子树所有值的最小值(对于非叶子节点)。
B树的C语言实现概述
这里我们不会完整地实现一个B树,但会展示一些关键部分,如节点结构定义、插入和分裂的简化逻辑。
节点结构定义
#include <stdio.h>
#include <stdlib.h> #define MAX_KEYS 4 // 假设每个节点的最大关键字数量为4 typedef struct BTreeNode { int keys[MAX_KEYS]; // 存储关键字 int numKeys; // 当前节点中关键字的数量 struct BTreeNode *children[MAX_KEYS + 1]; // 子节点指针数组,比关键字数多一个 struct BTreeNode *parent; // 父节点指针 int isLeaf; // 标记是否为叶子节点
} BTreeNode; // 初始化节点
BTreeNode* createNode(int isLeaf) { BTreeNode* node = (BTreeNode*)malloc(sizeof(BTreeNode)); node->numKeys = 0; node->parent = NULL; node->isLeaf = isLeaf; for (int i = 0; i <= MAX_KEYS; i++) { node->children[i] = NULL; } return node;
}
插入操作(简化版)
插入操作涉及在树中找到合适的位置插入新关键字,并在必要时分裂节点。这里只提供一个概念性的伪代码:
// 假设已有函数insertNonFull,用于向非满节点中插入关键字
void insert(BTreeNode* root, int key) { if (root == NULL) { // 创建新的根节点 root = createNode(1); // 假设根节点总是叶子 root->keys[0] = key; root->numKeys = 1; } else { // 找到插入的位置 BTreeNode* node = findLeaf(root, key); // 假设有findLeaf函数 // 插入到叶子节点 if (node->numKeys < MAX_KEYS) { insertNonFull(node, key); } else { // 节点已满,需要分裂 splitChild(node, findInsertPos(node->keys, node->numKeys, key)); // 递归向上调整父节点 // 可能需要再次分裂父节点 } }
}
注意:上述代码是高度简化的,并未实现findLeaf、insertNonFull、findInsertPos、splitChild等函数,这些函数是实现B树的关键。
结论
B树的实现涉及复杂的逻辑和多种情况的处理,特别是节点的分裂和合并。在实际应用中,你可能需要查阅更多的资料或使用现成的库来处理这些复杂的数据结构。上述代码和解释旨在提供一个关于B树基本概念和实现的起点。
相关文章:

C语言实现数据结构B树
B树(B-Tree)是一种自平衡的树数据结构,它维护着数据的有序性,并允许搜索、顺序访问、插入、删除等操作都在对数时间内完成。B树广泛用于数据库和操作系统的文件系统中。 B树的基本特性 根节点:根节点至少有两个子节点…...

[论文阅读]MaIL: Improving Imitation Learning with Mamba
Abstract 这项工作介绍了mamba模仿学习(mail),这是一种新颖的模仿学习(il)架构,为最先进的(sota)变换器策略提供了一种计算高效的替代方案。基于变压器的策略由于能够处理具有固有非…...

在HTML中使用JavaScript
在 HTML 中使用 JavaScript 有以下几种常见的方式: 一、内联脚本 (一)基本语法 内联脚本是将 JavaScript 代码直接嵌入到 HTML 文件的 <script> 标签内部。 <!DOCTYPE html> <html lang"en"> <head> <…...
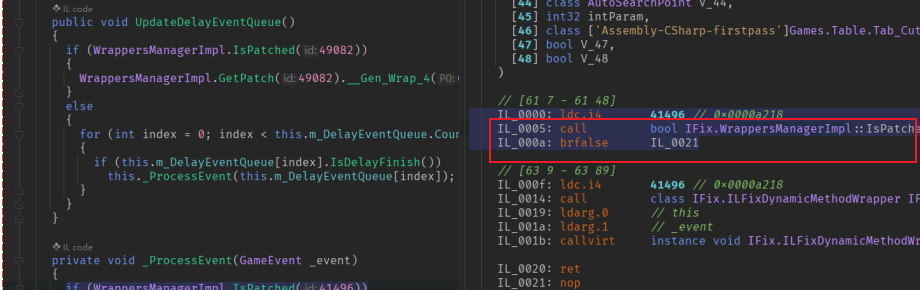
InjectFix 热更新解决方案
简介 今天来谈一谈,项目种的客户端热更新解决方案。InjectFix是腾讯xlua团队出品的一种用于Unity中C#代码热更新热修复的解决方案。支持Unity全系列,全平台。与xlua的思路类似,InjectFix解决的痛点主要在于Unity中C#代码写的逻辑在发包之后无…...
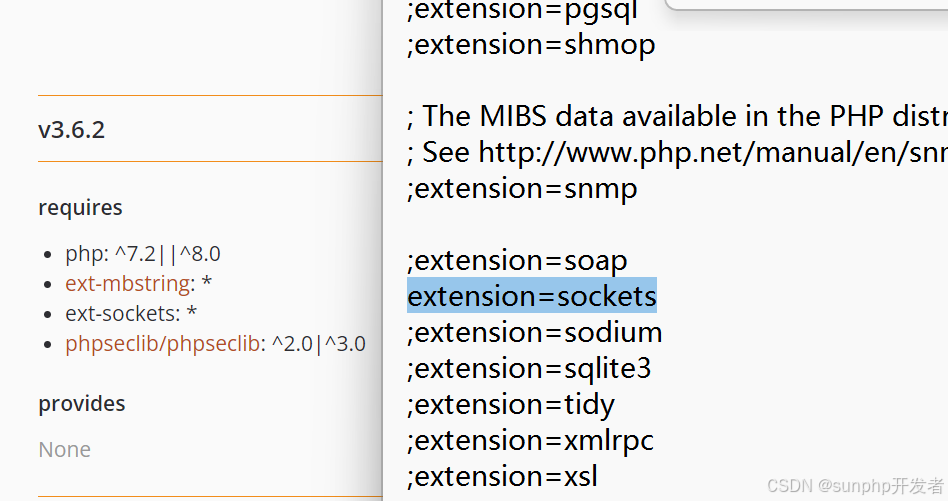
PHP7.4安装使用rabbitMQ教程(windows)
(1),安装rabbitMQ客户端erlang语言 一,erlang语言安装 下载地址1—— 下载地址2——https://www.erlang.org/patches/otp-27.0 二,rabbitMQ客户端安装 https://www.rabbitmq.com/docs/install-windows (…...
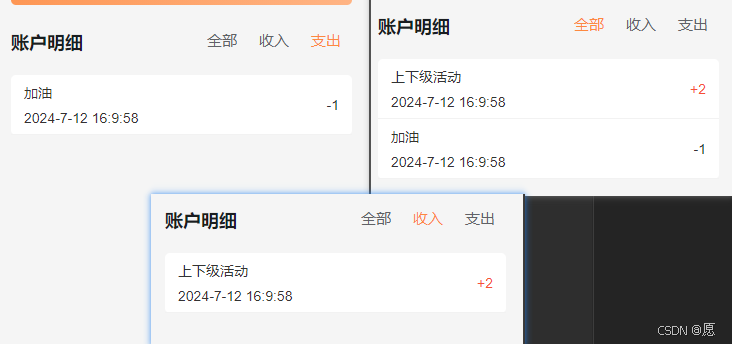
分页以及tab栏切换,动态传类型
<view class"disTitle"><view class"disName">账户明细</view><view class"nav"><u-tabs lineWidth"0" :activeStyle"{color: #FD893F }" :list"navList" change"tabsChange&quo…...

【算法】平衡二叉树
难度:简单 题目 给定一个二叉树,判断它是否是 平衡二叉树 示例: 示例1: 输入:root [3,9,20,null,null,15,7] 输出:true 示例2: 输入:root [1,2,2,3,3,null,null,4,4] 输出&…...

五、 计算机网络(考点篇)
1 网络概述和模型 计算机网络是计算机技术与通信技术相结合的产物,它实现了远程通信、远程信息处理和资源共享。计算机网络的功能:数据通信、资源共享、管理集中化、实现分布式处理、负载均衡。 网络性能指标:速率、带宽(频带宽度或传送线路…...

如何解决数据分析问题:IPython与Pandas结合
如何解决数据分析问题:IPython与Pandas结合 数据分析是现代科学研究、商业决策和技术开发中的一个重要环节。IPython和Pandas是两个强大的工具,它们可以大大简化和加速数据分析的过程。本文将为初学者详细介绍如何结合使用IPython和Pandas来解决数据分析…...

如何在 Microsoft Edge 上使用开发人员工具
Microsoft Edge 提供了一套强大的开发人员工具,可帮助 Web 开发人员检查、调试和优化他们的网站或 Web 应用程序。 无论您是经验丰富的 Web 开发人员还是刚刚起步,了解如何有效地使用这些工具都可以对开发过程产生重大影响。 在本文中,我们…...

《Linux系统编程篇》认识在linux上的文件 ——基础篇
前言 Linux系统编程的文件操作如同掌握了一把魔法钥匙,打开了无尽可能性的大门。在这个世界中,你需要了解文件描述符、文件权限、文件路径等基础知识,就像探险家需要了解地图和指南针一样。而了解这些基础知识,就像学会了魔法咒语…...

Qt:22.鼠标相关事件(实例演示——鼠标进入/离开某控件的事件、鼠标按下事件、鼠标释放事件、鼠标双击事件)
目录 1.实例演示——鼠标进入/离开某控件的事件: 2.鼠标按下事件: 3.鼠标释放事件: 4.鼠标双击事件: 1.实例演示——鼠标进入/离开某控件的事件: 首先创建一个C类文件 Label,填写好要继承的父类 QLabe…...

笔记 4 :linux 0.11 中继续分析 0 号进程创建一号进程的 fork () 函数
(27)本条目开始, 开始分析 copy_process () 函数,其又会调用别的函数,故先分析别的函数。 get_free_page () ; 先 介绍汇编指令 scasb : 以及 指令 sstosd :…...

Vue3 引入Vanta.js使用
能搜到这篇文章 想必一定看过demo效果图了吧 示例 Vanta.js - Animated 3D Backgrounds For Your Website (vantajs.com) 1. 引入 在根目录 index.html中引入依赖 <script src"https://cdnjs.cloudflare.com/ajax/libs/three.js/r134/three.min.js"></sc…...

LeetCode --- 134双周赛
题目 3206. 交替组 I 3207. 与敌人战斗后的最大分数 3208. 交替组 II 3209. 子数组按位与值为 K 的数目 一、交替组 I & II 题目中问环形数组中交替组的长度为3的子数组个数,主要的问题在于它是环形的,我们要考虑首尾相接的情况,如何…...

快速读出linux 内核中全局变量
查问题时发现全局变量能读出来会提高效率,于是考虑从怎么读出内核态的全局变量,脚本如下 f open("/proc/kcore", rb) f.seek(4) # skip magic assert f.read(1) b\x02 # 64 位def read_number(bytes):return int.from_bytes(bytes, little,…...

postman录制设置
一、前言: postman是一个很好接口调试或是测试工具,简单方便,不需要很复杂的流程与技术,并且也具备录制条件。对于接口不了解,没有明确对应的说明,但又想通过接口进行一些测试使用其录制是一个不错的办…...

redis消息队列
redis 的list类型实现消息队列: list结构实现的优缺点: 2、pubsub模式(消息发布订阅)实现消息队列 pubsub的优缺点: 命令行实现: pub:第一次发送有两个接收,第二个只有一个接收 sub接收&#x…...

Linux vim的使用(一键安装则好用的插件_forcpp),gcc的常见编译链接操作
vim 在Linux系统上vim是个功能还比较完善的软件。但是没装插件的vim用着还是挺难受的,所以我们直接上一款插件。 我们只需要在Linux上执行这个命令就能安装(bite提供的) curl -sLf https://gitee.com/HGtz2222/VimForCpp/raw/master/install.sh -o ./install.sh …...

css基础(1)
CSS CCS Syntax CSS 规则由选择器和声明块组成。 CSS选择器 CSS选择器用于查找想要设置样式的HTML元素 一般选择器分为五类 Simple selectors (select elements based on name, id, class) 简单选择器(根据名称、id、类选择元素) //页面上的所有 …...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...
