泰勒级数 (Taylor Series) 动画展示 包括源码
泰勒级数 (Taylor Series) 动画展示 包括源码
flyfish
泰勒级数(英语:Taylor series)用无限项连加式 - 级数来表示一个函数,这些相加的项由函数在某一点的导数求得。
定义了一个函数f(x)表示要近似的函数 sin ( x ) \sin(x) sin(x),以及一个函数taylor_series(x, n)来计算泰勒级数的前n项。动画展示了泰勒级数如何逐步逼近 sin ( x ) \sin(x) sin(x)函数。这个例子展示了泰勒级数的逼近效果,以及随着项数的增加,近似效果变得更好。

)
级数 (Series)
定义
级数是数列求和的过程。具体来说,给定一个数列 a 1 , a 2 , a 3 , … a_1, a_2, a_3, \ldots a1,a2,a3,…,它的级数是所有项相加得到的总和: S = a 1 + a 2 + a 3 + ⋯ S = a_1 + a_2 + a_3 + \cdots S=a1+a2+a3+⋯
通常我们会使用符号表示:
S = ∑ n = 1 ∞ a n S = \sum_{n=1}^{\infty} a_n S=n=1∑∞an
收敛与发散
一个级数可以是收敛的,也可以是发散的。如果级数的部分和 S n = ∑ n = 1 N a n S_n = \sum_{n=1}^{N} a_n Sn=∑n=1Nan 在 N N N 趋向于无穷大时趋向于某个有限的值 L L L,则称该级数是收敛的,记作: ∑ n = 1 ∞ a n = L \sum_{n=1}^{\infty} a_n = L n=1∑∞an=L
否则称该级数是发散的。
泰勒级数 (Taylor Series)
定义
泰勒级数是一种特殊的级数,用于表示一个函数在某点附近的近似。对于一个在 x = a x = a x=a 点具有 n n n 阶可导数的函数 f ( x ) f(x) f(x),它的泰勒级数可以表示为: f ( x ) = f ( a ) + f ′ ( a ) ( x − a ) + f ′ ′ ( a ) 2 ! ( x − a ) 2 + f ′ ′ ′ ( a ) 3 ! ( x − a ) 3 + ⋯ f(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \frac{f'''(a)}{3!}(x-a)^3 + \cdots f(x)=f(a)+f′(a)(x−a)+2!f′′(a)(x−a)2+3!f′′′(a)(x−a)3+⋯
一般地,泰勒级数的形式为:
f ( x ) = ∑ n = 0 ∞ f ( n ) ( a ) n ! ( x − a ) n f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!} (x - a)^n f(x)=n=0∑∞n!f(n)(a)(x−a)n其中, f ( n ) ( a ) f^{(n)}(a) f(n)(a) 表示函数 f ( x ) f(x) f(x) 在 x = a x = a x=a 处的第 n n n 阶导数, n ! n! n! 表示 n n n 的阶乘。
麦克劳林级数
泰勒级数在 a = 0 a = 0 a=0 时的特殊形式称为麦克劳林级数(Maclaurin Series): f ( x ) = f ( 0 ) + f ′ ( 0 ) x + f ′ ′ ( 0 ) 2 ! x 2 + f ′ ′ ′ ( 0 ) 3 ! x 3 + ⋯ f(x) = f(0) + f'(0)x + \frac{f''(0)}{2!}x^2 + \frac{f'''(0)}{3!}x^3 + \cdots f(x)=f(0)+f′(0)x+2!f′′(0)x2+3!f′′′(0)x3+⋯
即:
f ( x ) = ∑ n = 0 ∞ f ( n ) ( 0 ) n ! x n f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(0)}{n!} x^n f(x)=n=0∑∞n!f(n)(0)xn
例子
用无限项连加式——级数来表示一个函数,这些相加的项由函数在某一点的导数求得。
1. 指数函数的泰勒级数
对于函数 e x e^x ex,它在 x = 0 x = 0 x=0 处的泰勒级数(也是麦克劳林级数)为: e x = 1 + x + x 2 2 ! + x 3 3 ! + ⋯ = ∑ n = 0 ∞ x n n ! e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots = \sum_{n=0}^{\infty} \frac{x^n}{n!} ex=1+x+2!x2+3!x3+⋯=n=0∑∞n!xn
2. 正弦函数的泰勒级数
对于函数 sin ( x ) \sin(x) sin(x),它在 x = 0 x = 0 x=0 处的泰勒级数(麦克劳林级数)为: sin ( x ) = x − x 3 3 ! + x 5 5 ! − ⋯ = ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 ( 2 n + 1 ) ! \sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots = \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n+1}}{(2n+1)!} sin(x)=x−3!x3+5!x5−⋯=n=0∑∞(2n+1)!(−1)nx2n+1
前几项展开式为:
sin ( x ) ≈ x − x 3 3 ! + x 5 5 ! − x 7 7 ! + ⋯ \sin(x) \approx x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots sin(x)≈x−3!x3+5!x5−7!x7+⋯
通过增加项数,可以使泰勒多项式对原函数的近似更加精确。
动画源码
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation# 定义泰勒级数逼近的项数
N = 10# 定义函数和泰勒级数的函数
def f(x):return np.sin(x)def taylor_series(x, n):result = 0for i in range(n + 1):result += ((-1)**i * x**(2 * i + 1)) / np.math.factorial(2 * i + 1)return result# 创建图形和轴
fig, ax = plt.subplots()
x = np.linspace(-2 * np.pi, 2 * np.pi, 1000)
y = f(x)
line, = ax.plot(x, y, label='sin(x)')
line_taylor, = ax.plot([], [], label='Taylor Series')
ax.set_ylim(-2, 2)
ax.legend()# 初始化函数
def init():line_taylor.set_data([], [])return line_taylor,# 更新函数
def update(n):y_taylor = taylor_series(x, n)line_taylor.set_data(x, y_taylor)ax.set_title(f'Taylor Series Approximation with {n} terms')return line_taylor,# 创建动画
ani = animation.FuncAnimation(fig, update, frames=N, init_func=init, blit=True)# 保存动画为GIF
ani.save('taylor_series_approximation.gif', writer='imagemagick')plt.show()
应用
用泰勒级数在某一点上近似计算一个函数的值。
使用泰勒级数近似计算 e x e^x ex 在 x = 0.1 x = 0.1 x=0.1 处的值, e x e^x ex 的泰勒级数(在 x = 0 x = 0 x=0 处展开)是: e x = 1 + x + x 2 2 ! + x 3 3 ! + x 4 4 ! + ⋯ e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \cdots ex=1+x+2!x2+3!x3+4!x4+⋯为了近似计算 e 0.1 e^{0.1} e0.1,我们可以只取前几项进行计算。
第一步:计算各项的值
-
x = 0.1 x = 0.1 x=0.1
-
e x ≈ 1 + x + x 2 2 ! + x 3 3 ! + x 4 4 ! e^x \approx 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} ex≈1+x+2!x2+3!x3+4!x4
第二步:逐项计算
-
第一项: 1 1 1
-
第二项: 0.1 0.1 0.1
-
第三项: ( 0.1 ) 2 2 ! = 0.01 2 = 0.005 \frac{(0.1)^2}{2!} = \frac{0.01}{2} = 0.005 2!(0.1)2=20.01=0.005
-
第四项: ( 0.1 ) 3 3 ! = 0.001 6 ≈ 0.000167 \frac{(0.1)^3}{3!} = \frac{0.001}{6} \approx 0.000167 3!(0.1)3=60.001≈0.000167
-
第五项: ( 0.1 ) 4 4 ! = 0.0001 24 ≈ 0.00000417 \frac{(0.1)^4}{4!} = \frac{0.0001}{24} \approx 0.00000417 4!(0.1)4=240.0001≈0.00000417
第三步:求和
将这些项相加:
e 0.1 ≈ 1 + 0.1 + 0.005 + 0.000167 + 0.00000417 ≈ 1.10517117 e^{0.1} \approx 1 + 0.1 + 0.005 + 0.000167 + 0.00000417 \approx 1.10517117 e0.1≈1+0.1+0.005+0.000167+0.00000417≈1.10517117
第四步:与实际值比较
用计算器计算 e 0.1 e^{0.1} e0.1 的实际值: e 0.1 ≈ 1.105170918 e^{0.1} \approx 1.105170918 e0.1≈1.105170918我们看到,使用泰勒级数前几项的近似值 1.10517117 1.10517117 1.10517117 与实际值 1.105170918 1.105170918 1.105170918 非常接近,误差在 1 0 − 6 10^{-6} 10−6 量级上。
这个例子展示了如何使用泰勒级数在某一点上近似计算一个函数的值。通过逐项计算并求和,我们可以得到一个非常接近实际值的近似结果。
绘制不同项数的泰勒级数曲线,比较近似值和实际值

import numpy as np
import matplotlib.pyplot as plt# 定义 e^x 的泰勒级数近似函数
def taylor_series_exp(x, n_terms):taylor_sum = 0for n in range(n_terms):taylor_sum += (x**n) / np.math.factorial(n)return taylor_sum# 定义实际的 e^x 函数
def actual_exp(x):return np.exp(x)# x 的范围
x_values = np.linspace(-1, 1, 400)# 不同项数的泰勒级数近似
terms_list = [1, 2, 3, 5, 10] # 泰勒级数的项数列表# 创建图形
plt.figure(figsize=(10, 6))# 绘制实际的 e^x 曲线
plt.plot(x_values, actual_exp(x_values), label='Actual $e^x$', color='blue')# 绘制不同项数的泰勒级数近似曲线
colors = ['red', 'orange', 'green', 'purple', 'brown']
for i, n_terms in enumerate(terms_list):taylor_values = [taylor_series_exp(x, n_terms) for x in x_values]plt.plot(x_values, taylor_values, label=f'Taylor Series (n={n_terms})', color=colors[i], linestyle='--')# 标注在 x=0.1 处的点
plt.scatter(0.1, taylor_series_exp(0.1, 5), color='green', zorder=5, label='Approximation at x=0.1')
plt.scatter(0.1, actual_exp(0.1), color='purple', zorder=5, label='Actual at x=0.1')# 标注和标签
plt.xlabel('x')
plt.ylabel('y')
plt.title('Taylor Series Approximation of $e^x$')
plt.legend()
plt.grid(True)
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.show()# 打印在 x=0.1 处的近似值和实际值
approx_value = taylor_series_exp(0.1, 5)
actual_value = actual_exp(0.1)
print(f'Taylor Series Approximation at x=0.1 with n=5: {approx_value}')
print(f'Actual value at x=0.1: {actual_value}')
数学思想的演变
古希腊时期
芝诺悖论:古希腊哲学家芝诺提出了著名的芝诺悖论,探讨了如何利用无穷级数求和来得到有限结果的问题。芝诺的结论是无法完成的,这在当时引发了广泛的讨论和争论。
亚里士多德:亚里士多德对芝诺悖论进行了哲学上的反驳,但并没有解决数学上的问题。
德谟克利特和阿基米德:德谟克利特和后来著名的数学家阿基米德进一步研究了无穷级数问题。阿基米德利用穷竭法,逐步细分无穷级数,从而得到了有限的结果。这种方法为后来的数学发展奠定了基础。
中国古代
刘徽:几个世纪之后,中国数学家刘徽也独立提出了类似于穷竭法的方法,用于解决类似的问题。他的工作与阿基米德的穷竭法有很多相似之处。
中世纪
马德哈瓦:进入14世纪,印度数学家马德哈瓦是最早使用泰勒级数及相关方法的数学家之一。尽管他的数学著作没有流传下来,但后来印度数学家的著作表明他发现了一些特殊的泰勒级数,这些级数包括正弦、余弦、正切、和反正切三角函数等。喀拉拉学派在他的基础上进行了延伸和合理逼近,这些工作一直持续到16世纪。
17世纪
詹姆斯·格雷果里:在17世纪,詹姆斯·格雷果里继续这方面的研究,并发表了若干麦克劳林级数的相关工作。
18世纪
布鲁克·泰勒:直到1715年,布鲁克·泰勒提出了一个通用的方法来构建适用于所有函数的级数,这就是后来的泰勒级数。泰勒的方法能够用于构建各种函数的无穷级数表示,使得这一概念成为数学分析中的重要工具。
科林·麦克劳林:麦克劳林级数是泰勒级数的特例,是由爱丁堡大学的科林·麦克劳林教授在18世纪发表的,并以其名字命名。
泰勒级数展开
泰勒级数展开与直线方程的关系
泰勒级数是基于函数在某一点 x 0 x_0 x0 处的所有阶导数来展开的。公式为:
f ( x ) ≈ f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) 1 ! + f ′ ′ ( x 0 ) ( x − x 0 ) 2 2 ! + ⋯ + f ( n ) ( x 0 ) ( x − x 0 ) n n ! f(x) \approx f(x_0) + f'(x_0) \frac{(x - x_0)}{1!} + f''(x_0) \frac{(x - x_0)^2}{2!} + \cdots + f^{(n)}(x_0) \frac{(x - x_0)^n}{n!} f(x)≈f(x0)+f′(x0)1!(x−x0)+f′′(x0)2!(x−x0)2+⋯+f(n)(x0)n!(x−x0)n当 n n n 趋于无穷时,该级数可以等于函数本身:
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + ⋯ + f ( n ) ( x 0 ) n ! ( x − x 0 ) n + ⋯ f(x) = f(x_0) + f'(x_0) (x - x_0) + \frac{f''(x_0)}{2!} (x - x_0)^2 + \cdots + \frac{f^{(n)}(x_0)}{n!} (x - x_0)^n + \cdots f(x)=f(x0)+f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+⋯+n!f(n)(x0)(x−x0)n+⋯
一阶展开(线性近似)
如果只考虑泰勒级数的前两项,得到函数在 x 0 x_0 x0 处的线性近似,也叫做一阶泰勒展开:
f ( x ) ≈ f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) f(x) \approx f(x_0) + f'(x_0) (x - x_0) f(x)≈f(x0)+f′(x0)(x−x0)
这是因为所有高于一次项的项都被忽略了。
直线方程的推导
一阶泰勒展开的形式与直线方程形式一致。可以将 f ( x ) ≈ f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) f(x) \approx f(x_0) + f'(x_0) (x - x_0) f(x)≈f(x0)+f′(x0)(x−x0) 写成直线方程:
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) f(x) = f(x_0) + f'(x_0) (x - x_0) f(x)=f(x0)+f′(x0)(x−x0)如果令:
f ( x 0 ) = k 1 f(x_0) = k_1 f(x0)=k1
f ′ ( x 0 ) = k 2 f'(x_0) = k_2 f′(x0)=k2那么上述方程变为:
f ( x ) = k 1 + k 2 ( x − x 0 ) f(x) = k_1 + k_2 (x - x_0) f(x)=k1+k2(x−x0)这就是直线的方程形式,其中 k 1 k_1 k1 是直线在 x = x 0 x = x_0 x=x0 处的函数值(即截距), k 2 k_2 k2 是直线的斜率(即导数)。线性近似的应用: x \sqrt{x} x的例子找到 f ( x ) = x f(x) = \sqrt{x} f(x)=x 在 x = 9 x = 9 x=9 处的线性近似,并估算 9.1 \sqrt{9.1} 9.1:
-
计算 f ( 9 ) f(9) f(9):
f ( 9 ) = 9 = 3 f(9) = \sqrt{9} = 3 f(9)=9=3 -
计算 f ′ ( x ) f'(x) f′(x) 并在 x = 9 x = 9 x=9 处求导:
f ′ ( x ) = 1 2 x f'(x) = \frac{1}{2\sqrt{x}} f′(x)=2x1
f ′ ( 9 ) = 1 2 9 = 1 6 f'(9) = \frac{1}{2\sqrt{9}} = \frac{1}{6} f′(9)=291=61 -
代入线性近似公式:
L ( x ) = f ( 9 ) + f ′ ( 9 ) ( x − 9 ) L(x) = f(9) + f'(9)(x - 9) L(x)=f(9)+f′(9)(x−9)
L ( x ) = 3 + 1 6 ( x − 9 ) L(x) = 3 + \frac{1}{6}(x - 9) L(x)=3+61(x−9) -
估算 9.1 \sqrt{9.1} 9.1:
L ( 9.1 ) = 3 + 1 6 ( 9.1 − 9 ) L(9.1) = 3 + \frac{1}{6}(9.1 - 9) L(9.1)=3+61(9.1−9)
L ( 9.1 ) = 3 + 1 6 ( 0.1 ) L(9.1) = 3 + \frac{1}{6}(0.1) L(9.1)=3+61(0.1)
L ( 9.1 ) = 3 + 0.0167 ≈ 3.0167 L(9.1) = 3 + 0.0167 \approx 3.0167 L(9.1)=3+0.0167≈3.0167
所以, 9.1 ≈ 3.0167 \sqrt{9.1} \approx 3.0167 9.1≈3.0167。
通过泰勒级数的一阶展开,可以得到函数在某一点附近的线性近似。
另一种描述方式
y = m x + b y = mx + b y=mx+b其中 m m m 是斜率, b b b 是截距。对于一阶泰勒展开,可以将其写成类似直线方程的形式:
y = f ( x ) y = f(x) y=f(x)
m = f ′ ( x 0 ) m = f'(x_0) m=f′(x0)
b = f ( x 0 ) − f ′ ( x 0 ) x 0 b = f(x_0) - f'(x_0)x_0 b=f(x0)−f′(x0)x0实际上,一阶泰勒展开的形式 f ( x ) ≈ f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) f(x) \approx f(x_0) + f'(x_0)(x - x_0) f(x)≈f(x0)+f′(x0)(x−x0) 正是线性函数的形式,其中:
f ( x 0 ) f(x_0) f(x0) 表示在 x = x 0 x = x_0 x=x0 处的函数值,是线性函数的截距;
f ′ ( x 0 ) f'(x_0) f′(x0) 表示在 x = x 0 x = x_0 x=x0 处的导数,是线性函数的斜率。
相关文章:

泰勒级数 (Taylor Series) 动画展示 包括源码
泰勒级数 (Taylor Series) 动画展示 包括源码 flyfish 泰勒级数(英语:Taylor series)用无限项连加式 - 级数来表示一个函数,这些相加的项由函数在某一点的导数求得。 定义了一个函数f(x)表示要近似的函数 sin ( x ) \sin(x) …...

蔚来汽车:拥抱TiDB,实现数据库性能与稳定性的飞跃
作者: Billdi表弟 原文来源: https://tidb.net/blog/449c3f5b 演讲嘉宾:吴记 蔚来汽车Tidb爱好者 整理编辑:黄漫绅(表妹)、李仲舒、吴记 本文来自 TiDB 社区合肥站走进蔚来汽车——来自吴记老师的演讲…...

【Django+Vue3 线上教育平台项目实战】构建高效线上教育平台之首页模块
文章目录 前言一、导航功能实现a.效果图:b.后端代码c.前端代码 二、轮播图功能实现a.效果图b.后端代码c.前端代码 三、标签栏功能实现a.效果图b.后端代码c.前端代码 四、侧边栏功能实现1.整体效果图2.侧边栏功能实现a.效果图b.后端代码c.前端代码 3.侧边栏展示分类及…...

对比 UUIDv1 和 UUIDv6
UUIDv6是UUIDv1的字段兼容版本,重新排序以改善数据库局部性。UUIDv6主要在使用UUIDv1的上下文中实现。不涉及遗留UUIDv1的系统应该改用UUIDv7。 与 UUIDv1 将时间戳分割成低、中、高三个部分不同,UUIDv6 改变了这一序列,使时间戳字节从最重要…...
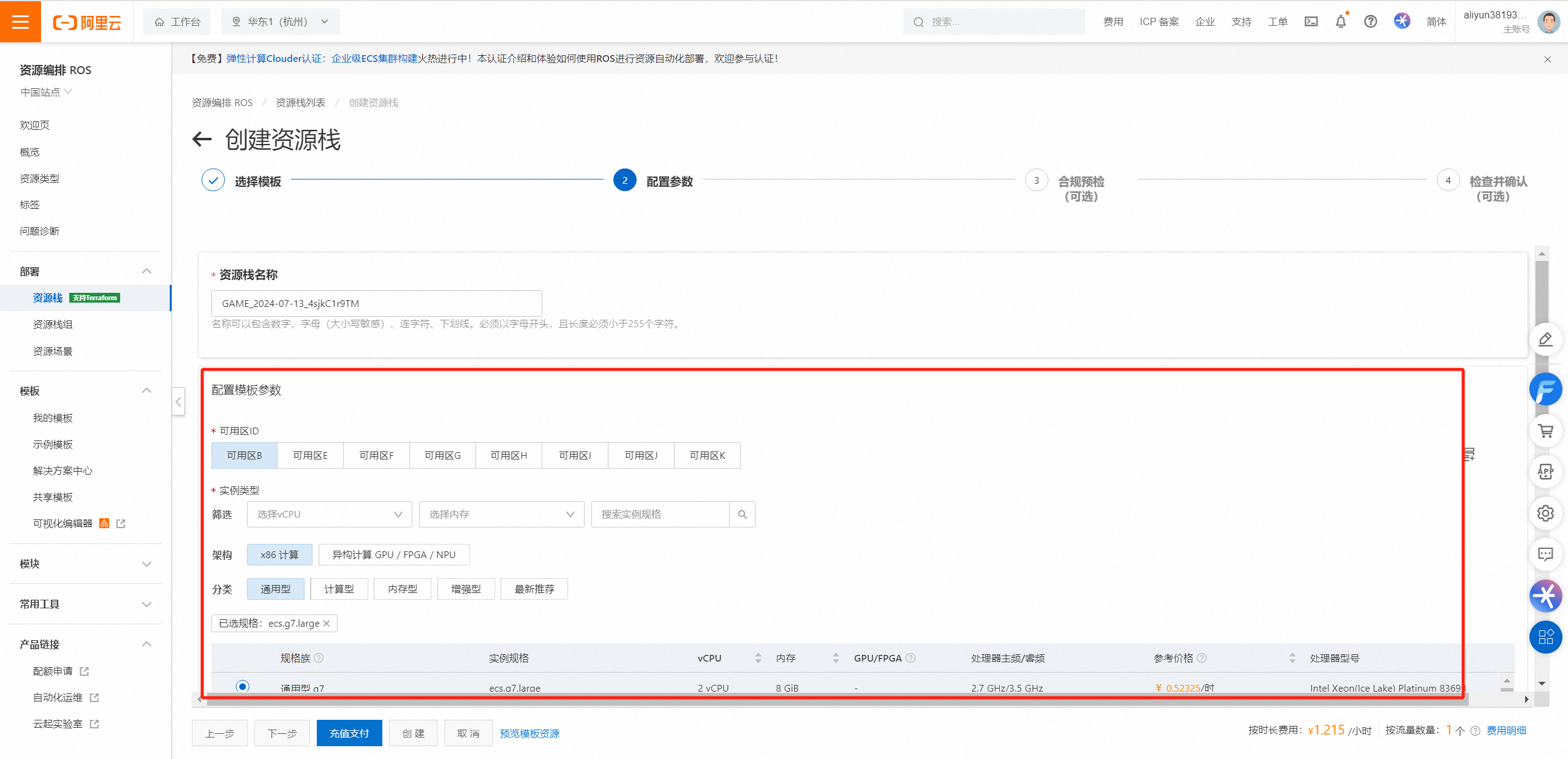
记一次饱经挫折的阿里云ROS部署经历
前言 最近在参加的几个项目测评里,我发现**“一键部署”这功能真心好用,省下了不少宝贵时间和力气,再加上看到阿里云现在有个开源上云**的活动。趁着这波热潮,今天就聊聊怎么从头开始,一步步搞定阿里云的资源编排服务…...

代码运行故障排除:PyCharm中的问题解决指南
代码运行故障排除:PyCharm中的问题解决指南 引言 PyCharm,作为一款流行的集成开发环境(IDE),提供了强大的工具来支持Python开发。然而,即使是最先进的IDE也可能遇到代码无法运行的问题。这些问题可能由多…...

css实现渐进中嵌套渐进的方法
这是我们想要的实现效果: 思路: 1.有一个底色的背景渐变 2.需要几个小的块级元素做绝对定位通过渐变filter模糊来实现 注意:这里的采用的定位方法,所以在内部的元素一律要使用绝对定位,否则会出现层级的问题&…...

JavaWeb后端学习
Web:全球局域网,万维网,能通过浏览器访问的网站 Maven Apache旗下的一个开源项目,是一款用于管理和构建Java项目的工具 作用: 依赖管理:方便快捷的管理项目以来的资源(jar包)&am…...

VUE_TypeError: Cannot convert a BigInt value to a number at Math.pow 解决方法
错误信息 TypeError: Cannot convert a BigInt value to a number at Math.pow vue 或 react package.json添加 "browserslist": {"production": ["chrome > 67","edge > 79","firefox > 68","opera >…...

Linux下mysql数据库的导入与导出以及查看端口
一:Linux下导出数据库 1、基础导出 要在Linux系统中将MySQL数据库导出,通常使用mysqldump命令行工具。以下是一个基本的命令示例,用于导出整个数据库: mysqldump -u username -p database_name > export_filename.sql 其中&a…...

Open3d入门 一文读懂三维点云
三维点云技术的发展始于20世纪60年代,随着激光雷达和三维扫描技术的进步,在建筑、考古、地理信息系统和制造等领域得到了广泛应用。20世纪90年代,随着计算机处理能力的提升,点云数据的采集和处理变得更加高效,推动了自…...
-基础介绍)
pyinstaller系列教程(一)-基础介绍
1.介绍 PyInstaller是一个用于将Python应用程序打包为独立可执行文件的工具,它支持跨平台操作,包括Windows、Linux和MacOS等操作系统。特点如下: 跨平台支持:PyInstaller可以在多个操作系统上运行,并生成相应平台的可…...

echarts图表:类目轴
category 类目轴,适用于离散的类目数据。 例如商品名称、时间等。 类目轴上的每个刻度代表一个类目,刻度之间没有量的关系,只是简单的分类。 在类目轴上,数据点会对应到相应的类目上。...

SSM贫困生申请管理系统-计算机源码84308
摘要 随着教育信息化的不断推进,越来越多的高校开始借助信息技术手段提升贫困生申请管理的效率与准确性。为此,我们设计并实现了SSM贫困生申请管理系统,旨在通过信息化手段优化贫困生申请流程,提高管理效率,为贫困生提…...

[C++]——同步异步日志系统(5)
同步异步日志系统 一、日志消息格式化设计1.1 格式化子项类的定义和实现1.2 格式化类的定义和实现 二、日志落地类设计2.1 日志落地模块功能实现与测试2.2 日志落地模块功能功能扩展 一、日志消息格式化设计 日志格式化模块的作用:对日志消息进行格式化,…...

Qt项目:基于Qt实现的网络聊天室---TCP服务器和token验证
文章目录 TCP服务器设计客户端TCP管理者ChatServerAsioIOServicePoolSession层LogicSystem总结 token验证模块完善protoStatusServer验证token客户端处理登陆回包用户管理登陆界面 本篇完成的模块是TCP服务器的设计和token验证 TCP服务器设计 客户端TCP管理者 因为聊天服务要…...

深入理解C++构造函数
目录 1.引言 2.默认构造函数 3.自定义构造函数 4.带继承关系类的构造函数 5.带多重继承关系类的构造函数 6.带虚继承关系类的构造函数 7.总结 1.引言 对于学过C的来说,构造函数是非常熟悉不过的了。但是你真正了解它吗?构造函数内部初始化变量的顺…...

J025_斗地主游戏案例开发(简版)
一、需求描述 完成斗地主游戏的案例开发。 业务:总共有54张牌; 点数:3、4、5、6、7、8、9、10、J、Q、K、A、2 花色:黑桃、红桃、方片、梅花 大小王:大王、小王 点数分别要组合4种花色,大小王各一张。…...

路径规划 | 飞蛾扑火算法求解二维栅格路径规划(Matlab)
目录 效果一览基本介绍程序设计参考文献 效果一览 基本介绍 路径规划 | 飞蛾扑火算法求解二维栅格路径规划(Matlab)。 飞蛾扑火算法(Firefly Algorithm)是一种基于自然界萤火虫行为的优化算法,在路径规划问题中也可以应…...

优化Cocos Creator 包体体积
优化Cocos Creator 包体体积 引言一、优化图片文件体积:二、优化声音文件体积:三、优化引擎代码体积:四、 优化字体字库文件大小: 引言 优化Cocos Creator项目的包体体积是一个常见且重要的任务,尤其是在移动设备和网…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...

结构化文件管理实战:实现目录自动创建与归类
手动操作容易因疲劳或疏忽导致命名错误、路径混乱等问题,进而引发后续程序异常。使用工具进行标准化操作,能有效降低出错概率。 需要快速整理大量文件的技术用户而言,这款工具提供了一种轻便高效的解决方案。程序体积仅有 156KB,…...
)
41道Django高频题整理(附答案背诵版)
解释一下 Django 和 Tornado 的关系? Django和Tornado都是Python的web框架,但它们的设计哲学和应用场景有所不同。 Django是一个高级的Python Web框架,鼓励快速开发和干净、实用的设计。它遵循MVC设计,并强调代码复用。Django有…...

用js实现常见排序算法
以下是几种常见排序算法的 JS实现,包括选择排序、冒泡排序、插入排序、快速排序和归并排序,以及每种算法的特点和复杂度分析 1. 选择排序(Selection Sort) 核心思想:每次从未排序部分选择最小元素,与未排…...

java+webstock
maven依赖 <dependency><groupId>org.java-websocket</groupId><artifactId>Java-WebSocket</artifactId><version>1.3.5</version></dependency><dependency><groupId>org.apache.tomcat.websocket</groupId&…...
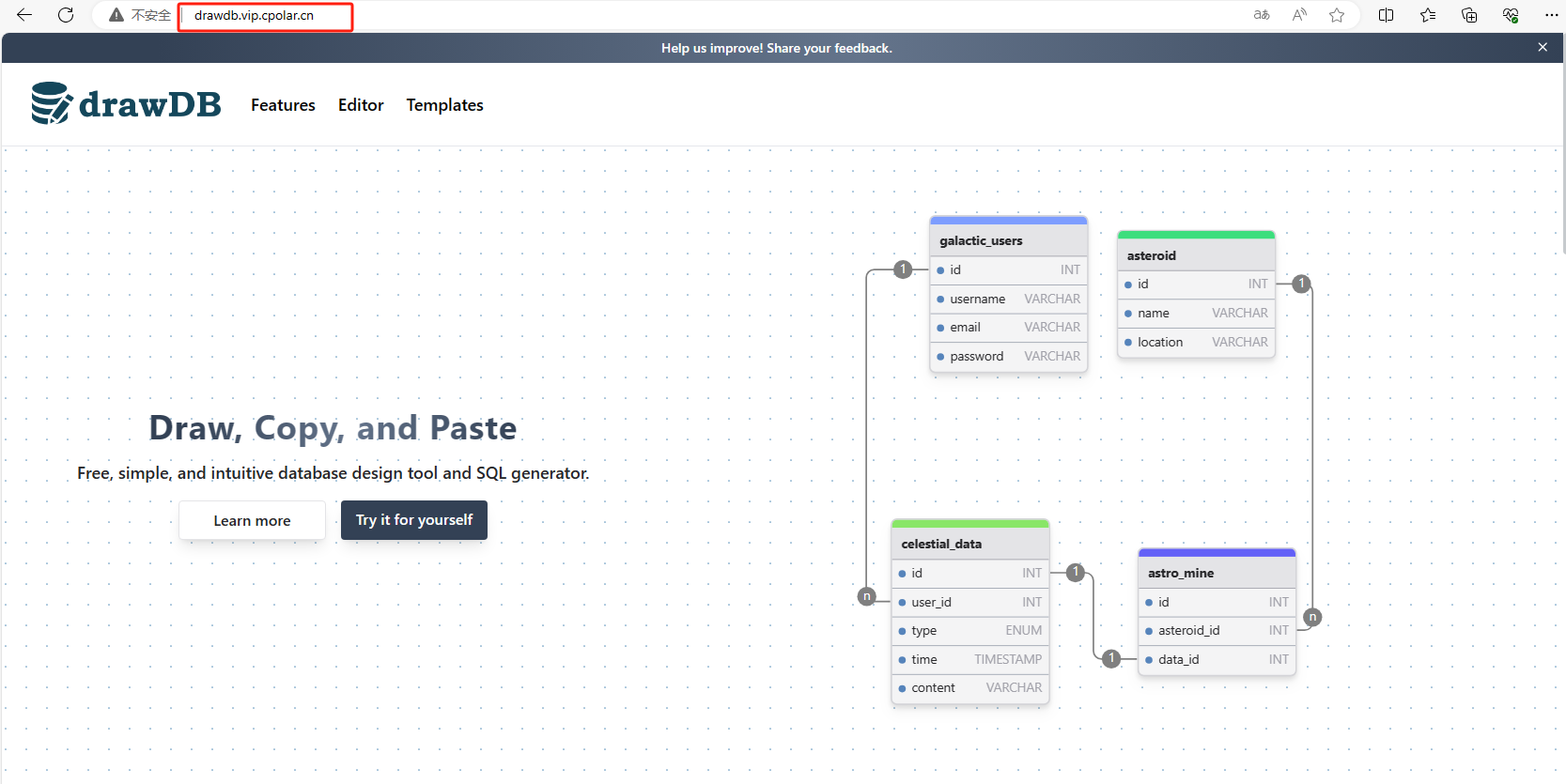
本地部署drawDB结合内网穿透技术实现数据库远程管控方案
文章目录 前言1. Windows本地部署DrawDB2. 安装Cpolar内网穿透3. 实现公网访问DrawDB4. 固定DrawDB公网地址 前言 在数字化浪潮席卷全球的背景下,数据治理能力正日益成为构建现代企业核心竞争力的关键因素。无论是全球500强企业的数据中枢系统,还是初创…...
