树的遍历方式(前中后,层序遍历,递归,迭代,Morris遍历)-----直接查询代码
目录
一.前序遍历
1.递归
2.栈迭代
3.Morris遍历
二.中序遍历
1.递归
2.栈迭代
3.Morris遍历
三.后序遍历
1.递归
2.栈迭代
3.Morris遍历
四.前中后序的统一迭代法
1.前序遍历
2.中序遍历
3.后序遍历
五.层序遍历
1.队列迭代
2.之字形层序遍历
3.锯齿形层序遍历
一.前序遍历
1.递归
ArrayList<Integer> list = new ArrayList<>();public List<Integer> preorderTraversal(TreeNode root) {preOrder(root);return list;}public void preOrder(TreeNode root) {if (root != null) {list.add(root.val);preOrder(root.left);preOrder(root.right);}}2.栈迭代
在进行使用栈进行迭代的时候,我们是先入栈右节点,然后入栈左节点,这样做是和栈的结构进行匹配的,因为栈是先进后出的结构,所以先入栈右节点,再入栈左节点,这样出栈的时候左节点才能先出栈
第一次:先入栈1,stack={1}
第二次:然后出栈1,入栈1的右节点3,stack={3},入栈1的左节点2 stack={3,2}
第三次:出栈顶元素2,stack={3},入栈2的右节点,入栈2的左节点.stack={3,5,4}
第四次,出栈顶元素4,stack={3,5},入栈4的左节点6,stack={3,5,6};
第五次:出栈顶元素6,左右结点都为空,没有元素入栈,stack={3,5};
第六次:出栈顶元素5,入栈5的右节点7,stack={3,7};
第七次:出栈顶元素7,,没有元素入栈,stack={3};
第八次,出栈顶元素3,没有元素入栈,stack={};迭代结束
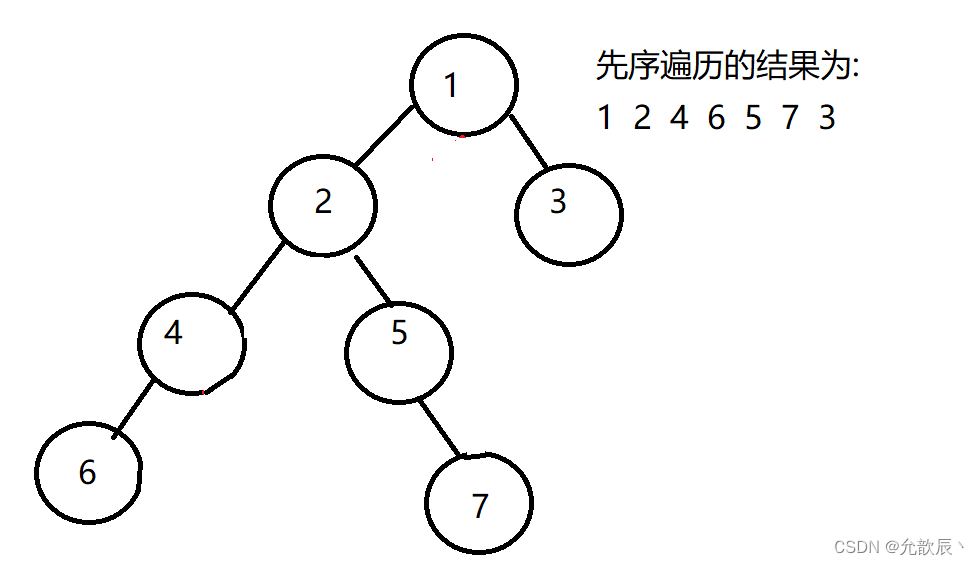
//入栈顺序为,中-->右-->左public static List<Integer> preorderTraversal(TreeNode root) {LinkedList<TreeNode> stack = new LinkedList<>();List<Integer> res = new ArrayList<>();if (root == null) {return res;}stack.push(root);while (!stack.isEmpty()) {TreeNode pop = stack.pop();res.add(pop.val);if (pop.right != null) {stack.push(pop.right);}if (pop.left != null) {stack.push(pop.left);}}return res;}3.Morris遍历
Morris遍历利用了树的线索化,时间复杂度为O(n),空间复杂度为O(1),主要节省了空间,时间复杂度还是不变,具体的分析请看这篇文章:树的前中后序的Morris遍历_允歆辰丶的博客-CSDN博客,这里直接给出代码:
public List<Integer> preorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();TreeNode curr = root;while (curr != null) {if (curr.left == null) { // 左子树为空,则输出当前节点,然后遍历右子树res.add(curr.val);//如果要求直接打印,直接输出System.out.println(curr.val);curr = curr.right;} else {// 找到当前节点的前驱节点TreeNode prev = curr.left;while (prev.right != null && prev.right != curr) {prev = prev.right;}if (prev.right == null) {res.add(curr.val);//如果要求直接打印,直接输出System.out.println(curr.val);// 将前驱节点的右子树连接到当前节点prev.right = curr;curr = curr.left;} else {// 前驱节点的右子树已经连接到当前节点,断开连接,输出当前节点,然后遍历右子树prev.right = null;curr = curr.right;}}}return res;}二.中序遍历
1.递归
ArrayList<Integer> list = new ArrayList<>();public List<Integer> inorderTraversal(TreeNode root) {infixOrder(root);return list;}public void infixOrder(TreeNode root) {if (root != null) {infixOrder(root.left);list.add(root.val);infixOrder(root.right);}}2.栈迭代
中序遍历使用栈迭代还是有一定的难度的.我们可以想一下,前序遍历先遍历的根,栈可以压入根结点,然后再出栈,而中序遍历的话,需要找到最左边的结点,然后才能出栈.这个时候我们可以设置一个cur结点,当cur结点为空的时候出栈出栈,也就是找到了最左端的结点,当cur==null的时候,进行出栈处理,然后开始访问cur的右节点.这样就可以实现中序遍历.

//入栈顺序: 左-右public static List<Integer> inorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();if (root == null) {return res;}LinkedList<TreeNode> stack = new LinkedList<>();TreeNode cur = root;while (cur != null || !stack.isEmpty()) {if (cur != null) {//cur不为空,说明没有遍历到最左端的叶子结点,也就是第一个输出的结点stack.push(cur);cur = cur.left;} else {cur = stack.pop();res.add(cur.val);cur = cur.right;}}return res;}3.Morris遍历
具体的分析请看这篇文章:树的前中后序的Morris遍历_允歆辰丶的博客-CSDN博客,这里直接给出代码:
public class InorderThreadedBinaryTree {private ThreadTreeNode pre = null;public void threadedNodes(ThreadTreeNode node) {//如果node==null,不能线索化if (node == null) {return;}//1、先线索化左子树threadedNodes(node.left);//2、线索化当前结点//处理当前结点的前驱结点//以8为例来理解//8结点的.left = null,8结点的.leftType = 1if (node.left == null) {//让当前结点的左指针指向前驱结点node.left = pre;//修改当前结点的左指针的类型,指向前驱结点node.leftType = 1;}//处理后继结点if (pre != null && pre.right == null) {//让当前结点的右指针指向当前结点pre.right = node;//修改当前结点的右指针的类型=pre.rightType = 1;}//每处理一个结点后,让当前结点是下一个结点的前驱结点pre = node;//3、线索化右子树threadedNodes(node.right);}}class ThreadTreeNode {int val;ThreadTreeNode left;//0为非线索化,1为线索化int leftType;ThreadTreeNode right;//0为非线索化,1为线索化int rightType;public ThreadTreeNode(int val) {this.val = val;}
}三.后序遍历
1.递归
ArrayList<Integer> list = new ArrayList<>();public List<Integer> postorderTraversal(TreeNode root) {postOrder(root);return list;}public void postOrder(TreeNode root) {if (root != null) {postOrder(root.left);postOrder(root.right);list.add(root.val);}}2.栈迭代
后序遍历可以思考一下前序遍历的迭代代码,后序遍历的遍历顺序为左-->右-->中,我们入栈的顺序为中-->左-->右,然后出栈的顺序为中-->右-->左,这样在最后的时候反转一下,便可以正好符合了后序遍历的顺序了.

入栈顺序:中-->左-->右 出栈顺序:中-->右-->左public List<Integer> postorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();if (root == null) {return res;}LinkedList<TreeNode> stack = new LinkedList<>();stack.push(root);while (!stack.isEmpty()) {TreeNode node = stack.pop();res.add(node.val);if (node.left != null) {stack.push(node.left);}if (node.right != null) {stack.push(node.right);}}Collections.reverse(res);return res;}3.Morris遍历
具体的分析请看这篇文章:树的前中后序的Morris遍历_允歆辰丶的博客-CSDN博客,这里直接给出代码:
public List<Integer> postorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();TreeNode dump = new TreeNode(0);//建立一个临时结点dump.left = root; //设置dump的左节点为rootTreeNode curr = dump; //当前节点为dumpwhile (curr != null) {if (curr.left == null) { // 左子树为空,则输出当前节点,然后遍历右子树curr = curr.right;} else {// 找到当前节点的前驱节点TreeNode prev = curr.left;while (prev.right != null && prev.right != curr) {prev = prev.right;}if (prev.right == null) {// 将前驱节点的右子树连接到当前节点prev.right = curr;curr = curr.left;} else {reverseAddNodes(curr.left, prev, res);// 前驱节点的右子树已经连接到当前节点,断开连接,输出当前节点,然后遍历右子树prev.right = null;curr = curr.right;}}}return res;}private void reverseAddNodes(TreeNode begin, TreeNode end, List<Integer> res) {reverseNodes(begin, end); //将begin到end的进行逆序连接TreeNode curr = end;while (true) {//将逆序连接后端begin到end添加res.add(curr.val);if (curr == begin)break;curr = curr.right;}reverseNodes(end, begin);//恢复之前的连接状态}/*** 将begin到end的进行逆序连接** @param begin* @param end*/private void reverseNodes(TreeNode begin, TreeNode end) {TreeNode prev = begin;TreeNode curr = prev.right;TreeNode post;while (prev != end) {post = curr.right;curr.right = prev;prev = curr;curr = post;}}四.前中后序的统一迭代法
1.前序遍历
我们为了同时解决访问节点(遍历节点)和处理节点(将元素放进结果集)不一致的情况,我们加入标记节点null,当出栈的结点为为null的时候,我们将再次出栈的元素加入到res结合中,
因为栈的性质:先进后出,所以在加入到栈的时候,前序要遵循右-->左-->中(做标记加入null)的顺序加入到栈,然后出栈为null结点的时候,处理结点,将元素放进结果集.
public static List<Integer> preorderTraversal(TreeNode root) {LinkedList<TreeNode> stack = new LinkedList<>();List<Integer> res = new ArrayList<>();if (root != null) {stack.push(root);}while (!stack.isEmpty()) {TreeNode node = stack.pop();if (node != null) {if (node.right != null)stack.push(node.right); // 添加右节点(空节点不入栈)if (node.left != null)stack.push(node.left); // 添加左节点(空节点不入栈)stack.push(node); // 添加中节点stack.push(null); // 中节点访问过,但是还没有处理,加入空节点做为标记。} else { // 只有遇到空节点的时候,才将下一个节点放进结果集node = stack.pop(); // 重新取出栈中元素res.add(node.val); // 加入到结果集}}return res;}2.中序遍历
因为栈的性质:先进后出,所以在加入到栈的时候,前序要遵循右-->中(做标记加入null)-->左的顺序加入到栈,然后出栈为null结点的时候,处理结点,将元素放进结果集.
public List<Integer> inorderTraversal(TreeNode root) {List<Integer> res = new LinkedList<>();LinkedList<TreeNode> stack = new LinkedList<>();if (root != null)stack.push(root);while (!stack.isEmpty()) {TreeNode node = stack.pop();if (node != null) {if (node.right != null)stack.push(node.right); // 添加右节点(空节点不入栈)stack.push(node); // 添加中节点stack.push(null); // 中节点访问过,但是还没有处理,加入空节点做为标记。if (node.left != null)stack.push(node.left); // 添加左节点(空节点不入栈)} else { // 只有遇到空节点的时候,才将下一个节点放进结果集node = stack.pop(); // 取出栈中元素res.add(node.val); // 加入到结果集}}return res;}3.后序遍历
因为栈的性质:先进后出,所以在加入到栈的时候,前序要遵循中(做标记加入null)-->右-->左的顺序加入到栈,然后出栈为null结点的时候,处理结点,将元素放进结果集.
public List<Integer> postorderTraversal(TreeNode root) {List<Integer> res = new LinkedList<>();LinkedList<TreeNode> stack = new LinkedList<>();if (root != null)stack.push(root);while (!stack.isEmpty()) {TreeNode node = stack.pop();if (node != null) {stack.push(node); // 添加中节点stack.push(null); // 中节点访问过,但是还没有处理,加入空节点做为标记。if (node.right != null)stack.push(node.right); // 添加右节点(空节点不入栈)if (node.left != null)stack.push(node.left); // 添加左节点(空节点不入栈)} else { // 只有遇到空节点的时候,才将下一个节点放进结果集node = stack.pop(); // 重新取出栈中元素res.add(node.val); // 加入到结果集}}return res;}五.层序遍历
1.队列迭代
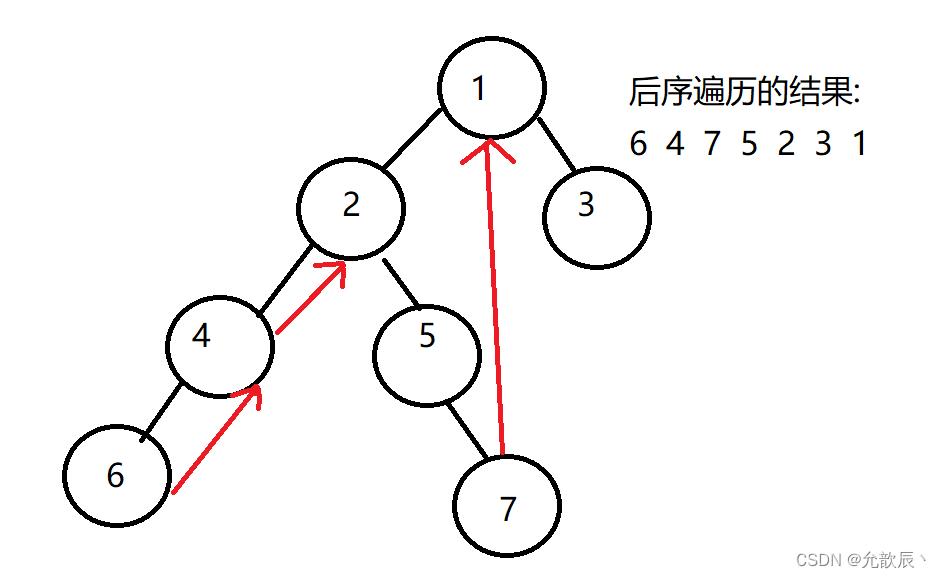
层序遍历主要是利用了队列先进后出的性质,每一次的循环次数为为当前层的结点的个数,在遍历的当前层的结点的同时,如果左右孩子不为空的话,入队当前结点的左右孩子结点,直到队列里面没有元素.例如:
第一次先根结点入队列:queue={1};
第二次:1结点出队列,然后将1的左右节点2结点和3结点入队列,queue={2,3};
第三次:2结点出队列,4和5结点入队列,3出队列,3无左右节点,queue={4,5};
第四次:4结点出队列,4的左节点入队列,5结点出队列,5的右节点入队列,queue={6,7}
第五次,6,7结点出队列,因为他们都没有左右节点,因此queue=null,遍历结束
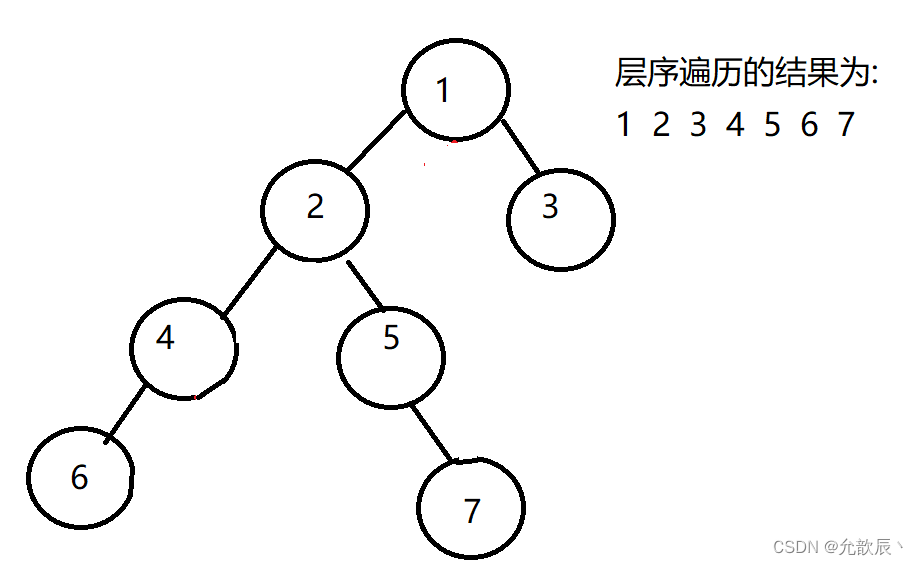
public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> list = new ArrayList<>();if (root == null)return list;LinkedList<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {int size = queue.size();List<Integer> res = new ArrayList<>();for (int i = 0; i < size; ++i) {TreeNode node = queue.poll();res.add(node.val);if (node.left != null)queue.offer(node.left);if (node.right != null)queue.offer(node.right);}list.add(res);}return list;}2.之字形层序遍历
用两个栈实现之字形(Z字形)打印,如下图的遍历顺序,一个栈是正向存储每层的元素,一个栈逆向存储每层的元素,当然也可以使用一个队列完成
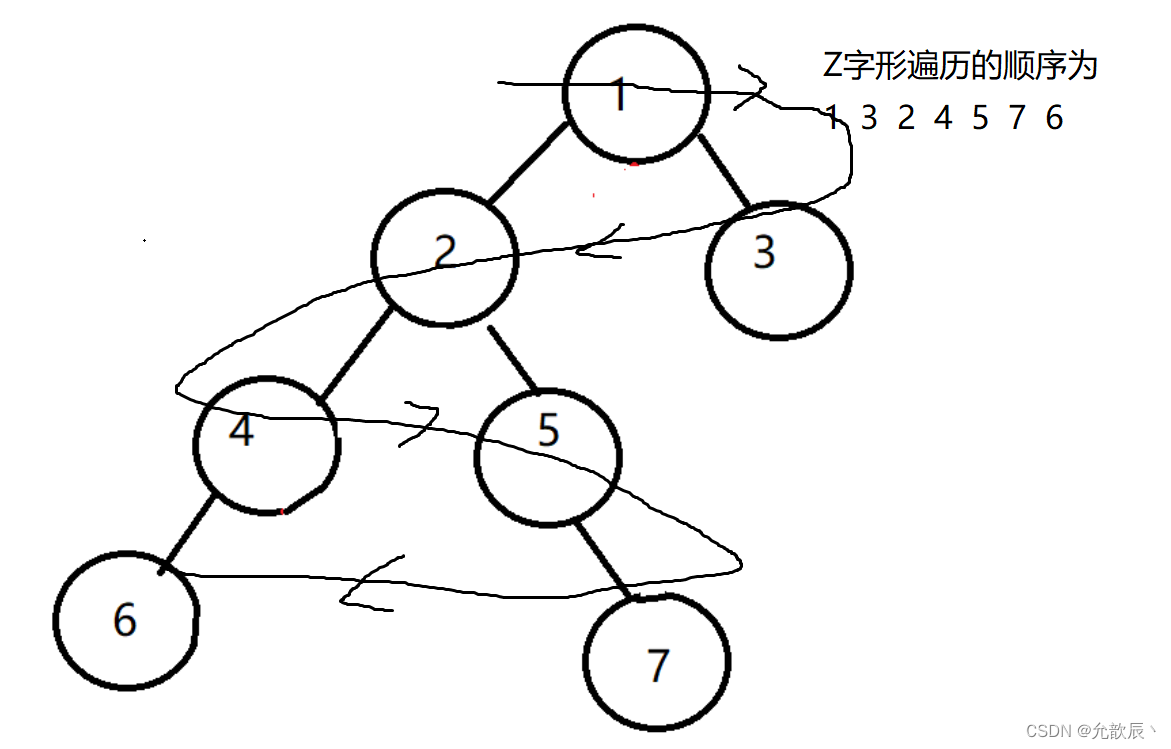
public static List<Integer> zprintf(TreeNode root) {LinkedList<TreeNode> stack1 = new LinkedList<>();LinkedList<TreeNode> stack2 = new LinkedList<>();ArrayList<Integer> list = new ArrayList<>();boolean flag = false;if (root != null)stack1.push(root);while (!stack2.isEmpty() || !stack1.isEmpty()) {if (!flag) {TreeNode node = stack1.pop();list.add(node.val);if (node.left != null)stack2.push(node.left);if (node.right != null)stack2.push(node.right);if (stack1.isEmpty()) {flag = true;}} else {TreeNode node = stack2.pop();list.add(node.val);if (node.right != null)stack1.push(node.right);if (node.left != null)stack1.push(node.left);if (stack2.isEmpty()) {flag = false;}}}return list;}3.锯齿形层序遍历
力扣:力扣
-
如果从左至右,我们每次将被遍历到的元素插入至双端队列的末尾。
-
如果从右至左,我们每次将被遍历到的元素插入至双端队列的头部。
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {List<List<Integer>> ans = new ArrayList<>();LinkedList<TreeNode> queue = new LinkedList<>();boolean isOrderLeft = true;if (root == null)return ans;queue.push(root);while (!queue.isEmpty()) {LinkedList<Integer> levelList = new LinkedList<>();int size = queue.size();for (int i = 0; i < size; ++i) {TreeNode node = queue.poll();if(isOrderLeft){levelList.offer(node.val);}else {levelList.push(node.val);}if (node.left != null) {queue.offer(node.left);}if (node.right != null) {queue.offer(node.right);}}ans.add(levelList);isOrderLeft = !isOrderLeft;}return ans;}相关文章:

树的遍历方式(前中后,层序遍历,递归,迭代,Morris遍历)-----直接查询代码
目录 一.前序遍历 1.递归 2.栈迭代 3.Morris遍历 二.中序遍历 1.递归 2.栈迭代 3.Morris遍历 三.后序遍历 1.递归 2.栈迭代 3.Morris遍历 四.前中后序的统一迭代法 1.前序遍历 2.中序遍历 3.后序遍历 五.层序遍历 1.队列迭代 2.之字形层序遍历 3.锯齿形层序…...
Docker Registry部署镜像私有仓库及鉴权认证
文章目录一、Docker Registry是什么?二、Docker Registry部署私有仓库2.1、Docker Registry安装2.2、Docker Registry配置2.3、启动Docker Registry2.4、Docker客户端配置2.5、向Docker Registry上传和下载镜像三、Docker Registry鉴权和认证3.1、基本认证3.2、Bear…...
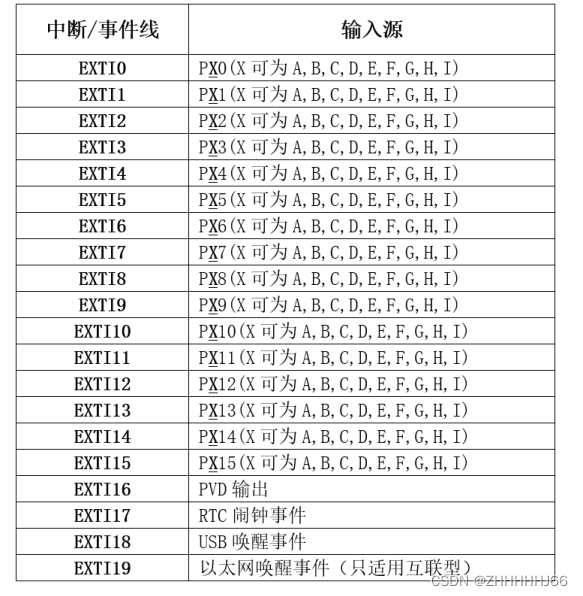
stm32外设-中断详解
0. 写在最前 本栏目笔记都是基于stm32F10x 1. 中断是啥? 什么是中断:CPU在处理某一事件A时,发生的另外某一事件B请求CPU去处理(产生了中断),随后CPU暂时中断当前正在执行的任务,去对事件B进行处…...
第十四届蓝桥杯三月真题刷题训练——第 13 天
目录 第 1 题:特殊日期 问题描述 答案提交 运行限制 代码: 思路: 第 2 题:重合次数 问题描述 答案提交 运行限制 代码: 第 3 题:左移右移 问题描述 输入格式 输出格式 样例输入 样例输出…...

webgl_gpgpu_birds 样例分析
webgl_gpgpu_birds 是一个 three.js 的官方样例,这个例子模拟了鸟群的运动,是一个群组动画,并且动画的帧率也很高;鸟群的运动很自然,非常值得研究。类似的群组动画还有鱼群,boid是‘类鸟群’的英文 大概两…...

以业务行为驱动的反入侵安全能力建设
0x0 背景 最近听到一些甲方安全领域的专家分享了部分安全建设的经验,对安全运营下的反入侵技术能力建设有了些新的看法,依靠单个/多个异构的安全产品的关联能力形成的安全中台并不能在实际的攻防对抗当中占据主动地位,且很容易达到一个天花板…...

Unity3d C#使用DOTween插件的Sequence实现系列动画OnComplete无效和颜色设置无效的问题记录
前言 最近在弄一个文字动画效果的动画,使用了DOTween插件的Sequence来实现,主要就是对一个Text进行的文字打字、缩放和颜色设置等动画,功能是先对Text实现打字的动画,打字完成后,延时几秒对文字进行缩小、颜色变淡&am…...

【蓝桥杯-筑基篇】排序算法
🍓系列专栏:蓝桥杯 🍉个人主页:个人主页 目录 前言: 一、冒泡排序 二、选择排序 三、插入排序 四、图书推荐 前言: 算法工具推荐: 还在为数据结构发愁吗?这款可视化工具,帮助你更好的了解…...
编辑器进化 VSCode + Vim
本文作者为 360 奇舞团前端工程师VSCode 是一款非常流行的代码编辑器。它支持多种编程语言,拥有丰富的插件和调试功能,不论是处理前端工程还是后端工程,VSCode 都能提供给开发者优秀的用户体验。鉴于 VSCode 超高的流行度,我会默认…...

LearnOpenGL-高级OpenGL-6.天空盒
本人刚学OpenGL不久且自学,文中定有代码、术语等错误,欢迎指正 我写的项目地址:https://github.com/liujianjie/LearnOpenGLProject 文章目录天空盒介绍如何采样OpenGL纹理目标例子0:天空盒效果环境映射反射例子1:Cube…...

Printk打印内核日志
一、背景 Linux 内核中提供了内核日志打印的工具printk。它的使用方式C语言中的printf是类似的。接下来我们介绍一下printk的使用方式。本文以打印Binder中的日志为例,进行演示。 printk的方法声明和日志级别binder驱动中增加 打印代码android系统中查看日志信息 …...
界面控件DevExpress WPF 202计划发布的新功能合集
DevExpress WPF拥有120个控件和库,将帮助您交付满足甚至超出企业需求的高性能业务应用程序。通过DevExpress WPF能创建有着强大互动功能的XAML基础应用程序,这些应用程序专注于当代客户的需求和构建未来新一代支持触摸的解决方案。本文将介绍今年DevExpr…...

Spring Cloud Alibaba 微服务2,注册中心演变 + Nacos注册中心与配置中心
目录专栏导读一、什么是Nacos?二、注册中心演变及其设计思想1、RestTemplate调用远程服务2、通过Nginx维护服务列表(upStream)3、通过Nacos实现注册中心4、心跳版Nacos三、Nacos Discovery四、Nacos核心功能1、服务注册2、服务心跳3、服务同步…...
Navicat 图形化界面工具
Navicat 介绍 Navicat是一套可创建多个连接的数据库管理工具,用以方便管理 MySQL、Oracle、SQL Server等不同类型的数据库 目录 Navicat 介绍 Navicat 下载 Navicat 安装 Navicat 使用 Navicat连接MySQL数据库 Navicat创建数据库和表 Navicat 下载 1、点击这…...
2023年网络安全比赛--attack(新)数据包分析中职组(超详细)
一、竞赛时间 180分钟 共计3小时 任务环境说明: 1 分析attack.pcapng数据包文件,通过分析数据包attack.pcapng找出恶意用户第一次访问HTTP服务的数据包是第几号,将该号数作为Flag值提交; 2.继续查看数据包文件attack.pcapng,分析出恶意用户扫描了哪些端口,将全部的端口号…...
)
C语言之extern(七十)
extern同一个文件:修饰变量声明#include <stdio.h>int add(){extern int x,y;return x y; }int main(){printf("%d\n", add()); }int x 10; int y 20;extern文件之间:修饰函数声明<1>.add.cint sum(){extern int x ;extern in…...
树的前中后序的Morris遍历
目录 一.Morris遍历 1.什么是Morris遍历 2.基本思想 3.Morris遍历的优点和缺点 4.知识回顾----二叉树的线索化 二.中序Morris遍历 1.中序Morris遍历的分析 2.中序Morris遍历的思路 3.具体的代码实现 三.前序Morris遍历 1.前序Morris遍历的思路 2.具体的代码实现 四…...
到底什么是线程?线程与进程有哪些区别?
上一篇文章我们讲述了什么是进程,进程的基本调度 http://t.csdn.cn/ybiwThttp://t.csdn.cn/ybiwT 那么本篇文章我们将了解一下什么是线程?线程与进程有哪些区别?线程应该怎么去编程? 目录 http://t.csdn.cn/ybiwThttp://t.csdn…...

你真的知道如何系统高效地学习数据结构与算法吗?
文章目录前言:什么是数据结构?什么是算法?学习这个算法需要什么基础?学习的重点在什么地方?一些可以让你事半功倍的学习技巧1.边学边练,适度刷题2.多问、多思考、多互动3.打怪升级学习法4.知识需要沉淀&…...

Linux操作系统基础的常用命令
1,Linux简介Linux是一种自由和开放源码的操作系统,存在着许多不同的Linux版本,但它们都使用了Linux内核。Linux可安装在各种计算机硬件设备中,比如手机、平板电脑、路由器、台式计算机。1.1Linux介绍Linux出现于1991年,…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...
