AI算法18-最小角回归算法Least Angle Regression | LARS
最小角回归算法简介
最小角回归(Least Angle Regression, LAR)是一种用于回归分析的统计方法,它在某些方面类似于最小二乘回归,但提供了一些额外的优点。最小角回归由Bradley Efron等人提出,主要用于处理具有高度相关性的特征集。
最小角回归算法的核心思想是逐步添加特征到模型中,每次添加与当前残差相关性最大的特征。这个过程通过最小化角(即特征与残差之间的夹角)来实现,从而确保模型的稀疏性。这使得LAR算法在处理具有多重共线性的数据集时特别有用。
我们直接看最基本的LAR算法,假设有N个样本,自变量是p维的:
- 先对
做标准化处理,使得每个predictor(
的每列)满足
,
。我们先假设回归模型中只有截距项,则
,记残差
,而其他的系数
。
- 找出与
相关性最大的
,加入active set;
- 将
从0逐步向LS系数
变动,直到有另一个
,它与
的相关系数绝对值,和
与
的相关系数绝对值一样大;
- 将
和
同时向二者的联合LS系数变动,直到再出现下一个
,它与
的相关系数满足上一步的条件;
- 重复上述过程,
步后,就得到完整的LS解。

最小角回归算法主要解决的问题
- 多重共线性:数据集中的特征之间存在高度相关性,这可能导致最小二乘回归模型的参数估计不稳定。
- 特征选择:在特征数量多于样本数量的情况下,需要选择对模型预测最有帮助的特征子集。
- 稀疏模型:需要一个具有较少非零系数的模型,以便于解释和减少模型复杂度。
- 稳健性:在数据中存在噪声或异常值时,需要一个对这些情况不敏感的模型。
- 预测准确性:在保持模型简洁的同时,追求较高的预测准确性。
- 线性回归问题:LAR可以应用于标准的线性回归问题,即预测一个连续的响应变量。
- 逻辑回归问题:通过适当的修改,LAR也可以应用于分类问题,如逻辑回归。
- 多元回归问题:LAR可以处理多个响应变量的回归问题,即多元线性回归。
- 正则化问题:LAR提供了一种正则化方法,可以控制模型的复杂度,防止过拟合。
- 交叉验证问题:在模型选择过程中,LAR可以用于交叉验证,以选择最佳的模型复杂度。
- 模型解释性:由于LAR倾向于产生稀疏模型,因此它可以提高模型的可解释性。
- 大规模数据集:LAR算法适用于大规模数据集,尤其是当数据集中的特征数量非常多时。
最小角回归算法基本思想和理论基础
最小角回归算法基本思想
- 稀疏模型:LAR的目标是构建一个稀疏的回归模型,即模型中只有少数几个特征具有非零系数,这有助于提高模型的可解释性和降低过拟合的风险。
- 逐步添加特征:LAR通过逐步添加特征到模型中来构建。在每一步中,算法选择当前与残差相关性最大的特征加入模型,这个过程是迭代的。
- 最小化角:LAR的核心思想是最小化特征向量与残差向量之间的夹角。这个夹角的大小代表了特征对当前残差解释能力的大小。选择夹角最小的特征意味着选择了最能解释当前残差的特征。
- 正则化:LAR通过正则化项控制模型的复杂度,类似于LASSO算法,但LAR的正则化是通过最小化角来实现的,而不是直接对系数的大小进行惩罚。
- 数据驱动:LAR算法是数据驱动的,它根据数据本身的特性来选择特征,而不是依赖于预先设定的模型假设。
- 稳健性:由于LAR算法在每一步都考虑了特征与残差的相关性,它对数据中的噪声和异常值具有一定的稳健性。
- 快速计算:LAR算法利用了数据的稀疏性质和快速的更新规则,使得算法在计算上相对高效。
- 灵活性:LAR算法可以应用于不同类型的回归问题,包括线性回归、逻辑回归等,并且可以处理大规模数据集。
- 交叉验证:LAR算法可以结合交叉验证等方法来选择最佳的正则化参数,实现模型的自动选择。
- 模型解释性:由于LAR倾向于产生稀疏模型,它提高了模型的可解释性,使得模型更容易被理解和应用。
最小角回归算法理论基础
- 线性回归问题:LAR算法是针对线性回归问题设计的,它通过逐步添加特征的方式进行特征选择和回归系数的计算 。
- 特征向量分解:LAR算法的核心在于将回归目标向量分解为若干组特征向量的线性组合,关键在于选择正确的特征向量分解顺序和分解系数 。
- 前向选择算法:LAR算法与前向选择算法(Forward Selection)有关,前向选择算法是一种贪婪算法,通过选择与目标向量相关度最高的特征向量进行分解 。
- 前向梯度算法:LAR算法也与前向梯度算法(Forward Stagewise)有关,该算法通过小步试错的方式进行特征向量的选择和分解 。
- 最小化角:LAR算法通过最小化特征向量与残差向量之间的夹角来进行特征选择,这种方法结合了前向选择算法的快速性和前向梯度算法的准确性 。
- 正则化方法:LAR算法是一种正则化方法,它可以求解Lasso回归问题,并且可以得到Lasso解的路径 。
- 算法性质:LAR算法保持最小角的性质,即在分解过程中,每个predictor与残差向量的相关系数会同比例地减少 。
- 模型的求解:LAR算法通过逐步更新残差向量和逐步调整回归系数,直到满足终止条件,如残差向量足够小或所有变量都已使用完毕 。
- 稳定性和灵活性:LAR算法具有很好的稳定性和灵活性,适用于特征维度远高于样本数的情况,并且可以容易地修改以适应其他估算器,如LASSO 。
- 算法效率:LAR算法在计算上非常有效,特别是当特征维度远大于样本数量时,它的计算速度几乎和前向选择算法一样快
最小角回归算法步骤
1.初始化:
将所有特征的系数初始化为零。
计算初始残差向量,即响应向量与所有特征系数为零时的残差。
2.标准化特征:
为了确保算法不受特征尺度的影响,对所有特征向量进行标准化处理。
3.构建活动集:
初始化一个活动集(active set),包含与当前残差向量相关性最大的特征。
4.计算相关性:
对于每个特征,计算它与当前残差向量的相关系数。
5.选择特征:
选择与当前残差向量相关性最大的特征,将其添加到活动集中。
6.更新系数:
对活动集中的每个特征,逐步更新其系数,直到另一个特征的相关性与当前特征相同。
7.调整系数:
当两个或多个特征与残差向量的相关性相等时,同时更新这些特征的系数,直到它们的相关性不再相等。
8.更新残差:
使用当前的系数和特征向量来更新残差向量。
9.检查终止条件:
如果残差向量的范数低于某个阈值,或者已经没有更多的特征可以添加到模型中,则算法终止。
10.重复迭代:
重复步骤4到9,直到满足终止条件。
11.输出结果:
最终,算法输出模型的系数向量,这些系数代表了特征对响应变量的影响。
最小角回归算法推导
保持最小角
我们先来看LS估计量的一个性质:若每个predictor与的相关系的数绝对值相等,从此时开始,将所有系数的估计值同步地从0移向LS估计量,在这个过程中,每个predictor与残差向量的相关系数会同比例地减少。
假设我们标准化了每个predictor和,使他们均值为0,标准差为1。在这里的设定中,对于任意
,都有
,其中
为常数。LS估计量
,当我们将系数从0向
移动了
比例时,记拟合值为
。
另外,记为只有第
个元素为1、其他元素均为0的
维向量,则
,再记,记投影矩阵
。
这里的问题是,在变大过程中,每一个
与新的残差的相关系数,是否始终保持相等?且是否会减小?
由于,即内积与
无关。再由
可知
。
相关系数的绝对值

因此,任意predictor与当前残差的相关系数绝对值,会随着的增加,同比例地减小,并且
。
现在,我们再回顾一下LAR的过程。在第步开始时,将所有active set中的predictor的集合记为
,此时在上一步估计完成的系数为
,它是维且每个维度都非零的向量,记此时残差为
,用
对
做回归后系数为
,拟合值
。另外,我们知道
,而一个predictor加入
的条件就是它与当前
的相关系数的绝对值等于
中的predictor与当前
的相关系数的绝对值,所以
向量的每个维度的绝对值都相等,也即
′的每个维度的绝对值都相等,
就是与各个
中的predictor的角度都相等的向量,且与它们的角度是最小的,而
也是下一步系数要更新的方向,这也是“最小角回归”名称的由来。
参数更新
那么,在这个过程中,是否需要每次都逐步小幅增加,再检查有没有其他predictor与残差的相关系数绝对值?有没有快速的计算的方法?答案是有的。
在第步的开始,
中有
个元素,我们记
,其中
,并记
,此时的active set其实就是
。在这里,我们将
做个修改,记
,再令
。
此时更新方向为,并取
。更新的规则为
。因此,任一predictor,与当前残差的内积就为
,而对于
,有
。
对于,如果要使与当前残差的相关系数绝对值,与在
中的predictor与当前残差的相关系数绝对值相等,也即它们的内积的绝对值相等,必须要满足
。问题转化为了求解使它们相等的
,并对于所有的
,最小
的即为最后的更新步长。
由于,因此只需考虑
与
的大小关系即可。最后解为

注意到

因此,当时,除非
即
,否则必有
。反之,当
时,除非
即
,否则必有
。综上所述,上面的解可以写为

其中表示只对其中正的元素有效,而丢弃负的元素。
最小角回归算法代码实现
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Lars
import matplotlib.pyplot as plt# 示例数据生成
np.random.seed(0)
X = 2.5 - 1.5 * np.random.randn(100, 1)
y = 1 + 2 * X + 0.5 * np.random.randn(100, 1)# 添加截距项
X = np.hstack([np.ones((100, 1)), X])# 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 创建LARS模型实例
lars = Lars()# 拟合模型
lars.fit(X_scaled, y)# 打印系数
print("Coefficients:", lars.coef_)# 绘制系数路径
plt.plot(lars.coef_, drawstyle="steps")
plt.xlabel("Variables")
plt.ylabel("Coefficient Value")
plt.title("Coefficient Path of LARS")
plt.show()最小角回归算法具有以下优缺点
优点:
- 高维数据处理:LAR算法特别适合于特征维度 n 远高于样本数 m 的情况,能够有效处理高维数据 。
- 计算效率:算法的最坏计算复杂度与最小二乘法类似,但计算速度几乎与前向选择算法一样快 。
- 系数路径:LAR算法可以产生分段线性结果的完整路径,这在模型的交叉验证中非常有用 。
- 稳定性:如果两个变量对响应有几乎相等的联系,则LAR算法会给予它们相似的系数增长率,这与我们的直觉判断一致,且更加稳定 。
- 灵活性:LAR算法容易修改并为其他估算器生成解,例如可以用于求解Lasso回归问题 。
缺点:
- 对噪声敏感:由于LAR算法的迭代方向是根据目标残差而定,因此该算法对样本的噪声非常敏感 。
- 实现复杂性:尽管算法本身在理论上具有吸引力,但在实际实现时可能较为复杂,特别是对于非专家用户 。
最小角回归算法的应用场景
- 高维数据回归问题:LAR算法特别适用于处理特征数量多于样本数量的高维数据集,能够有效地进行变量选择和回归分析 。
- 生物信息学:在生物信息学领域,LAR可以用于处理基因表达数据,识别重要的生物标记 。
- 金融分析:LAR在量化分析和风险预测中应用,帮助分析金融数据和预测市场趋势 。
- 信号处理:在信号处理领域,LAR可以用于信号恢复和噪声减少,提高信号的质量 。
- 大规模数据分析:对于特征众多的数据集,LAR进行有效的变量选择和数据压缩,简化模型并提高解释能力 。
- 特征选择:LAR算法提供了一种高效的特征选择方式,尤其在变量个数远大于样本数的情况下,能够快速识别出重要的特征 。
- 稳健性分析:LAR算法在变量选择上表现出较高的稳定性,对于高度相关的变量,提供了更加稳健的解决方案 。
- 教育和研究:在教育和研究领域,LAR算法被用于教学和研究项目,帮助学生和研究人员理解高维数据的回归分析方法 。
模型优化:通过使用网格搜索(GridSearchCV)和交叉验证的方法来精细调整LAR模型的参数,期望获得最佳的模型性能 。
相关文章:
AI算法18-最小角回归算法Least Angle Regression | LARS
最小角回归算法简介 最小角回归(Least Angle Regression, LAR)是一种用于回归分析的统计方法,它在某些方面类似于最小二乘回归,但提供了一些额外的优点。最小角回归由Bradley Efron等人提出,主要用于处理具有…...

wordpress 调用另外一个网站的内容 按指定关键词调用
要在WordPress中调用另一个网站的内容并根据指定关键词进行筛选,你可以使用以下代码。这段代码使用了WordPress内置的wp_remote_get函数来获取远程网站的内容,然后使用PHP的DOMDocument和DOMXPath类来解析HTML并筛选出包含指定关键词的内容。 首先&…...

kotlin数据类型
人不走空 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌赋:斯是陋室,惟吾德馨 Kotlin基本数值类型 基本数据类型包括 Byte、Short、Int、Long、Float、Double 整数类型 类型位宽最小值最大…...

[GWCTF 2019]babyvm
第一次接触VM逆向 先粘一下对我很有帮助的两篇佬的博客 系统学习vm虚拟机逆向_vmp 虚拟机代码逆向-CSDN博客 这篇去学习vm逆向到底是什么 我的浅显理解啊,就是和汇编的定义差不多,规定一个函数,用什么其他的名字 然后这道题 [GWCTF 2019]babyvm 详解 (vm逆向 …...

PyTorch论文
2019-12 PyTorch: An Imperative Style, High-Performance Deep Learning Library 设计迎合4大趋势: 1. array-based (Tensor) 2. GPU加速 3. 自动求导 (Auto Differentiation) 4. 拥抱Python生态 4大设计原则: 1. 使用算法和数据开发者熟悉的Python做编…...
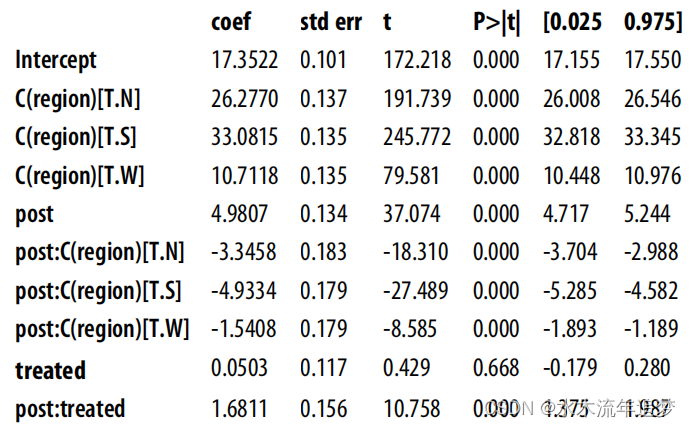
【Python实战因果推断】37_双重差分8
目录 Diff-in-Diff with Covariates Diff-in-Diff with Covariates 您需要学习的 DID 的另一个变量是如何在模型中包含干预前协变量。这在您怀疑平行趋势不成立,但条件平行趋势成立的情况下非常有用: 考虑这种情况:您拥有与之前相同的营销数…...

【python学习】第三方库之matplotlib的定义、功能、使用场景和代码示例(线图、直方图、散点图)
引言 Matplotlib 是一个 Python 的 2D 绘图库,它可以在各种平台上以各种硬拷贝格式和交互环境生成具有出版品质的图形。通过 Matplotlib,开发者可以仅需要几行代码,便可以生成绘图、直方图、功率谱、条形图、错误图、散点图等 Matplotlib 是 …...

MySQL(3)表的操作
目录 1. 表的操作; 2. 数据类型; 1. 表的操作: 1.1 创建表: 语法: create table 表名( 属性 类型 [comment ], 属性 类型 [comment ], 属性 类型 ) character set 字符集 collate 校验集 engine 存储引擎; 前面博客提到: MyISAM和InoDB这两个比较重要. 1.2 查看表…...

SQL GROUPING运算符详解
在大数据开发中,我们经常需要对数据进行分组和汇总分析。 目录 1. GROUPING运算符概念2. 语法和用法3. 实际应用示例4. GROUPING运算符的优势5. 高级应用场景5.1 与CASE语句结合使用5.2 多维数据分析 6. 性能考虑和优化技巧7. GROUPING运算符的局限性8. 最佳实践9. GROUPING与其…...

在VS2017下FFmpeg+SDL编写最简单的视频播放器
1.下载ShiftMediaProject/FFmpeg 2.下载SDL2 3.新建VC控制台应用 3.配置include和lib 4.把FFmpeg和SDL的dll 复制到工程Debug目录下,并设置调试命令 5.复制一下mp4视频到工程Debug目录下(复制一份到*.vcxproj同一目录,用于调试) 6…...

LogViewer v2.x更新
logvewer 介绍 logviewer 是一个可以方便开发人员通过浏览器查看和下载远程服务器集群日志,使用ssh方式管理远程tomcat、jar包等应用,节省服务器资源。大家可以下载体验,请勿用于生产环境。欢迎提出意见或建议。 解决的问题 一般情况下公司…...

detection_segmentation
目标检测和实例分割(OBJECT_DETECTION AND INSTANCE SEGMENTATION) 文章目录 目标检测和实例分割(OBJECT_DETECTION AND INSTANCE SEGMENTATION)一. 计算机视觉(AI VISION)1. 图像分类2. 目标检测与定位3. 语义分割和实例分割目标检测算法可以分为两大类: R-CNN生成…...

0基础学python-13:古希腊掌管时间的模块——datetime和time
目录 前言 datetime模块 一、datetime 类 1.创建 datetime 对象 2.获取日期时间的各个部分 3.格式化日期时间为字符串 4.解析字符串为 datetime 对象 二、timedelta 类 1.创建 timedelta 对象 datetime注意事项 time模块 1.获取当前时间戳 2.获取当前时间的结构化表…...

棒球特长生升学具有其独特的优势和劣势·棒球6号位
棒球特长生升学具有其独特的优势和劣势,以下是对这两方面的详细分析: 获得更好的教育资源: 棒球特长生有机会通过棒球特长招生计划进入更好的学校。这些学校往往拥有更优质的教育资源,包括师资力量、教学设施、课程设置等&#…...

搜维尔科技:Xsens DOT 可穿戴传感器介绍及示例应用演示
Xsens DOT可穿戴传感器介绍及示例应用演示 搜维尔科技:Xsens DOT 可穿戴传感器介绍及示例应用演示...

数据分析案例-2024 年热门动漫数据集可视化分析
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...

C#小结:未能找到类型或命名空间名“xxx”(是否缺少 using 指令或程序集引用?)
方案一:移除类库这些失效的引用,下载对应版本的dll(如有则不需要重复下载),重新添加引用 方案二:类库右键属性-调整目标框架版本(一般是降低版本) 方案三:调整类库编译顺…...

STM32智能无人机控制系统教程
目录 引言环境准备智能无人机控制系统基础代码实现:实现智能无人机控制系统 4.1 数据采集模块 4.2 数据处理与控制算法 4.3 通信与网络系统实现 4.4 用户界面与数据可视化应用场景:无人机管理与优化问题解决方案与优化收尾与总结 1. 引言 智能无人机控…...

从 QWebEnginePage 打印文档
QWebEnginePage 是 Qt WebEngine 模块中的一个类,它提供了用于处理网页内容的接口。如果你想要打印 QWebEnginePage 中的内容,你可以使用 QPrinter 和 QPrintDialog 类来实现。 项目配置了 Qt WebEngine 模块,并且在你的.pro文件中包含了相应…...

初识Docker及管理Docker
Docker部署 初识DockerDocker是什么Docker的核心概念镜像容器仓库 容器优点容器在内核中支持2种重要技术:Docker容器与虚拟机的区别 安装Docker源码安装yum安装检查Docker Docker 镜像操作配置镜像加速器(阿里系)搜索镜像获取镜像查看镜像信息…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...
