C/C++每日一练(20230314)

目录
1. 移动数组中的元素
2. 搜索二维矩阵
3. 三角形最小路径和
🌟 每日一练刷题专栏 🌟
Golang 每日一练 专栏
C/C++ 每日一练 专栏
Python 每日一练 专栏
Java 每日一练 专栏
1. 移动数组中的元素
将一维数组中的元素循环左移 k 个位置
输入:
第 1 行是一维数组元素的个数 n (数组大小)
第 2 行是一个整数 k , 表示移动的位置
下面 n 行为数组的元素个数
输出:
输出 n 行,表示移动后的数字
代码:
#include <stdio.h>
#define N 10000
int main()
{int k, a[N], b[N], n, t, w, i;scanf("%d", &n);scanf("%d", &k);for (i = 0; i < n; i++)scanf("%d", &a[i]);for (i = 0; i < k % n; i++)b[i] = a[i];for (i = 0; i < n; i++){if (i < n - k % n)a[i] = a[i + k % n];elsea[i] = b[i - n + k % n];}for (i = 0; i < n; i++)printf("%d\n", a[i]);return 0;
}输入输出:
5
3
1 2 3 4 5
4
5
1
2
3
2. 搜索二维矩阵
编写一个高效的算法来判断 m x n 矩阵中,是否存在一个目标值。该矩阵具有如下特性:
- 每行中的整数从左到右按升序排列。
- 每行的第一个整数大于前一行的最后一个整数。
示例 1:
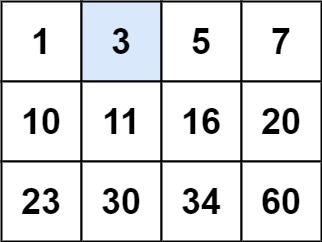
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3 输出:true
示例 2:
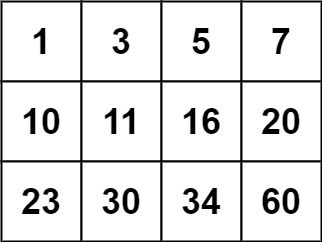
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13 输出:false
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 100-10^4 <= matrix[i][j], target <= 10^4
代码:
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>static int binary_search(int *nums, int len, int target)
{int low = -1;int high = len;while (low + 1 < high){int mid = low + (high - low) / 2;if (target > nums[mid]){low = mid;}else{high = mid;}}if (high == len || nums[high] != target){return -high - 1;}else{return high;}
}static bool searchMatrix(int **matrix, int matrixRowSize, int matrixColSize, int target)
{if (matrixRowSize == 0 || matrixColSize == 0){return false;}if (target < matrix[0][0] || target > matrix[matrixRowSize - 1][matrixColSize - 1]){return false;}int row = 0;int *nums = NULL;if (matrixRowSize > 0){nums = (int*)malloc(matrixRowSize * sizeof(int));for (row = 0; row < matrixRowSize; row++){nums[row] = matrix[row][0];}row = binary_search(nums, matrixRowSize, target);if (row >= 0){return true;}else{row = -row - 1;if (row == 0){return false;}else{row--;}}}int col = binary_search(matrix[row], matrixColSize, target);return col >= 0;
}int main()
{int row = 3;int col = 4;int target = 3;int **mat = (int**)malloc(row * sizeof(int *));mat[0] = (int*)malloc(col * sizeof(int));mat[0][0] = 1;mat[0][1] = 3;mat[0][2] = 5;mat[0][3] = 7;mat[1] = (int*)malloc(col * sizeof(int));mat[1][0] = 10;mat[1][1] = 11;mat[1][2] = 16;mat[1][3] = 20;mat[2] = (int*)malloc(col * sizeof(int));mat[2][0] = 23;mat[2][1] = 30;mat[2][2] = 34;mat[2][3] = 50;printf("%s\n", searchMatrix(mat, row, col, target) ? "true" : "false");return 0;
}输出:
true
改为C++ 用vector方便,代码比较简洁,
#include <bits/stdc++.h>
using namespace std;int binary_search(vector<int> nums, int len, int target)
{int low = -1;int high = len;while (low + 1 < high) {int mid = low + (high - low) / 2;if (target > nums[mid])low = mid;elsehigh = mid;}if (high == len || nums[high] != target)return -high - 1;elsereturn high;
}bool searchMatrix(vector<vector<int>> matrix, int target)
{int matrixRowSize = matrix.size();int matrixColSize = matrix.front().size();if (matrixRowSize == 0 || matrixColSize == 0)return false;if (target < matrix.front().front() || target > matrix[matrixRowSize - 1][matrixColSize - 1])return false;int row = 0;vector<int> nums(matrixRowSize);if (matrixRowSize > 0) {for (row = 0; row < matrixRowSize; row++)nums[row] = matrix[row][0];row = binary_search(nums, matrixRowSize, target);if (row < 0) {row = -row - 1;if (row != 0) row--;else return false;} else return true;}int col = binary_search(matrix[row], matrixColSize, target);return col >= 0;
}int main()
{vector<vector<int>> matrix = {{1,3,5,7},{10,11,16,20},{23,30,34,60}};cout << (searchMatrix(matrix, 3) ? "true" : "false") << endl;cout << (searchMatrix(matrix, 13) ? "true" : "false") << endl;return 0;
}3. 三角形最小路径和
给定一个三角形 triangle ,找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。
示例 1:
输入:triangle = [[2],[3,4],[6,5,7],[4,1,8,3]] 输出:11 解释:如下面简图所示: 2 3 4 6 5 7 4 1 8 3 自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
示例 2:
输入:triangle = [[-10]] 输出:-10
提示:
1 <= triangle.length <= 200triangle[0].length == 1triangle[i].length == triangle[i - 1].length + 1-10^4 <= triangle[i][j] <= 10^4
进阶:
- 你可以只使用
O(n)的额外空间(n为三角形的总行数)来解决这个问题吗?
代码:
#include <bits/stdc++.h>
using namespace std;class Solution
{
public:int minimumTotal(vector<vector<int>> &triangle){int n = triangle.size();if (n == 0)return 0;if (n == 1)return triangle[0][0];vector<vector<int>> info(n, vector<int>(n, 0));info[0][0] = triangle[0][0];for (int i = 1; i < n; ++i){for (int j = 0; j <= i; ++j){if (j == 0)info[i][j] = triangle[i][j] + info[i - 1][j];else if (j == i)info[i][j] = triangle[i][j] + info[i - 1][j - 1];else{int temp = info[i - 1][j] > info[i - 1][j - 1] ? info[i - 1][j - 1] : info[i - 1][j];info[i][j] = temp + triangle[i][j];}}}int res = info[n - 1][0];for (int i = 0; i < n; ++i){if (info[n - 1][i] < res){res = info[n - 1][i];}}return res;}
};int main()
{Solution s;vector<vector<int>> triangle = {{2},{3,4},{6,5,7},{4,1,8,3}};cout << s.minimumTotal(triangle) << endl;triangle = {{-10}};cout << s.minimumTotal(triangle) << endl;return 0;
}输出:
11
-10
附录
二分查找
又称折半查找、二分搜索、折半搜索等,是一种在静态查找表中查找特定元素的算法。
所谓静态查找表,即只能对表内的元素做查找和读取操作,不允许插入或删除元素。
使用二分查找算法,必须保证查找表中存放的是有序序列(升序或者降序)。
存储无序序列的静态查找表,除非先对数据进行排序,否则不能使用二分查找算法。
🌟 每日一练刷题专栏 🌟
✨ 持续,努力奋斗做强刷题搬运工!
👍 点赞,你的认可是我坚持的动力!
🌟 收藏,你的青睐是我努力的方向!
✎ 评论,你的意见是我进步的财富!
 | Golang 每日一练 专栏 |
|
| C/C++ 每日一练 专栏 |
|
| Python 每日一练 专栏 |
|
| Java 每日一练 专栏 |
相关文章:

C/C++每日一练(20230314)
目录 1. 移动数组中的元素 2. 搜索二维矩阵 3. 三角形最小路径和 🌟 每日一练刷题专栏 🌟 Golang 每日一练 专栏 C/C 每日一练 专栏 Python 每日一练 专栏 Java 每日一练 专栏 1. 移动数组中的元素 将一维数组中的元素循环左移 k 个位置 输入…...

裸辞3个月,面试了25家公司,终于找到心仪的工作了
上半年裁员,下半年裸辞,有不少人高呼裸辞后躺平真的好快乐!但也有很多人,裸辞后的生活五味杂陈。 面试25次终于找到心仪工作 因为工作压力大、领导PUA等各种原因,今年2月下旬我从一家互联网小厂裸辞,没…...
【Linux学习】进程间通信——system V(共享内存 | 消息队列 | 信号量)
🐱作者:一只大喵咪1201 🐱专栏:《Linux学习》 🔥格言:你只管努力,剩下的交给时间! 进程间通信——共享内存 | 消息队列 | 信号量🏀共享内存⚽系统调用shmgetkey值⚽系统…...
解决 IDA 防F5转伪C笔记
某app砸壳后放到IDA,根据堆栈查到该位置如下; G调到,0x1b81bcc 看下: BR 调到后面 x8 x9地址,汇编指令; 找到x9的地址,然后减去基地址也就是首地址,得到便宜地址; hook x9: var moduleAddr = Module.findBaseAddress("XX"); var line = moduleAddr.add...

【面试题】你需要知道的webpack高频面试题
大厂面试题分享 面试题库前后端面试题库 (面试必备) 推荐:★★★★★地址:前端面试题库谈谈你对webpack的看法webpack是一个模块打包工具,可以使用它管理项目中的模块依赖,并编译输出模块所需的静态文件。它…...

【YOLOv8/YOLOv7/YOLOv5/YOLOv4/Faster-rcnn系列算法改进NO.60】损失函数改进为wiou
前言作为当前先进的深度学习目标检测算法YOLOv8,已经集合了大量的trick,但是还是有提高和改进的空间,针对具体应用场景下的检测难点,可以不同的改进方法。此后的系列文章,将重点对YOLOv8的如何改进进行详细的介绍&…...
attack解析(详细))
2023年中职网络安全竞赛——数字取证调查(新版)attack解析(详细)
数字取证调查 任务环境说明: 服务器场景:FTPServer20221010(关闭链接)服务器场景操作系统:未知FTP用户名:attack817密码:attack817分析attack.pcapng数据包文件,通过分析数据包attack.pcapng找出恶意用户第一次访问HTTP服务的数据包是第几号,将该号数作为Flag值提交;…...

Cadence Allegro 导出Net Single Pin and No Pin报告详解
⏪《上一篇》 🏡《上级目录》 ⏩《下一篇》 目录 1,概述2,Net Single Pin and No Pin作用3,Net Single Pin and No Pin示例4,Net Single Pin and No Pin导出方法4.1,方法14.2,方法2B站关注“硬小二”浏览更多演示视频...
蓝桥冲刺31天之317
在这个时代,我们总是在比较,觉得自己不够好 其实不必羡慕别人的闪光点 每个人都是属于自己的限量版 做你喜欢并且擅长的事,做到极致 自然会找到自己独一无二的价值 鸟不跟鱼比游泳,鱼不跟鸟比飞翔 你我各有所长 A:组队…...
站上风口,文心一言任重道远
目录正式发布时机选择逻辑推理AI绘画用户选择总结自从OpenAI公司的chatGPT发布以来,吸引了全球目光,同时也引起了我们的羡慕,希望有国产的聊天机器人,盼星星盼月亮,终于等来了百度文心一言的发布。 正式发布 3月16日…...

Qt音视频开发24-视频显示QOpenGLWidget方式(占用GPU)
一、前言 采用painter的方式绘制解码后的图片,方式简单易懂,巨大缺点就是占CPU,一个两个通道还好,基本上CPU很低,但是到了16个64个通道的时候,会发现CPU也是很吃紧(当然强劲的电脑配置另当别论…...

百度发布文心一言,我想说几句
大家好,我是记得诚。 今天下午百度公司正式发布了文心一言,算是国内第一个交卷的互联网公司。 在ChatGPT和GPT-4的双重夹击下,可想而知百度的压力。 ChatGPT发布的时候,热度非常的高,大家对其都非常的感兴趣。 我是…...

简单了解JSP
JSP概念与原理概念: Java Server Pages,Java服务端页面一种动态的网页技术,其中既可以定义 HTML、JS、CSS等静态内容,还可以定义Java代码的动态内容JSP HTML Java, 用于简化开发JSP的本质上就是一个ServletJSP 在被访问时,由JSP容…...
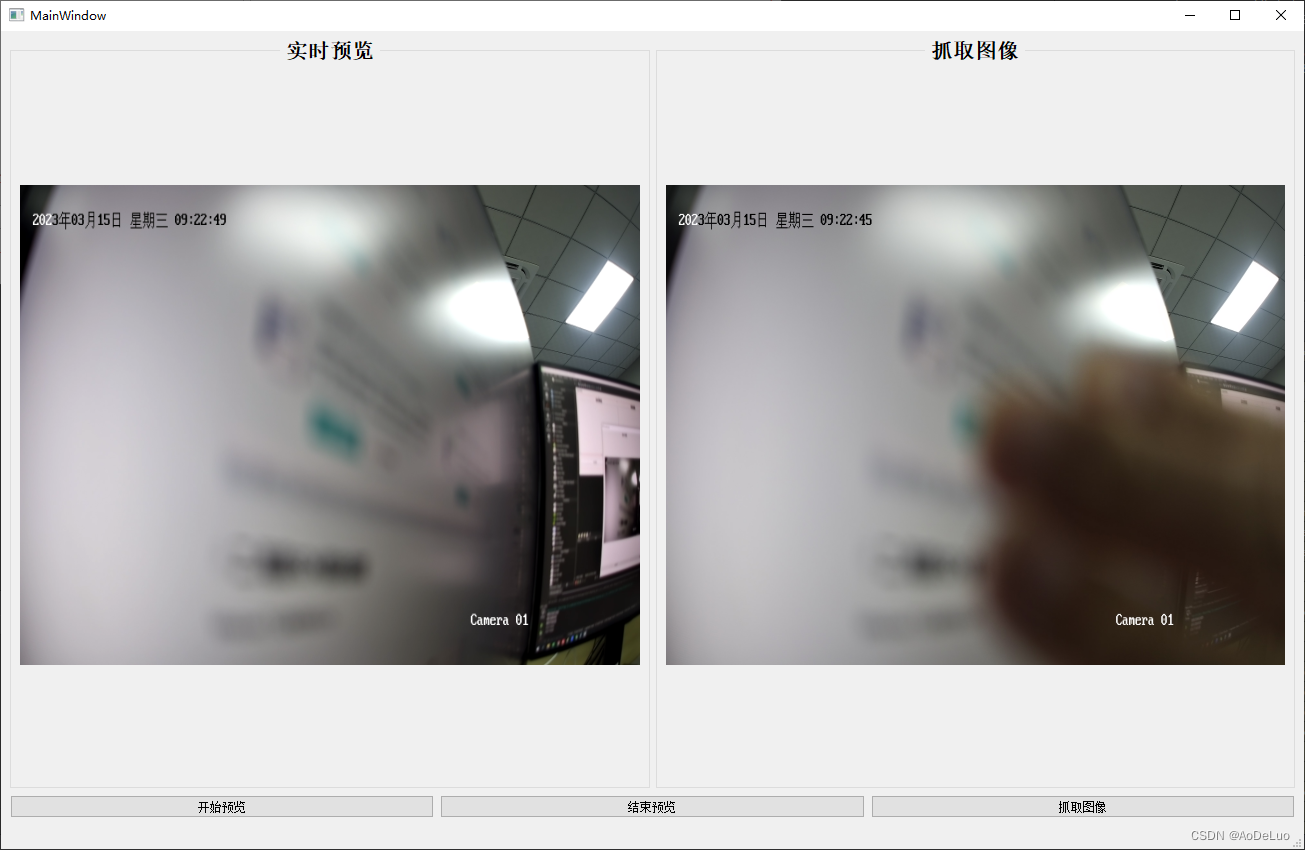
Qt(c++)调用海康威视监控摄像头
文章目录一.海康威视监控摄像头开发SDK介绍二.海康SDK模块说明三.Qt项目中海康威视SDK配置四.实时预览摄像头图像程序一.海康威视监控摄像头开发SDK介绍 设备网络SDK是基于设备私有网络通信协议开发的,为嵌入式网络硬盘录像机、NVR、网络摄像机、网络球机、视频服务…...
: CUDA_Run_Time_API_parallel_多流并行,以及多流之间互相同步等待的操作方式)
深度学习部署笔记(十五): CUDA_Run_Time_API_parallel_多流并行,以及多流之间互相同步等待的操作方式
// CUDA运行时头文件 #include <cuda_runtime.h>#include <chrono> #include <stdio.h> #include <string.h>using namespace std;#define checkRuntime(op) __check_cuda_runtime((op), #op, __FILE__, __LINE__)bool __check_cuda_runtime(cudaErro…...
【Spring】spring框架简介
一、框架 1.框架的基本特点: 框架(Framework),是基于基础技术之上,从众多业务中抽取出的通用解决方案;框架是一个半成品,使用框架规定的语法开发可以提高开发效率,可以用简单的代码就能完成复杂的基础业务;框架内部使用大量的设…...

WuThreat身份安全云-TVD每日漏洞情报-2023-03-17
漏洞名称:TP-LINK Archer AX21 命令注入漏洞 漏洞级别:严重 漏洞编号:CVE-2023-1389,CNNVD-202303-1280 相关涉及:TP-LINK Archer AX21 1.1.4 Build 20230219之前的固件版本 漏洞状态:POC 参考链接:https://tvd.wuthreat.com/#/listDetail?TVD_IDTVD-2023-06347 漏洞名称:D-L…...

postman 调用webservice
有个外部接口需要提供古老的webservice 格式接口。1 设置格式按照xml 格式设置。2 消息体xml 封装不加envelope:<soap:Envelope xmlns:soap"" target"_blank">http://schemas.xmlsoap.org/soap/envelope/"><soap:Body><soap:Fault&…...
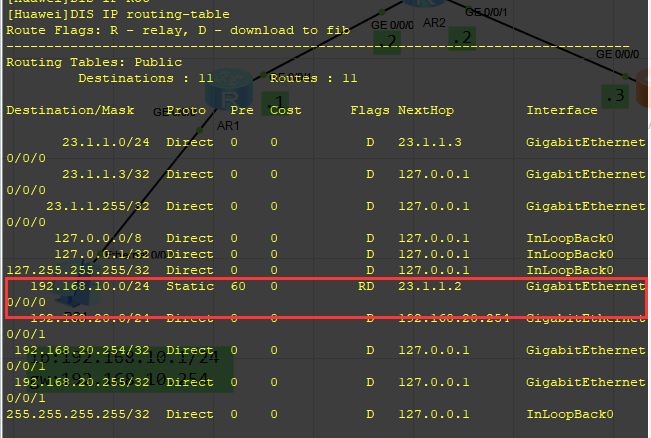
基于华为模拟器(ensp)的静态路由配置实验
一 实验需求静态路由实验,建立拓扑pc1>>R1>>R2>>R3>>pc2,使pc1与pc2能相互通信。二 实验拓扑三 ip地址规划设备接口ip地址AR1G0/0/0192.168.10.254/24G0/0/112.1.1.1/24AR2G0/0/012.1.1.2/24G0/0/123.1.1.2/24 AR3G0/0/023.1.1.…...
模拟实现字符串函数(长度受限制的详讲)
上次发布了长度不受限制的字符串函数的模拟实现方法,这次就给大家说说长度受限制的字符串函数。首先,长度受限制和不受限制有什么区别呢?其实从某种意义上来讲,长度受限制的字符串函数比长度不受限制的字符串安全,为什…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...


