3112. 访问消失节点的最少时间 Medium

给你一个二维数组 edges 表示一个 n 个点的无向图，其中 edges[i] = [ui, vi, lengthi] 表示节点 ui 和节点 vi 之间有一条需要 lengthi 单位时间通过的无向边。

同时给你一个数组 disappear ，其中 disappear[i] 表示节点 i 从图中消失的时间点，在那一刻及以后，你无法再访问这个节点。

注意，图有可能一开始是不连通的，两个节点之间也可能有多条边。

请你返回数组 answer ，answer[i] 表示从节点 0 到节点 i 需要的 最少 单位时间。如果从节点 0 出发 无法 到达节点 i ，那么 answer[i] 为 -1 。

示例 1：

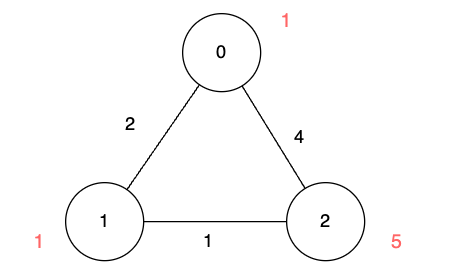
输入：n = 3, edges = [[0,1,2],[1,2,1],[0,2,4]], disappear = [1,1,5]

输出：[0,-1,4]

解释：

我们从节点 0 出发，目的是用最少的时间在其他节点消失之前到达它们。

 ·对于节点 0 ，我们不需要任何时间，因为它就是我们的起点。

 ·对于节点 1 ，我们需要至少 2 单位时间，通过 edges[0] 到达。但当我们到达的时候，它已经消失了，所以我们无法到达它。

 ·对于节点 2 ，我们需要至少 4 单位时间，通过 edges[2] 到达。

示例 2：

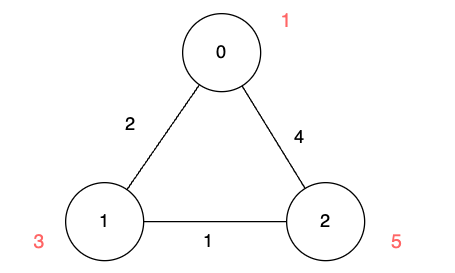
输入：n = 3, edges = [[0,1,2],[1,2,1],[0,2,4]], disappear = [1,3,5]

输出：[0,2,3]

解释：

我们从节点 0 出发，目的是用最少的时间在其他节点消失之前到达它们。

 ·对于节点 0 ，我们不需要任何时间，因为它就是我们的起点。

 ·对于节点 1 ，我们需要至少 2 单位时间，通过 edges[0] 到达。

 ·对于节点 2 ，我们需要至少 3 单位时间，通过 edges[0] 和 edges[1] 到达。

示例 3：

输入：n = 2, edges = [[0,1,1]], disappear = [1,1]

输出：[0,-1]

解释：

当我们到达节点 1 的时候，它恰好消失，所以我们无法到达节点 1 。

提示：

 ·1 <= n <= 5 * 104

 ·0 <= edges.length <= 105

 ·edges[i] == [ui, vi, lengthi]

 ·0 <= ui, vi <= n - 1

 ·1 <= lengthi <= 105

 ·disappear.length == n

 ·1 <= disappear[i] <= 105

题目大意：只有在各结点的规定时间内才能访问各结点的情况下计算从0到达各结点的最短时间。

分析：

（1）由题可知这是单源最短路径问题，因此使用dijkstra算法；

（2）由于题中结点个数较多，因此使用优先级队列存储已访问过的结点中可以直接到达的未访问过的结点来加速查找距离0结点最近且未访问过的点；

（3）对于在规定时间外访问的结点只需不将其加入优先级队列即可。

class Solution {
public:vector<int> minimumTime(int n, vector<vector<int>>& edges, vector<int>& disappear) {int x,y,t,node,time,nt;vector<int> ans(n,-1);priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> q;vector<vector<pair<int,int>>> map(n);for(const auto& edge:edges){x=edge[0];y=edge[1];t=edge[2];if(x==y) continue;map[x].emplace_back(y,t);map[y].emplace_back(x,t);}q.emplace(0,0);ans[0]=0;while(q.size()){auto [time,node]=q.top();q.pop();if(time!=ans[node]) continue;for(const auto& [nextNode,nextTime]:map[node]){if((nt=time+nextTime)<disappear[nextNode]&&(ans[nextNode]==-1)||nt<ans[nextNode]){ans[nextNode]=nt;q.emplace(nt,nextNode);}}}return ans;}
};