如何实现布隆过滤器?
1.布隆过滤器的场景
在Redis 缓存击穿(失效)、缓存穿透、缓存雪崩怎么解决?中我们说到可以使用布隆过滤器避免「缓存穿透」。
你会说我们只要记录了每个用户看过的历史记录,每次推荐的时候去查询数据库过滤存在的数据实现去重。
实际上,如果历史记录存储在关系数据库里,去重就需要频繁地对数据库进行 exists 查询,当系统并发量很高时,数据库是很难扛住压力的。
我们不能使用缓存 将历史数据存在Redis中,这么多的历史记录那要浪费多大的内存空间,所以这个时候我们就能使用布隆过滤器去解决这种去重问题。又快又省内存,互联网开发必备杀招!
当我们遇到数据量比较大,又需要去重的时候就可以考虑布隆过滤器,如下场景:
- 解决 Redis 缓存穿透问题(面试重点);
- 利用布隆过滤器我们可以预先把数据查询的主键,比如用户 ID 或文章 ID 缓存到过滤器中。当根据 ID 进行数据查询的时候,我们先判断该 ID 是否存在,若存在的话,则进行下一步处理。若不存在的话,直接返回,这样就不会触发后续的数据库查询。需要注意的是缓存穿透不能完全解决,我们只能将其控制在一个可以容忍的范围内。
- 邮件过滤,使用布隆过滤器实现邮件黑名单过滤;
- 反垃圾邮件,从数十亿个垃圾邮件列表中判断某邮箱是否垃圾邮箱;
- 网页爬虫对 URL 去重,避免爬取相同的 URL 地址;
- Google Chrome 使用布隆过滤器识别恶意 URL;
- Medium 使用布隆过滤器避免推荐给用户已经读过的文章;
- 推荐过的新闻不再推荐;
- Google BigTable,Apache HBbase 和 Apache Cassandra 使用布隆过滤器减少对不存在的行和列的查找。
2.布隆过滤器的概述
布隆过滤器 (Bloom Filter)是由 Burton Howard Bloom 于 1970 年提出,它是一种 space efficient 的概率型数据结构,用于判断一个元素是否在集合中。
当布隆过滤器说,某个数据存在时,这个数据可能不存在;当布隆过滤器说,某个数据不存在时,那么这个数据一定不存在。
哈希表也能用于判断元素是否在集合中,但是布隆过滤器只需要哈希表的 1/8 或 1/4 的空间复杂度就能完成同样的问题。
布隆过滤器可以插入元素,但不可以删除已有元素。
其中的元素越多,false positive rate(误报率)越大,但是 false negative (漏报)是不可能的。
3.布隆过滤器原理
BloomFilter 的算法是,首先分配一块内存空间做 bit 数组,数组的 bit 位初始值全部设为 0。加入元素时,采用 k 个相互独立的 Hash 函数计算,然后将元素 Hash 映射的 K 个位置全部设置为 1。检测 key 是否存在,仍然用这 k 个 Hash 函数计算出 k 个位置,如果位置全部为 1,则表明 key 存在,否则不存在。
如下图所示:
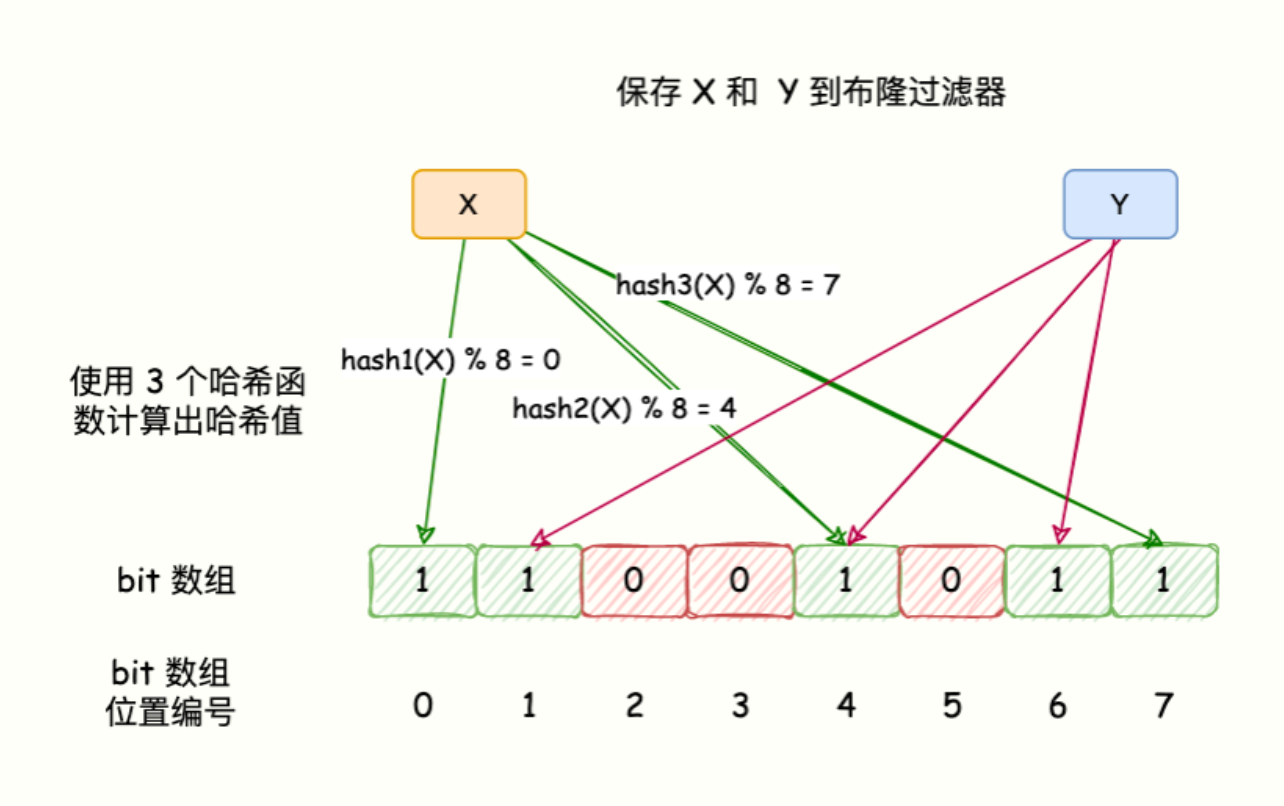
布隆过滤器原理
哈希函数会出现碰撞,所以布隆过滤器会存在误判。
这里的误判率是指,BloomFilter 判断某个 key 存在,但它实际不存在的概率,因为它存的是 key 的 Hash 值,而非 key 的值。
所以有概率存在这样的 key,它们内容不同,但多次 Hash 后的 Hash 值都相同。
对于 BloomFilter 判断不存在的 key ,则是 100% 不存在的,反证法,如果这个 key 存在,那它每次 Hash 后对应的 Hash 值位置肯定是 1,而不会是 0。布隆过滤器判断存在不一定真的存在。
布隆过滤器(Bloom Filter)本质上是由长度为 m 的位向量或位列表(仅包含 0 或 1 位值的列表)组成,最初所有的值均设置为 0,如下图所示。

为了将数据项添加到布隆过滤器中,我们会提供 K 个不同的哈希函数,并将结果位置上对应位的值置为 “1”。在前面所提到的哈希表中,我们使用的是单个哈希函数,因此只能输出单个索引值。而对于布隆过滤器来说,我们将使用多个哈希函数,这将会产生多个索引值。
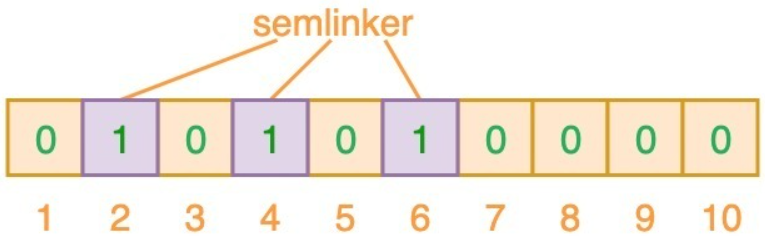
如上图所示,当输入 “semlinker” 时,预设的 3 个哈希函数将输出 2、4、6,我们把相应位置 1。假设另一个输入 ”kakuqo“,哈希函数输出 3、4 和 7。你可能已经注意到,索引位 4 已经被先前的 “semlinker” 标记了。此时,我们已经使用 “semlinker” 和 ”kakuqo“ 两个输入值,填充了位向量。当前位向量的标记状态为:
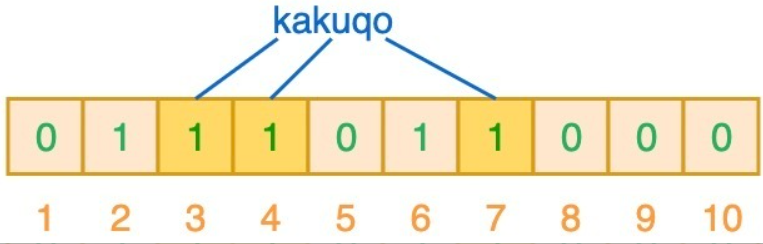
当对值进行搜索时,与哈希表类似,我们将使用 3 个哈希函数对 ”搜索的值“ 进行哈希运算,并查看其生成的索引值。假设,当我们搜索 ”fullstack“ 时,3 个哈希函数输出的 3 个索引值分别是 2、3 和 7:
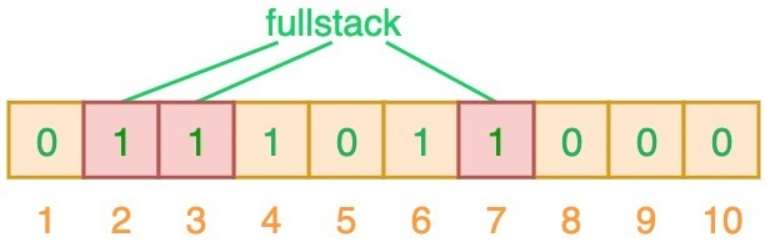
从上图可以看出,相应的索引位都被置为 1,这意味着我们可以说 ”fullstack“ 可能已经插入到集合中。事实上这是误报的情形,产生的原因是由于哈希碰撞导致的巧合而将不同的元素存储在相同的比特位上。幸运的是,布隆过滤器有一个可预测的误判率(FPP):
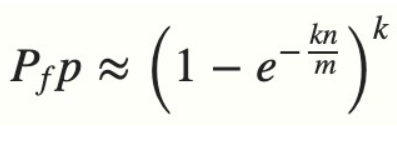
- n 是已经添加元素的数量(总的元素数量)
- k 哈希的次数
- m 布隆过滤器的长度(如比特数组的大小)
极端情况下,当布隆过滤器没有空闲空间时(满),每一次查询都会返回 true 。这也就意味着 m 的选择取决于期望预计添加元素的数量 n ,并且 m 需要远远大于 n 。
实际情况中,布隆过滤器的长度 m 可以根据给定的误判率(FPP)的和期望添加的元素个数 n 的通过如下公式计算:
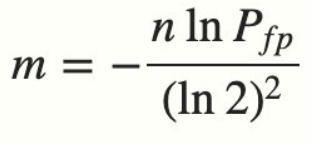
FPP越小说明了m的值越大 来实现m远大于n实现比特数组的长度更长。
了解完上述的内容之后,我们可以得出一个结论,当我们搜索一个值的时候,若该值经过 K 个哈希函数运算后的任何一个索引位为 ”0“,那么该值肯定不在集合中。但如果所有哈希索引值均为 ”1“,则只能说该搜索的值可能存在集合中。
为什么不允许删除元素?
删除意味着需要将对应的 k 个 bits 位置设置为 0,其中有可能是其他元素对应的位。
因此 remove 会引入 false negative,这是绝对不被允许的。
4.布隆过滤器优缺点
4.1.布隆过滤器优点
- 增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数,一般比较小),与数据量大小无关
- 哈希函数相互之间没有关系,方便硬件并行运算
- 布隆过滤器不需要存储元素本身,在某些对保密要求比较严格的场合有很大优势
- 在能够承受一定的误判时,布隆过滤器比其他数据结构有这很大的空间优势
- 数据量很大时,布隆过滤器可以表示全集,其他数据结构不能
- 使用同一组散列函数的布隆过滤器可以进行交、并、差运算
- 空间效率和查询时间都比一般的算法要好的多
4.2.布隆过滤器缺点
- 有误判率,即存在假阳性(False Position),即不能准确判断元素是否在集合中(补救方法:再建立一个白名单,存储可能会误判的数据)
- 不能获取元素本身
- 一般情况下不能从布隆过滤器中删除元素
- 如果采用计数方式删除,可能会存在计数回绕问题
- 存在一定的误识别率和删除困难
5.布隆过滤器的应用
布隆过滤器有很多实现和优化,由 Google 开发著名的 Guava 库就提供了布隆过滤器(Bloom Filter)的实现。在基于 Maven 的 Java 项目中要使用 Guava 提供的布隆过滤器,只需要引入以下环境:
<dependency><groupId>com.google.guava</groupId><artifactId>guava</artifactId><version>30.0-jre</version>
</dependency>
在导入 Guava 库后,我们新建一个 BloomFilterDemo 类,在 main 方法中我们通过 BloomFilter.create 方法来创建一个布隆过滤器,接着我们初始化 1 百万条数据到过滤器中,然后在原有的基础上增加 10000 条数据并判断这些数据是否存在布隆过滤器中:
package cn.wen;import com.google.common.base.Charsets;
import com.google.common.hash.BloomFilter;
import com.google.common.hash.Funnels;/*** 布隆过滤器测试*/
public class BloomFilterDemo {public static void main(String[] args) {int total = 1000000; // 总数量BloomFilter<CharSequence> bf =BloomFilter.create(Funnels.stringFunnel(Charsets.UTF_8), total,0.0002);// 初始化 1000000 条数据到过滤器中for (int i = 0; i < total; i++) {bf.put("" + i);}// 判断值是否存在过滤器中int count = 0;for (int i = 0; i < total + 10000; i++) {if (bf.mightContain("" + i)) {count++;}}System.out.println("已匹配数量 " + count);}}当以上代码运行后,控制台会输出以下结果:
已匹配数量 1000309
很明显以上的输出结果已经出现了误报,因为相比预期的结果多了 309 个元素,误判率为:
309/(1000000 + 10000) * 100 ≈ 0.030594059405940593
如果要提高匹配精度的话,我们可以在创建布隆过滤器的时候设置误判率 fpp:
BloomFilter<CharSequence> bf = BloomFilter.create(Funnels.stringFunnel(Charsets.UTF_8), total, 0.0002);
在 BloomFilter 内部,误判率 fpp 的默认值是 0.03:
// com/google/common/hash/BloomFilter.class
public static <T> BloomFilter<T> create(Funnel<? super T> funnel, long expectedInsertions) {return create(funnel, expectedInsertions, 0.03D);
}
在重新设置误判率为 0.0002 之后,我们重新运行程序,这时控制台会输出以下结果:
已匹配数量 1000003
通过观察以上的结果,可知误判率 fpp 的值越小,匹配的精度越高。当减少误判率 fpp 的值,需要的存储空间也越大,所以在实际使用过程中需要在误判率和存储空间之间做个权衡。
方案1:开发定时任务,每隔几个小时,自动创建一个新的布隆过滤器数组,替换老的,有点CopyOnWriteArrayList的味道
方案2:布隆过滤器增加一个等长的数组,存储计数器,主要解决冲突问题,每次删除时对应的计数器减一,如果结果为0,更新主数组的二进制值为0
6、手写布隆过滤器
/**
* @ClassName: BloomFilter
* @Author: 小飞
* @Date: 2023/5/17 21:50
* @Description: 布隆过滤器
*/
public class BloomFilter {// 默认大小private static final int DEFAULT_SIZE = Integer.MAX_VALUE;// 最小的大小private static final int MIN_SIZE = 1000;// 大小为默认大小private int SIZE = DEFAULT_SIZE;// hash函数的种子因子private static final int[] HASH_SEEDS = new int[]{3, 5, 7, 11, 13, 17, 19, 23, 29, 31};// 位数组,0/1,表示特征private BitSet bitSet = null;// hash函数private HashFunction[] hashFunctions = new HashFunction[HASH_SEEDS.length];// 无参数初始化public BloomFilter() {// 按照默认大小init();}// 带参数初始化public BloomFilter(int size) {// 大小初始化小于最小的大小if (size >= MIN_SIZE) {SIZE = size;}init();}// 初始化private void init() {// 初始化位大小bitSet = new BitSet(SIZE);// 初始化hash函数for (int i = 0; i < HASH_SEEDS.length; i++) {hashFunctions[i] = new HashFunction(SIZE, HASH_SEEDS[i]);}}// 添加元素,相当于把元素的特征添加到位数组中public void add(Object value) {for (HashFunction f : hashFunctions) {// 将hash值计算出来的值为truebitSet.set(f.hash(value), true);}}// 判断元素的特征是否存在于位数组public boolean contains(Object value) {boolean result = true;for (HashFunction f : hashFunctions) {result = result && bitSet.get(f.hash(value));// hash函数只要有一个计算出为false,则直接返回if (!result) {return false;}}return true;}// hash函数public static class HashFunction {// 位数组大小private int size;// hash种子private int seed;public HashFunction(int size, int seed) {this.size = size;this.seed = seed;}// hash函数public int hash(Object value) {if (value == null) {return 0;} else {// hash值int hash1 = value.hashCode();// 高位的hash值int hash2 = hash1 >>> 16;// 合并hash值 结合高低位特征int combineHash = hash1 ^ hash2;// 相乘取余return Math.abs(combineHash * seed) % size;}}}public static void main(String[] args) {Integer num1 = new Integer(12321);Integer num2 = new Integer(12345);BloomFilter myBloomFilter =new BloomFilter();System.out.println(myBloomFilter.contains(num1));System.out.println(myBloomFilter.contains(num2));myBloomFilter.add(num1);myBloomFilter.add(num2);System.out.println(myBloomFilter.contains(num1));System.out.println(myBloomFilter.contains(num2));}
}上面未提供Hash函数的数量,默认值实现hash函数。
// 带参数初始化
public BloomFilter(int num,double rate) {// 计算位数组的大小this.SIZE = (int) (-num * Math.log(rate) / Math.pow(Math.log(2), 2));// hash 函数个数this.s = (int) (this.SIZE * Math.log(2) / num);// 初始化位数组this.bitSet = new BitSet(SIZE);
}
上面的构造函数就是对误差率的初始化值。
相关文章:
如何实现布隆过滤器?
1.布隆过滤器的场景 在Redis 缓存击穿(失效)、缓存穿透、缓存雪崩怎么解决?中我们说到可以使用布隆过滤器避免「缓存穿透」。 你会说我们只要记录了每个用户看过的历史记录,每次推荐的时候去查询数据库过滤存在的数据实现去重。 …...

运维团队如何高效监控容器化环境中的PID及其他关键指标
随着云计算和容器化技术的快速发展,越来越多的企业开始采用容器化技术来部署和管理应用程序。然而,容器化环境的复杂性和动态性给运维团队带来了前所未有的挑战。本文将从PID(进程标识符)监控入手,探讨运维团队如何高效…...

通过vue3 + TypeScript + uniapp + uni-ui 实现下拉刷新和加载更多的功能
效果图: 核心代码: <script lang="ts" setup>import { ref, reactive } from vue;import api from @/request/api.jsimport empty from @/component/empty.vueimport { onLoad,onShow, onPullDownRefresh, onReachBottom } from @dcloudio/uni-applet form …...

Pointnet++改进即插即用系列:全网首发WTConv2d大接受域的小波卷积|即插即用,提升特征提取模块性能
简介:1.该教程提供大量的首发改进的方式,降低上手难度,多种结构改进,助力寻找创新点!2.本篇文章对Pointnet++特征提取模块进行改进,加入WTConv2d,提升性能。3.专栏持续更新,紧随最新的研究内容。 目录 1.理论介绍 2.修改步骤 2.1 步骤一 2.2 步骤二 2.3 步骤三 1.理…...
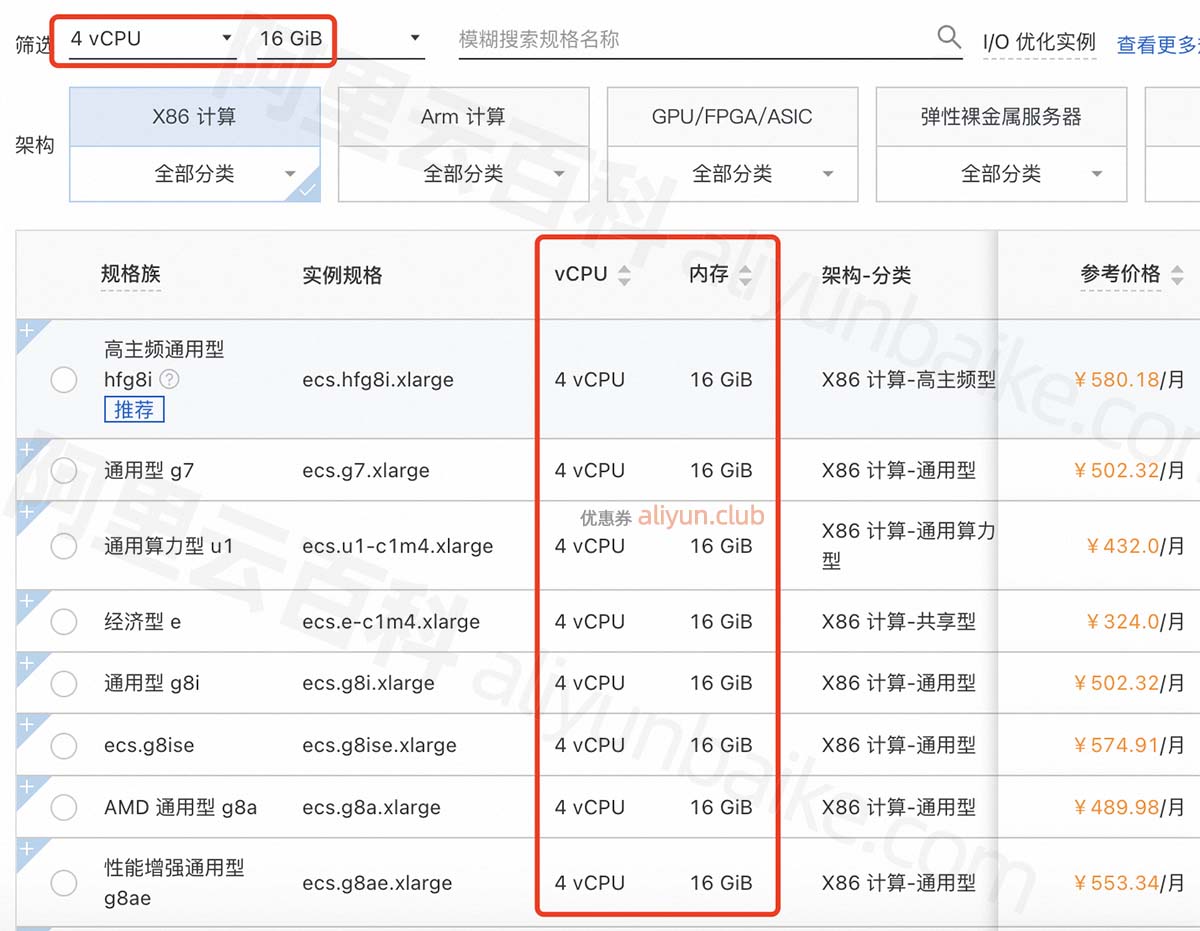
4核16G服务器支持多少人?4C16G服务器性能测评
租赁4核16G服务器费用,目前4核16G服务器10M带宽配置70元1个月、210元3个月,那么能如何呢?配置为ECS经济型e实例4核16G、按固定带宽10Mbs、100GB ESSD Entry系统盘。 那么问题来了,4C16G10M带宽的云服务器可以支持多少人同时在线&…...

塔子哥的平均数-美团2023笔试(codefun2000)
题目链接 塔子哥的平均数-美团2023笔试(codefun2000) 题目内容 给定一个正整数数组a1 ,a2 ,…,an,求平均数正好等于k的最长连续子数组的长度 输入描述 输出描述 输出一个整数,表示最长满足题目条件的长度。 样例1 输入 5 2 1 3 2 4 1 输出 3 样例1解释…...

故障诊断 | 基于小波包能量谱对滚动轴承的故障诊断Matlab代码
故障诊断 | 基于小波包能量谱对滚动轴承的故障诊断Matlab代码 目录 故障诊断 | 基于小波包能量谱对滚动轴承的故障诊断Matlab代码效果一览基本介绍程序设计参考资料 效果一览 基本介绍 基于小波包能量谱对滚动轴承的故障诊断 matlab代码 数据采用的是凯斯西储大学数据 首先利用…...

E14.【C语言】练习:有关短路运算
#include <stdio.h> int main() {int i 0,a0,b2,c 3,d4;i a && b && d;printf("a %d\nb %d\nc %d\nd %d\n", a, b, c, d);return 0; } 求输出结果 分析: a:先使用后 ,a(见第15篇http://…...

python BeautifulSoup库安装与使用(anaconda、pip)
BeautifulSoup 是一个可以从HTML或XML文件中提取数据的Python库。Beautiful Soup 已成为和 lxml、html5lib 一样出色的Python解释器,为用户灵活地提供不同的解析策略或强劲的速度。 Requests 获取html BeautifulSoup 解析html、xml,BeautifulSoup4库也称bs4库 安装B…...

基于Matlab的数据可视化
基于Matlab的数据可视化 一、二维图形的绘制(一)基本图形函数(1)plot函数(2)fplot函数(3)其他坐标系的二维曲线 (二)图形属性设置(1)线…...

深入理解Linux网络(二):UDP接收内核探究
深入理解Linux网络(二):UDP接收内核探究 一、UDP 协议处理二、recvfrom 系统调⽤实现 一、UDP 协议处理 udp 协议的处理函数是 udp_rcv。 //file: net/ipv4/udp.c int udp_rcv(struct sk_buff *skb) {return __udp4_lib_rcv(skb, &udp_…...

linux内核中list的基本用法
内核链表 1 list_head 结构 为了使用链表机制,驱动程序需要包含<linux/types.h>头文件,该文件定义了如下结构体实现双向链: struct list_head {struct list_head *next, *prev; };2 链表的初始化 2.1 链表宏定义和初始化 可使用以…...

项目中无关痛痒的词句背后深层含义
项目中听上去无关痛痒的词句背后,深层含义有的时候并不友善。 他们说的:进度表有些激进 真正的意思:我们有麻烦了 他们说的:我们将在接下来的几个迭代里面弥补延误 真正的意思:我们还是有麻烦 他们说的࿱…...
身份验证)
DLMS协议中的高级安全(HLS)身份验证
1.四步身份验证协议 在IEC 62056-53中已说明,ACSE提供部分高级身份安全(HLS)验证服务。高级身份安全验证适用于通信通道不能提供内部安全,应采取防范措施以防止偷听和信息(密码)重现的情况。这时ÿ…...
)
2024“钉耙编程”杭电多校1006 序列立方(思维+前缀和优化dp)
来源 题目 Problem Description 给定长度为 N 的序列 a。 一个序列有很多个子序列,每个子序列在序列中出现了若干次。 小马想请你输出序列 a 每个非空子序列出现次数的立方值的和,答案对 998244353 取模。 你可以通过样例解释来辅助理解题意。 Input 第…...
钡铼分布式I/O系统边缘计算Modbus,MQTT,OPC UA耦合器BL206
BL206系列耦合器是一个数据采集和控制系统,基于强大的32 位微处理器设计,采用Linux操作系统,支持Modbus,MQTT,OPC UA协议,可以快速接入现场PLC、DCS、PAS、MES、Ignition和SCADA以及ERP系统,同时…...

防火墙--双机热备
目录 双击热备作用 防火墙和路由器备份不同之处 如何连线 双机 热备 冷备 VRRP VGMP(华为私有协议) 场景解释 VGMP作用过程 主备的形成场景 接口故障的切换场景 整机故障 原主设备故障恢复的场景 如果没有开启抢占 如果开启了抢占 负载分…...

机器学习 -逻辑回归的似然函数
公式解释 公式如下: L ( θ ) ∏ i 1 m P ( y i ∣ x i ; θ ) ∏ i 1 m ( h θ ( x i ) ) y i ( 1 − h θ ( x i ) ) 1 − y i L(\theta) \prod_{i1}^m P(y_i | x_i; \theta) \prod_{i1}^m (h_\theta(x_i))^{y_i} (1 - h_\theta(x_i))^{1 - y_i} L(θ)i1∏…...

go 实现websocket以及详细设计流程过程,确保通俗易懂
websocket简介: WebSocket 是一种网络传输协议,可在单个 TCP 连接上进行全双工通信,位于 OSI 模型的应用层。WebSocket 协议在 2011 年由 IETF 标准化为 RFC 6455,后由 RFC 7936 补充规范。 WebSocket 使得客户端和服务器之间的数…...

记录工作中遇到的关于更新丢失商品超开的一个坑
场景: 工作中使用MybatisPlus以及Oracle进行数据库操作,收到RocketMQ消息开始并发分摊不同清货单的商品的批次,并对商品更新冻结数量。 上线后频繁出现商品超库存开票问题。(还好是内部业务,人工替换批次记账即可&…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...

第21节 Node.js 多进程
Node.js本身是以单线程的模式运行的,但它使用的是事件驱动来处理并发,这样有助于我们在多核 cpu 的系统上创建多个子进程,从而提高性能。 每个子进程总是带有三个流对象:child.stdin, child.stdout和child.stderr。他们可能会共享…...
