技术掉：PDF显示，使用pdf.js
PDF 显示
场景： 其实直接显示 pdf 可以用 iframe 标签，但产品觉得浏览器自带的 pdf 预览太丑了，而且无法去除那些操作栏。
解决方案：使用 pdf.js 进行显示
第一步：引入 pdf.js
去官网下载稳定版的 pdf.js 文件
然后将下载好的文件放进项目的静态文件夹，我用的是 vite 项目，所以是 public
第二步：在页面中引入 viewer.html
<iframeclass="iframe1":src="'/public/pdf/web/viewer.html?file=xxxxxxx'"frameborder="0"width="100%"height="100%"
></iframe>
filte 是你的 pdf 的路径，本地路径和 url 路径都是可以的
设置好之后就可以预览了
效果如下：
遇到的问题
pdf 跨域
首先此插件跨域的话会报错，需要注释掉部分代码
/pdf/web/viewer.js
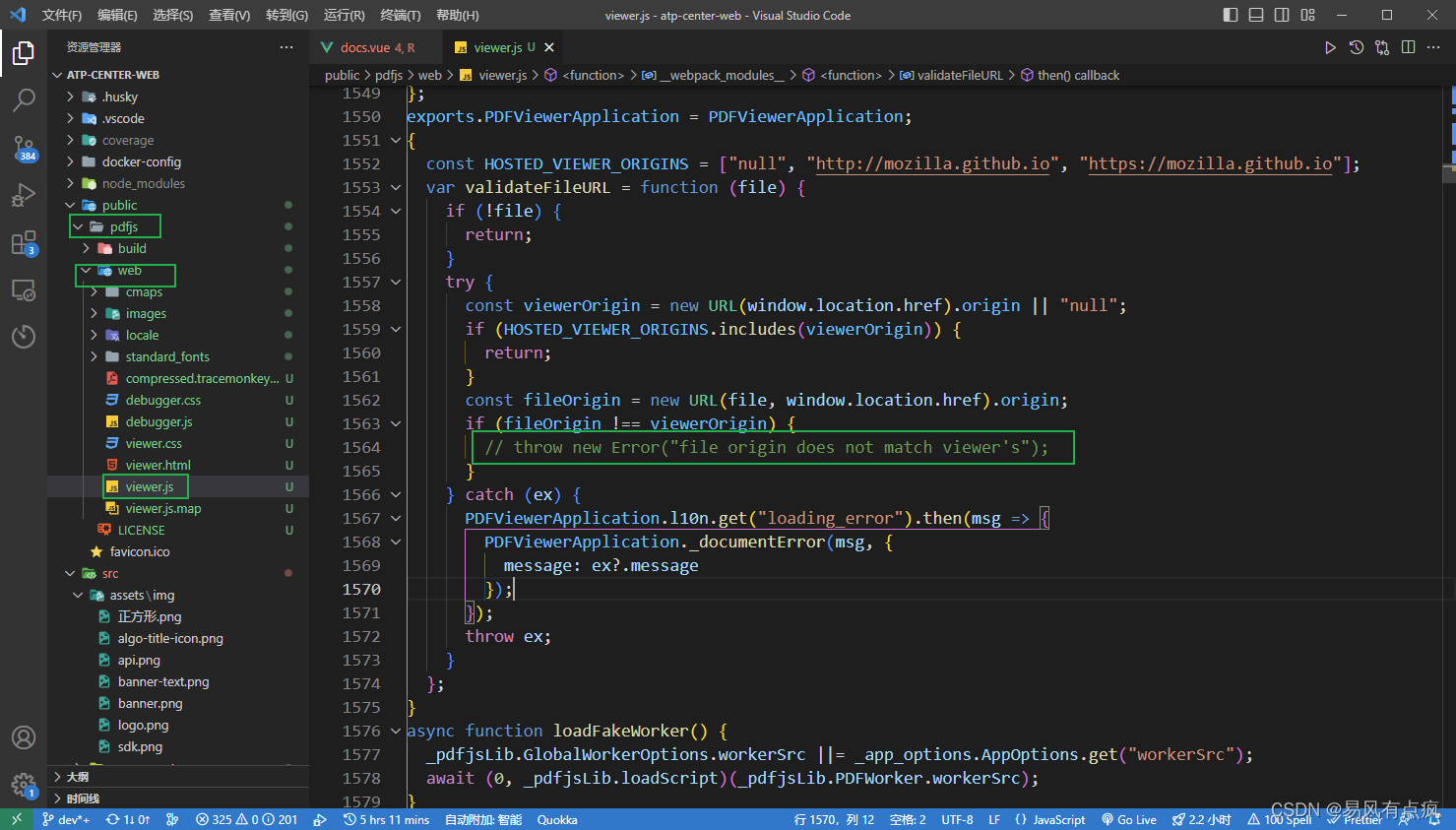
注释掉之后就可以解决了
更改 pdf 样式
直接去修改 viewer.html 里面的代码就行了
相关文章：
技术掉：PDF显示，使用pdf.js
PDF 显示 场景： 其实直接显示 pdf 可以用 iframe 标签，但产品觉得浏览器自带的 pdf 预览太丑了，而且无法去除那些操作栏。 解决方案：使用 pdf.js 进行显示 第一步：引入 pdf.js 去官网下载稳定版的 pdf.js 文件 然后…...
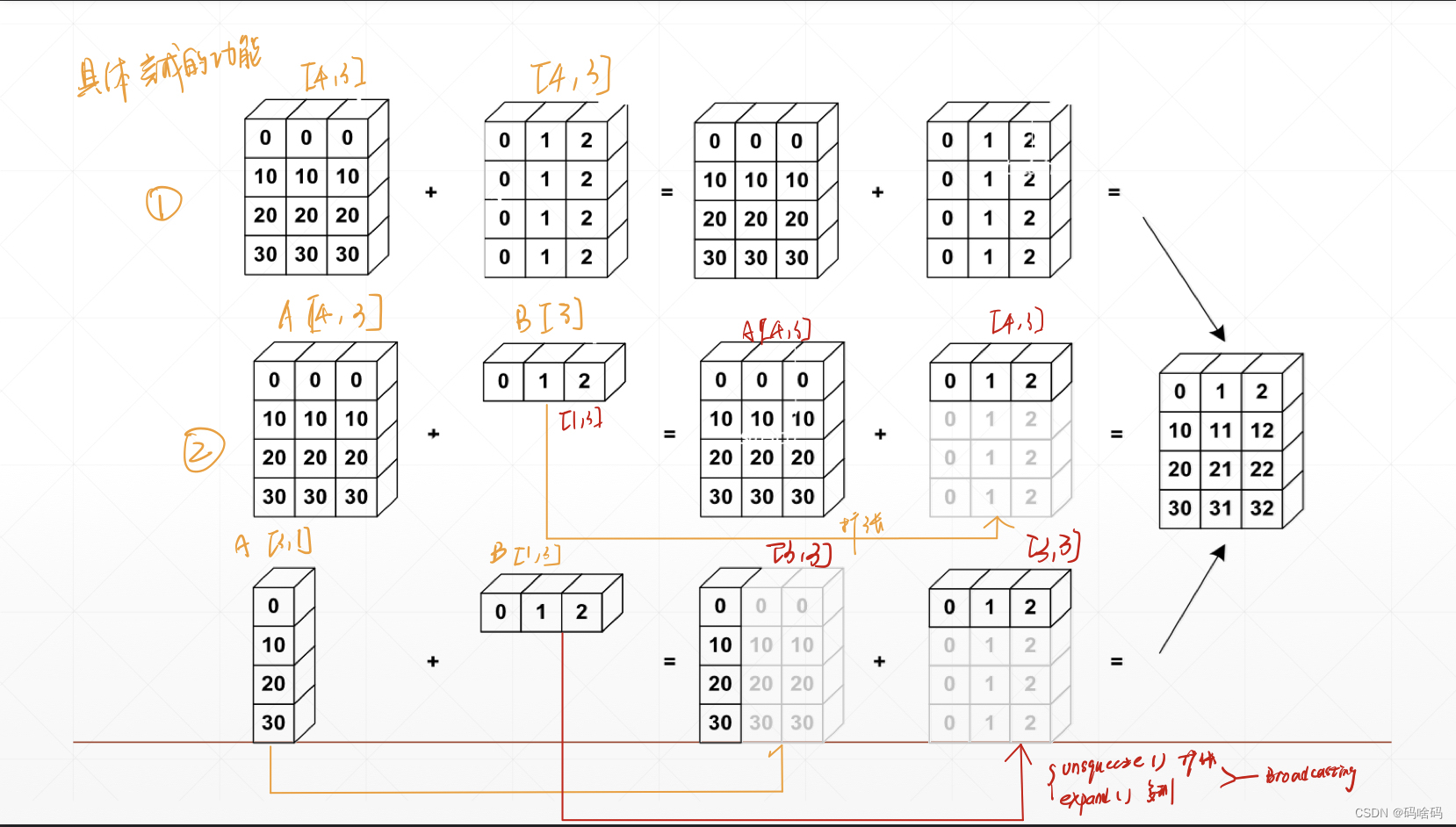
有关pytorch的一些总结
Tensor 含义 张量（Tensor）：是一个多维数组，它是标量、向量、矩阵的高维拓展。 创建 非随机创建 1.用数组创建 将数组转化为tensor np.ones([a,b]) 全为1 #首先导入PyTorch import torch#数组创建 import numpy as np anp.arr…...
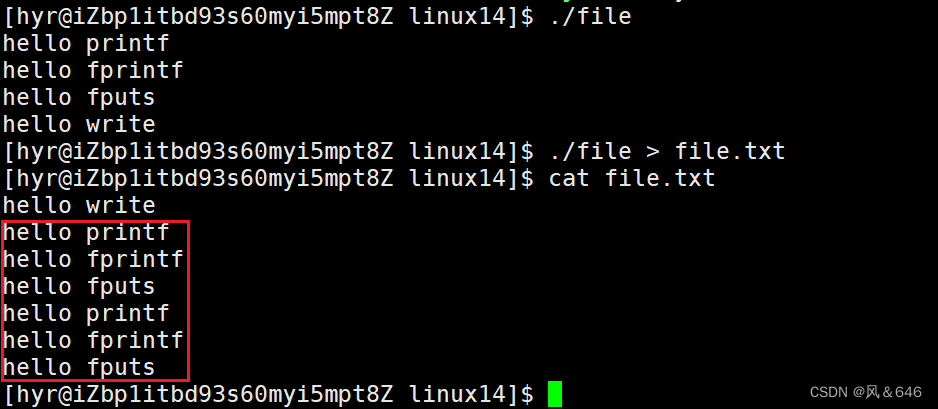
基础IO【Linux】
文章目录：文件相关知识C语言文件IOstdin & stdout & stderr系统文件 IOopenclosewriteread文件描述符文件描述符的分配规则重定向dup2系统调用FILEFILE中的文件描述符FILE中的缓冲区理解文件相关知识 文件 文件内容 文件属性（每一个已经存在的…...
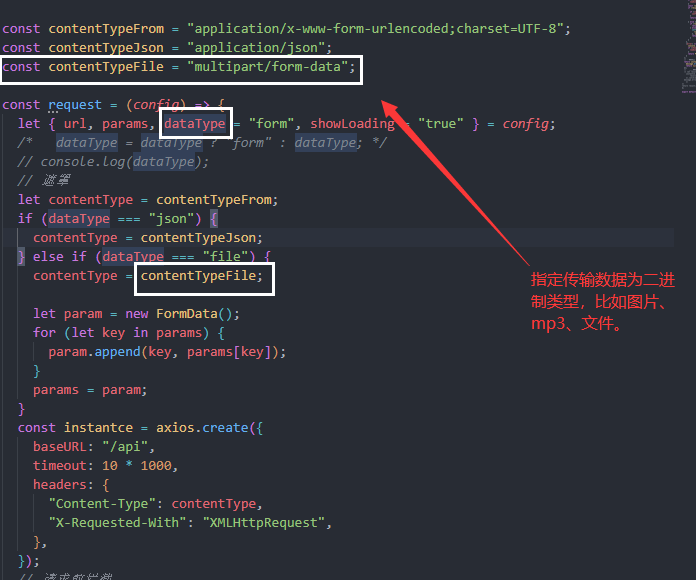
Vue3——自定义封装上传图片样式
自定义封装上传图片样式 一、首先需要新建一个自组建完善基础的结构，我这里起名为ImgUpload.vue <el-upload name"file" :show-file-list"false" accept".png,.PNG,.jpg,.JPG,.jpeg,.JPEG,.gif,.GIF,.bmp,.BMP" :multiple"…...
ChatGLM-6B (介绍以及本地部署)
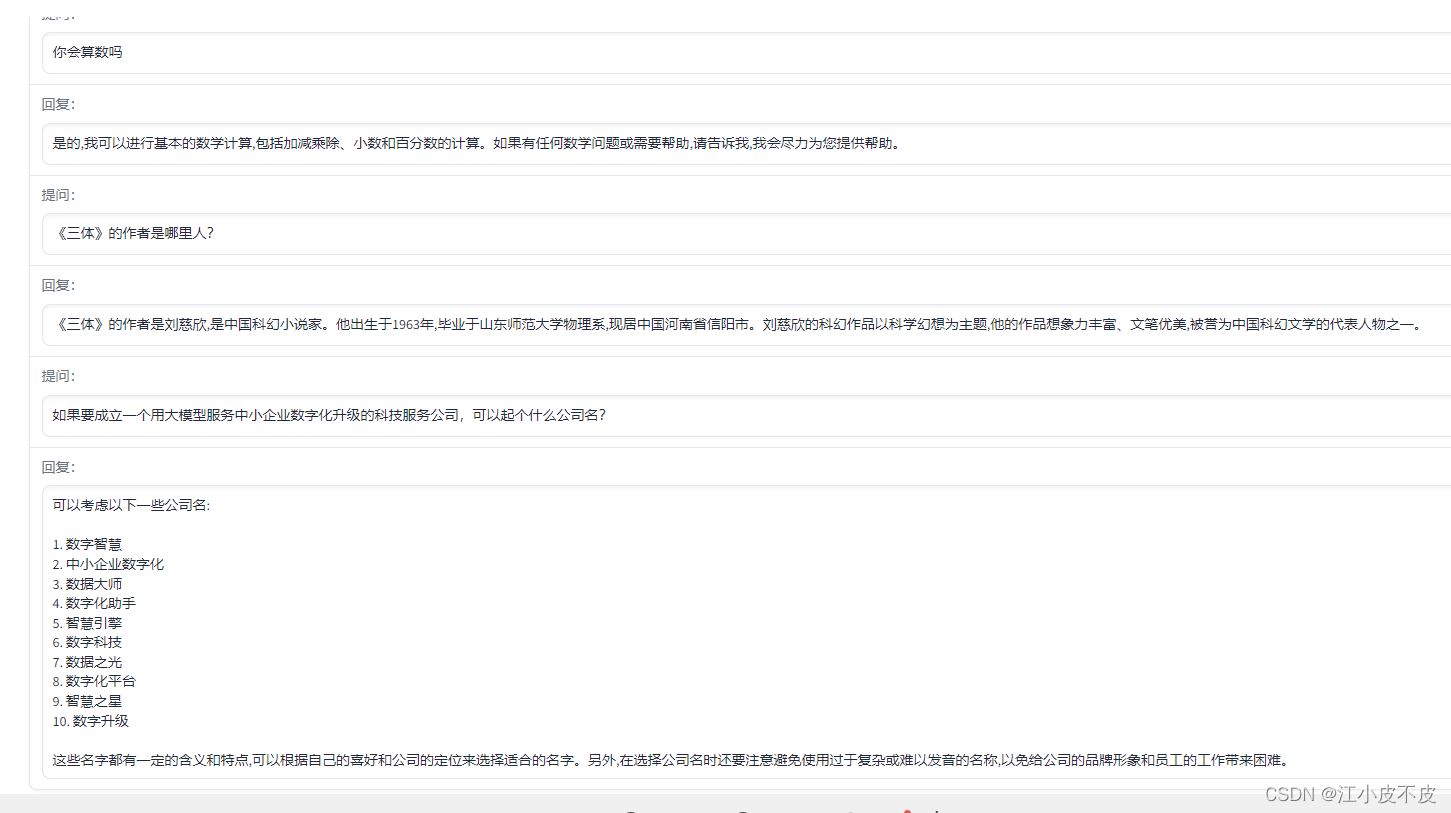
中文ChatGPT平替——ChatGLM-6BChatGLM-6B简介官方实例本地部署1.下载代码2.通过conda创建虚拟环境3.修改代码4.模型量化5.详细代码调用示例ChatGLM-6B 简介 ChatGLM-6B 是一个开源的、支持中英双语问答的对话语言模型，基于 General Language Model (GLM) 架构&…...
react的基础使用
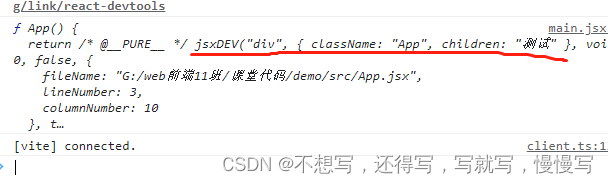
react中为什么使用jsxReact 认为渲染逻辑本质上与其他 UI 逻辑内在耦合，比如，在 UI 中需要绑定处理事件、在某些时刻状态发生变化时需要通知到 UI，以及需要在 UI 中展示准备好的数据。react认为将业务代码和数据以及事件等等 需要和UI高度耦合…...
letcode 4.寻找两个正序数组的中位数（官方题解笔记）
题目描述 给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。 算法的时间复杂度应该为 O(log (mn)) 。 1.二分查找 1.1思路 时间复杂度：O(log(mn)) 空间复杂度：O(1) 给定…...
【面试题系列】K8S常见面试题
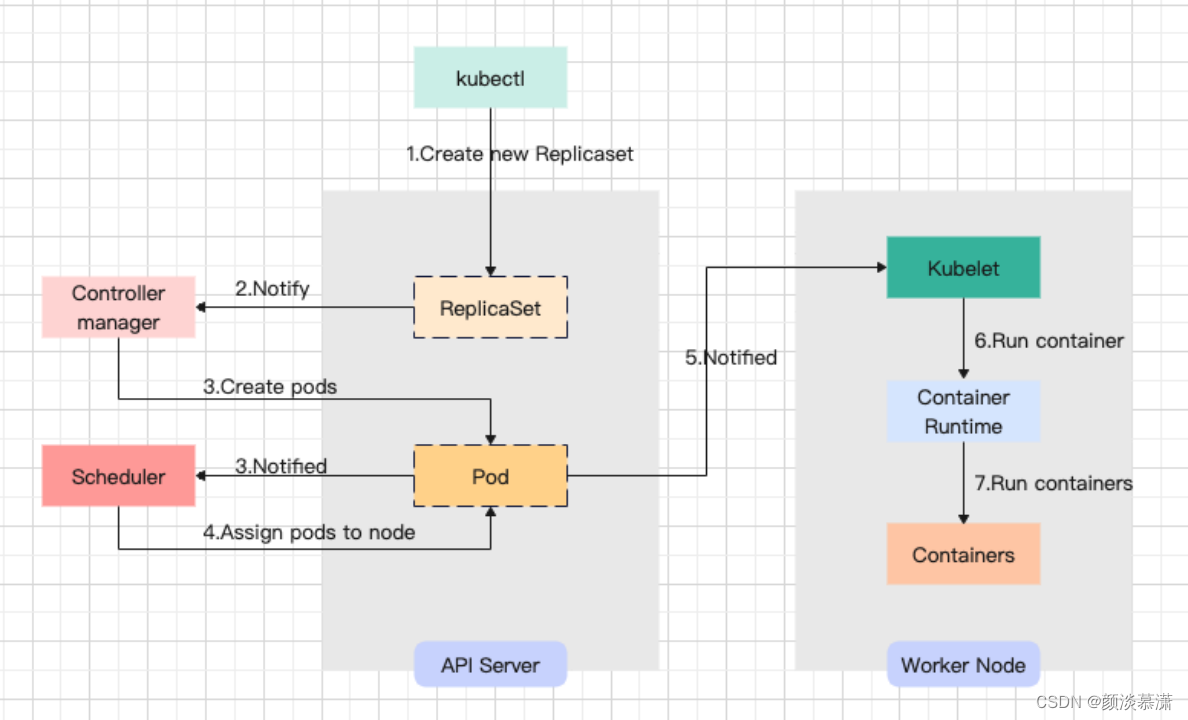
目录 序言 问题 1. 简单说一下k8s集群内外网络如何互通的吧 2.描述一下pod的创建过程 3. 描述一下k8s pod的终止过程 4.Kubernetes 中的自动伸缩有哪些方式？ 5.Kubernetes 中的故障检测有哪些方式？ 6.Kubernetes 中的资源调度有哪些方式ÿ…...
字符函数和字符串函数(上)-C语言详解
CSDN的各位友友们你们好,今天千泽为大家带来的是C语言中字符函数和字符串函数的详解,掌握了这些内容能够让我们更加灵活的运用字符串,接下来让我们一起走进今天的内容吧!写这篇文章需要在cplusplus.com上大量截图,十分不易!如果对您有帮助的话希望能够得到您的支持和帮助,我会持…...
全连接神经网络
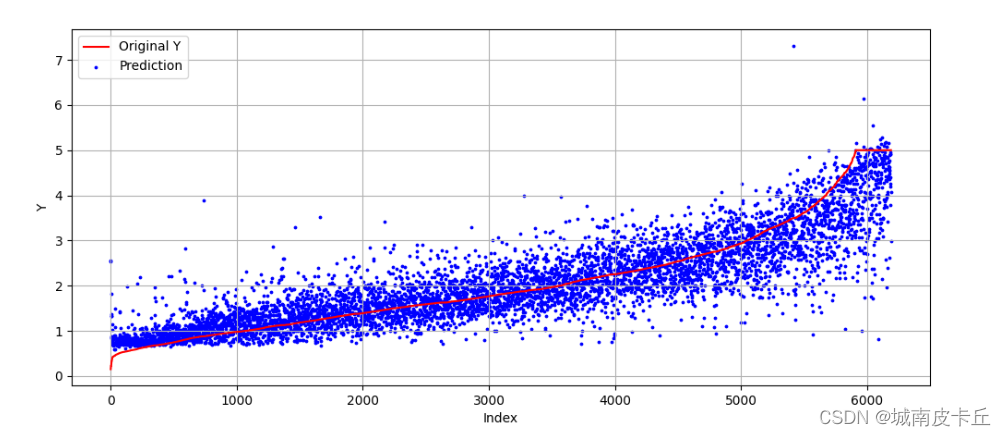
目录 1.全连接神经网络简介 2.MLP分类模型 2.1 数据准备与探索 2.2 搭建网络并可视化 2.3 使用未预处理的数据训练模型 2.4 使用预处理后的数据进行模型训练 3. MLP回归模型 3.1 数据准备 3.2 搭建回归预测网络 1.全连接神经网络简介 全连接神经网络(Multi-Layer Percep…...
深度学习目标检测ui界面-交通标志检测识别
深度学习目标检测ui界面-交通标志检测识别 为了将算法封装起来，博主尝试了实验pyqt5的上位机界面进行封装，其中遇到了一些坑举给大家避开。这里加载的训练模型参考之前写的博客： 自动驾驶目标检测项目实战(一)—基于深度学习框架yolov的交通…...
ubuntu不同版本的源（换源）（镜像源）（lsb_release -c命令，显示当前系统的发行版代号（Codename））
文章目录查看unbuntu版本名（lsb_release -c命令）各个版本源代号（仅供参考，具体代号用上面命令查）各版本软件源Ubuntu20.10阿里源：清华源：Ubuntu20.04阿里源：清华源：Ubunt…...
linux入门---程序翻译的过程
我们在vs编译器中写的代码按下ctrl f5就可以直接运行起来，并且会将运行的结果显示到显示器上，这里看上去只有一个步骤但实际上这里会存在很多的细节，比如说生成结果在这里插入代码片之前我们的代码会经过预处理，编译，汇…...
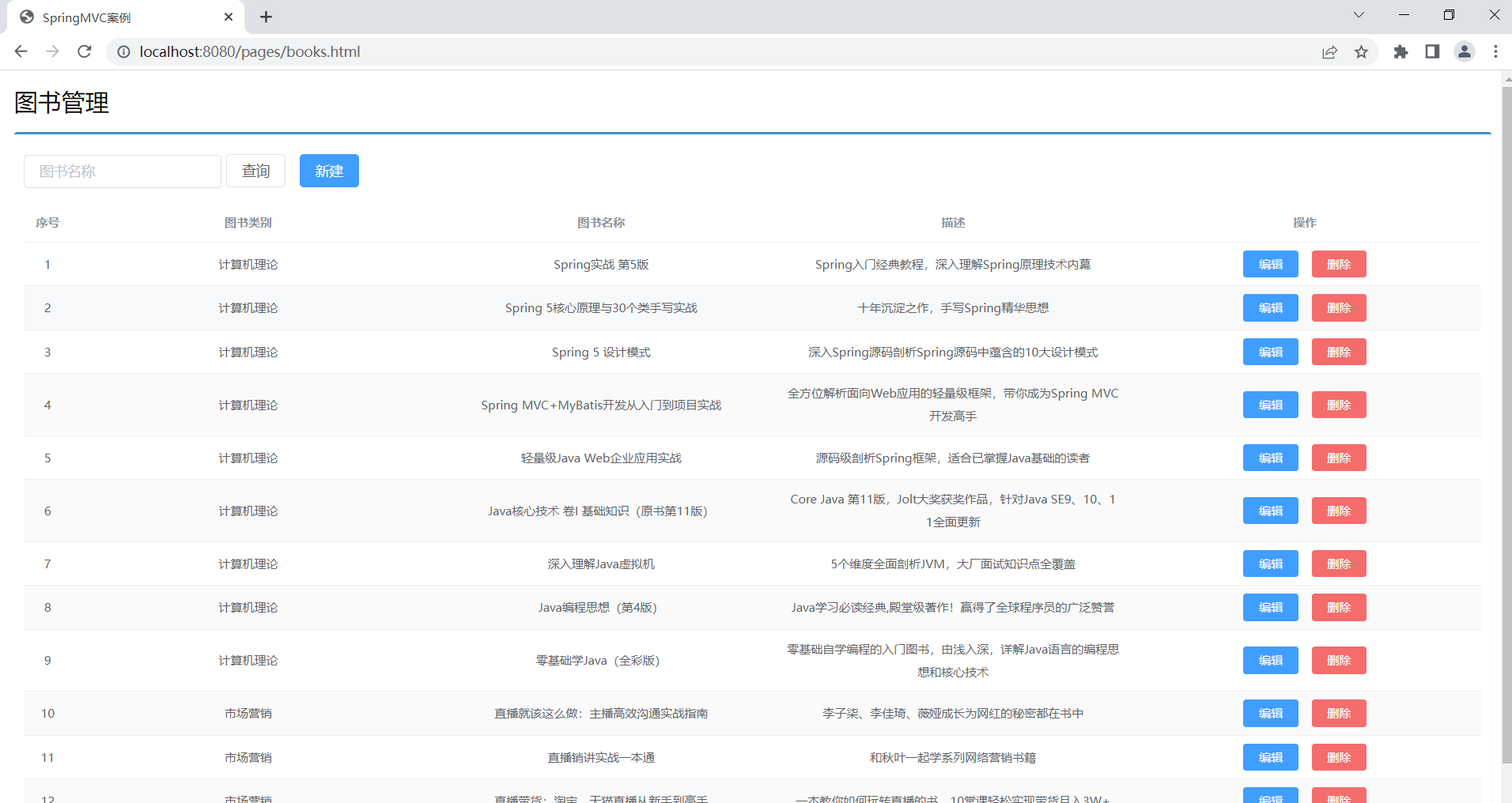
springboot复习（黑马）
学习目标基于SpringBoot框架的程序开发步骤熟练使用SpringBoot配置信息修改服务器配置基于SpringBoot的完成SSM整合项目开发一、SpringBoot简介1. 入门案例问题导入SpringMVC的HelloWord程序大家还记得吗？SpringBoot是由Pivotal团队提供的全新框架，其设计…...
C++指针详解
旧文更新：两三年的旧文了，一直放在电脑里，现在直接传上CSDN 一、指针的概念 1.1 指针 程序运行时每个变量都会有一块内存空间，变量的值就存放在这块空间中。程序可以通过变量名直接访问这块空间内的数据，这种访问方…...
tauri+vite+vue3开发环境下创建、启动运行和打包发布
目录 1.创建项目 2.安装依赖 3.启动项目 4.打包生成windows安装包 5.安装打包生成的安装包 1.创建项目 运行下面命令创建一个tauri项目 pnpm create tauri-app 我创建该项目时的node版本为16.15.0 兼容性注意 Vite 需要 Node.js 版本 14.18，16。然而&#x…...
安卓进阶系列-系统基础
文章目录计算机结构冯诺依曼结构哈弗结构冯诺依曼结构与哈弗结构对比安卓采用的架构安卓操作系统进程间通讯（IPC）内存共享linux内存共享安卓内存共享管道Unix Domain Socket同步常见同步机制信号量Mutex管程安卓同步机制安卓中的Mutex安卓中的ConditionB…...
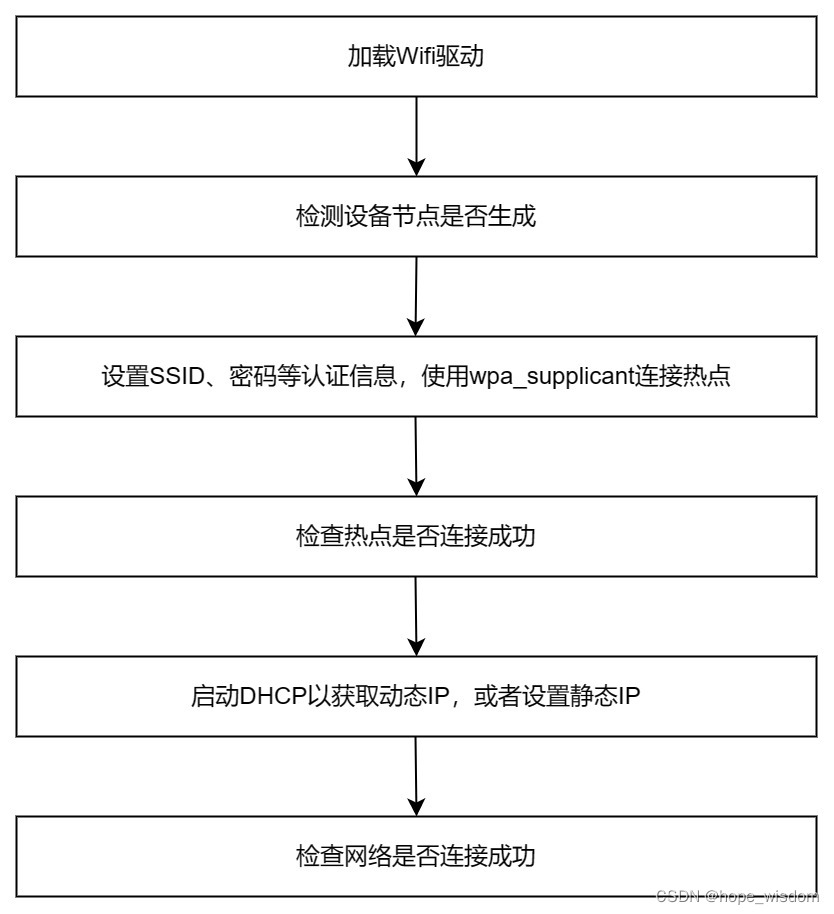
10 Wifi网络的封装
概述 Wifi有多种工作模式，比如：STA模式、AccessPoint模式、Monitor模式、Ad-hoc模式、Mesh模式等。但在IPC设备上，主要使用STA和AccessPoint这两种模式。下面分别进行介绍。 STA模式：任何一种无线网卡都可以运行在此模式，这种模式也是无线网卡的默认模式。在此模式下，无线…...
手把手的教你安装PyCharm --Pycharm安装详细教程（一）（非常详细，非常实用）
简介 Jetbrains家族和Pycharm版本划分： pycharm是Jetbrains家族中的一个明星产品，Jetbrains开发了许多好用的编辑器，包括Java编辑器（IntelliJ IDEA）、JavaScript编辑器（WebStorm）、PHP编辑器&…...
开发板与ubantu文件传送
接下来的所以实验都通过下面这种方式发送APP文件到开发板运行 目录 1、在ubantu配置 ①在虚拟机上添加一个桥接模式的虚拟网卡 ②设定网卡 ③在网卡上配置静态地址 2、开发板设置 ①查看网卡 ②配置网卡静态ip 3、 测试 ①ping ②文件传送 传送报错情况 配置环境&#…...
Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...
在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中，时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志，到供应链系统的物流节点时间戳，时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库，其日期时间类型的…...
Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机：Ubuntu 20.04.6 LTSHost：ARM32位交叉编译器：arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...
从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略，并且实现了基本的选区操作，还调研了自绘选区的实现。那么相对的，我们还需要设计编辑器的选区表达，也可以称为模型选区。编辑器中应用变更时的操作范围，就是以模型选区为基准来…...
ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...
鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建： 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建： File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...
将对透视变换后的图像使用Otsu进行阈值化，来分离黑色和白色像素。这句话中的Otsu是什么意思？
Otsu 是一种自动阈值化方法，用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理，能够自动确定一个阈值，将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...
论文解读：交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架（一）
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读：交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架（一） 论文解读：交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...
省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
数学建模-滑翔伞伞翼面积的设计，运动状态计算和优化 ！
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态，并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...