letcode 4.寻找两个正序数组的中位数(官方题解笔记)
题目描述
给定两个大小分别为
m和n的正序(从小到大)数组nums1和nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为
O(log (m+n))。
1.二分查找
1.1思路
时间复杂度:O(log(m+n))
空间复杂度:O(1)
给定两个有序数组,要求找到两个有序数组的中位数,最直观的思路有以下两种:
(1)使用归并的方式,合并两个有序数组,得到一个大的有序数组。大的有序数组的中间位置的元素,即为中位数。
(2)不需要合并两个有序数组,只要找到中位数的位置即可。由于两个数组的长度已知,因此中位数对应的两个数组的下标之和也是已知的。维护两个指针,初始时分别指向两个数组的下标0的位置,每次将指向较小值的指针后移一位(如果一个指针已经到达数组末尾,则只需要移动另一个数组的指针),直到到达中位数的位置。
假设两个有序数组的长度分别为
m和n,上述两种思路的复杂度如何?
第一种思路的时间复杂度是
O(m+n),空间复杂度是O(m+n)。第二种思路虽然可以将空间复杂度降到O(1),但是时间复杂度仍是O(m+n)。
如何把时间复杂度降低到
O(log(m+n))呢?如果对时间复杂度的要求有log,通常都需要用到二分查找,这道题也可以通过二分查找实现。
根据中位数的定义,当
m+n是奇数时,中位数是两个有序数组中的第(m+n)/2个元素,当m+n是偶数时,中位数是两个有序数组中的第(m+n)/2个元素和第(m+n)/2+1个元素的平均值。因此,这道题可以转化成寻找两个有序数组中的第k小的数,其中k为(m+n)/2或(m+n)/2+1。
假设两个有序数组分别是
A和B。要找到第k个元素,我们可以比较A[k/2−1]和B[k/2−1],其中/表示整数除法。由于A[k/2−1]和B[k/2−1]的前面分别有A[0..k/2−2]和B[0..k/2−2],即k/2−1个元素,对于A[k/2−1]和B[k/2−1]中的较小值,最多只会有(k/2−1)+(k/2−1)≤k−2个元素比它小,那么它就不能是第k小的数了。
因此我们可以归纳出三种情况:
(1)如果
A[k/2−1]<B[k/2−1],则比A[k/2−1]小的数最多只有A的前k/2−1个数和B的前k/2−1个数,即比A[k/2−1]小的数最多只有k−2个,因此A[k/2−1]不可能是第k个数,A[0]到A[k/2−1]也都不可能是第k个数,可以全部排除。
(2)如果A[k/2−1]>B[k/2−1],则可以排除B[0]到B[k/2−1]。
(3)如果A[k/2−1]=B[k/2−1],则可以归入第一种情况处理。

可以看到,比较
A[k/2−1]和B[k/2−1]之后,可以排除k/2个不可能是第k小的数,查找范围缩小了一半。同时,我们将在排除后的新数组上继续进行二分查找,并且根据我们排除数的个数,减少k的值,这是因为我们排除的数都不大于第k小的数。
有以下三种情况需要特殊处理:
(1)如果
A[k/2−1]或者B[k/2−1]越界,那么我们可以选取对应数组中的最后一个元素。在这种情况下,我们必须根据排除数的个数减少k的值,而不能直接将k减去k/2。
(2)如果一个数组为空,说明该数组中的所有元素都被排除,我们可以直接返回另一个数组中第k小的元素。
(3)如果k=1,我们只要返回两个数组首元素的最小值即可。
1.一个例子
用一个例子说明上述算法。假设两个有序数组如下:
A: 1 3 4 9
B: 1 2 3 4 5 6 7 8 9
两个有序数组的长度分别是
4和9,长度之和是13,中位数是两个有序数组中的第7个元素,因此需要找到第k=7个元素。
比较两个有序数组中下标为
k/2−1=2的数,即A[2]和B[2],如下面所示:
A: 1 3 4 9↑
B: 1 2 3 4 5 6 7 8 9↑
由于
A[2]>B[2],因此排除B[0]到B[2],即数组B的下标偏移offset变为3,同时更新k的值:k=k−k/2=4。
下一步寻找,比较两个有序数组中下标为
k/2−1=1的数,即A[1]和B[4],如下面所示,其中方括号部分表示已经被排除的数。
A: 1 3 4 9↑
B: [1 2 3] 4 5 6 7 8 9↑
由于
A[1]<B[4],因此排除A[0]到A[1],即数组A的下标偏移变为2,同时更新k的值:k=k−k/2=2。
下一步寻找,比较两个有序数组中下标为
k/2−1=0的数,即比较A[2]和B[3],如下面所示,其中方括号部分表示已经被排除的数。
A: [1 3] 4 9↑
B: [1 2 3] 4 5 6 7 8 9↑
由于
A[2]=B[3],根据之前的规则,排除A中的元素,因此排除A[2],即数组A的下标偏移变为3,同时更新k的值:k=k−k/2=1。
由于
k的值变成1,因此比较两个有序数组中的未排除下标范围内的第一个数,其中较小的数即为第k个数,由于A[3]>B[3],因此第k个数是B[3]=4。
A: [1 3 4] 9↑
B: [1 2 3] 4 5 6 7 8 9↑
1.2代码
1.C++
class Solution {
public:// 此函数作用:寻找两有序数组 nums1 和 nums2 中第 k 小的数并返回该数int getKthElement(const vector<int>& nums1, const vector<int>& nums2, int k) {/* 主要思路:要找到第 k (k>1) 小的元素,那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较* 这里的 "/" 表示整除* nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个* nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个* 取 pivot = min(pivot1, pivot2),两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个* 这样 pivot 本身最大也只能是第 k-1 小的元素* 如果 pivot = pivot1,那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除",剩下的作为新的 nums1 数组* 如果 pivot = pivot2,那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除",剩下的作为新的 nums2 数组* 由于我们 "删除" 了一些元素(这些元素都比第 k 小的元素要小),因此需要修改 k 的值,减去删除的数的个数*/int m = nums1.size(); // 数组 nums1 的大小int n = nums2.size(); // 数组 nums2 的大小int index1 = 0, index2 = 0; // 数组 nums1 和 nums2 的偏移while (true) {// 边界情况if (index1 == m) { // 数组 nums1 为空return nums2[index2 + k - 1]; // 返回数组 nums2 中第 k 小的数}if (index2 == n) { // 数组 nums2 为空return nums1[index1 + k - 1]; // 返回数组 nums1 中第 k 小的数}if (k == 1) { // 若 k = 1,则返回两个有序数组中的未排除下标范围内的第一个数return min(nums1[index1], nums2[index2]);}// 正常情况int newIndex1 = min(index1 + k / 2 - 1, m - 1); // 数组 nums1 加上偏移后的新下标int newIndex2 = min(index2 + k / 2 - 1, n - 1); // 数组 nums2 加上偏移后的新下标int pivot1 = nums1[newIndex1]; // 数组 nums1 中参与比较的值int pivot2 = nums2[newIndex2]; // 数组 nums2 中参与比较的值if (pivot1 <= pivot2) { // 若 A[k/2-1] <= B[k/2-1]k -= newIndex1 - index1 + 1; // 更新 k = k - k / 2index1 = newIndex1 + 1; // 更新数组 nums1 的偏移值}else { // 若 B[k/2-1] < A[k/2-1]k -= newIndex2 - index2 + 1; // 更新 k = k - k / 2index2 = newIndex2 + 1; // 更新数组 nums2 的偏移值}}}double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {int totalLength = nums1.size() + nums2.size(); // 两数组总长if (totalLength % 2 == 1) { // 若总长为奇数// 第 k 小的数即为中位数return getKthElement(nums1, nums2, (totalLength + 1) / 2);}else { // 若总长为偶数// 中位数 = (第 k 小的数 + 第 [k + 1] 的数) / 2return (getKthElement(nums1, nums2, totalLength / 2) + getKthElement(nums1, nums2, totalLength / 2 + 1)) / 2.0;}}
};
2.Python3
class Solution:def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:# 此函数作用:寻找两有序数组 nums1 和 nums2 中第 k 小的数并返回该数def getKthElement(k):"""- 主要思路:要找到第 k (k>1) 小的元素,那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较- 这里的 "/" 表示整除- nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个- nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个- 取 pivot = min(pivot1, pivot2),两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个- 这样 pivot 本身最大也只能是第 k-1 小的元素- 如果 pivot = pivot1,那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除",剩下的作为新的 nums1 数组- 如果 pivot = pivot2,那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除",剩下的作为新的 nums2 数组- 由于我们 "删除" 了一些元素(这些元素都比第 k 小的元素要小),因此需要修改 k 的值,减去删除的数的个数"""index1, index2 = 0, 0 # 数组 nums1 和 nums2 的偏移while True:# 特殊情况if index1 == m: # 数组 nums1 为空return nums2[index2 + k - 1] # 返回数组 nums2 中第 k 小的数if index2 == n: # 数组 nums2 为空return nums1[index1 + k - 1] # 返回数组 nums1 中第 k 小的数if k == 1: # 若 k = 1,则返回两个有序数组中的未排除下标范围内的第一个数return min(nums1[index1], nums2[index2])# 正常情况newIndex1 = min(index1 + k // 2 - 1, m - 1) # 数组 nums1 加上偏移后的新下标newIndex2 = min(index2 + k // 2 - 1, n - 1) # 数组 nums2 加上偏移后的新下标pivot1, pivot2 = nums1[newIndex1], nums2[newIndex2] # 数组 nums1,nums2 中参与比较的值if pivot1 <= pivot2: # 若 A[k/2-1] <= B[k/2-1]k -= newIndex1 - index1 + 1 # 更新 k = k - k / 2index1 = newIndex1 + 1 # 更新数组 nums1 的偏移值else: # 若 B[k/2-1] < A[k/2-1]k -= newIndex2 - index2 + 1 # 更新 k = k - k / 2index2 = newIndex2 + 1 # 更新数组 nums1 的偏移值m, n = len(nums1), len(nums2) # 数组 nums1,nums2 的长度totalLength = m + n # 数组 nums1,nums2 的总长度if totalLength % 2 == 1: # 若总长度为奇数return getKthElement((totalLength + 1) // 2) # 第 k 小的数即为中位数else: # 若总长为偶数# 中位数 = (第 k 小的数 + 第 [k + 1] 的数) / 2return (getKthElement(totalLength // 2) + getKthElement(totalLength // 2 + 1)) / 2
3.Java
class Solution {public double findMedianSortedArrays(int[] nums1, int[] nums2) {int length1 = nums1.length, length2 = nums2.length;int totalLength = length1 + length2;if (totalLength % 2 == 1) {int midIndex = totalLength / 2;double median = getKthElement(nums1, nums2, midIndex + 1);return median;} else {int midIndex1 = totalLength / 2 - 1, midIndex2 = totalLength / 2;double median = (getKthElement(nums1, nums2, midIndex1 + 1) + getKthElement(nums1, nums2, midIndex2 + 1)) / 2.0;return median;}}public int getKthElement(int[] nums1, int[] nums2, int k) {/* 主要思路:要找到第 k (k>1) 小的元素,那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较* 这里的 "/" 表示整除* nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个* nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个* 取 pivot = min(pivot1, pivot2),两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个* 这样 pivot 本身最大也只能是第 k-1 小的元素* 如果 pivot = pivot1,那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除",剩下的作为新的 nums1 数组* 如果 pivot = pivot2,那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除",剩下的作为新的 nums2 数组* 由于我们 "删除" 了一些元素(这些元素都比第 k 小的元素要小),因此需要修改 k 的值,减去删除的数的个数*/int length1 = nums1.length, length2 = nums2.length;int index1 = 0, index2 = 0;int kthElement = 0;while (true) {// 边界情况if (index1 == length1) {return nums2[index2 + k - 1];}if (index2 == length2) {return nums1[index1 + k - 1];}if (k == 1) {return Math.min(nums1[index1], nums2[index2]);}// 正常情况int half = k / 2;int newIndex1 = Math.min(index1 + half, length1) - 1;int newIndex2 = Math.min(index2 + half, length2) - 1;int pivot1 = nums1[newIndex1], pivot2 = nums2[newIndex2];if (pivot1 <= pivot2) {k -= (newIndex1 - index1 + 1);index1 = newIndex1 + 1;} else {k -= (newIndex2 - index2 + 1);index2 = newIndex2 + 1;}}}
}
4.Golang
func findMedianSortedArrays(nums1 []int, nums2 []int) float64 {totalLength := len(nums1) + len(nums2)if totalLength%2 == 1 {midIndex := totalLength/2return float64(getKthElement(nums1, nums2, midIndex + 1))} else {midIndex1, midIndex2 := totalLength/2 - 1, totalLength/2return float64(getKthElement(nums1, nums2, midIndex1 + 1) + getKthElement(nums1, nums2, midIndex2 + 1)) / 2.0}return 0
}func getKthElement(nums1, nums2 []int, k int) int {index1, index2 := 0, 0for {if index1 == len(nums1) {return nums2[index2 + k - 1]}if index2 == len(nums2) {return nums1[index1 + k - 1]}if k == 1 {return min(nums1[index1], nums2[index2])}half := k/2newIndex1 := min(index1 + half, len(nums1)) - 1newIndex2 := min(index2 + half, len(nums2)) - 1pivot1, pivot2 := nums1[newIndex1], nums2[newIndex2]if pivot1 <= pivot2 {k -= (newIndex1 - index1 + 1)index1 = newIndex1 + 1} else {k -= (newIndex2 - index2 + 1)index2 = newIndex2 + 1}}return 0
}func min(x, y int) int {if x < y {return x}return y
}
2.划分数组
2.1思路
时间复杂度:O(log(min(m,n)))
空间复杂度:O(1)
二分查找的时间复杂度已经很优秀了,但本题存在时间复杂度更低的一种方法。这里给出推导过程,勇于挑战自己的读者可以进行尝试。
为了使用划分的方法解决这个问题,需要理解「中位数的作用是什么」。在统计中,中位数被用来:
将一个集合划分为两个长度相等的子集,其中一个子集中的元素总是大于另一个子集中的元素。
如果理解了中位数的划分作用,就很接近答案了。
首先,在任意位置
i将A划分成两个部分:
left_A | right_AA[0], A[1], ..., A[i-1] | A[i], A[i+1], ..., A[m-1]
由于
A中有m个元素, 所以有m+1种划分的方法i∈[0,m]。其中
len(left_A)=i,len(right_A)=m−i.
注意:当
i=0时,left_A为空集, 而当i=m时,right_A为空集。
采用同样的方式,在任意位置
j将B划分成两个部分:
left_B | right_BB[0], B[1], ..., B[j-1] | B[j], B[j+1], ..., B[n-1]
将
left_A和left_B放入一个集合,并将right_A和right_B放入另一个集合。 再把这两个新的集合分别命名为left_part和right_part:
left_part | right_partA[0], A[1], ..., A[i-1] | A[i], A[i+1], ..., A[m-1]B[0], B[1], ..., B[j-1] | B[j], B[j+1], ..., B[n-1]
当
A和B的总长度是偶数时,如果可以确认:
len(left_part)=len(right_part)
max(left_part)≤min(right_part)
那么,
{A,B}中的所有元素已经被划分为相同长度的两个部分,且前一部分中的元素总是小于或等于后一部分中的元素。中位数就是前一部分的最大值和后一部分的最小值的平均值:
median = [max(left_part) + min(right_part)] / 2
当 A 和 B 的总长度是奇数时,如果可以确认:
len(left_part)=len(right_part)+1
max(left_part)≤min(right_part)
那么,
{A,B}中的所有元素已经被划分为两个部分,前一部分比后一部分多一个元素,且前一部分中的元素总是小于或等于后一部分中的元素。中位数就是前一部分的最大值:
median=max(left_part)
第一个条件对于总长度是偶数和奇数的情况有所不同,但是可以将两种情况合并。第二个条件对于总长度是偶数和奇数的情况是一样的。
要确保这两个条件,只需要保证:
(1)
i+j=m−i+n−j(当m+n为偶数)或i+j=m−i+n−j+1(当m+n为奇数)。
等号左侧为前一部分的元素个数,等号右侧为后一部分的元素个数。
将i和j全部移到等号左侧,我们就可以得到i + j = (m + n + 1) / 2。
这里的分数结果只保留整数部分。
(2)0≤i≤m,0≤j≤n。如果我们规定A的长度小于等于B的长度,即m≤n。
这样对于任意的i∈[0,m],都有j = (m + n + 1) / 2 - i ∈ [0,n],那么我们在[0,m]的范围内枚举i并得到j,就不需要额外的性质了。如果
A的长度较大,那么我们只要交换A和B即可。
如果m>n,那么得出的j有可能是负数。
(3)
B[j−1]≤A[i]以及A[i−1]≤B[j],即前一部分的最大值小于等于后一部分的最小值。
为了简化分析,假设
A[i−1],B[j−1],A[i],B[j]总是存在。
对于i=0、i=m、j=0、j=n这样的临界条件,我们只需要规定A[−1]=B[−1]=−∞,A[m]=B[n]=∞即可。
这也是比较直观的:当一个数组不出现在前一部分时,对应的值为负无穷,就不会对前一部分的 最大值 产生影响;
当一个数组不出现在后一部分时,对应的值为正无穷,就不会对后一部分的 最小值 产生影响。
所以我们需要做的是:
在
[0,m]中找到i,使得:
B[j−1]≤A[i]且A[i−1]≤B[j],其中j = (m + n + 1) / 2 - i
我们证明它等价于:
在
[0,m]中找到最大的i,使得:A[i−1]≤B[j],其中j = (m + n + 1) / 2 - i
这是因为:
当
i从0∼m递增时,A[i−1]递增,B[j]递减,所以一定存在一个最大的i满足A[i−1]≤B[j];
如果i是最大的,那么说明i+1不满足。将i+1带入可以得到A[i]>B[j−1],也就是B[j−1]<A[i],就和我们进行等价变换前i的性质一致了(甚至还要更强)。
因此我们可以对
i在[0,m]的区间上进行 二分搜索,找到最大的满足A[i−1]≤B[j]的i值,就得到了划分的方法。此时,划分前一部分元素中的最大值,以及划分后一部分元素中的最小值,才可能作为就是这两个数组的中位数。
2.2代码
1.C++
class Solution {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {if (nums1.size() > nums2.size()) { // 如果数组 nums1 的长度更长return findMedianSortedArrays(nums2, nums1);}int m = nums1.size(); // nums1 的大小int n = nums2.size(); // nums2 的大小int left = 0, right = m; // nums1 的左右边界// median1:前一部分的最大值// median2:后一部分的最小值int median1 = 0, median2 = 0;while (left <= right) {// 前一部分包含 nums1[0 .. i-1] 和 nums2[0 .. j-1]// 后一部分包含 nums1[i .. m-1] 和 nums2[j .. n-1]int i = (left + right) / 2; // 二分搜索满足条件的 i,此为初值int j = (m + n + 1) / 2 - i; // 基于 i + j = (m + n + 1) / 2// nums_im1, nums_i, nums_jm1, nums_j 分别表示 nums1[i-1], nums1[i], nums2[j-1], nums2[j]int nums_im1 = (i == 0 ? INT_MIN : nums1[i - 1]); // i = 0 的情况,i - 1 为负无穷int nums_i = (i == m ? INT_MAX : nums1[i]); // i = m 的情况,i 正无穷int nums_jm1 = (j == 0 ? INT_MIN : nums2[j - 1]); // j = 0 的情况,j - 1 为负无穷int nums_j = (j == n ? INT_MAX : nums2[j]); // j = n 的情况,j 正无穷if (nums_im1 <= nums_j) { // nums1[i - 1] <= nums2[j] 的情况median1 = max(nums_im1, nums_jm1); // 前一部分的最大值:max(nums1[i - 1],nums2[j - 1])median2 = min(nums_i, nums_j); // 后一部分的最小值:min(nums1[i],nums2[j])left = i + 1; // 更新左边界} else { // nums1[i - 1] > nums2[j] 的情况right = i - 1; // 更新右边界}}// 根据两个数组的总长度的奇偶情况决定最后返回的中位数return (m + n) % 2 == 0 ? (median1 + median2) / 2.0 : median1;}
};
2.Python3
class Solution:def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:if len(nums1) > len(nums2): # 如果数组 nums1 的长度更长return self.findMedianSortedArrays(nums2, nums1)infinty = 2**40 # 定义无穷值m, n = len(nums1), len(nums2) # 数组 nums1 和数组 nums2 的长度left, right = 0, m # 数组 nums1 的左右边界# median1:前一部分的最大值# median2:后一部分的最小值median1, median2 = 0, 0while left <= right: # 二分查找目标 i# 前一部分包含 nums1[0 .. i-1] 和 nums2[0 .. j-1]# // 后一部分包含 nums1[i .. m-1] 和 nums2[j .. n-1]i = (left + right) // 2j = (m + n + 1) // 2 - i # 基于 i + j = (m + n + 1) / 2# nums_im1, nums_i, nums_jm1, nums_j 分别表示 nums1[i-1], nums1[i], nums2[j-1], nums2[j]nums_im1 = (-infinty if i == 0 else nums1[i - 1]) # 根据 i 的值确定 nums[i - 1] 的值,若 i = 0,则为负无穷nums_i = (infinty if i == m else nums1[i]) # 根据 i 的值确定 nums[i] 的值,若 i = m,则为正无穷nums_jm1 = (-infinty if j == 0 else nums2[j - 1]) # 根据 j 的值确定 nums[j - 1] 的值,若 j = 0,则为负无穷nums_j = (infinty if j == n else nums2[j]) # 根据 j 的值确定 nums[j] 的值,若 j = n,则为正无穷if nums_im1 <= nums_j: # nums1[i - 1] <= nums2[j] 的情况# 前一部分的最大值:max(nums1[i - 1],nums2[j - 1]),后一部分的最小值:min(nums1[i],nums2[j])median1, median2 = max(nums_im1, nums_jm1), min(nums_i, nums_j)left = i + 1 # 更新左边界else:right = i - 1 # 更新右边界# 根据两个数组的总长度的奇偶情况决定最后返回的中位数return (median1 + median2) / 2 if (m + n) % 2 == 0 else median1
3.Java
class Solution {public double findMedianSortedArrays(int[] nums1, int[] nums2) {if (nums1.length > nums2.length) {return findMedianSortedArrays(nums2, nums1);}int m = nums1.length;int n = nums2.length;int left = 0, right = m;// median1:前一部分的最大值// median2:后一部分的最小值int median1 = 0, median2 = 0;while (left <= right) {// 前一部分包含 nums1[0 .. i-1] 和 nums2[0 .. j-1]// 后一部分包含 nums1[i .. m-1] 和 nums2[j .. n-1]int i = (left + right) / 2;int j = (m + n + 1) / 2 - i;// nums_im1, nums_i, nums_jm1, nums_j 分别表示 nums1[i-1], nums1[i], nums2[j-1], nums2[j]int nums_im1 = (i == 0 ? Integer.MIN_VALUE : nums1[i - 1]);int nums_i = (i == m ? Integer.MAX_VALUE : nums1[i]);int nums_jm1 = (j == 0 ? Integer.MIN_VALUE : nums2[j - 1]);int nums_j = (j == n ? Integer.MAX_VALUE : nums2[j]);if (nums_im1 <= nums_j) {median1 = Math.max(nums_im1, nums_jm1);median2 = Math.min(nums_i, nums_j);left = i + 1;} else {right = i - 1;}}return (m + n) % 2 == 0 ? (median1 + median2) / 2.0 : median1;}
}
4.Golang
func findMedianSortedArrays(nums1 []int, nums2 []int) float64 {if len(nums1) > len(nums2) {return findMedianSortedArrays(nums2, nums1)}m, n := len(nums1), len(nums2)left, right := 0, mmedian1, median2 := 0, 0for left <= right {i := (left + right) / 2j := (m + n + 1) / 2 - inums_im1 := math.MinInt32if i != 0 {nums_im1 = nums1[i-1]}nums_i := math.MaxInt32if i != m {nums_i = nums1[i]}nums_jm1 := math.MinInt32if j != 0 {nums_jm1 = nums2[j-1]}nums_j := math.MaxInt32if j != n {nums_j = nums2[j]}if nums_im1 <= nums_j {median1 = max(nums_im1, nums_jm1)median2 = min(nums_i, nums_j)left = i + 1} else {right = i - 1}}if (m + n) % 2 == 0 {return float64(median1 + median2) / 2.0}return float64(median1)
}func max(x, y int) int {if x > y {return x}return y
}func min(x, y int) int {if x < y {return x}return y
}
相关文章:

letcode 4.寻找两个正序数组的中位数(官方题解笔记)
题目描述 给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。 算法的时间复杂度应该为 O(log (mn)) 。 1.二分查找 1.1思路 时间复杂度:O(log(mn)) 空间复杂度:O(1) 给定…...
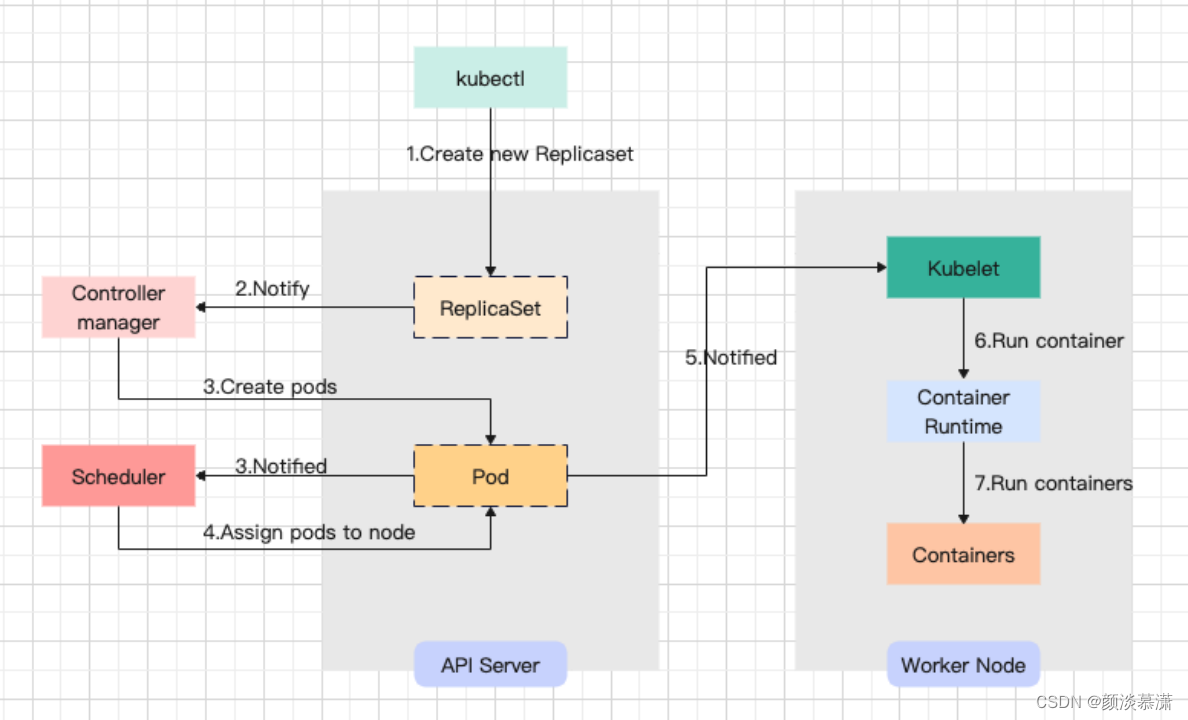
【面试题系列】K8S常见面试题
目录 序言 问题 1. 简单说一下k8s集群内外网络如何互通的吧 2.描述一下pod的创建过程 3. 描述一下k8s pod的终止过程 4.Kubernetes 中的自动伸缩有哪些方式? 5.Kubernetes 中的故障检测有哪些方式? 6.Kubernetes 中的资源调度有哪些方式ÿ…...

字符函数和字符串函数(上)-C语言详解
CSDN的各位友友们你们好,今天千泽为大家带来的是C语言中字符函数和字符串函数的详解,掌握了这些内容能够让我们更加灵活的运用字符串,接下来让我们一起走进今天的内容吧!写这篇文章需要在cplusplus.com上大量截图,十分不易!如果对您有帮助的话希望能够得到您的支持和帮助,我会持…...
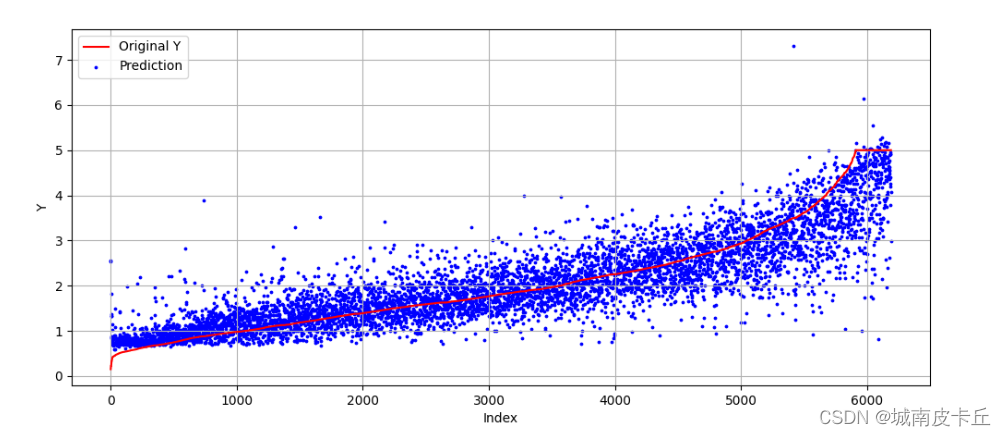
全连接神经网络
目录 1.全连接神经网络简介 2.MLP分类模型 2.1 数据准备与探索 2.2 搭建网络并可视化 2.3 使用未预处理的数据训练模型 2.4 使用预处理后的数据进行模型训练 3. MLP回归模型 3.1 数据准备 3.2 搭建回归预测网络 1.全连接神经网络简介 全连接神经网络(Multi-Layer Percep…...
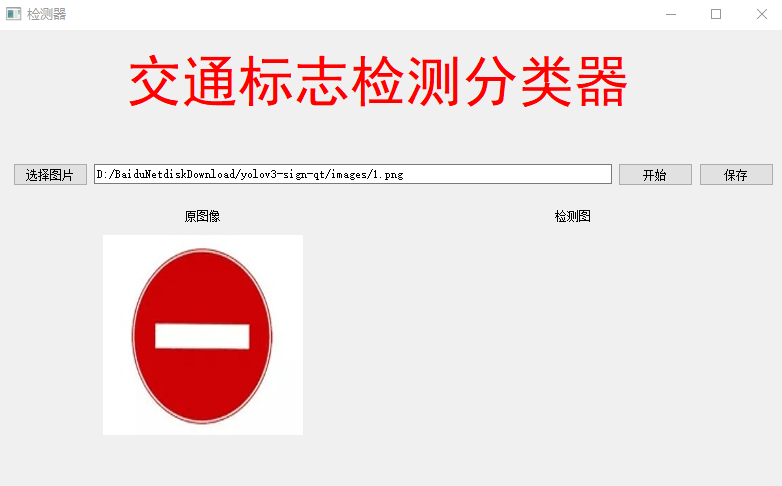
深度学习目标检测ui界面-交通标志检测识别
深度学习目标检测ui界面-交通标志检测识别 为了将算法封装起来,博主尝试了实验pyqt5的上位机界面进行封装,其中遇到了一些坑举给大家避开。这里加载的训练模型参考之前写的博客: 自动驾驶目标检测项目实战(一)—基于深度学习框架yolov的交通…...

ubuntu不同版本的源(换源)(镜像源)(lsb_release -c命令,显示当前系统的发行版代号(Codename))
文章目录查看unbuntu版本名(lsb_release -c命令)各个版本源代号(仅供参考,具体代号用上面命令查)各版本软件源Ubuntu20.10阿里源:清华源:Ubuntu20.04阿里源:清华源:Ubunt…...

linux入门---程序翻译的过程
我们在vs编译器中写的代码按下ctrl f5就可以直接运行起来,并且会将运行的结果显示到显示器上,这里看上去只有一个步骤但实际上这里会存在很多的细节,比如说生成结果在这里插入代码片之前我们的代码会经过预处理,编译,汇…...
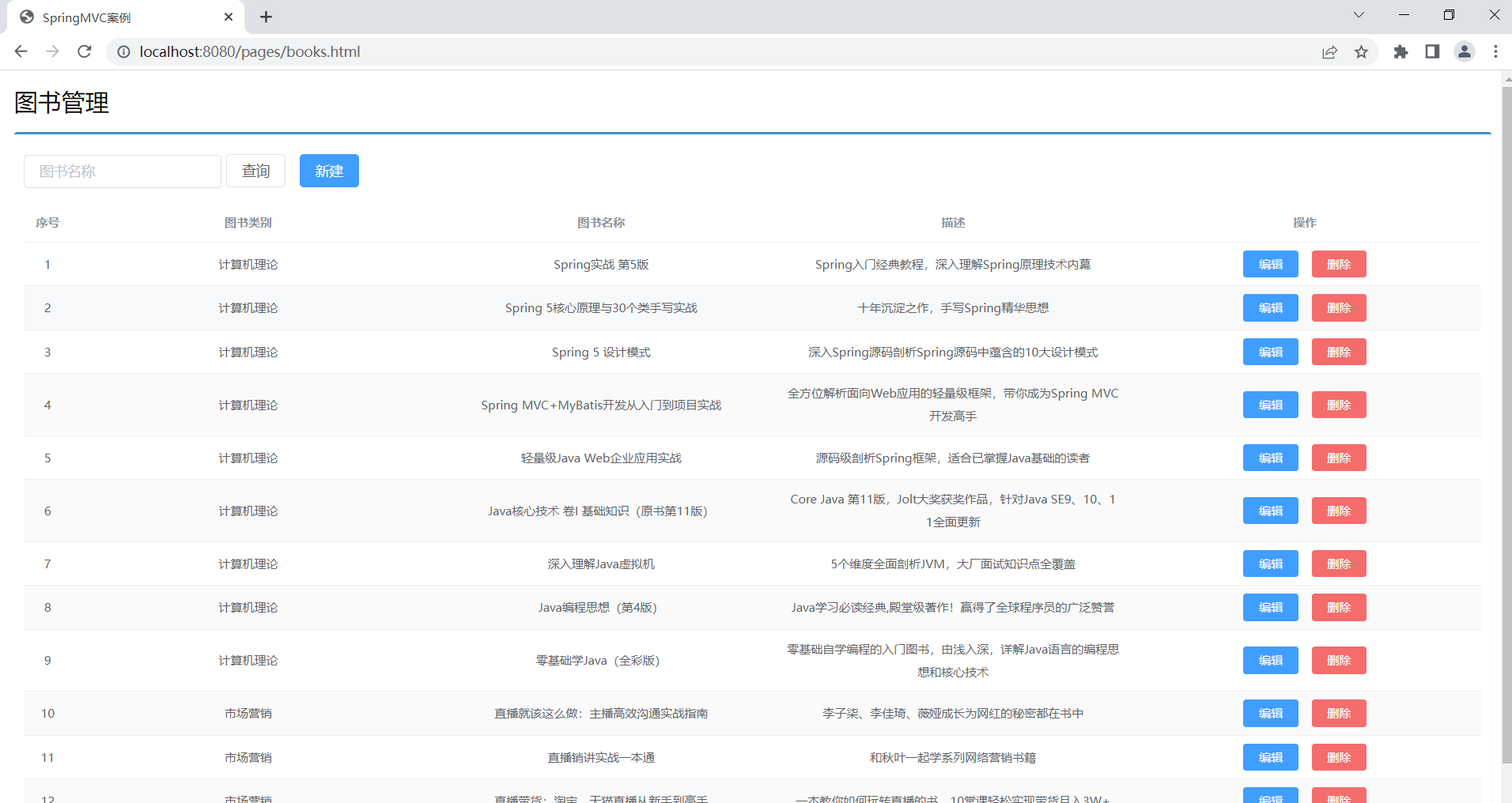
springboot复习(黑马)
学习目标基于SpringBoot框架的程序开发步骤熟练使用SpringBoot配置信息修改服务器配置基于SpringBoot的完成SSM整合项目开发一、SpringBoot简介1. 入门案例问题导入SpringMVC的HelloWord程序大家还记得吗?SpringBoot是由Pivotal团队提供的全新框架,其设计…...

C++指针详解
旧文更新:两三年的旧文了,一直放在电脑里,现在直接传上CSDN 一、指针的概念 1.1 指针 程序运行时每个变量都会有一块内存空间,变量的值就存放在这块空间中。程序可以通过变量名直接访问这块空间内的数据,这种访问方…...
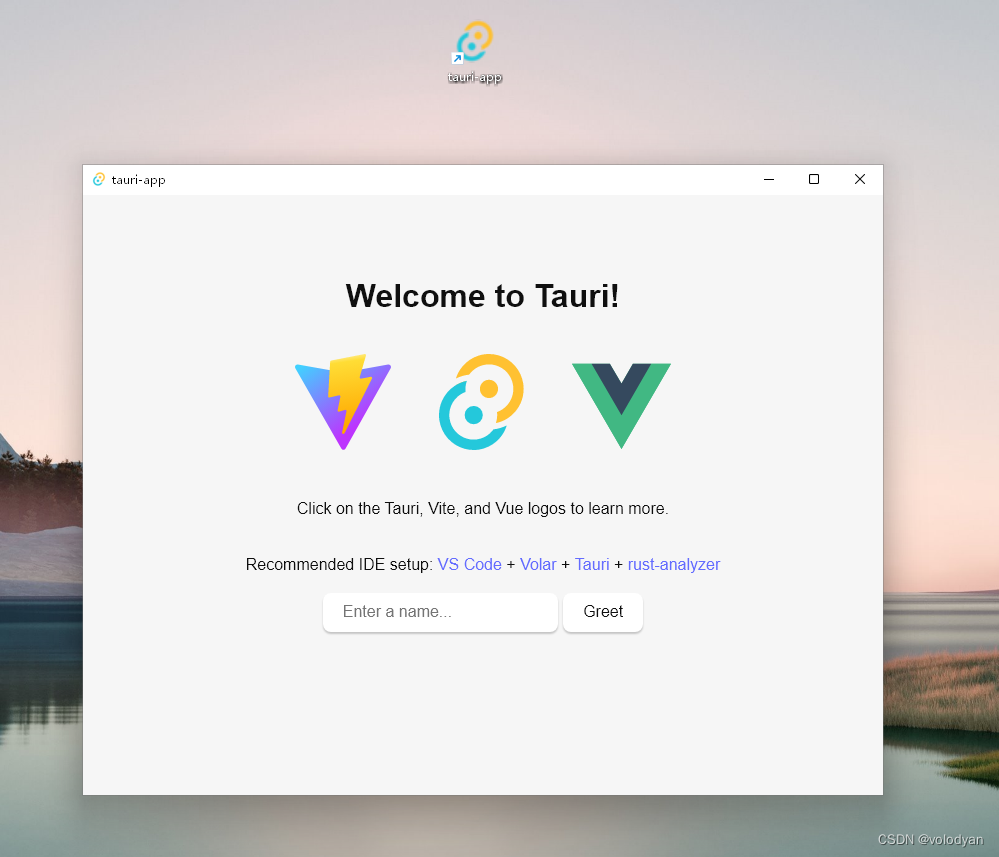
tauri+vite+vue3开发环境下创建、启动运行和打包发布
目录 1.创建项目 2.安装依赖 3.启动项目 4.打包生成windows安装包 5.安装打包生成的安装包 1.创建项目 运行下面命令创建一个tauri项目 pnpm create tauri-app 我创建该项目时的node版本为16.15.0 兼容性注意 Vite 需要 Node.js 版本 14.18,16。然而&#x…...

安卓进阶系列-系统基础
文章目录计算机结构冯诺依曼结构哈弗结构冯诺依曼结构与哈弗结构对比安卓采用的架构安卓操作系统进程间通讯(IPC)内存共享linux内存共享安卓内存共享管道Unix Domain Socket同步常见同步机制信号量Mutex管程安卓同步机制安卓中的Mutex安卓中的ConditionB…...
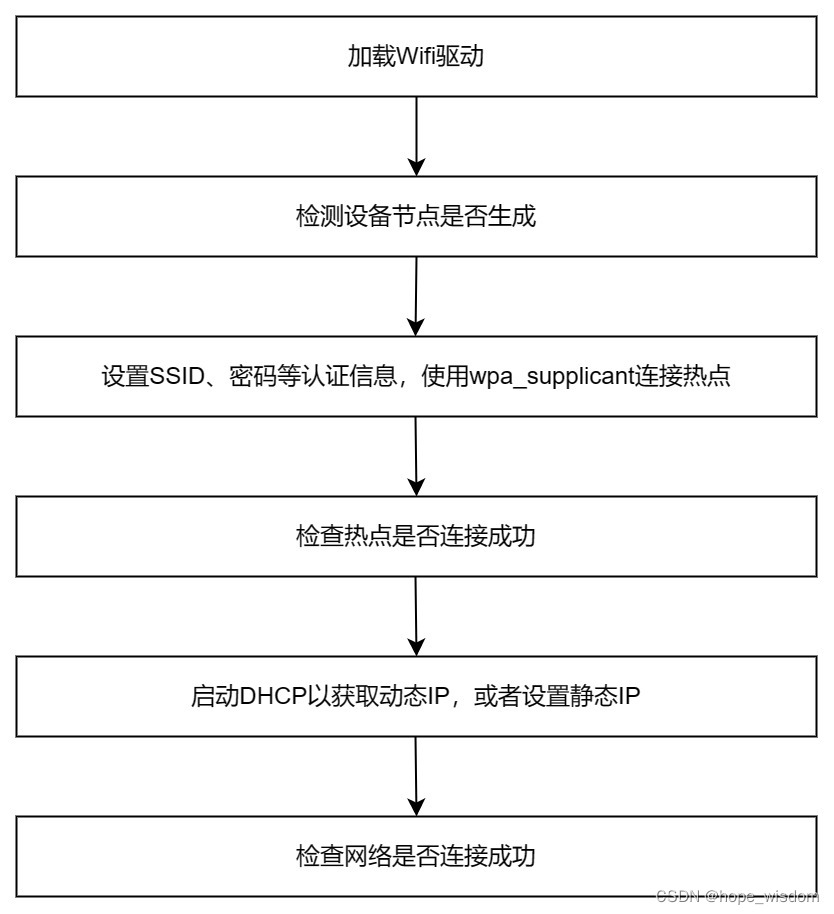
10 Wifi网络的封装
概述 Wifi有多种工作模式,比如:STA模式、AccessPoint模式、Monitor模式、Ad-hoc模式、Mesh模式等。但在IPC设备上,主要使用STA和AccessPoint这两种模式。下面分别进行介绍。 STA模式:任何一种无线网卡都可以运行在此模式,这种模式也是无线网卡的默认模式。在此模式下,无线…...
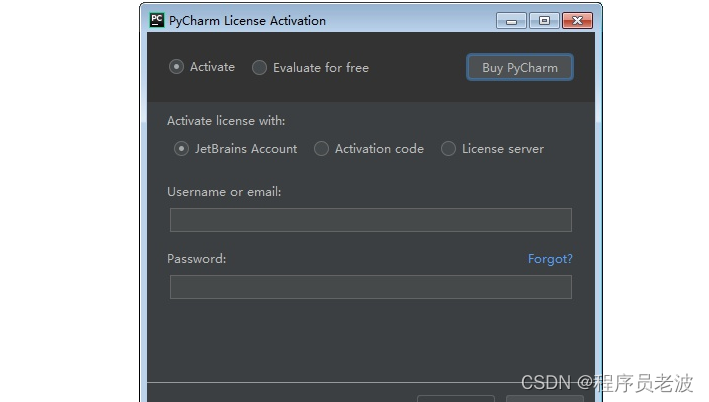
手把手的教你安装PyCharm --Pycharm安装详细教程(一)(非常详细,非常实用)
简介 Jetbrains家族和Pycharm版本划分: pycharm是Jetbrains家族中的一个明星产品,Jetbrains开发了许多好用的编辑器,包括Java编辑器(IntelliJ IDEA)、JavaScript编辑器(WebStorm)、PHP编辑器&…...

开发板与ubantu文件传送
接下来的所以实验都通过下面这种方式发送APP文件到开发板运行 目录 1、在ubantu配置 ①在虚拟机上添加一个桥接模式的虚拟网卡 ②设定网卡 ③在网卡上配置静态地址 2、开发板设置 ①查看网卡 ②配置网卡静态ip 3、 测试 ①ping ②文件传送 传送报错情况 配置环境&#…...
如何成为一名优秀的网络安全工程师?
前言 这是我的建议如何成为网络安全工程师,你应该按照下面顺序学习。 简要说明 第一件事你应该学习如何编程,我建议首先学python,然后是java。 (非必须)接下来学习一些算法和数据结构是很有帮助的,它将…...

面试问题之高并发内存池项目
项目部分 1.这个项目是什么? 高并发内存池的原型是谷歌一个开源项目,tcmalloc,而这个项目,就是tcmalloc中最核心的框架和部分拿出来进行模拟。他的作用就是在去代替原型的内存分配函数malloc和free。这个项目涉及的技术有,c&…...

如果阿里巴巴给蒋凡“百亿补贴”
出品 | 何玺 排版 | 叶媛 2021底,阿里内部进行组织架构大调整,任命蒋凡为阿里海外商业负责人,分管全球速卖通和国际贸易(ICBU)两个海外业务,以及Lazada等面向海外市场的多家子公司。 一年时间过去&#x…...

Linux版本现状
Linux的发行版本可以大体分为两类,一类是商业公司维护的发行版本,一类是社区组织维护的发行版本,前者以著名的Red Hat(RHEL红帽)为代表,后者以Debian为代表。Red HatRedhat,应该称为Redhat系列&…...
)
Winform中实现保存配置到文件/项目启动时从文件中读取配置(序列化与反序列化对象)
场景 Winform中实现序列化指定类型的对象到指定的Xml文件和从指定的Xml文件中反序列化指定类型的对象: Winform中实现序列化指定类型的对象到指定的Xml文件和从指定的Xml文件中反序列化指定类型的对象_winform xml序列化_霸道流氓气质的博客-CSDN博客 上面讲的序…...

基于python的超市历年数据可视化分析
人生苦短 我用python Python其他实用资料:点击此处跳转文末名片获取 数据可视化分析目录人生苦短 我用python一、数据描述1、数据概览二、数据预处理0、导入包和数据1、列名重命名2、提取数据中时间,方便后续分析绘图三、数据可视化1、美国各个地区销售额的分布&…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...
