随机梯度下降 (Stochastic Gradient Descent, SGD)

SGD 是梯度下降法的一种变体。与批量梯度下降法不同，SGD 在每次迭代中仅使用一个样本（或一个小批量样本）的梯度来更新参数。它能更快地更新参数，并且可以更容易地跳出局部最优解。

原理

SGD 的基本思想是通过在每次迭代中使用不同的样本，快速更新参数，并逐步逼近目标函数的最小值。

核心公式

在第 ⅰ次迭代中，选择第 ⅰ个样本 ⅹ(ⅰ) 并计算梯度：

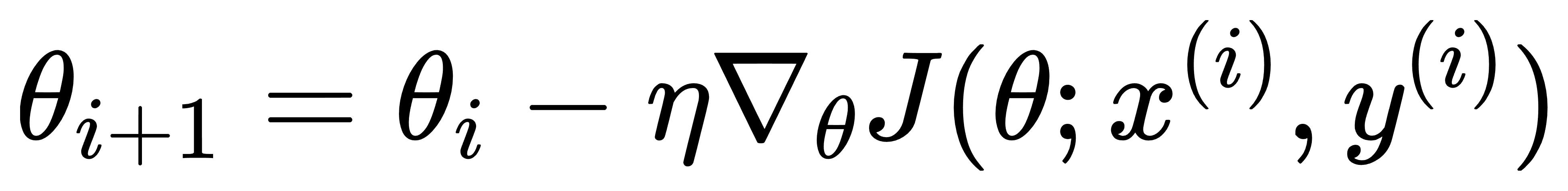
其中：

• θi为第ⅰ次迭代的参数
• η 为学习率
• J( θ; x(i), y(i) )为目标函数在第ⅰ个样本 ⅹ(ⅰ)上的梯度

目标是最小化目标函数 J(θ)，即：

Python 示例

我们将使用Scikit-Learn中的线性回归模型进行训练，并绘制多个数据分析图形。具体的图形包括：损失函数的收敛图、预测结果与实际结果的比较图、以及参数更新的轨迹图。

数据生成和分割

首先，我们生成一个带有噪声的线性回归数据集，并将其划分为训练集和测试集。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import mean_squared_error# 生成回归数据集
X, y = make_regression(n_samples=1000, n_features=1, noise=20, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 打印前5条数据和对应的目标值
print("前5条训练数据：")
print(X_train[:5])
print("前5个训练目标值：")
print(y_train[:5])

SGD 回归模型初始化

使用 SGDRegressor 初始化随机梯度下降回归模型，设定最大迭代次数为1，禁用容忍度检查，启用 warm_start，每次迭代使用上次的解，设定常数学习率和初始学习率。

# 初始化SGD回归模型
sgd = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True, learning_rate='constant', eta0=0.01, random_state=42)

训练模型

进行多次迭代（epochs），在每个 epoch 进行一次模型训练，记录训练误差和测试误差，以及每次迭代后的系数值。

# 记录训练过程中的信息
n_epochs = 50
train_errors, test_errors = [], []
coef_updates = []# 训练模型
for epoch in range(n_epochs):sgd.fit(X_train, y_train)y_train_predict = sgd.predict(X_train)y_test_predict = sgd.predict(X_test)train_errors.append(mean_squared_error(y_train, y_train_predict))test_errors.append(mean_squared_error(y_test, y_test_predict))coef_updates.append(sgd.coef_.copy())

绘制图形

1. 损失函数的收敛图：展示训练误差和测试误差随迭代次数的变化。

# 绘制损失函数的收敛图
plt.figure(figsize=(10, 6))
plt.plot(train_errors, label='训练误差')
plt.plot(test_errors, label='测试误差')
plt.xlabel('迭代次数')
plt.ylabel('均方误差')
plt.title('训练和测试误差随迭代次数的变化')
plt.legend()
plt.grid()
plt.show()

1. 预测结果与实际结果的比较图：展示测试集上的实际值和预测值的散点图。

# 绘制预测结果与实际结果的比较图
plt.figure(figsize=(10, 6))
plt.scatter(X_test, y_test, color='blue', label='实际值')
plt.scatter(X_test, y_test_predict, color='red', label='预测值')
plt.xlabel('输入特征')
plt.ylabel('目标值')
plt.title('实际值与预测值的比较')
plt.legend()
plt.grid()
plt.show()

1. 参数更新的轨迹图：展示模型系数在每个 epoch 的更新情况。

# 绘制参数更新的轨迹图
coef_updates = np.array(coef_updates)
plt.figure(figsize=(10, 6))
plt.plot(coef_updates, marker='o')
plt.xlabel('迭代次数')
plt.ylabel('系数值')
plt.title('系数更新轨迹')
plt.grid()
plt.show()

案例描述

我们将构建一个案例，使用随机梯度下降（SGD）算法对一个带有噪声的线性回归数据集进行训练和预测。具体步骤如下：

1. 生成数据：使用 make_regression 生成一个包含 1000 个样本和 1 个特征的回归数据集，并添加噪声。
2. 数据分割：将数据集划分为训练集和测试集。
3. 初始化模型：使用 SGDRegressor 初始化随机梯度下降回归模型。
4. 模型训练：通过多次迭代（epochs），在每个 epoch 中使用训练数据训练模型，并记录训练误差和测试误差，以及每次迭代后的模型系数。
5. 结果可视化：绘制损失函数的收敛图、预测结果与实际结果的比较图，以及参数更新的轨迹图。

代码实现

以下是实现上述案例的详细代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import mean_squared_error# 生成回归数据集
X, y = make_regression(n_samples=1000, n_features=1, noise=20, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 初始化SGD回归模型
sgd = SGDRegressor(max_iter=1, tol=None, warm_start=True, learning_rate='constant', eta0=0.01, random_state=42)# 记录训练过程中的信息
n_epochs = 50
train_errors, test_errors = [], []
coef_updates = []# 训练模型
for epoch in range(n_epochs):sgd.fit(X_train, y_train)y_train_predict = sgd.predict(X_train)y_test_predict = sgd.predict(X_test)train_errors.append(mean_squared_error(y_train, y_train_predict))test_errors.append(mean_squared_error(y_test, y_test_predict))coef_updates.append(sgd.coef_.copy())# 绘制损失函数的收敛图
plt.figure(figsize=(10, 6))
plt.plot(train_errors, label='Train Error')
plt.plot(test_errors, label='Test Error')
plt.xlabel('Epoch')
plt.ylabel('Mean Squared Error')
plt.title('Training and Test Errors Over Epochs')
plt.legend()
plt.grid()
plt.show()# 绘制预测结果与实际结果的比较图
plt.figure(figsize=(10, 6))
# 使用最后一次迭代的预测结果
plt.scatter(X_test, y_test, color='blue', label='Actual')
plt.scatter(X_test, y_test_predict, color='red', label='Predicted')
plt.xlabel('Input Feature')
plt.ylabel('Target')
plt.title('Actual vs Predicted')
plt.legend()
plt.grid()
plt.show()# 绘制参数更新的轨迹图
coef_updates = np.array(coef_updates)
plt.figure(figsize=(10, 6))
plt.plot(coef_updates, marker='o')
plt.xlabel('Epoch')
plt.ylabel('Coefficient Value')
plt.title('Coefficient Updates Over Epochs')
plt.grid()
plt.show()

详细步骤解释

1. 生成数据：

• • 使用 make_regression 生成一个线性回归数据集，包含 1000 个样本，每个样本有 1 个特征，并添加噪声以模拟真实数据中的误差。
  • 使用 train_test_split 将数据集划分为训练集（80%）和测试集（20%）。

1. 初始化模型：

• • 使用 SGDRegressor 初始化随机梯度下降回归模型，设置 max_iter=1 和 warm_start=True 以确保每次迭代都使用上次的解。
  • 设置常数学习率（learning_rate='constant'）和初始学习率（eta0=0.01）。

1. 模型训练：

• • 进行 50 次迭代（epochs），在每次迭代中使用训练数据训练模型。
  • 记录每次迭代的训练误差和测试误差，以及模型系数。

1. 结果可视化：

• • 损失函数的收敛图：展示训练误差和测试误差随迭代次数的变化，以评估模型的收敛情况。

• • 预测结果与实际结果的比较图：展示测试集上的实际值和预测值的散点图，以评估模型的预测效果。

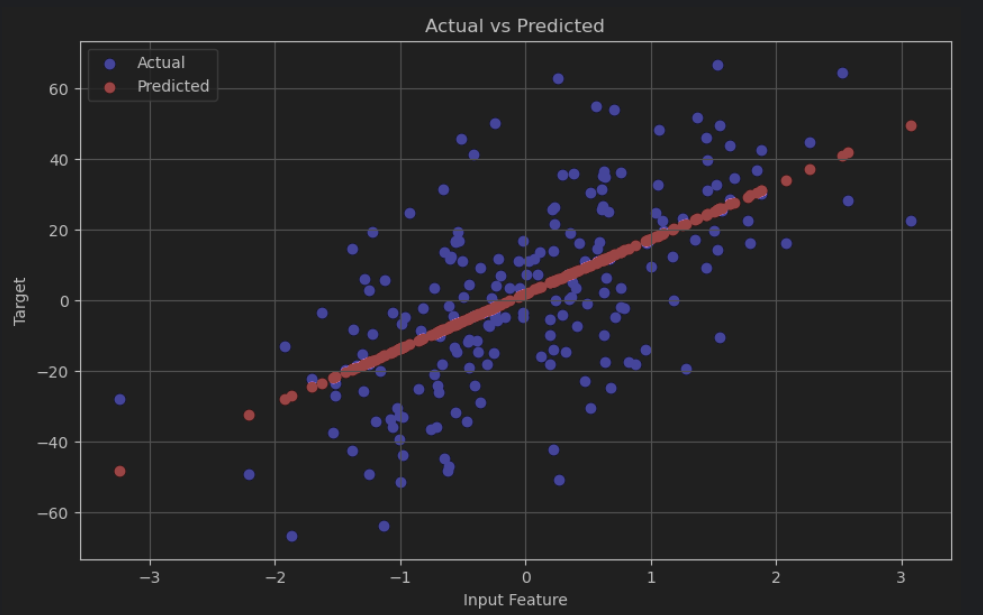
• • 参数更新的轨迹图：展示模型系数在每个 epoch 的更新情况，以了解参数的收敛过程。

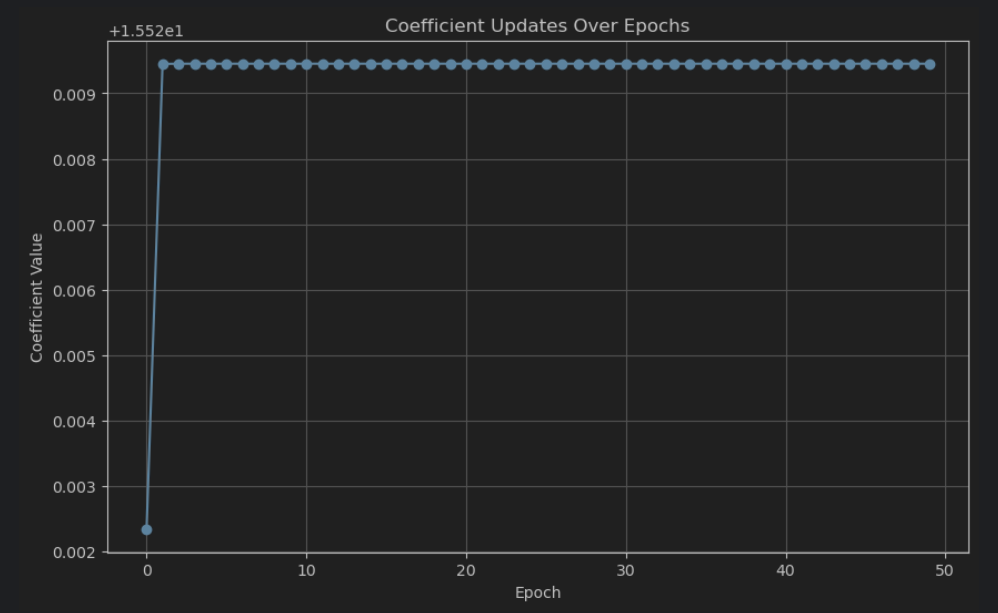
通过以上步骤，我们可以全面了解随机梯度下降算法在回归问题中的应用，以及模型训练过程中的各项指标变化情况。

结论

在这个案例中，我们生成了一个带有噪声的线性回归数据集，并使用随机梯度下降（SGD）进行模型训练。通过分析损失函数的收敛图、预测结果与实际结果的比较图，以及参数更新的轨迹图，我们可以清楚地了解模型的训练过程和效果。SGD 由于在每次迭代中使用了不同的样本，使得参数更新更加频繁，有助于更快地逼近目标函数的最小值。

案例：用随机梯度下降法预测员工工资

案例描述

假设你是一位外企人力资源分析师，希望根据员工的工作经验（年）和学历水平（学位）来预测他们的工资。你可以使用随机梯度下降法（SGD）来进行线性回归分析，以构建一个工资预测模型。

场景细节

• 目标：根据员工的工作经验和学历水平预测工资。
• 数据集：我们将生成一个模拟的数据集，包括1000个样本，每个样本包含工作经验（年）、学历水平（学位，使用1-3表示高中、学士、硕士）和工资（美元）。数据集带有一定的噪声，以模拟真实数据中的误差。
• 步骤：

1. 1. 生成数据集。
   2. 划分数据集为训练集和测试集。
   3. 初始化随机梯度下降法回归模型。
   4. 训练模型并记录训练误差和测试误差。
   5. 可视化结果，包括损失函数的收敛图、预测结果与实际结果的比较图、以及参数更新的轨迹图。

代码实现

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
from sklearn.model_selection import train_test_split
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler# 设置默认字体
rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体
rcParams['axes.unicode_minus'] = False  # 解决负号显示问题# 生成模拟员工工资数据
np.random.seed(42)
n_samples = 1000
X_experience = np.random.rand(n_samples, 1) * 40  # 工作经验在0到40年之间
X_education = np.random.randint(1, 4, size=(n_samples, 1))  # 学历水平：1-高中，2-学士，3-硕士
X = np.hstack([X_experience, X_education])
y = 20000 + 3000 * X_experience + 10000 * X_education + np.random.randn(n_samples, 1) * 5000  # 工资公式，带有噪声# 检查生成的数据
print("前5条数据和对应的目标值：")
print(X[:5])
print(y[:5])# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 标准化数据
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)# 初始化SGD回归模型
sgd = SGDRegressor(max_iter=1, tol=None, warm_start=True, learning_rate='constant', eta0=0.01, random_state=42)# 记录训练过程中的信息
n_epochs = 50
train_errors, test_errors = [], []
coef_updates = []# 训练模型
for epoch in range(n_epochs):sgd.fit(X_train_scaled, y_train.ravel())y_train_predict = sgd.predict(X_train_scaled)y_test_predict = sgd.predict(X_test_scaled)train_errors.append(mean_squared_error(y_train, y_train_predict))test_errors.append(mean_squared_error(y_test, y_test_predict))coef_updates.append(sgd.coef_.copy())# 检查预测值范围
print("预测值的最大值：", np.max(y_test_predict))
print("预测值的最小值：", np.min(y_test_predict))# 绘制损失函数的收敛图
plt.figure(figsize=(12, 8))
plt.plot(train_errors, label='训练误差')
plt.plot(test_errors, label='测试误差')
plt.xlabel('迭代次数')
plt.ylabel('均方误差')
plt.title('训练和测试误差随迭代次数的变化')
plt.legend()
plt.grid()
plt.show()# 绘制预测结果与实际结果的比较图
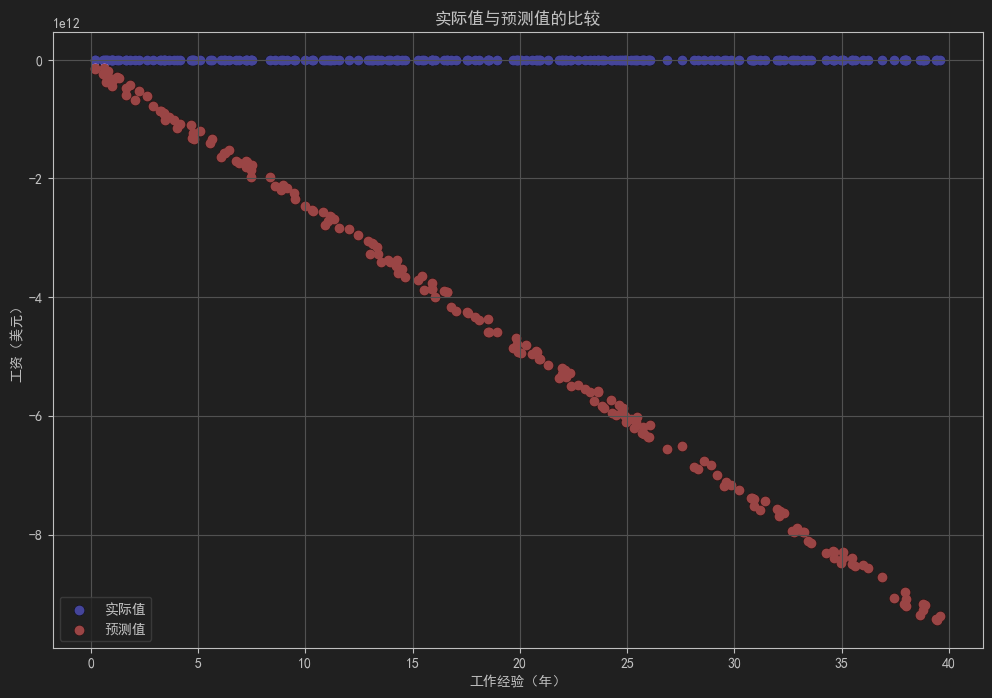
plt.figure(figsize=(12, 8))
plt.scatter(X_test[:, 0], y_test, color='blue', label='实际值')
plt.scatter(X_test[:, 0], y_test_predict, color='red', label='预测值')
plt.xlabel('工作经验（年）')
plt.ylabel('工资（美元）')
plt.title('实际值与预测值的比较')
plt.legend()
plt.grid()
plt.show()# 绘制参数更新的轨迹图
coef_updates = np.array(coef_updates)
plt.figure(figsize=(12, 8))
for i in range(coef_updates.shape[1]):plt.plot(coef_updates[:, i], marker='o', label=f'系数 {i}')
plt.xlabel('迭代次数')
plt.ylabel('系数值')
plt.title('系数更新轨迹')
plt.legend()
plt.grid()
plt.show()

加入了标准化步骤，并包含所有检查点以确保数据的范围和模型的训练效果正确。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
from sklearn.model_selection import train_test_split
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler# 设置默认字体
rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体
rcParams['axes.unicode_minus'] = False  # 解决负号显示问题# 生成模拟员工工资数据
np.random.seed(42)
n_samples = 1000
X_experience = np.random.rand(n_samples, 1) * 40  # 工作经验在0到40年之间
X_education = np.random.randint(1, 4, size=(n_samples, 1))  # 学历水平：1-高中，2-学士，3-硕士
X = np.hstack([X_experience, X_education])
y = 20000 + 3000 * X_experience + 10000 * X_education + np.random.randn(n_samples, 1) * 5000  # 工资公式，带有噪声# 检查生成的数据
print("前5条数据和对应的目标值：")
print(X[:5])
print(y[:5])# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 标准化数据
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)# 初始化SGD回归模型
sgd = SGDRegressor(max_iter=1, tol=None, warm_start=True, learning_rate='constant', eta0=0.01, random_state=42)# 记录训练过程中的信息
n_epochs = 50
train_errors, test_errors = [], []
coef_updates = []# 训练模型
for epoch in range(n_epochs):sgd.fit(X_train_scaled, y_train.ravel())y_train_predict = sgd.predict(X_train_scaled)y_test_predict = sgd.predict(X_test_scaled)train_errors.append(mean_squared_error(y_train, y_train_predict))test_errors.append(mean_squared_error(y_test, y_test_predict))coef_updates.append(sgd.coef_.copy())# 检查预测值范围
print("预测值的最大值：", np.max(y_test_predict))
print("预测值的最小值：", np.min(y_test_predict))# 绘制损失函数的收敛图
plt.figure(figsize=(12, 8))
plt.plot(train_errors, label='训练误差')
plt.plot(test_errors, label='测试误差')
plt.xlabel('迭代次数')
plt.ylabel('均方误差')
plt.title('训练和测试误差随迭代次数的变化')
plt.legend()
plt.grid()
plt.show()# 绘制预测结果与实际结果的比较图
plt.figure(figsize=(12, 8))
plt.scatter(X_test[:, 0], y_test, color='blue', label='实际值')
plt.scatter(X_test[:, 0], y_test_predict, color='red', label='预测值')
plt.xlabel('工作经验（年）')
plt.ylabel('工资（美元）')
plt.title('实际值与预测值的比较')
plt.legend()
plt.grid()
plt.show()# 绘制参数更新的轨迹图
coef_updates = np.array(coef_updates)
plt.figure(figsize=(12, 8))
for i in range(coef_updates.shape[1]):plt.plot(coef_updates[:, i], marker='o', label=f'系数 {i}')
plt.xlabel('迭代次数')
plt.ylabel('系数值')
plt.title('系数更新轨迹')
plt.legend()
plt.grid()
plt.show()

这个代码片段包括了数据生成、标准化、模型训练和可视化步骤。通过标准化数据，我们可以帮助模型更好地收敛，并避免由于数据范围问题导致的异常结果。

详细步骤解释

1. 生成数据：

• • 使用 numpy 生成一个包含工作经验（0-40年）和学历水平（高中、学士、硕士）的模拟数据集。
  • 使用工资公式生成目标值，公式中包括常数项、工作经验和学历水平的系数，以及一定的随机噪声。

1. 划分数据集：

• • 使用 train_test_split 将数据集划分为训练集（80%）和测试集（20%）。

1. 初始化模型：

• • 使用 SGDRegressor 初始化随机梯度下降回归模型，设置 max_iter=1 和 warm_start=True 以确保每次迭代都使用上次的解。
  • 设置常数学习率（learning_rate='constant'）和初始学习率（eta0=0.01）。

1. 模型训练：

• • 进行 50 次迭代（epochs），在每次迭代中使用训练数据训练模型。
  • 记录每次迭代的训练误差和测试误差，以及模型系数。

1. 结果可视化：

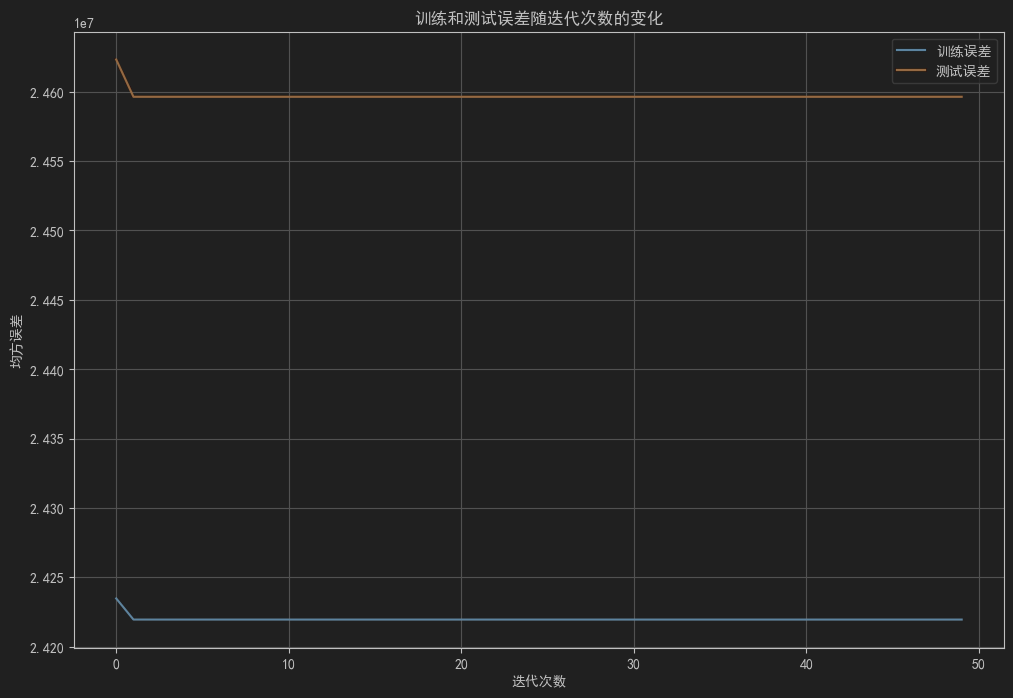
• • 损失函数的收敛图：展示训练误差和测试误差随迭代次数的变化。

标准化：

• • 预测结果与实际结果的比较图：展示测试集上的实际值和预测值的散点图。

标准化:

• • 参数更新的轨迹图：展示模型系数在每个 epoch 的更新情况。

标准化:

结论

通过以上步骤，我们构建了一个随机梯度下降法的回归模型，用于预测员工的工资。通过分析损失函数的收敛图、预测结果与实际结果的比较图，以及参数更新的轨迹图，我们可以清楚地了解模型的训练过程和效果。随机梯度下降法能够更快地更新参数，并且可以更容易地跳出局部最优解，从而更快地逼近目标函数的最小值。