c++ 高精度加法(只支持正整数)
再给大家带来一篇高精度,不过这次是高精度加法!话不多说,开整!
声明
与之前那篇文章一样,如果看起来费劲可以结合总代码来看
定义
由于加法进位最多进1位,所以我们的结果ans[]的长度定义为两个加数中最长长度+1即可
所有变量声明、输入环节和初始化:
string j1,j2;//两个加数
int l1=j1.length(),l2=j2.length();//两个加数的长度,确保只调用一次length()函数,节约时间
int ans[max(l1,l2)+1],step=max(l1,l2);//ans[]为最终结果,step可以理解为ans的下标
int t1,t2,jinWei=0,weiShu;//t1为j1中的一个数字,t2为j2中的一个数字
cout<<"加数1:";//输入
cin>>j1;
cout<<"加数2:";
cin>>j2;
for(int i=0;i<max(l1,l2);i++)ans[i]=0;计算过程(思路)
本文以123456+127来举例,计算过程如下:

我们可以发现从j1[4]+j2[2] 开始,最后得到ans[4]=2;
也就是从两个加数的最后一位开始加,加的结果的个位与上一位的进位的和存入ans[]的最后一位中,然后推进到下一位,以此类推
计算过程(实现)
由思路可以得出以下for循环:由于有j1的长度更长 、j2的长度更长和两个加数的长度相等三种情况,所以要分情况取本轮加数(-‘0’为char转int,详见c/c++ char和int互转)
for(int i=min(l1,l2)-1;i>=0;i--){if(l1>l2){//j1的长度更长t1=j1[i+(l1-l2)]-'0';//由于两个加数的长度有偏差,所以数组的下标也不相同(如j1[4]应与j2[2]相加),两个下标之差便是两个加数的长度之差t2=j2[i]-'0';}else if(l1<l2){//j2的长度更长 t1=j1[i]-'0';t2=j2[i+(l2-l1)]-'0';}else{//两个加数的长度相等 t1=j1[i]-'0';t2=j2[i]-'0';}ans[step--]=(t1+t2+jinWei)%10;//step--是因为ans中已经存入了一位数,(t1+t2+jinWei)%10即两数的第i位与上一步的进位相加的和的个位jinWei=(t1+t2+jinWei)/10;
}以上的代码结束于示例中j1[2]+j1[0]存入ans[3]并保留jinWei=0的操作,此时还有j1[0]和j1[1]没有操作,对于这两位,仅仅需要从j1[1]开始倒退,用j1[1]加上一步的jinWei并存入ans[]中,刷新jinWei即可,如下,初始值为长度差-1(因为两个加数中长度更短的数已经加完了,没有操作的便是较长数剩下的部分,由于下标从0开始,就要-1) :这里又存在j1的长度更长 、j2的长度更长两种情况,所以要分情况取本轮加数,与上个for相似
for(int i=max(l1,l2)-min(l1,l2)-1;i>=0;i--){ if(l1>l2){//j1的长度更长 t1=j1[i]-'0';ans[step--]=(t1+jinWei)%10;//与上个for相似的操作 jinWei=(t1+jinWei)/10;}else if(l1<l2){//j2的长度更长t2=j2[i]-'0';ans[step--]=(t2+jinWei)%10;jinWei=(t2+jinWei)/10;}
}ok,在运行完上面这段代码后,所有的位都处理完了,但是最后一轮的jinWei还没有处理,所以让ans[step]+=jinWei(也可以用ans[0]=jinWei,都是一样的)就处理完了整个计算过程:
ans[step]+=jinWei;打印
因为计算后可能会出现最后一轮没有进位,就像上面举得那个例子一样,那么ans[0]就会是0,这种首位是0的情况当然是不打印为好,如此一来我们就要计算结果的位数(开头定义的weiShu):
//ans[]的最大位数为max(l1,l2)+1,没有进位(jinWei==0)时位数就为最大位数-1(因为首位为0),否则就是有进位,此时的位数为最大位数
if(jinWei==0)weiShu=max(l1,l2);
else weiShu=max(l1,l2)+1;最后用一个for打印出来:起始值为最大位数减去weiShu,以此来确定起始值为0还是1
cout<<"和:";
for(int i=max(l1,l2)+1-weiShu;i<max(l1,l2)+1;i++)cout<<ans[i];
cout<<endl;总代码
激动人心的时刻,准备好了吗?
#include<iostream>
using namespace std;
int main(){string j1,j2;//两个加数 int l1=j1.length(),l2=j2.length();//两个加数的长度,确保只调用一次length()函数,节约时间 int ans[max(l1,l2)+1],step=max(l1,l2);//ans[]为最终结果,step可以理解为ans的下标 int t1,t2,jinWei=0,weiShu;//t1为j1中的一个数字,t2为j2中的一个数字 cout<<"加数1:";//输入 cin>>j1;cout<<"加数2:";cin>>j2;for(int i=0;i<max(l1,l2);i++)ans[i]=0;for(int i=min(l1,l2)-1;i>=0;i--){if(l1>l2){//j1的长度更长 t1=j1[i+(l1-l2)]-'0';//由于两个加数的长度有偏差,所以数组的下标也不相同(如j1[4]应与j2[2]相加),两个下标之差便是两个加数的长度之差 t2=j2[i]-'0';}else if(l1<l2){//j2的长度更长 t1=j1[i]-'0';t2=j2[i+(l2-l1)]-'0';}else{//两个加数的长度相等 t1=j1[i]-'0';t2=j2[i]-'0';}ans[step--]=(t1+t2+jinWei)%10;//step--是因为ans中已经存入了一位数,(t1+t2+jinWei)%10即两数的第i位与上一步的进位相加的和的个位 jinWei=(t1+t2+jinWei)/10;}for(int i=max(l1,l2)-min(l1,l2)-1;i>=0;i--){ if(l1>l2){//j1的长度更长 t1=j1[i]-'0';ans[step--]=(t1+jinWei)%10;//与上个for相似的操作 jinWei=(t1+jinWei)/10;}else if(l1<l2){//j2的长度更长t2=j2[i]-'0';ans[step--]=(t2+jinWei)%10;jinWei=(t2+jinWei)/10;}}ans[step]+=jinWei;//ans[]的最大位数为max(l1,l2)+1,没有进位(jinWei==0)时位数就为最大位数-1(因为首位为0),否则就是有进位,此时的位数为最大位数if(jinWei==0)weiShu=max(l1,l2);else weiShu=max(l1,l2)+1;cout<<"和:";for(int i=max(l1,l2)+1-weiShu;i<max(l1,l2)+1;i++)cout<<ans[i];cout<<endl;
}如有疑问或有办法将此代码变为支持所有数欢迎评论区留言或私信(支持所有数的我会尽快做好)
相关文章:

c++ 高精度加法(只支持正整数)
再给大家带来一篇高精度,不过这次是高精度加法!话不多说,开整! 声明 与之前那篇文章一样,如果看起来费劲可以结合总代码来看 定义 由于加法进位最多进1位,所以我们的结果ans[]的长度定义为两个加数中最…...

python键盘操作工具:ctypes、pyautogui
这里模拟 Win Ctrl L 组合键 1、ctypes ctypes库,它允许我们直接调用Windows API来模拟键盘输入。 import ctypes import time# 定义所需的常量和结构 LONG ctypes.c_long DWORD ctypes.c_ulong ULONG_PTR ctypes.POINTER(DWORD) WORD ctypes.c_ushortclass…...

计算机网络发展历史
定义和基本概念 计算机网络是由多个计算设备通过通信线路连接起来的集合,这些设备能够互相交换数据、消息和资源。计算机网络的核心功能是实现数据的远程传输和资源共享,它使得地理位置的限制被大大减弱,极大地促进了信息的自由流动和人类社…...

记录安装android studio踩的坑 win7系统
最近在一台新电脑上安装android studio,报了很多错误,也是费了大劲才解决,发出来大家一起避免一些问题,找到解决方法。 安装时一定要先安装jdk,cmd命令行用java -version查当前的版本,没有的话,先安装jdk,g…...

Python图形编程-PyGame快速入门
PyGame快速入门 文章目录 PyGame快速入门1、什么是PyGame2、安装PyGame3、创建PyGame窗口4、处理事件5、绘制对象6、移动对象7、加载和显示图像8、播放声音9、处理用户输入10、碰撞检测11、动画精灵12、管理游戏状态13、Pygame 中的典型主游戏循环1、什么是PyGame Pygame 是一…...

邦芒宝典:8种方法调整职场心态
在职场中拼斗当然要有好的心态,您知道职场心态如何调整吗? 方法1:自我调整 “思想可以使天堂变成地狱,也可以使地狱变成天堂。”你不能样样顺利,但可以事事尽心;你不能左右天气,但可以改变心情;你…...

华为OD2024D卷机试题汇总,含D量50%+,按算法分类刷题,事半功倍
目录 专栏导读华为OD机试算法题太多了,知识点繁杂,如何刷题更有效率呢? 一、逻辑分析二、数据结构1、线性表① 数组② 双指针 2、map与list3、队列4、链表5、栈6、滑动窗口7、二叉树8、并查集9、矩阵 三、算法1、基础算法① 贪心思维② 二分查…...

Unity UGUI 之 Graphic Raycaster
本文仅作学习笔记与交流,不作任何商业用途 本文包括但不限于unity官方手册,唐老狮,麦扣教程知识,引用会标记,如有不足还请斧正 首先手册连接如下: Unity - Manual: Graphic Raycaster 笔记来源于ÿ…...

类和对象——相关的零碎知识
前提提示: 其实C中的类和对象,最重要的是6个默认函数,如有忘记,请移步到:类和对象。本章是对于一些细节知识的补充和拓展。 1. 隐示类型转换 在运算时,运算符左右两边的操作数的类型不同,编译器…...

【hadoop大数据集群 1】
hadoop大数据集群 1 文章目录 hadoop大数据集群 1一、环境配置1.安装虚拟机2.换源3.安装工具4.安装JDK5.安装Hadoop 一、环境配置 折腾了一下午/(ㄒoㄒ)/~~ 1.安装虚拟机 参考视频:https://www.bilibili.com/video/BV18y4y1G7JA?p17&vd_sourcee15e83ac6b22a…...

TQSDRPI开发板教程:实现PL端的UDP回环与GPSDO
本教程将完成一个全面的UDP运行流程与GPSDO测试,从下载项目的源代码开始,通过编译过程,最终将项目部署到目标板卡上运行演示。此外,我们还介绍如何修改板卡的IP地址,以便更好地适应您的网络环境或项目需求。 首先从Gi…...
 ==> 查找数组list中,是否有包含与当前currKey的值不一样的misId)
array.some() ==> 查找数组list中,是否有包含与当前currKey的值不一样的misId
需求: const list [ {misId: e, name: 小白}, {misId: e, name: 小白白}, {misId: r, name: 小王}, {misId: r, name: 小小王} ] let currKey r 查找数组list中,是否有包含与当前currKey的值不一样的misId 解决: 要查找数组lis…...
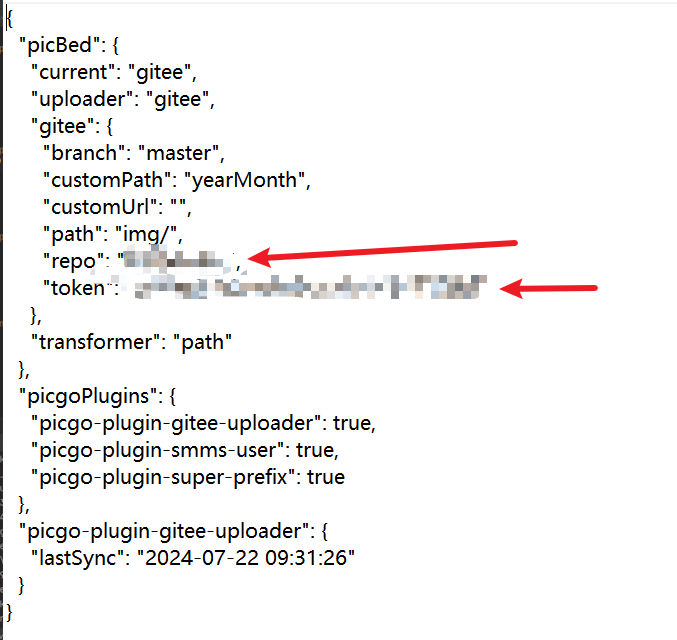
最简单的typora+gitee+picgo配置图床
typoragiteepicgo图床 你是否因为管理图片而感到头大?是时候了解一下 Typora、Gitee 和 PicGo 这个超级三剑客了,它们可以帮你轻松打造自己的图床,让你的博客图片管理变得简单又有趣。让我们开始这场神奇的图床之旅吧! Typora …...

【黄啊码】GPT的相关名词解释
GPT是一种基于互联网的、可用数据来训练的、文本生成的深度学习模型 GPT的核心技术是变换器(Transformer),这是一种神经网络结构,可以有效地处理序列数据,比如文本、语音、图像等。GPT使用了大量的预训练数据&#…...

git stash 命令详解
git stash 描述 git stash 命令用于将当前工作目录中的未提交更改(包括暂存区和工作区的更改)保存到一个栈中,并恢复工作目录到干净的 HEAD 状态。这样您可以在不提交当前更改的情况下,切换到其他分支或进行其他操作。后续可以通…...

txt格式单词导入有道词典生词本 (java代码方式)
txt格式单词导入有道词典生词本 (java代码方式) 首先要求txt文档里单词的格式,大概需要像这种: 每行是一个单词,格式为:英文单词空格词性单词意思。 注意 导出单词本的名字就是你 txt 文件的名字 我这里是 公共英语三级 单词本 …...

轨迹优化 | 基于ESDF的共轭梯度优化算法(附ROS C++/Python仿真)
目录 0 专栏介绍1 数值优化:共轭梯度法2 基于共轭梯度法的轨迹优化2.1 障碍约束函数2.2 曲率约束函数2.3 平滑约束函数 3 算法仿真3.1 ROS C实现3.2 Python实现 0 专栏介绍 🔥课程设计、毕业设计、创新竞赛、学术研究必备!本专栏涉及更高阶的…...
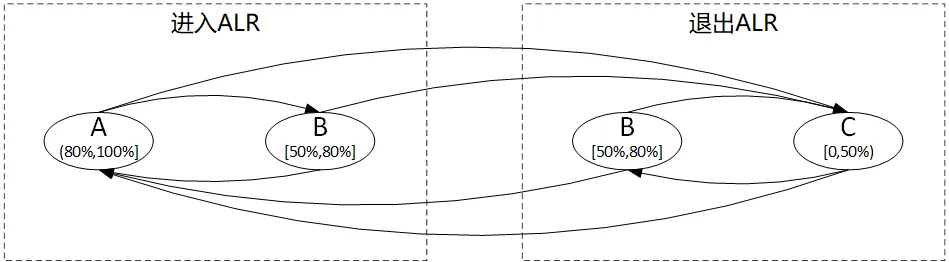
深入浅出WebRTC—ALR
ALR(Application Limited Region)指的是网络传输过程中,由于应用层的限制(而非网络拥塞)导致带宽未被充分利用的情况。在这种情况下,应用层可能因为处理能力、手动配置或其他因素无法充分利用可用带宽&…...

BSV区块链技术现实应用原理解析
BSV区块链以其卓越的可扩展性、坚如磐石的安全性、极低的交易成本等特性,成为满足企业当下需求并为企业未来成功奠基铺路的理想技术。 BSV协会近期发布了一个题为《驾驭数字化转型:在自动化世界中建立信任——区块链在数据保护和交易优化中的角色》的报…...

七大基于比较的排序算法
目录 一、基于比较的排序算法概述 1. 插入排序(Insertion Sort) 2. 选择排序(Selection Sort) 3. 冒泡排序(Bubble Sort) 4. 归并排序(Merge Sort) 5. 快速排序(Qu…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...
