七大基于比较的排序算法
目录
一、基于比较的排序算法概述
1. 插入排序(Insertion Sort)
2. 选择排序(Selection Sort)
3. 冒泡排序(Bubble Sort)
4. 归并排序(Merge Sort)
5. 快速排序(Quick Sort)
6. 堆排序(Heap Sort)
7. 希尔排序(Shell Sort)
二、排序算法的性能分析
三、Java中的常用排序方法
在计算机科学中,排序算法是处理数据结构的核心算法之一。它不仅直接影响程序的性能,还影响到数据的传输和存储效率。本文将深入探讨七种基于比较的排序算法,包括它们的基本原理、实现方法和性能分析,同时也会介绍Java中常用的排序方法。
一、基于比较的排序算法概述
基于比较的排序算法是指通过比较元素之间的大小关系来确定元素的排列顺序的算法。这类算法的时间复杂度下界为O(n log n)。根据不同的策略和实现,常见的基于比较的排序算法包括插入排序、选择排序、冒泡排序、归并排序、快速排序、堆排序以及希尔排序。以下对这七种排序算法进行详细介绍。
1. 插入排序(Insertion Sort)
原理
插入排序是一种简单且直观的排序算法。它通过构建一个有序的序列,将待排序的元素逐步插入到已排序序列中,直到所有元素都在正确的位置。
实现
public static void insertionSort(int[] array) { for (int i = 1; i < array.length; i++) { int key = array[i]; int j = i - 1; while (j >= 0 && array[j] > key) { array[j + 1] = array[j]; j--; } array[j + 1] = key; }
} 性能分析
插入排序的时间复杂度为O(n²),适合小规模数据的排序。其空间复杂度为O(1),是一个原地排序算法。对几乎已经排序的数据集,其性能接近O(n)。
2. 选择排序(Selection Sort)
原理
选择排序通过反复选择未排序部分的最小元素,逐步将其放到已排序部分的末尾。
实现
public static void selectionSort(int[] array) { for (int i = 0; i < array.length - 1; i++) { int minIndex = i; for (int j = i + 1; j < array.length; j++) { if (array[j] < array[minIndex]) { minIndex = j; } } int temp = array[minIndex]; array[minIndex] = array[i]; array[i] = temp; }
} 性能分析
选择排序的时间复杂度为O(n²),空间复杂度为O(1)。它不适合大规模数据排序,因为在最坏情况下仍然需要n²的比较次数。
3. 冒泡排序(Bubble Sort)
原理
冒泡排序通过重复遍历待排序的元素,比较相邻元素并根据大小关系进行交换,直到没有元素需要交换为止。
实现
public static void bubbleSort(int[] array) { int n = array.length; for (int i = 0; i < n - 1; i++) { for (int j = 0; j < n - 1 - i; j++) { if (array[j] > array[j + 1]) { int temp = array[j]; array[j] = array[j + 1]; array[j + 1] = temp; } } }
} 性能分析
冒泡排序的时间复杂度为O(n²),空间复杂度为O(1)。尽管实现简单,但由于其性能性能较差,通常不用于实际应用。
4. 归并排序(Merge Sort)
原理
归并排序采用分治法,将待排序数组分成两个子数组,分别对其进行排序后再合并成一个有序数组。实现
public static void mergeSort(int[] array) { if (array.length < 2) { return; } int mid = array.length / 2; int[] left = Arrays.copyOfRange(array, 0, mid); int[] right = Arrays.copyOfRange(array, mid, array.length); mergeSort(left); mergeSort(right); merge(array, left, right);
} private static void merge(int[] array, int[] left, int[] right) { int i = 0, j = 0, k = 0; while (i < left.length && j < right.length) { if (left[i] <= right[j]) { array[k++] = left[i++]; } else { array[k++] = right[j++]; } } while (i < left.length) { array[k++] = left[i++]; } while (j < right.length) { array[k++] = right[j++]; }
} 性能分析
归并排序的时间复杂度为O(n log n),空间复杂度为O(n)。由于其稳定性和较优的性能,常用于大规模数据排序。
5. 快速排序(Quick Sort)
原理
快速排序也采用分治法,通过选择一个“基准”元素,将数组分成小于和大于基准的两个部分,递归地对这两个部分进行排序。实现
public static void quickSort(int[] array, int low, int high) { if (low < high) { int pivotIndex = partition(array, low, high); quickSort(array, low, pivotIndex - 1); quickSort(array, pivotIndex + 1, high); }
} private static int partition(int[] array, int low, int high) { int pivot = array[high]; int i = low - 1; for (int j = low; j < high; j++) { if (array[j] < pivot) { i++; int temp = array[i]; array[i] = array[j]; array[j] = temp; } } int temp = array[i + 1]; array[i + 1] = array[high]; array[high] = temp; return i + 1;
} 性能分析
快速排序的平均时间复杂度为O(n log n),最坏情况为O(n²)(如已经有序数组),空间复杂度为O(log n)。快速排序在大多数情况下表现优秀,尤其适用于大规模数据排序。
6. 堆排序(Heap Sort)
原理
堆排序利用堆结构 以确定元素的顺序。首先构建一个最大堆,将堆顶元素与最后一个元素交换,缩小堆并调整已构建的堆。实现
public static void heapSort(int[] array) { int n = array.length; for (int i = n / 2 - 1; i >= 0; i--) { heapify(array, n, i); } for (int i = n - 1; i >= 0; i--) { int temp = array[0]; array[0] = array[i]; array[i] = temp; heapify(array, i, 0); }
} private static void heapify(int[] array, int n, int i) { int largest = i; int left = 2 * i + 1; int right = 2 * i + 2; if (left < n && array[left] > array[largest]) { largest = left; } if (right < n && array[right] > array[largest]) { largest = right; } if (largest != i) { int swap = array[i]; array[i] = array[largest]; array[largest] = swap; heapify(array, n, largest); }
} 性能分析
堆排序的时间复杂度为O(n log n),空间复杂度为O(1)。由于其不稳定性,使用场景受到一定限制。
7. 希尔排序(Shell Sort)
原理
希尔排序是插入排序的一种改进版,通过使用间隔进行分组,实现对每组内的元素进行插入排序,从而最终达到整体有序。
实现
public static void shellSort(int[] array) { int n = array.length; for (int gap = n / 2; gap > 0; gap /= 2) { for (int i = gap; i < n; i++) { int temp = array[i]; int j; for (j = i; j >= gap && array[j - gap] > temp; j -= gap) { array[j] = array[j - gap]; } array[j] = temp; } }
} 性能分析
希尔排序的时间复杂度取决于间隔序列的选择,通常在O(n log n)与O(n²)之间。具有不稳定性,适用于中等规模的数据排序。
二、排序算法的性能分析
排序算法的性能分析主要从时间复杂度和空间复杂度两个方面进行。
时间复杂度:描述算法执行所需时间与输入规模之间的关系。大多数已知的排序算法都具有O(n²)和O(n log n)的时间复杂度,差别主要体现在算法的实际常数因子以及适用的输入规模和分布特征。
空间复杂度:描述算法执行所需额外存储空间与输入规模之间的关系。原地排序算法(如堆排序、快速排序)在空间复杂度方面表现优异,而归并排序等需要额外存储空间的算法则性能较差,适用于内存充足的情况。
三、Java中的常用排序方法
在Java中,除了自定义实现的排序算法外,Java Collections框架也提供了多种高效的排序方法。例如,Arrays.sort()和Collections.sort()分别用于数组和集合的排序。这些排序方法通常使用的是优化后的快速排序算法,性能优越且易于使用。
Arrays.sort(array); // 数组排序
Collections.sort(list); // 集合排序
此外,在Java 8及其之后的版本中引入了并行流(parallel streams),以支持并行排序,通过更好地利用多核处理器资源来提高排序性能。
相关文章:

七大基于比较的排序算法
目录 一、基于比较的排序算法概述 1. 插入排序(Insertion Sort) 2. 选择排序(Selection Sort) 3. 冒泡排序(Bubble Sort) 4. 归并排序(Merge Sort) 5. 快速排序(Qu…...
)
web前端 React 框架面试200题(四)
面试题 97. React 两种路由模式的区别?hash和history? 参考回答: 1: hash路由 hash模式是通过改变锚点(#)来更新页面URL,并不会触发页面重新加载,我们可以通过window.onhashchange监听到hash的改变,从而处…...
5.Fabric的共识机制
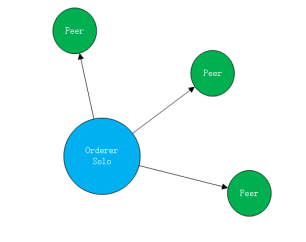
在Fabric中,有以下3中典型共识机制。 Solo共识 solo共识机制只能用于单节点模式,即只能有一个Orderer节点,因此,其共识过程很简单,每接收到一个交易信息,就在共识模块的控制下产生区块并广播给节点存储到账本中。 Solo 模式下的共识只适用于一个Orderer节点,所以可以在…...

【safari】react在safari浏览器中,遇到异步时间差的问题,导致状态没有及时更新到state,引起传参错误。如何解决
在safari浏览器中,可能会遇到异步时间差的问题,导致状态没有及时更新到state,引起传参错误。 PS:由于useState是一个普通的函数, 定义为() > void;因此此处不能用await/async替代setTimeout,只能用在返…...

京准:GPS北斗卫星授时信号安全隔离防护装置
京准:GPS北斗卫星授时信号安全隔离防护装置 京准:GPS北斗卫星授时信号安全隔离防护装置 1、主要特点 ★信号加固功能: GPS/BDS单系统信号拒止情况下(包含受到GPS L1欺骗干扰、GPS L1压制干扰、BDS B1欺骗干扰、BDS B1压制干扰&…...

解决方案架构师系列 - AWS - Pinpoint
AWS Pinpoint介绍 Amazon Pinpoint 为营销人员和开发人员提供了一款可自定义的工具,助力他们大规模地开展跨渠道、行业和活动的客户通信。 Amazon Pinpoint是一个全面的客户参与平台,旨在帮助营销人员和开发人员大规模地开展跨渠道、行业和活动的客…...
MF173:将多个工作表转换成PDF文件
我给VBA的定义:VBA是个人小型自动化处理的有效工具。利用好了,可以大大提高自己的工作效率,而且可以提高数据的准确度。“VBA语言専攻”提供的教程一共九套,分为初级、中级、高级三大部分,教程是对VBA的系统讲解&#…...

Docker、containerd、CRI-O 和 runc 之间的区别
容器与 Docker 这个名称并不紧密相关。你可以使用其他工具来运行容器 您可以使用 Docker 或一堆非Docker 的其他工具来运行容器。docker只是众多选项之一,Docker(公司)在生态系统中创建了一些很棒的工具,但不是全部。 容器方面有…...

PRISM-Python 中的规则一个简单的 Python 规则感应系统
欢迎来到雲闪世界.PRISM 是一种现有算法(尽管我确实创建了一个 Python 实现),PRISM 相对简单,但在机器学习中,有时最复杂的解决方案效果最好,有时最简单的解决方案效果最好。然而,当我们希望建立…...

DB-GPT:LLM应用的集大成者
整体架构 架构解读 可以看到,DB-GPT把架构抽象为7层,自下而上分别为: 运行环境:支持本地/云端&单机/分布式等部署方式。顺便一提,RAY是蚂蚁深度参与的一个开源项目,所以对RAY功能的支持应该非常完善。…...
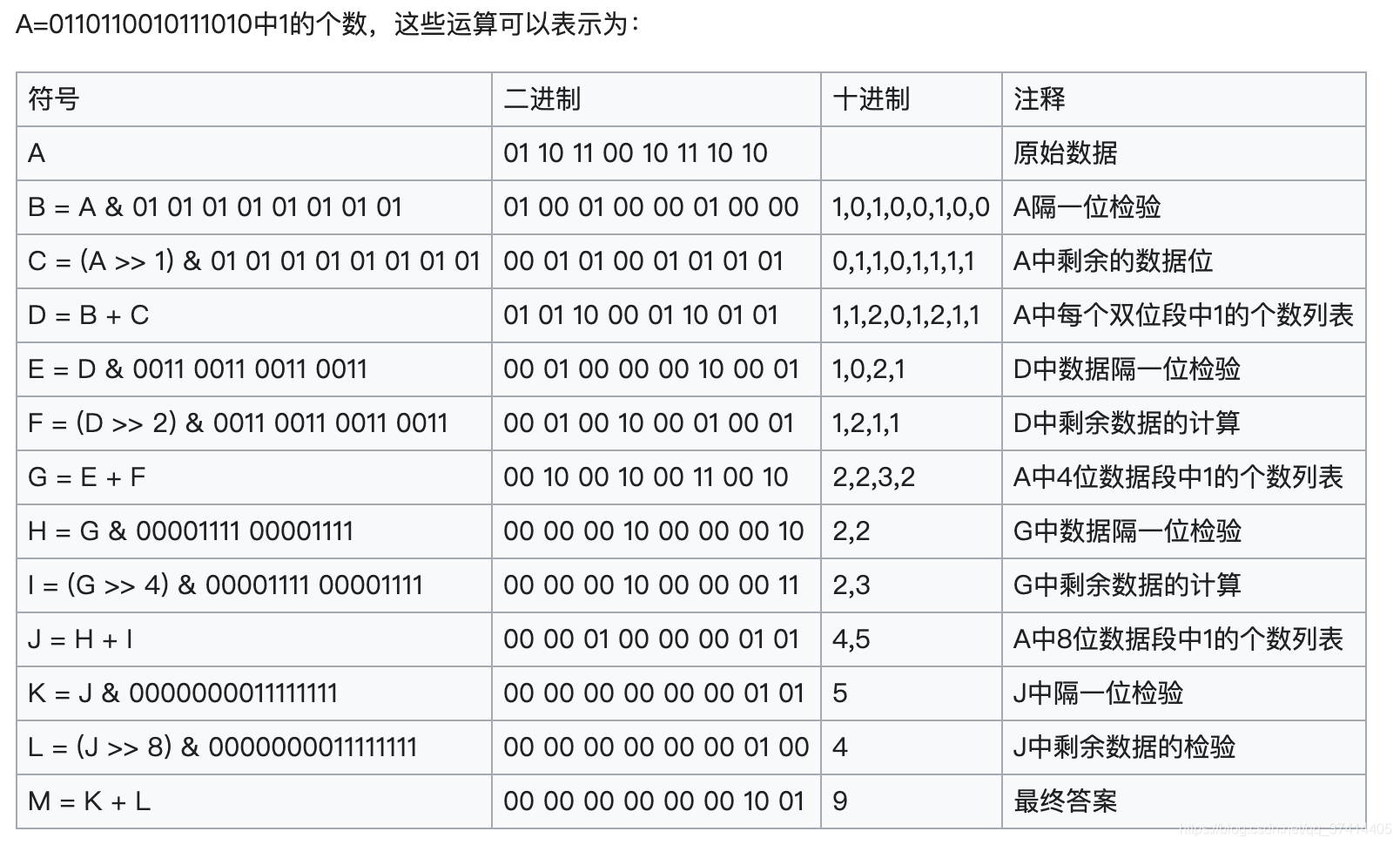
汉明权重(Hamming Weight)(统计数据中1的个数)VP-SWAR算法
汉明权重(Hamming Weight)(统计数据中1的个数)VP-SWAR算法 定义 汉明重量是一串符号中非零符号的个数。它等于同样长度的全零符号串的汉明距离(在信息论中,两个等长字符串之间的汉明距离等于两个字符串对应位置的不同…...

基于 PyTorch 的模型瘦身三部曲:量化、剪枝和蒸馏,让模型更短小精悍!
基于 PyTorch 的模型量化、剪枝和蒸馏 1. 模型量化1.1 原理介绍1.2 PyTorch 实现 2. 模型剪枝2.1 原理介绍2.2 PyTorch 实现 3. 模型蒸馏3.1 原理介绍3.2 PyTorch 实现 参考文献 1. 模型量化 1.1 原理介绍 模型量化是将模型参数从高精度(通常是 float32࿰…...

二、原型模式
文章目录 1 基本介绍2 实现方式深浅拷贝目标2.1 使用 Object 的 clone() 方法2.1.1 代码2.1.2 特性2.1.3 实现深拷贝 2.2 在 clone() 方法中使用序列化2.2.1 代码 2.2.2 特性 3 实现的要点4 Spring 中的原型模式5 原型模式的类图及角色5.1 类图5.1.1 不限制语言5.1.2 在 Java 中…...

【目标检测】Anaconda+PyTorch(GPU)+PyCharm(Yolo5)配置
前言 本文主要介绍在windows系统上的Anaconda、PyTorch、PyCharm、Yolov5关键步骤安装,为使用yolo所需的环境配置完善。同时也算是记录下我的配置流程,为以后用到的时候能笔记查阅。 Anaconda 软件安装 Anaconda官网:https://www.anaconda…...

Django实战项目之进销存数据分析报表——第二天:项目创建和 PyCharm 配置
在上一篇博客中,我们讨论了如何搭建一个全栈 Web 应用的开发环境,包括 Python 环境的创建、Django 和 MySQL 的安装以及前端技术栈的选择。现在,让我们继续深入,学习如何在 PyCharm 中创建一个新的 Django 项目并进行配置。 一…...

静态路由实验
1.实验拓扑图 二、实验要求 1.R6为ISP,接口IP地址均为公有地址,该设备只能配置IP地址,之后不能再对其进行任何配置; 2.R1-R5为局域网,私有IP地址192.168.1.0/24,请合理分配; 3.R1、R2、R4&…...

VSCode STM32嵌入式开发插件记录
要卸载之前搭建的VSCode嵌入式开发环境了,记录一下用的插件。 1.Cortex-Debug https://github.com/Marus/cortex-debug 2.Embedded IDE https://github.com/github0null/eide 3.Keil uVision Assistant https://github.com/jacksonjim/keil-assistant/ 4.RTO…...

linux cpu 占用超100% 分析。
感谢: https://www.cnblogs.com/wolfstark/p/16450131.html 总结: 查看进程中各个线程占用百分比 top -H -p <pid> 某线程100%了 说明 任务处理不过来 会卡 但是永远不可能超100% 系统监视器里面看到的是 所有线程占用的 总和会超100%。 所以最好的情况是&…...

自然学习法和科学学习法
一、自然学习法 自然学习法:什么事自然学习法,特意让kimi来回答了一下。所谓的自然学习法说的俗一点就是野路子学习方法。这种学习方法的特点是“慢”“没有系统性”,学完之后感觉都会了,但是又感觉什么都不会。 二、科学学习法 …...
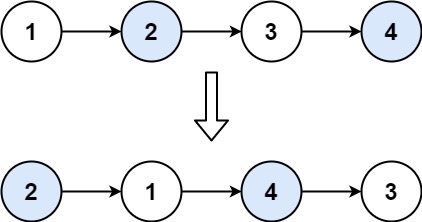
力扣第二十四题——两两交换链表中的节点
内容介绍 给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。 示例 1: 输入:head [1,2,3,4] 输出ÿ…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...
