静态路由实验
1.实验拓扑图

二、实验要求
1.R6为ISP,接口IP地址均为公有地址,该设备只能配置IP地址,之后不能再对其进行任何配置;
2.R1-R5为局域网,私有IP地址192.168.1.0/24,请合理分配;
3.R1、R2、R4,各有两个环回IP地址,R5,R6各有一个环回地址;所有路由器上环回均代表连接用户的接口;
4.R3下面的两台PC通过DHCP自动获取IP地址;
5.选路最佳,路由表尽量小,避免环路;
6.R1-R5均可以访问R6的环回;
7.在R1上配置telnet服务,使R6能通过R5的公有地址telnet到R1上;
8.R4与R5正常通过1000M链路,故障时通过100m链路;
三、实验思路
实验分析:
1 .R6为isp,接口IP地址均为公有有地址;该设备只能配置IP地址, 之后不能再对其进行任何配置(r6只能配置IP, 所以r1--r5上需要配置指向r6的缺省路由)
2 .R1—R5为局域网,私有P地址192.168.1.6/24,请合理分配;
图中骨干链路只需两个个IP,因此分配/30的网段即可,r1,r2,r4的俩个环回用大的网段划分成俩个小网段(减少黑洞路由的出现),然后按须分配。
3.R3下的两台PC通过DHCP自动获取IP地址(r3下启动DHCP服务)
4.选路最佳,路由表尽量小,避免环路;
(1)选路最佳需配置负载均衡,且经过的路由数目尽量少;
(2) 路由表尽量小则需进行汇总,与缺省路由通向的网段可省略;
(3)避免环路需进行空接口配置。
5.R1—R5均可以访问R6的环回;
因为R1-R5为内网,R6为公网,需在边界路由器R5上配置nat服务(EASYIP)
6. R6 telnet R5的公有IP地址时,实际登陆到R1上;
则R1上开启telnet服务,R5配置nat映射到R1的任意接口即可
7. R4与R5正常通过1000M链路,故障时通过100M链路;
因为R4与R5之间配置浮动静态路由,修改优先值。
实验配置:
[r1]interface GigabitEthernet 0/0/0
[r1-GigabitEthernet0/0/0]ip address 192.168.1.1 30
[r1-GigabitEthernet0/0/0]q
[r1]interface GigabitEthernet 0/0/1
[r1-GigabitEthernet0/0/1]ip address 192.168.1.9 30
[r1]interface LoopBack 0
[r1-LoopBack0]ip address 192.168.1.33 28
[r1-LoopBack0]q
[r1]interface LoopBack 1
[r1-LoopBack1]ip address 192.168.1.49 28[r2]interface GigabitEthernet 0/0/0
[r2-GigabitEthernet0/0/0]ip address 192.168.1.2 30
[r2-GigabitEthernet0/0/0]q
[r2]interface GigabitEthernet 0/0/1
[r2-GigabitEthernet0/0/1]ip address 192.168.1.5 30
[r2]interface LoopBack 0
[r2-LoopBack0]ip address 192.168.1.65 28
[r2-LoopBack0]q
[r2]interface LoopBack 1
[r2-LoopBack1]ip address 192.168.1.81 28[r3]interface GigabitEthernet 0/0/0
[r3-GigabitEthernet0/0/0]ip address 192.168.1.10 30
[r3-GigabitEthernet0/0/0]q
[r3]interface GigabitEthernet 0/0/1
[r3-GigabitEthernet0/0/1]ip address 192.168.1.13 30
[r3]interface GigabitEthernet 0/0/2
[r3-GigabitEthernet0/0/2]ip address 192.168.1.97 27[r4]interface GigabitEthernet 0/0/0
[r4-GigabitEthernet0/0/0]ip address 192.168.1.14 30
[r4-GigabitEthernet0/0/0]int gi 0/0/1
[r4-GigabitEthernet0/0/1]ip add 192.168.1.6 30
[r4-GigabitEthernet0/0/1]int gi 0/0/2
[r4-GigabitEthernet0/0/2]ip address 192.168.1.17 30
[r4-GigabitEthernet0/0/2]int gi 4/0/0
[r4-GigabitEthernet4/0/0]ip add 192.168.1.21 30
[r4]interface LoopBack 0
[r4-LoopBack0]IP address 192.168.1.129 28
[r4]interface LoopBack 1
[r4-LoopBack1]ip address 192.168.1.145 28[r5-GigabitEthernet0/0/0]ip address 192.168.1.22 30
[r5]interface GigabitEthernet 0/0/1
[r5-GigabitEthernet0/0/1]ip address 192.168.1.26 30
[r5]interface GigabitEthernet 0/0/2
[r5-GigabitEthernet0/0/2]ip address 192.168.1.29 30
[r5-GigabitEthernet0/0/2]ip address 56.1.1.1 24
[r5]interface LoopBack 0
[r5-LoopBack0]ip address 192.168.1.161 27[r6-GigabitEthernet0/0/0]ip address 56.1.1.2 24
[r6]interface LoopBack 0
[r6-LoopBack0]ip address 6.6.6.6 24实现第4个目标r3下的用户可以自动获取ip
[r3]dhcp enable
[r3]ip pool r3
[r3-ip-pool-r3]network 192.168.1.96 mask 27
[r3-ip-pool-r3]gateway-list 192.168.1.97
[r3-ip-pool-r3]dns-list 144.144.144.144 8.8.8.8
[r3-ip-pool-r3]int g 0/0/2
[r3-GigabitEthernet0/0/2]dhcp select global 
检测:
pc1:

pc2:

配置缺省路由





ping 内网


避免环路,需要配置空接口
空接口配置:




现在内网都做通了,现在需要做的是访问外网
所以在R5g0/0/2接口做个acl






 首先打开R1的telnet服务:
首先打开R1的telnet服务:
定义账号作用

 R4,R5配置备用线路:
R4,R5配置备用线路:

 R4与R5正常通过1000M链路,故障时通过100m链路;
R4与R5正常通过1000M链路,故障时通过100m链路;
 R6 telnet 12.0.0.5 登录到R1
R6 telnet 12.0.0.5 登录到R1
相关文章:

静态路由实验
1.实验拓扑图 二、实验要求 1.R6为ISP,接口IP地址均为公有地址,该设备只能配置IP地址,之后不能再对其进行任何配置; 2.R1-R5为局域网,私有IP地址192.168.1.0/24,请合理分配; 3.R1、R2、R4&…...

VSCode STM32嵌入式开发插件记录
要卸载之前搭建的VSCode嵌入式开发环境了,记录一下用的插件。 1.Cortex-Debug https://github.com/Marus/cortex-debug 2.Embedded IDE https://github.com/github0null/eide 3.Keil uVision Assistant https://github.com/jacksonjim/keil-assistant/ 4.RTO…...

linux cpu 占用超100% 分析。
感谢: https://www.cnblogs.com/wolfstark/p/16450131.html 总结: 查看进程中各个线程占用百分比 top -H -p <pid> 某线程100%了 说明 任务处理不过来 会卡 但是永远不可能超100% 系统监视器里面看到的是 所有线程占用的 总和会超100%。 所以最好的情况是&…...

自然学习法和科学学习法
一、自然学习法 自然学习法:什么事自然学习法,特意让kimi来回答了一下。所谓的自然学习法说的俗一点就是野路子学习方法。这种学习方法的特点是“慢”“没有系统性”,学完之后感觉都会了,但是又感觉什么都不会。 二、科学学习法 …...
力扣第二十四题——两两交换链表中的节点
内容介绍 给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。 示例 1: 输入:head [1,2,3,4] 输出ÿ…...

C语言柔性数组详解
目录 1.柔性数组 2.柔性数组的特点 3.柔性数组的使用 4.柔性数组的优势 1.柔性数组 C99 中,结构体中的最后一个元素允许是未知大小的数组,这就叫做『柔性数组』成员。 例如: struct S {char c;int n;int arr[];//柔性数组 }; struct …...
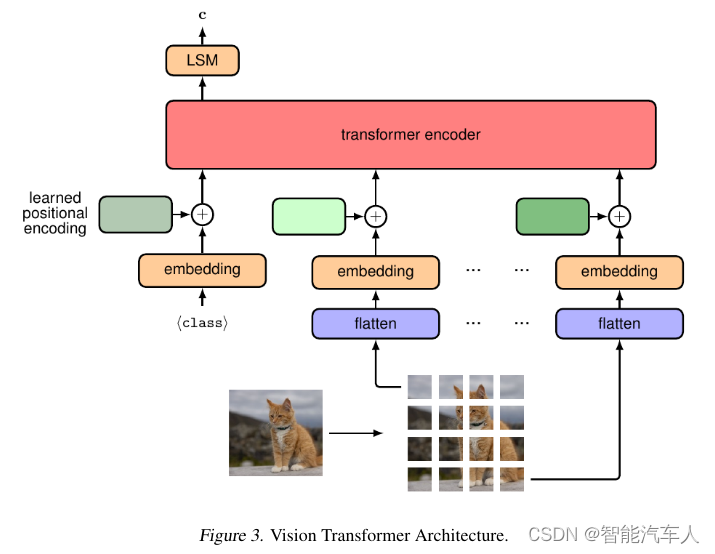
自动驾驶---视觉Transformer的应用
1 背景 在过去的几年,随着自动驾驶技术的不断发展,神经网络逐渐进入人们的视野。Transformer的应用也越来越广泛,逐步走向自动驾驶技术的前沿。笔者也在博客《人工智能---什么是Transformer?》中大概介绍了Transformer的一些内容:…...

预训练语言模型实践笔记
Roberta output_hidden_statesTrue和last_hidden_states和pooler_output 在使用像BERT或RoBERTa这样的transformer模型时,output_hidden_states和last_hidden_state是两个不同的概念。 output_hidden_states: 这是一个布尔值,决定了模型是否应该返回所…...

Perl 哈希
Perl 哈希 Perl 哈希是一种强大的数据结构,用于存储键值对集合。它是 Perl 语言的核心特性之一,广泛应用于各种编程任务中。本文将详细介绍 Perl 哈希的概念、用法和最佳实践。 什么是 Perl 哈希? Perl 哈希是一种关联数组,其中…...

Linux之Mysql索引和优化
一、MySQL 索引 索引作为一种数据结构,其用途是用于提升数据的检索效率。 1、索引分类 - 普通索引(INDEX):索引列值可重复 - 唯一索引(UNIQUE):索引列值必须唯一,可以为NULL - 主键索引(PRIMARY KEY):索引列值必须唯一,不能为NULL,一个表只能有一个主键索引 - 全…...

springboot业务逻辑写在controller层吗
Spring Boot中的业务逻辑不应该直接写在Controller层。 在Spring Boot项目中,通常将业务逻辑分为几个层次,包括Controller层、Service层、Mapper层和Entity层。 1.其中,Controller层主要负责处理HTTP请求,通过注…...

Ubuntu 24.04 LTS 桌面安装MT4或MT5 (MetaTrader)教程
运行脚本即可在 Ubuntu 24.04 LTS Noble Linux 上轻松安装 MetaTrader 5 或 4 应用程序,使用 WineHQ 进行外汇交易。 MetaTrader 4 (MT4) 或 MetaTrader 5 是用于交易外汇对和商品的流行平台。它支持各种外汇经纪商、内置价格分析工具以及通过专家顾问 (EA) 进行自…...

Go基础编程 - 12 -流程控制
流程控制 1. 条件语句1.1. if...else 语句1.2. switch 语句1.3. select 语句1.3.1. select 语句的通信表达式1.3.2. select 的基特性1.3.3. select 的实现原理1.3.4. 经典用法1.3.4.1 超时控制1.3.4.2 多任务并发控制1.3.4.3 监听多通道消息1.3.4.4 default 实现非堵塞读写 2. …...

汽车信息安全--TLS,OpenSSL
目录 TLS相关知识 加密技术 对称加密 非对称加密 数字签名和CA 信任链 根身份证和自签名 双方TLS认证 加密和解密的性能 TLS相关知识 加密技术 TLS依赖两种加密技术 1. 对称加密(symmetric encryption) 2. 非对称加密(asymmetri…...
与左模糊匹配(LIKE LEFT))
深入探索 SQL 中的 LIKE 右模糊匹配(LIKE RIGHT)与左模糊匹配(LIKE LEFT)
引言 在数据库操作中,LIKE 子句是执行模糊搜索的强大工具,用于匹配列中的数据与指定的模式。本文将详细介绍 LIKE 子句中的两种常用模式:右模糊匹配(LIKE RIGHT)和左模糊匹配(LIKE LEFT)&#…...

mybatis 多数据源 TDataSource required a single bean, but 2 were found
情况说明: 项目中本来就有一个数据源了,运行的好好的后来又合并了另一个项目,另一个项目也配置了数据源。 于是出现了如下错误: mybatis 多数据源 TDataSource required a single bean, but 2 were found 解决方法:…...

Dubbo SPI 之路由器
1. 背景介绍 Dubbo 是一个高性能的 Java RPC 框架,由阿里巴巴开源并广泛应用于分布式系统中。在 Dubbo 的架构中,SPI(Service Provider Interface)是一个关键组件,允许在运行时动态加载不同的服务实现。SPI 机制提供了…...
Python深度学习环境配置(Pytorch、CUDA、cuDNN),包括Anaconda搭配Pycharm的环境搭建以及基础使用教程(保姆级教程,适合小白、深度学习零基础入门)
全流程导览 一、前言二、基本介绍2.1全过程软件基本介绍2.1.1 Pytorch2.1.2 Anaconda2.1.3 Pycharm2.1.4 显卡GPU及其相关概念2.1.5 CUDA和cuDNN 2.2 各部分相互间的联系和安装逻辑关系 三、Anaconda安装3.1安装Anaconda3.2配置环境变量3.3检验是否安装成功 四、Pycharm安装五、…...
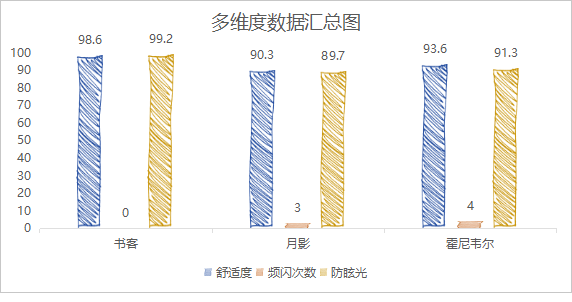
月影护眼大路灯怎么样?书客|月影|霍尼韦尔超硬核实力性能测评pk!
月影护眼大路灯怎么样?选到专业优质的护眼大路灯是真的可以使我们在用眼时减少疲劳感,达到护眼效果,但如果不慎买到劣质的护眼灯产品,不仅达不到健康的环境光,还越用越觉得眼睛疲劳感加重,在水深的护眼灯市…...
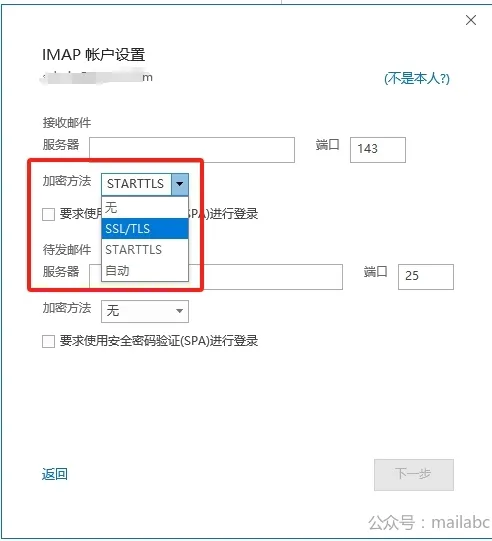
邮件安全篇:邮件传输加密(SSL/TLS or STATRTTLS)
1. 前言 使用过邮件客户端的同学一定见过下面这张图。这是客户端账号配置界面,里面有SSL、STARTTLS选项。刚接触邮件客户端的同学肯定会有这些疑问:什么是SSL?什么是STARTTLS?两者有什么区别?具体该如何选择呢&#x…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...
