轨迹优化 | 基于ESDF的共轭梯度优化算法(附ROS C++/Python仿真)
目录
- 0 专栏介绍
- 1 数值优化:共轭梯度法
- 2 基于共轭梯度法的轨迹优化
- 2.1 障碍约束函数
- 2.2 曲率约束函数
- 2.3 平滑约束函数
- 3 算法仿真
- 3.1 ROS C++实现
- 3.2 Python实现
0 专栏介绍
🔥课程设计、毕业设计、创新竞赛、学术研究必备!本专栏涉及更高阶的运动规划算法实战:曲线生成与轨迹优化、碰撞模型与检测、多智能体群控、深度强化学习运动规划、社会性导航、全覆盖路径规划等内容,每个模型都包含代码实现加深理解。
🚀详情:运动规划实战进阶
1 数值优化:共轭梯度法
共轭梯度法是一种用于解决大型稀疏线性方程组或无约束优化问题的迭代数值方法。它利用了线性代数中的共轭概念,并结合了梯度下降法的思想,以更有效地找到函数的极小值点。

形式化地,对于 n n n维二次优化问题
x ∗ = a r g min x 1 2 x T Q x + q T x \boldsymbol{x}^*=\mathrm{arg}\min _{\boldsymbol{x}}\frac{1}{2}\boldsymbol{x}^T\boldsymbol{Qx}+\boldsymbol{q}^T\boldsymbol{x} x∗=argxmin21xTQx+qTx
其中 Q \boldsymbol{Q} Q是 n n n维对称正定阵, q ∈ R n \boldsymbol{q}\in \mathbb{R} ^n q∈Rn,共轭梯度法既克服了梯度下降法收敛慢的缺点,又避免存储和计算牛顿类算法所需的二阶梯度信息,其核心原理是:求解矩阵 Q \boldsymbol{Q} Q的共轭向量组 d 0 , d 1 , ⋯ , d n \boldsymbol{d}_0,\boldsymbol{d}_1,\cdots ,\boldsymbol{d}_n d0,d1,⋯,dn作为 n n n个优化方向,由于优化方向间彼此正交,故每次迭代只需沿着一个方向 d i \boldsymbol{d}_i di寻优而互不影响。所以理论上最多 n n n次迭代就能找到最优解,收敛速度快,但实际应用中需要视具体情况确定阈值。
2 基于共轭梯度法的轨迹优化
对路径序列 X = { x i = ( x i , y i ) ∣ i ∈ [ 1 , N ] } \mathcal{X} =\left\{ \boldsymbol{x}_i=\left( x_i,y_i \right) |i\in \left[ 1,N \right] \right\} X={xi=(xi,yi)∣i∈[1,N]}设计优化目标函数
f ( X ) = w o P o b s ( X ) + w κ P c u r ( X ) + w s P s m o ( X ) f\left( \mathcal{X} \right) =w_oP_{\mathrm{obs}}\left( \mathcal{X} \right) +w_{\kappa}P_{\mathrm{cur}}\left( \mathcal{X} \right) +w_sP_{\mathrm{smo}}\left( \mathcal{X} \right) f(X)=woPobs(X)+wκPcur(X)+wsPsmo(X)
2.1 障碍约束函数
P o b s ( X ) = ∑ x i ∈ X σ o ( ∥ x i − o min ∥ 2 − d max ) P_{\mathrm{obs}}\left( \mathcal{X} \right) =\sum_{\boldsymbol{x}_i\in \mathcal{X}}^{}{\sigma _o\left( \left\| \boldsymbol{x}_i-\boldsymbol{o}_{\min} \right\| _2-d_{\max} \right)} Pobs(X)=xi∈X∑σo(∥xi−omin∥2−dmax)
惩罚机器人与障碍发生碰撞,其中 σ o ( ⋅ ) \sigma _o\left( \cdot \right) σo(⋅)是惩罚函数(可选为二次型); o min \boldsymbol{o}_{\min} omin是距离 x i \boldsymbol{x}_i xi最近的障碍物; d max d_{\max} dmax是距离阈值,节点与最近障碍物的距离超过阈值则不会受到惩罚。以二次型为例,其梯度为
∂ P o b s ( x i ) ∂ x i = 2 ( ∥ x i − o min ∥ 2 − d max ) ∂ ∥ x i − o min ∥ 2 ∂ x i = 2 ( ∥ x i − o min ∥ 2 − d max ) x i − o min ∥ x i − o min ∥ 2 \frac{\partial P_{\mathrm{obs}}\left( \boldsymbol{x}_i \right)}{\partial \boldsymbol{x}_i}=2\left( \left\| \boldsymbol{x}_i-\boldsymbol{o}_{\min} \right\| _2-d_{\max} \right) \frac{\partial \left\| \boldsymbol{x}_i-\boldsymbol{o}_{\min} \right\| _2}{\partial \boldsymbol{x}_i}\\=2\left( \left\| \boldsymbol{x}_i-\boldsymbol{o}_{\min} \right\| _2-d_{\max} \right) \frac{\boldsymbol{x}_i-\boldsymbol{o}_{\min}}{\left\| \boldsymbol{x}_i-\boldsymbol{o}_{\min} \right\| _2} ∂xi∂Pobs(xi)=2(∥xi−omin∥2−dmax)∂xi∂∥xi−omin∥2=2(∥xi−omin∥2−dmax)∥xi−omin∥2xi−omin
这里最小障碍通过ESDF获取,可以参考相关文章:
- ROS2从入门到精通5-1:详解代价地图与costmap插件编写(以距离场ESDF为例)
- 轨迹优化 | 图解欧氏距离场与梯度场算法(附ROS C++/Python实现)

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-toB9MWvL-1721696975312)(https://i-blog.csdnimg.cn/direct/2da70f16131b48e2a2dfb8e1cbf7a89b.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBATXIuV2ludGVyYA==,size_50,color_FFFFFF,t_30,g_se,x_16#pic_center =650x)]
2.2 曲率约束函数
P c u r ( X ) = ∑ x i ∈ X σ κ ( Δ ϕ i ∥ Δ x i ∥ 2 − κ max ) P_{\mathrm{cur}}\left( \mathcal{X} \right) =\sum_{\boldsymbol{x}_i\in \mathcal{X}}^{}{\sigma _{\kappa}\left( \frac{\varDelta \phi _i}{\left\| \varDelta \boldsymbol{x}_i \right\| _2}-\kappa _{\max} \right)} Pcur(X)=xi∈X∑σκ(∥Δxi∥2Δϕi−κmax)
对每个节点轨迹的瞬时曲率进行了上界约束,其中 σ κ ( ⋅ ) \sigma _{\kappa}\left( \cdot \right) σκ(⋅)是惩罚函数(可选为二次型); 是路径最大允许曲率——由机器人转向半径约束决定
其梯度为
∂ P c u r ( x i ) ∂ x i = α 1 ∂ κ i ∂ x i − 1 + α 2 ∂ κ i ∂ x i + α 3 ∂ κ i ∂ x i + 1 \frac{\partial P_{\mathrm{cur}}\left( \boldsymbol{x}_i \right)}{\partial \boldsymbol{x}_i}=\alpha _1\frac{\partial \kappa _i}{\partial \boldsymbol{x}_{i-1}}+\alpha _2\frac{\partial \kappa _i}{\partial \boldsymbol{x}_i}+\alpha _3\frac{\partial \kappa _i}{\partial \boldsymbol{x}_{i+1}} ∂xi∂Pcur(xi)=α1∂xi−1∂κi+α2∂xi∂κi+α3∂xi+1∂κi
为了求解该梯度,定义向量 a \boldsymbol{a} a在向量 b \boldsymbol{b} b的垂直分量为
a ⊥ b = a − a T b ∣ b ∣ ⋅ b ∣ b ∣ \boldsymbol{a}\bot \boldsymbol{b}=\boldsymbol{a}-\frac{\boldsymbol{a}^T\boldsymbol{b}}{\left| \boldsymbol{b} \right|}\cdot \frac{\boldsymbol{b}}{\left| \boldsymbol{b} \right|} a⊥b=a−∣b∣aTb⋅∣b∣b
则令
p 1 = Δ x i ⊥ ( − Δ x i + 1 ) ∥ Δ x i ∥ 2 ∥ Δ x i + 1 ∥ 2 , p 2 = ( − Δ x i + 1 ) ⊥ Δ x i ∥ Δ x i ∥ 2 ∥ Δ x i + 1 ∥ 2 \boldsymbol{p}_1=\frac{\varDelta \boldsymbol{x}_i\bot \left( -\varDelta \boldsymbol{x}_{i+1} \right)}{\left\| \varDelta \boldsymbol{x}_i \right\| _2\left\| \varDelta \boldsymbol{x}_{i+1} \right\| _2}, \boldsymbol{p}_2=\frac{\left( -\varDelta \boldsymbol{x}_{i+1} \right) \bot \varDelta \boldsymbol{x}_i}{\left\| \varDelta \boldsymbol{x}_i \right\| _2\left\| \varDelta \boldsymbol{x}_{i+1} \right\| _2} p1=∥Δxi∥2∥Δxi+1∥2Δxi⊥(−Δxi+1),p2=∥Δxi∥2∥Δxi+1∥2(−Δxi+1)⊥Δxi
从而
∂ κ i ∂ x i = 1 ∥ Δ x i ∥ 2 − 1 1 − cos 2 Δ ϕ ( − p 1 − p 2 ) − Δ ϕ i Δ x i ∥ Δ x i ∥ 2 3 ∂ κ i ∂ x i − 1 = 1 ∥ Δ x i ∥ 2 − 1 1 − cos 2 Δ ϕ p 2 + Δ ϕ i Δ x i ∥ Δ x i ∥ 2 3 ∂ κ i ∂ x i + 1 = 1 ∥ Δ x i ∥ 2 − 1 1 − cos 2 Δ ϕ p 1 \begin{aligned} \frac{\partial \kappa _i}{\partial \boldsymbol{x}_i}&=\frac{1}{\left\| \varDelta \boldsymbol{x}_i \right\| _2}\frac{-1}{\sqrt{1-\cos ^2\varDelta \phi}}\left( -\boldsymbol{p}_1-\boldsymbol{p}_2 \right) -\frac{\varDelta \phi _i\varDelta \boldsymbol{x}_i}{\left\| \varDelta \boldsymbol{x}_i \right\| _{2}^{3}}\\\frac{\partial \kappa _i}{\partial \boldsymbol{x}_{i-1}}&=\frac{1}{\left\| \varDelta \boldsymbol{x}_i \right\| _2}\frac{-1}{\sqrt{1-\cos ^2\varDelta \phi}}\boldsymbol{p}_2+\frac{\varDelta \phi _i\varDelta \boldsymbol{x}_i}{\left\| \varDelta \boldsymbol{x}_i \right\| _{2}^{3}}\\\frac{\partial \kappa _i}{\partial \boldsymbol{x}_{i+1}}&=\frac{1}{\left\| \varDelta \boldsymbol{x}_i \right\| _2}\frac{-1}{\sqrt{1-\cos ^2\varDelta \phi}}\boldsymbol{p}_1\end{aligned} ∂xi∂κi∂xi−1∂κi∂xi+1∂κi=∥Δxi∥211−cos2Δϕ−1(−p1−p2)−∥Δxi∥23ΔϕiΔxi=∥Δxi∥211−cos2Δϕ−1p2+∥Δxi∥23ΔϕiΔxi=∥Δxi∥211−cos2Δϕ−1p1
2.3 平滑约束函数
P s m o ( X ) = ∑ x i ∈ X ∥ Δ x i − Δ x i + 1 ∥ 2 2 P_{\mathrm{smo}}\left( \mathcal{X} \right) =\sum_{\boldsymbol{x}_i\in \mathcal{X}}^{}{\left\| \varDelta \boldsymbol{x}_i-\varDelta \boldsymbol{x}_{i+1} \right\| _{2}^{2}} Psmo(X)=xi∈X∑∥Δxi−Δxi+1∥22
期望每段轨迹的长度近似相等,使整体运动更平坦,其梯度为
∂ P s m o ( x i ) ∂ x i = 2 ( x i − 2 − 4 x i − 1 + 6 x i − 4 x i + 1 + x i + 2 ) \frac{\partial P_{\mathrm{smo}}\left( \boldsymbol{x}_i \right)}{\partial \boldsymbol{x}_i}=2\left( \boldsymbol{x}_{i-2}-4\boldsymbol{x}_{i-1}+6\boldsymbol{x}_i-4\boldsymbol{x}_{i+1}+\boldsymbol{x}_{i+2} \right) ∂xi∂Psmo(xi)=2(xi−2−4xi−1+6xi−4xi+1+xi+2)
3 算法仿真
3.1 ROS C++实现
核心算法如下所示:
bool CGOptimizer::optimize(Points2d& path_o)
{// distance map updateboost::shared_ptr<costmap_2d::DistanceLayer> distance_layer;bool is_distance_layer_exist = false;for (auto layer = costmap_ros_->getLayeredCostmap()->getPlugins()->begin();layer != costmap_ros_->getLayeredCostmap()->getPlugins()->end(); ++layer){distance_layer = boost::dynamic_pointer_cast<costmap_2d::DistanceLayer>(*layer);if (distance_layer){is_distance_layer_exist = true;break;}}if (!is_distance_layer_exist)ROS_ERROR("Failed to get a Distance layer for potentional application.");int iter = 0;while (iter < max_iter_){// choose the first three nodes of the pathfor (int i = 2; i < path_o.size() - 2; ++i){Eigen::Vector2d xi_c2(path_o[i - 2].first, path_o[i - 2].second);Eigen::Vector2d xi_c1(path_o[i - 1].first, path_o[i - 1].second);Eigen::Vector2d xi(path_o[i].first, path_o[i].second);Eigen::Vector2d xi_p1(path_o[i + 1].first, path_o[i + 1].second);Eigen::Vector2d xi_p2(path_o[i + 2].first, path_o[i + 2].second);Eigen::Vector2d correction = Eigen::Vector2d::Zero();correction = correction + _calObstacleTerm(xi, distance_layer);if (!_insideMap((xi - correction)[0], (xi - correction)[1]))continue;correction = correction + _calSmoothTerm(xi_c2, xi_c1, xi, xi_p1, xi_p2);if (!_insideMap((xi - correction)[0], (xi - correction)[1]))continue;correction = correction + _calCurvatureTerm(xi_c1, xi, xi_p1);if (!_insideMap((xi - correction)[0], (xi - correction)[1]))continue;Eigen::Vector2d gradient = alpha_ * correction / (w_obstacle_ + w_smooth_ + w_curvature_);if (std::isnan(gradient[0]) || std::isnan(gradient[1]))gradient = Eigen::Vector2d::Zero();xi = xi - gradient;path_o[i] = std::make_pair(xi[0], xi[1]);}iter++;}return true;
}


3.2 Python实现
核心算法如下所示:
while i < self.max_iter:for j in range(2, pts_num - 2):xjm2 = np.array([[optimized_path[j - 2][0]], [optimized_path[j - 2][1]]])xjm1 = np.array([[optimized_path[j - 1][0]], [optimized_path[j - 1][1]]])xj = np.array([[optimized_path[j][0]], [optimized_path[j][1]]])xjp1 = np.array([[optimized_path[j + 1][0]], [optimized_path[j + 1][1]]])xjp2 = np.array([[optimized_path[j + 2][0]], [optimized_path[j + 2][1]]])gradient = np.zeros((2, 1))# obstacle avoidancegradient = gradient + self.obstacleTerm(xj)if not self.isOnGrid(xj - gradient):continue# smoothgradient = gradient + self.smoothTerm(xjm2, xjm1, xj, xjp1, xjp2)if not self.isOnGrid(xj - gradient):continue# curvaturegradient = gradient + self.curvatureTerm(xjm1, xj, xjp1)if not self.isOnGrid(xj - gradient):continuexj = xj - self.alpha * gradient / self.w_totaloptimized_path[j, :] = xj[:, 0]i += 1self.trajectory = optimized_path

完整工程代码请联系下方博主名片获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …
相关文章:

轨迹优化 | 基于ESDF的共轭梯度优化算法(附ROS C++/Python仿真)
目录 0 专栏介绍1 数值优化:共轭梯度法2 基于共轭梯度法的轨迹优化2.1 障碍约束函数2.2 曲率约束函数2.3 平滑约束函数 3 算法仿真3.1 ROS C实现3.2 Python实现 0 专栏介绍 🔥课程设计、毕业设计、创新竞赛、学术研究必备!本专栏涉及更高阶的…...
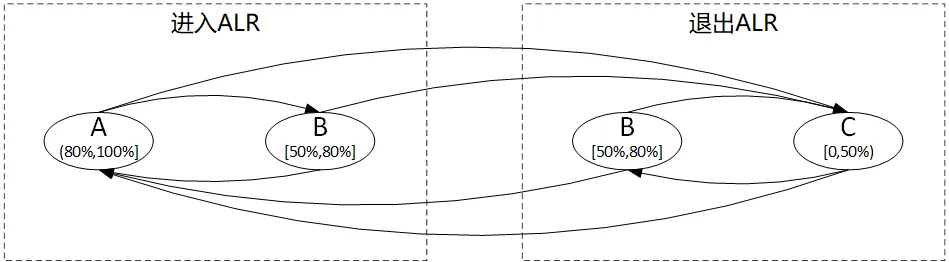
深入浅出WebRTC—ALR
ALR(Application Limited Region)指的是网络传输过程中,由于应用层的限制(而非网络拥塞)导致带宽未被充分利用的情况。在这种情况下,应用层可能因为处理能力、手动配置或其他因素无法充分利用可用带宽&…...

BSV区块链技术现实应用原理解析
BSV区块链以其卓越的可扩展性、坚如磐石的安全性、极低的交易成本等特性,成为满足企业当下需求并为企业未来成功奠基铺路的理想技术。 BSV协会近期发布了一个题为《驾驭数字化转型:在自动化世界中建立信任——区块链在数据保护和交易优化中的角色》的报…...

七大基于比较的排序算法
目录 一、基于比较的排序算法概述 1. 插入排序(Insertion Sort) 2. 选择排序(Selection Sort) 3. 冒泡排序(Bubble Sort) 4. 归并排序(Merge Sort) 5. 快速排序(Qu…...
)
web前端 React 框架面试200题(四)
面试题 97. React 两种路由模式的区别?hash和history? 参考回答: 1: hash路由 hash模式是通过改变锚点(#)来更新页面URL,并不会触发页面重新加载,我们可以通过window.onhashchange监听到hash的改变,从而处…...
5.Fabric的共识机制
在Fabric中,有以下3中典型共识机制。 Solo共识 solo共识机制只能用于单节点模式,即只能有一个Orderer节点,因此,其共识过程很简单,每接收到一个交易信息,就在共识模块的控制下产生区块并广播给节点存储到账本中。 Solo 模式下的共识只适用于一个Orderer节点,所以可以在…...

【safari】react在safari浏览器中,遇到异步时间差的问题,导致状态没有及时更新到state,引起传参错误。如何解决
在safari浏览器中,可能会遇到异步时间差的问题,导致状态没有及时更新到state,引起传参错误。 PS:由于useState是一个普通的函数, 定义为() > void;因此此处不能用await/async替代setTimeout,只能用在返…...

京准:GPS北斗卫星授时信号安全隔离防护装置
京准:GPS北斗卫星授时信号安全隔离防护装置 京准:GPS北斗卫星授时信号安全隔离防护装置 1、主要特点 ★信号加固功能: GPS/BDS单系统信号拒止情况下(包含受到GPS L1欺骗干扰、GPS L1压制干扰、BDS B1欺骗干扰、BDS B1压制干扰&…...

解决方案架构师系列 - AWS - Pinpoint
AWS Pinpoint介绍 Amazon Pinpoint 为营销人员和开发人员提供了一款可自定义的工具,助力他们大规模地开展跨渠道、行业和活动的客户通信。 Amazon Pinpoint是一个全面的客户参与平台,旨在帮助营销人员和开发人员大规模地开展跨渠道、行业和活动的客…...
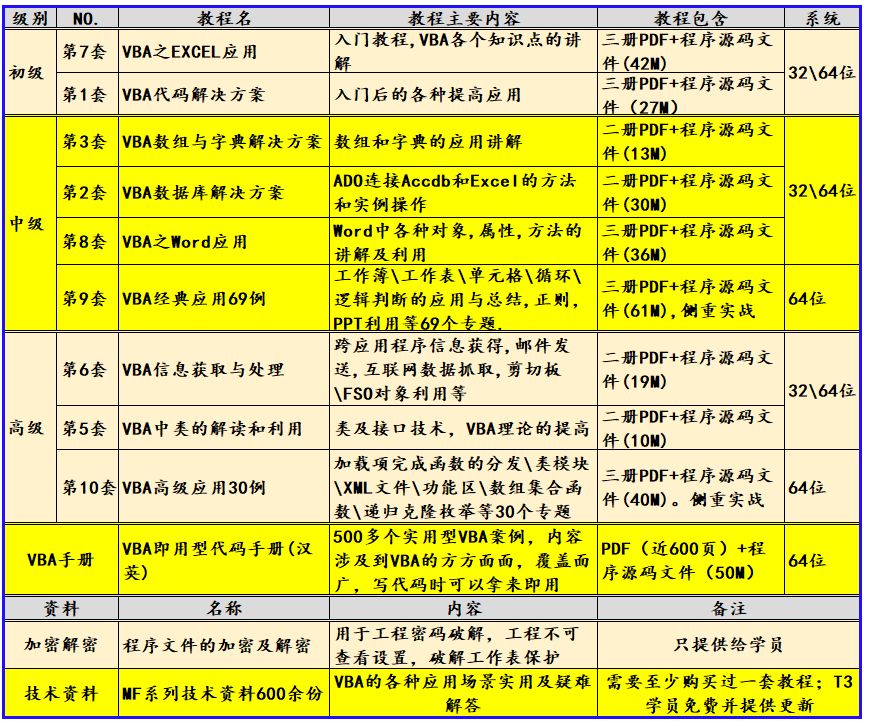
MF173:将多个工作表转换成PDF文件
我给VBA的定义:VBA是个人小型自动化处理的有效工具。利用好了,可以大大提高自己的工作效率,而且可以提高数据的准确度。“VBA语言専攻”提供的教程一共九套,分为初级、中级、高级三大部分,教程是对VBA的系统讲解&#…...

Docker、containerd、CRI-O 和 runc 之间的区别
容器与 Docker 这个名称并不紧密相关。你可以使用其他工具来运行容器 您可以使用 Docker 或一堆非Docker 的其他工具来运行容器。docker只是众多选项之一,Docker(公司)在生态系统中创建了一些很棒的工具,但不是全部。 容器方面有…...

PRISM-Python 中的规则一个简单的 Python 规则感应系统
欢迎来到雲闪世界.PRISM 是一种现有算法(尽管我确实创建了一个 Python 实现),PRISM 相对简单,但在机器学习中,有时最复杂的解决方案效果最好,有时最简单的解决方案效果最好。然而,当我们希望建立…...

DB-GPT:LLM应用的集大成者
整体架构 架构解读 可以看到,DB-GPT把架构抽象为7层,自下而上分别为: 运行环境:支持本地/云端&单机/分布式等部署方式。顺便一提,RAY是蚂蚁深度参与的一个开源项目,所以对RAY功能的支持应该非常完善。…...
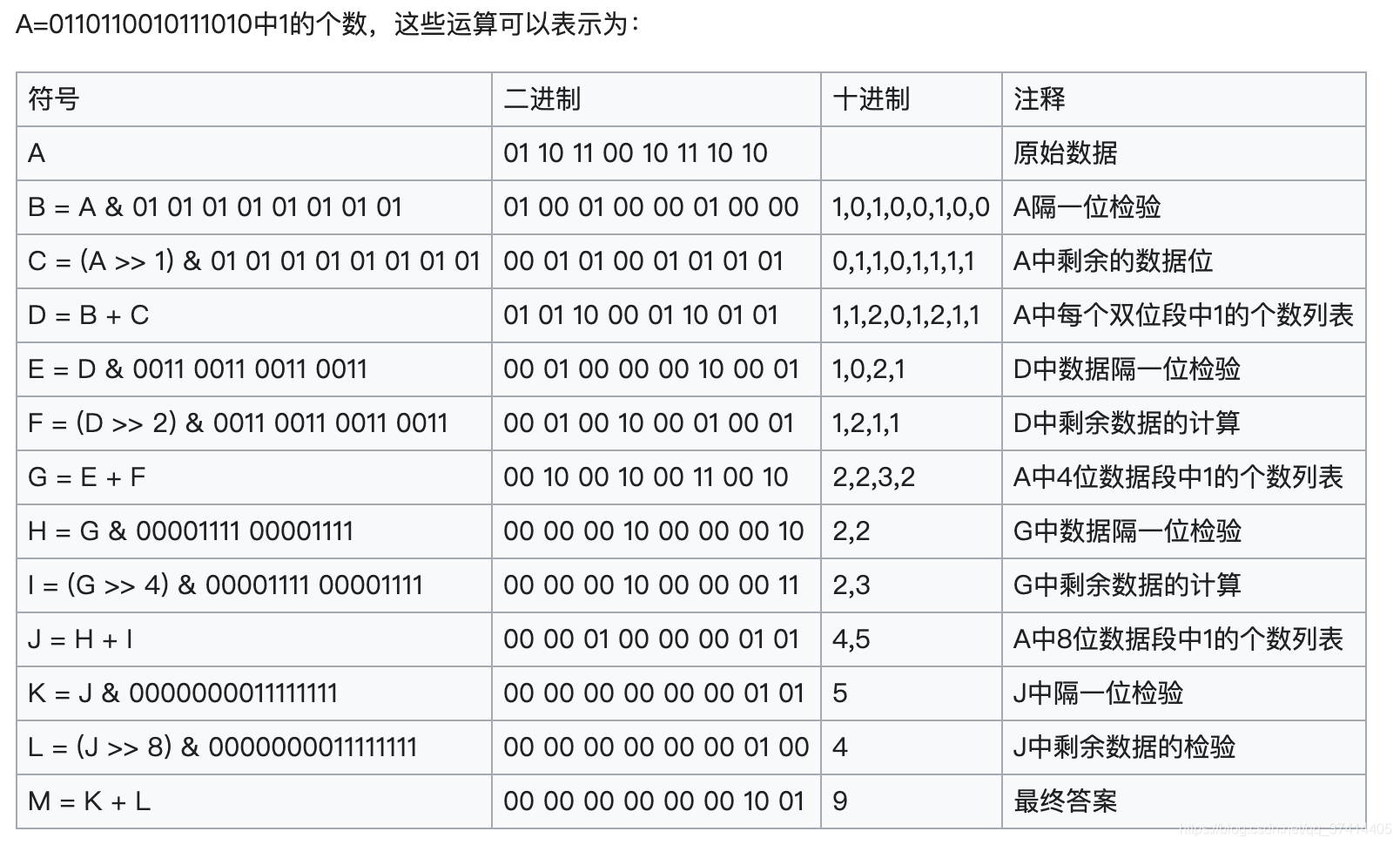
汉明权重(Hamming Weight)(统计数据中1的个数)VP-SWAR算法
汉明权重(Hamming Weight)(统计数据中1的个数)VP-SWAR算法 定义 汉明重量是一串符号中非零符号的个数。它等于同样长度的全零符号串的汉明距离(在信息论中,两个等长字符串之间的汉明距离等于两个字符串对应位置的不同…...

基于 PyTorch 的模型瘦身三部曲:量化、剪枝和蒸馏,让模型更短小精悍!
基于 PyTorch 的模型量化、剪枝和蒸馏 1. 模型量化1.1 原理介绍1.2 PyTorch 实现 2. 模型剪枝2.1 原理介绍2.2 PyTorch 实现 3. 模型蒸馏3.1 原理介绍3.2 PyTorch 实现 参考文献 1. 模型量化 1.1 原理介绍 模型量化是将模型参数从高精度(通常是 float32࿰…...

二、原型模式
文章目录 1 基本介绍2 实现方式深浅拷贝目标2.1 使用 Object 的 clone() 方法2.1.1 代码2.1.2 特性2.1.3 实现深拷贝 2.2 在 clone() 方法中使用序列化2.2.1 代码 2.2.2 特性 3 实现的要点4 Spring 中的原型模式5 原型模式的类图及角色5.1 类图5.1.1 不限制语言5.1.2 在 Java 中…...

【目标检测】Anaconda+PyTorch(GPU)+PyCharm(Yolo5)配置
前言 本文主要介绍在windows系统上的Anaconda、PyTorch、PyCharm、Yolov5关键步骤安装,为使用yolo所需的环境配置完善。同时也算是记录下我的配置流程,为以后用到的时候能笔记查阅。 Anaconda 软件安装 Anaconda官网:https://www.anaconda…...

Django实战项目之进销存数据分析报表——第二天:项目创建和 PyCharm 配置
在上一篇博客中,我们讨论了如何搭建一个全栈 Web 应用的开发环境,包括 Python 环境的创建、Django 和 MySQL 的安装以及前端技术栈的选择。现在,让我们继续深入,学习如何在 PyCharm 中创建一个新的 Django 项目并进行配置。 一…...

静态路由实验
1.实验拓扑图 二、实验要求 1.R6为ISP,接口IP地址均为公有地址,该设备只能配置IP地址,之后不能再对其进行任何配置; 2.R1-R5为局域网,私有IP地址192.168.1.0/24,请合理分配; 3.R1、R2、R4&…...

VSCode STM32嵌入式开发插件记录
要卸载之前搭建的VSCode嵌入式开发环境了,记录一下用的插件。 1.Cortex-Debug https://github.com/Marus/cortex-debug 2.Embedded IDE https://github.com/github0null/eide 3.Keil uVision Assistant https://github.com/jacksonjim/keil-assistant/ 4.RTO…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...

医疗AI模型可解释性编程研究:基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践,在这一过程中,模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法(如RandomForest、XGBoost、LightGBM)因其卓越的预测性能和相对良好的解释性…...
