【数据结构】还不懂算法复杂度?一文带你速解
前言:
前面我们已经系统的学完C语言的相关知识,现在我们已经较为熟练的掌握了C语言中的各中代码语法和结构使用,能够使用代码来解决一些简单问题。但是对于一个程序员来说,仅仅会语法是远远不够的,从今天开始,我们将进入到数据结构的学习。
一、初始数据结构:
数据结构:
数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的 数据元素的集合。通常情况下,精心选择的数据结构可以带来更高的运行和存储效率。数据结构往往同高效的检索算法和索引技术有关。
2.算法:
算法(Algorithm):就是定义良好的计算过程,它取一个或一组的值为输入,病残生出一个或一组值作为输出。见来说算就是一系列计算步骤用来将输入数据转化为输出结果。
算法具有以下五个特点:
①有穷性:指算法必须能在执行有限个步骤之后终止;
②确切性:算法的每一个步骤必须有确切的定义;
③输入项:一个算法有0个或者多个输入,以刻画运算对象的初始情况,所谓0个输入是指算法本身定出了初始条件;
④输出项:一个算法有一个或多个输出,以反映对输入数据加工后的结果;
⑤可行性:算法中执行的任何计算机步骤都是可以被分解为基本的可执行的操作步骤,即每个计算步骤都快要有限时间内完成。
常见的算法思想:递推法、递归法、穷举法、贪心算法、分治法、动态规划法、迭代法、分支界限法,回溯法。
二、算法效率:
算法的效率可以分为两种:时间效率和空间效率。
时间效率顾名思义就是指算法执行的时间,依据改算法编制的程序在计算机上运行时所消耗的时间来度量。空间效率指的是程序运行所需占用的空间,根据该算法编制的程序在计算机上运行时所占用的全部空间来度量。总而言之,算法效率其实就是为了研究算法的好坏而生的。而我们在衡量算法的好坏时,通常从时间和空间这两个角度出发的。从时间维度出发研究算法的时间复杂度,从空间维度出发研究算法的空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算 机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计 算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
时间复杂度:
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间,一个算法执行所消耗的时间,从理论上讲是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道,但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,而且随着科技的发展,现在不同的电脑cpu差距很大,又可能在一个电脑跑10s的程序,到另一个电脑就需要15s了,所以才有了时间复杂的这个分析方式。一个算法所花费的时间于其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
即:找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。
例如:
/ 请计算一下Func1中++count语句总共执行了多少次?
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
{for (int j = 0; j < N ; ++ j){++count;}
}for (int k = 0; k < 2 * N ; ++ k)
{++count;
}
int M = 10;
while (M--)
{++count;
}
上述代码中,第一部分的嵌套循环共执行了N的平方(N^2);第二部分的循环共执行了N*2次,第三部分共执行了10次,因此这段代码的时间复杂度F(N):
F(N)=N^2+N*2+10
也就是:
N = 10 F(N) = 130 N = 100 F(N) = 10210 N = 1000 F(N) = 1002010
但是在实际中,我们在计算时间复杂度时,并不一定要计算精确的执行次数(从上面的示例我们就可发现,随着N增大,时间复杂度与N*2+10的关系越来越小,时间复杂度取决于最高次幂N^2),而只需要大概执行次数就可以了,于是我们通常用大O的渐进表示法来表示算法的时间复杂度。
2.大O渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶
例如上面的时间复杂度使用此方法表示为:O(N^2)。即通过使用此方法,去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界) 平均情况:任意输入规模的期望运行次数 最好情况:任意输入规模的最小运行次数(下界) 例如:在一个长度为N数组中搜索一个数据x 最好情况:1次找到 最坏情况:N次找到 平均情况:N/2次找到
而在我们在实际中的一般情况下关注的是算法的最坏运行情况。
3.空间复杂度:
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。 空间复杂度不是程序占用了多少bytes的空间,因为对于如今的技术这个也没太大意义,所以空间复杂度算的是变量的个数。 空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进表示法。 注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因 此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
例如:
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
在上述代码中,出去原本就存在的的量的空间外,额外定义的变量有end、i和exchange,共三个,则空间复杂度的表达式F(N)=3;其表达式为常数,大O表示为O(1);
总结:
今天是我们初识数据结构,到此我们对数据结构有了一个大致的了解,同时学会了计算算法的时间复杂度和空间复杂度,学会这两个我们就可以更加精确的优化我们的代码。
本文仍有许多不足,欢迎各位随时批评指正。
相关文章:

【数据结构】还不懂算法复杂度?一文带你速解
前言:前面我们已经系统的学完C语言的相关知识,现在我们已经较为熟练的掌握了C语言中的各中代码语法和结构使用,能够使用代码来解决一些简单问题。但是对于一个程序员来说,仅仅会语法是远远不够的,从今天开始,我们将进入…...
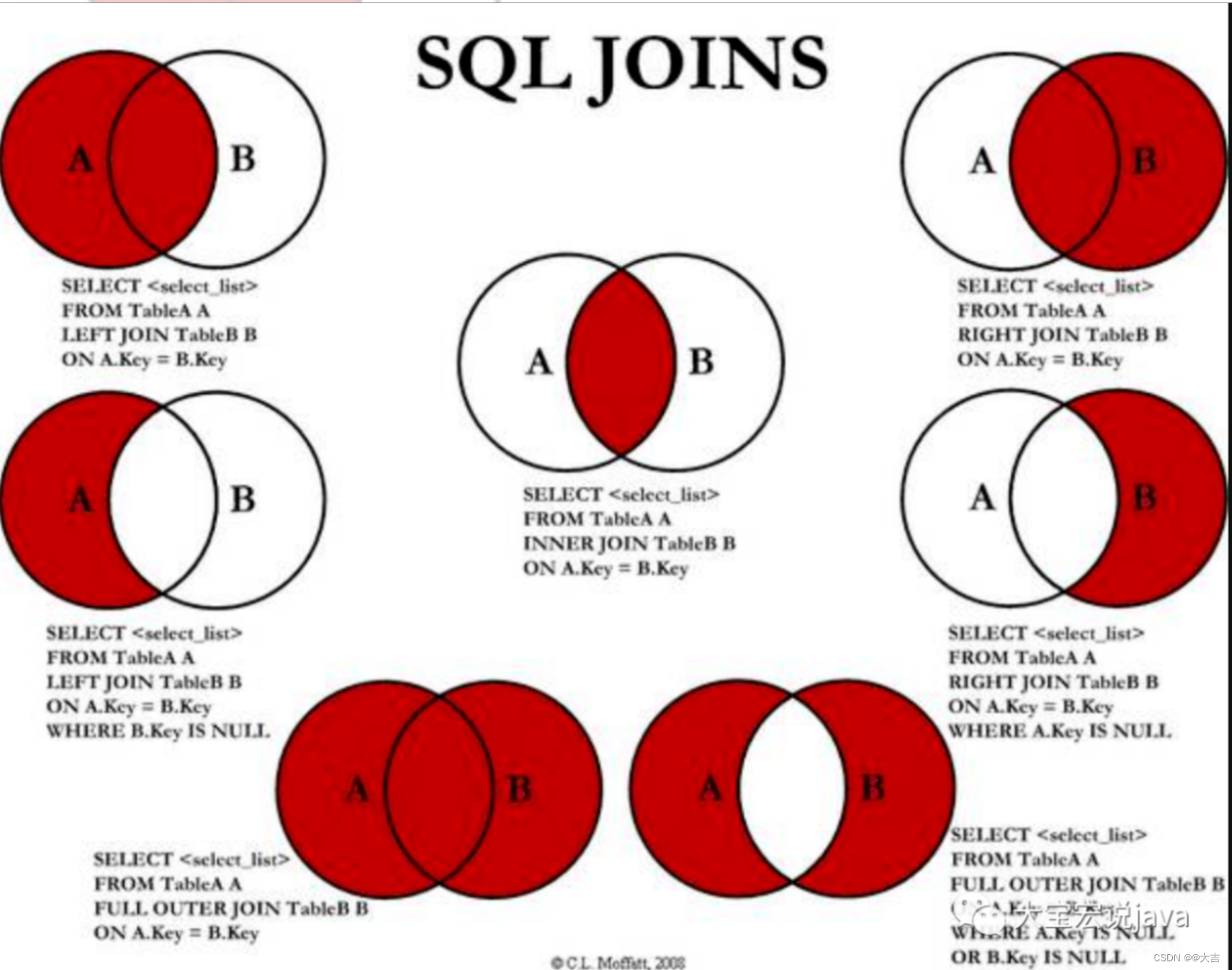
案例描述:update中,MySQL inner join 和 left join的区别,小结果集驱动大结果集
场景描述 以一个场景为例: 单据A:下游子表 (数据量级小) 单据B:下游主表(数据量级小) 单据C:中游子表(数据量级小) 单据D:中游主表(…...

CF1784D Wooden Spoon
CF1784D Wooden Spoon 题目大意 有2n2^n2n个人,进行nnn轮比赛。比赛的图是一棵完全二叉树。编号小的人一定能赢编号大的人,如果一个人满足: 第一次比赛被打败打败这个人的人在第二次比赛中被打败打败上一个人的人在第三次比赛中被打败…\d…...
【数据结构】栈
文章目录😺前言栈初始化栈顶入栈栈顶出栈栈体判空栈的数据个数获取栈顶元素栈的销毁整体代码😼写在最后😺前言 👻前面我们学习了链表,总算是跨过一个台阶了,本章带大家轻松一波,领悟一下栈的魅力…...
C++单继承和多继承
C单继承和多继承继承单继承写法继承中构造函数的写法写法构造和析构的顺序问题多继承继承 1.继承,主要是遗传学中的继承概念 2.继承的写法,继承中的权限问题 3.继承中的构造函数的写法 继承:子类没有新的属性,或者行为的产生 父类…...
金三银四,今年企业招聘如何?
又是一年求职季,互联网人找工作,和找对象一样严谨,不随便放手更不随便牵手。于是挑挑拣拣,最后的结果可能就是把自己挑剩下了。 时间已经悄然滑进3月中旬,多少无处安放的青春,还没尘埃落定?优秀…...

数字信号处理:滤波、频谱
一、滤波算法 应该说数字滤波器可以有效减小50Hz工频的干扰,完全消除是不可能的。以20ms为最小单位的整倍数周期滤波,可以有效减少工频的干扰。 软件中构建 IIR 陷波或者 FIR 带阻 数字滤波器,消除工频干扰对测量结果的影响。 1. 自适应滤波 …...
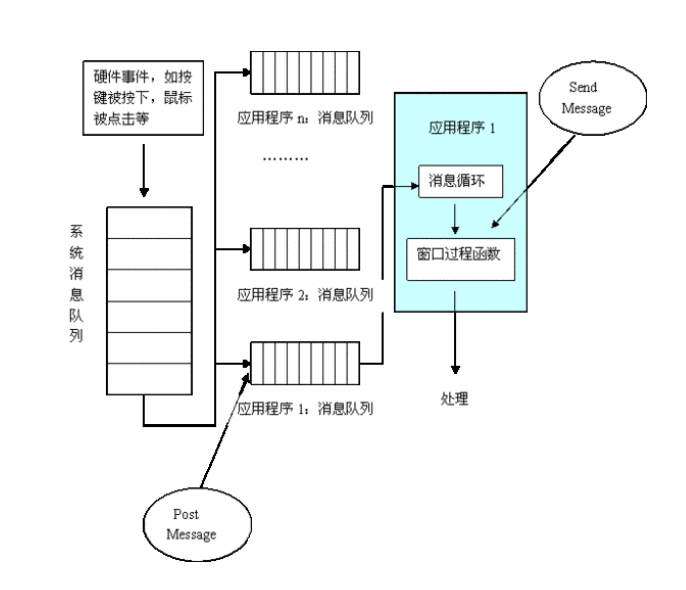
C#等高级语言运行过程
C#等高级语言运行流程:假设您编写了一个 C# 程序并将其保存在一个称为源代码的文件中。特定于语言的编译器将源代码编译成 MSIL(Microsoft 中间语言),也称为 CIL(通用中间语言)或 IL(中间语言&a…...
如何优雅的用POI导入Excel文件
在企业级项目开发中,要经常涉及excel文件和程序之间导入导出的业务要求,那么今天来讲一讲excel文件导入的实现。java实现对excel的操作有很多种方式,例如EasyExcel等,今天我们使用的是POI技术实现excel文件的导入。POI技术简介1.P…...
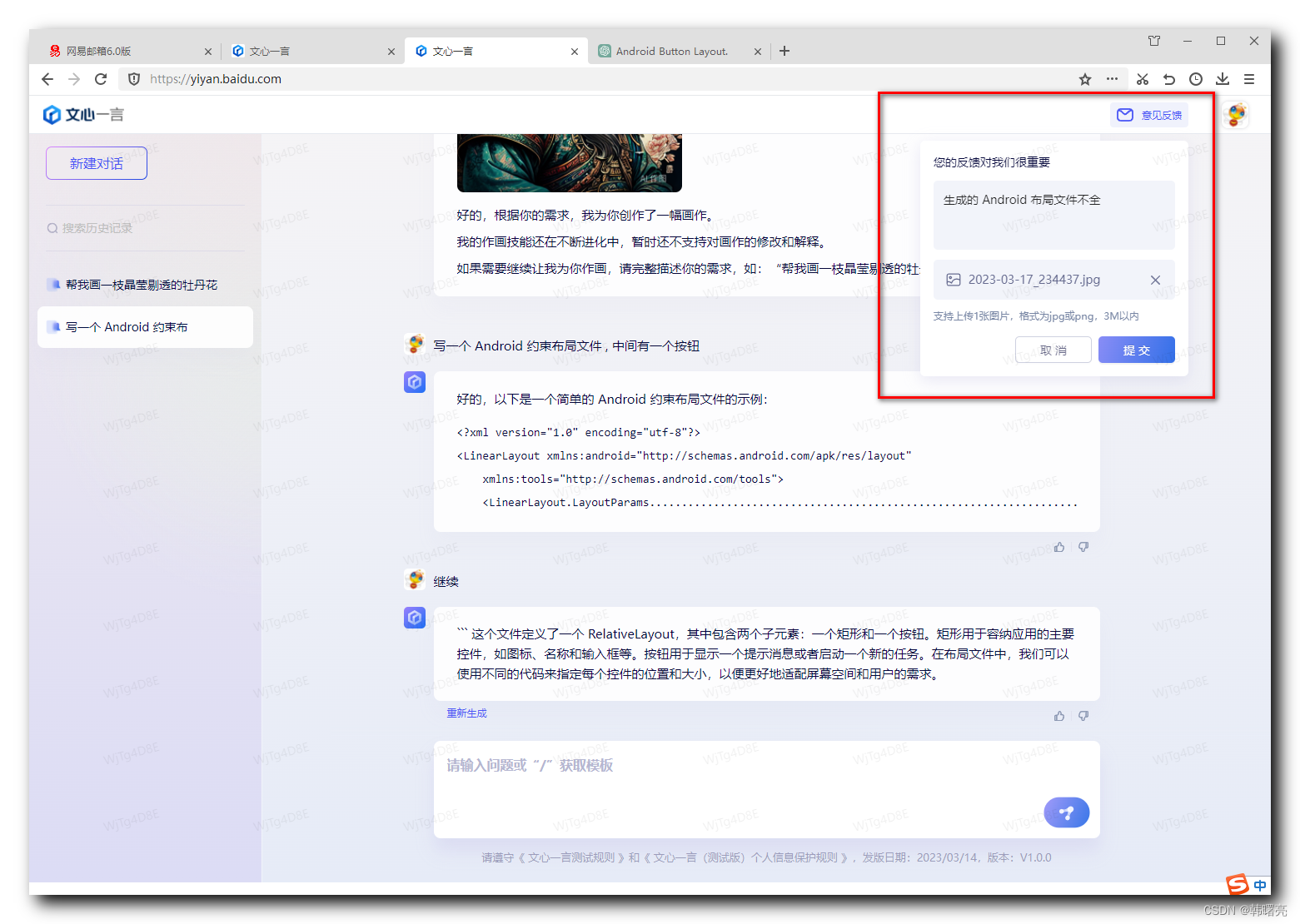
【AI 工具】文心一言内测记录
文章目录一、申请内测二、收到内测邀请三、激活内测四、开始使用1、普通对话2、生成图片3、生成代码4、写剧本5、生成小说五、问题反馈一、申请内测 到 https://yiyan.baidu.com/welcome 页面 , 点击 " 开始体验 " 按钮 , 申请试用 ; 申请时 , 需要填写相关信息 ; 主…...

Github的使用
Github Date: March 8, 2023 Sum: Github的使用 Github 了解开源相关的概念 1. 什么是开源 2. 什么是开源许可协议 开源并不意味着完全没有限制,为了限制使用者的使用范围和保护作者的权利,每个开源项目都应该遵守开源许可协议( Open Sou…...

抽丝剥茧还原真相,记一次神奇的崩溃
作者:靳倡荣 本文详细回放了一个崩溃案例的分析过程。回顾了C多态和类内存布局、pc指针与芯片异常处理、内存屏障的相关知识。 一、不讲“武德”的崩溃 1.1 查看崩溃调用栈 客户反馈了一个崩溃问题,并提供了core dump文件,查看崩溃调用栈如下…...

学习笔记八:docker资源配额
docker容器控制cpudocker容器控制cpu指定docker容器可以使用的cpu份额两个容器A、B的cpu份额分别为1000和500,结果会怎么样?给容器实例分配512权重的cpu使用份额总结CPU core核心控制扩展:服务器架构CPU配额控制参数的混合使用cpuset-cpus和c…...

小米10s格机修复 nv报错案例解析 关于基带分区的一些常识
前面分享过几期关于基带 diag端口与qcn相关的几篇帖子。其中一位粉丝朋友联系我。他的机型因为误格机导致手机进不去系统,反复进入官方rec报错nv损坏。进不去系统。 有兴趣的朋友可以参阅我的几个帖子,只是个人的一些片面理解。 基带相关贴; 安卓玩机…...
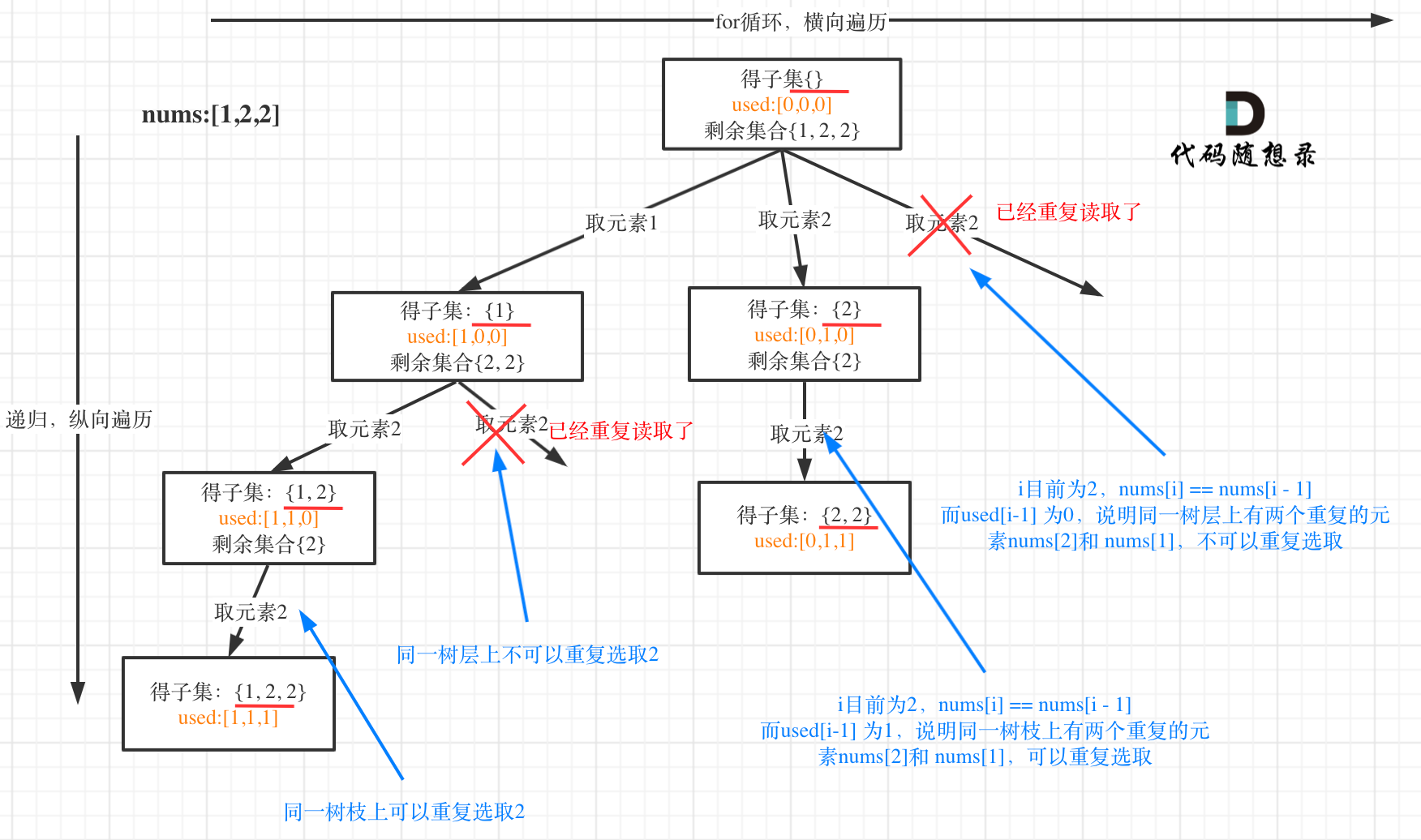
【3.17】MySQL索引整理、回溯(分割、子集问题)
3.1 索引常见面试题 索引的分类 什么是索引? 索引是一种数据结构,可以帮助MySQL快速定位到表中的数据。使用索引,可以大大提高查询的性能。 按「数据结构」分类:Btree索引、Hash索引、Full-text索引。 InnoDB 存储引擎创建的聚簇…...
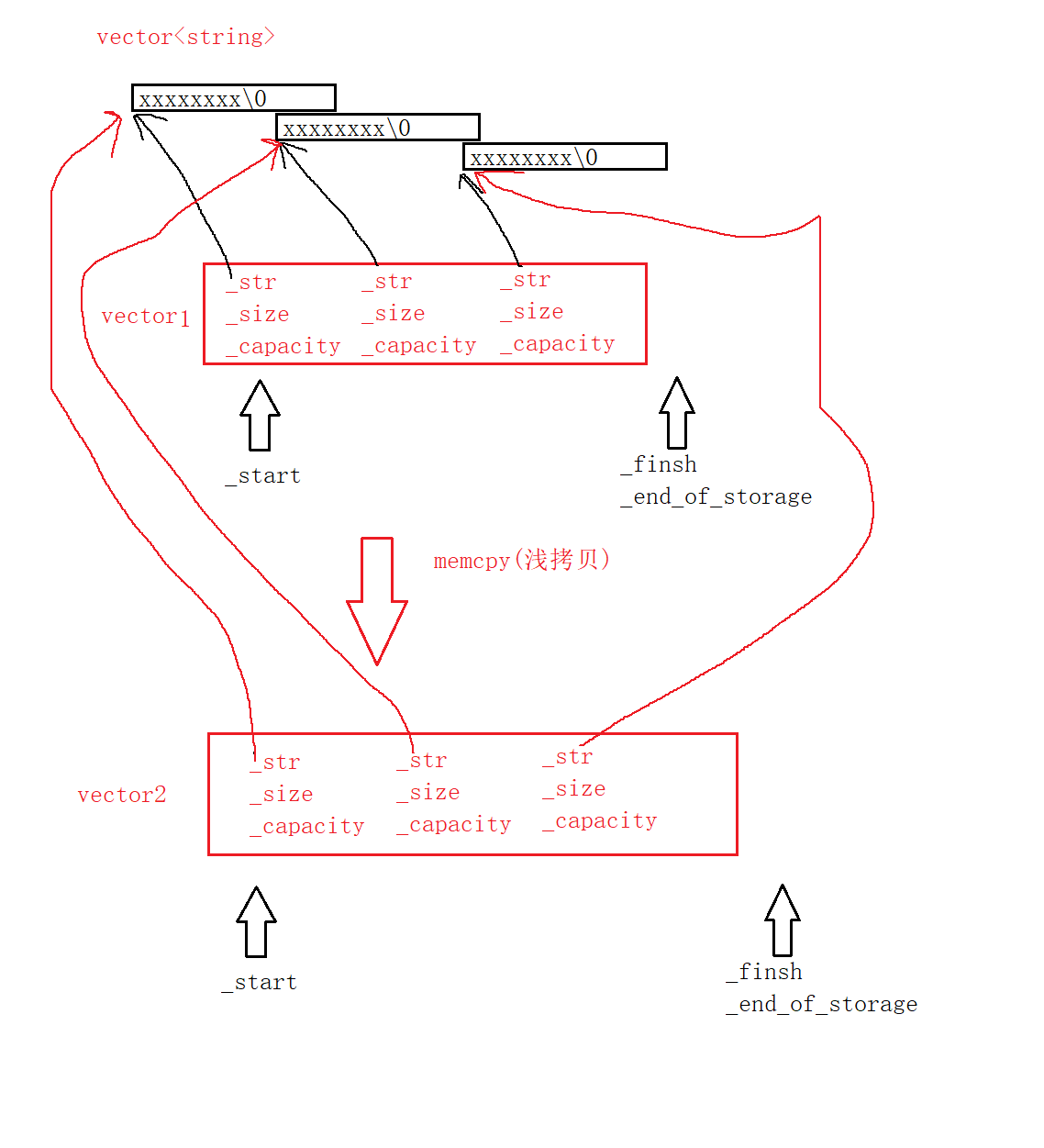
转解疑难杂症,详解vector迭代器失效和深浅拷贝的问题
前文http://t.csdn.cn/kVeVX——vector模拟实现本篇文章主要是针对vector中的两个比较经典的问题同时也是上一篇文章遗留下来的问题进行详细解释,第一个就是迭代器失效的问题,第二个是深浅拷贝的问题。ps:注意本文演示用的代码是上一篇vector…...
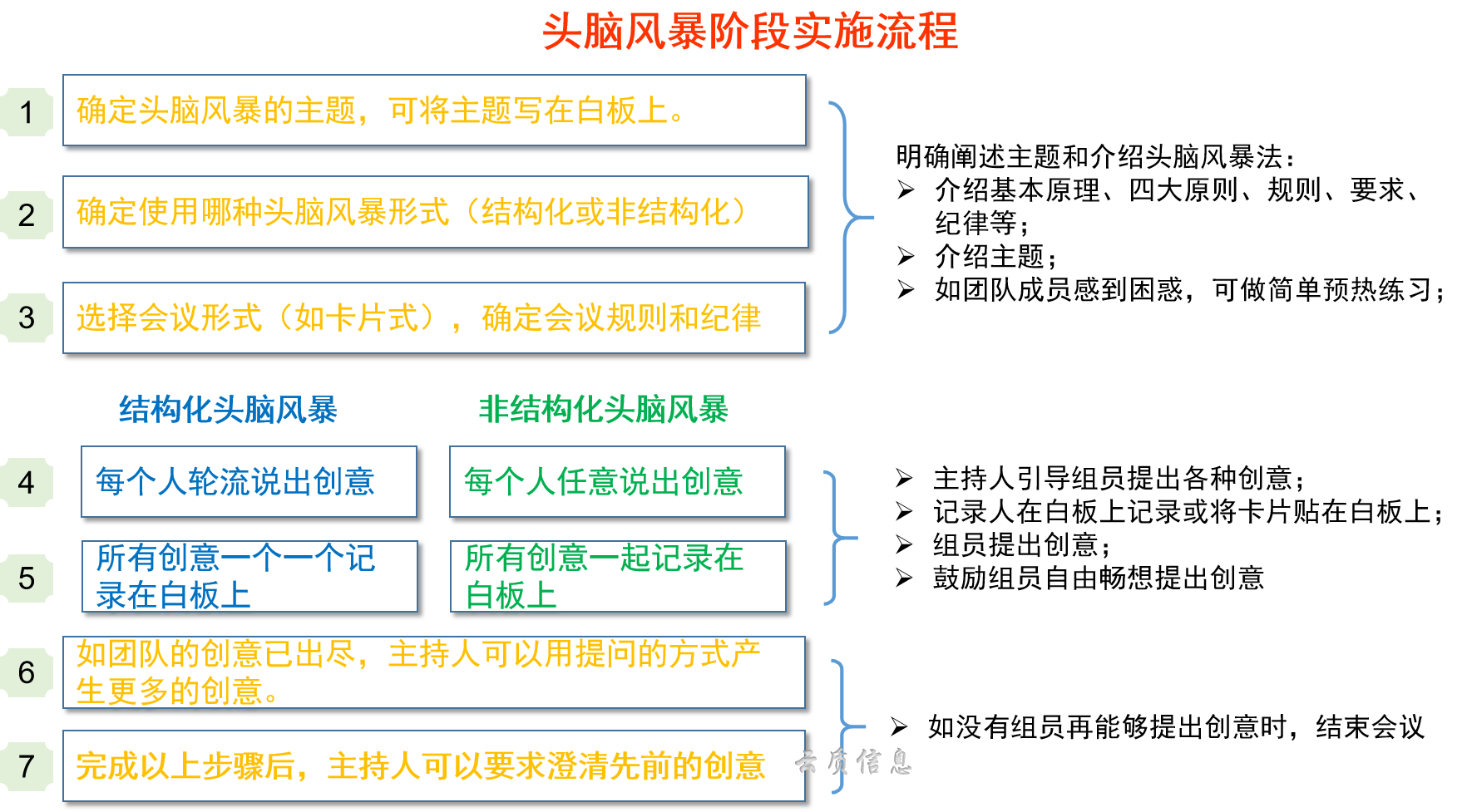
质量工具之头脑风暴法
云质QMS原创 转载请注明来源 作者:王洪石 1. 什么是头脑风暴法 头脑风暴最早是精神病理学上的用语,指的是精神病患者的精神错乱状态,后来拓展为无限制的自由联想和讨论,其目的在于产生新创意、激发新设想,或通过找到新…...

【3】核心易中期刊推荐——人工智能计算机仿真
🚀🚀🚀NEW!!!核心易中期刊推荐栏目来啦 ~ 📚🍀 核心期刊在国内的应用范围非常广,核心期刊发表论文是国内很多作者晋升的硬性要求,并且在国内属于顶尖论文发表,具有很高的学术价值。在中文核心目录体系中,权威代表有CSSCI、CSCD和北大核心。其中,中文期刊的数…...

vFlash软件简介
🍅 我是蚂蚁小兵,专注于车载诊断领域,尤其擅长于对CANoe工具的使用🍅 寻找组织 ,答疑解惑,摸鱼聊天,博客源码,点击加入👉【相亲相爱一家人】🍅 玩转CANoe&…...
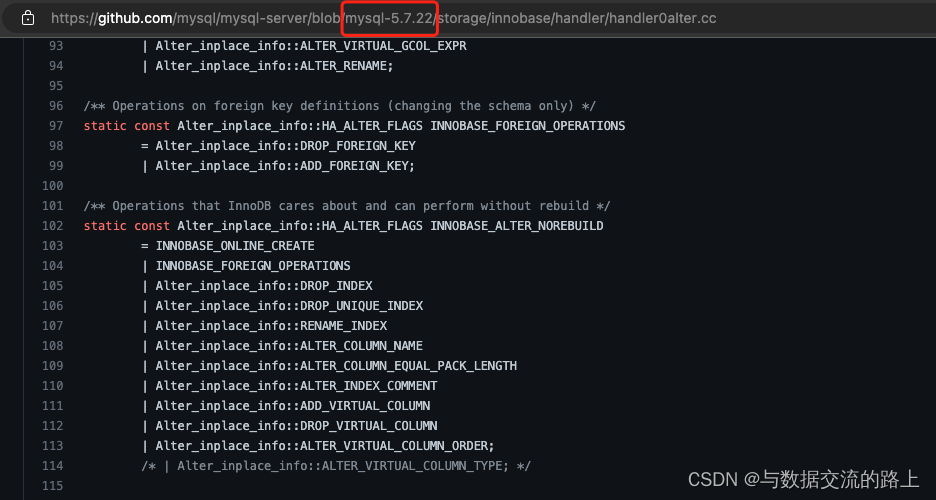
mysql-online-ddl是否需要rebuild
一、背景 DDL一直是DBA业务中的大项,看了TIDB的DDL讲解,恰巧我们的mysql业务大表也遇到了DDL的变更项,变更内容是将varchar(10)变更成varchar(20),这个变更通过官方文档很容易知道是不需要rebuild的(这里要注意下这个varchar(255…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...
