【线性代数】矩阵变换
一些特殊的矩阵
一,对角矩阵
1,什么是对角矩阵

表示将矩阵进行伸缩(反射)变换,仅沿坐标轴方向伸缩(反射)变换。
2,对角矩阵可分解为多个F1矩阵,如下:

二,剪切矩阵
1,什么是剪切矩阵




2,剪切矩阵的几何意义


3,剪切矩阵的特点
变换前后面积不变
三,正交矩阵
1,什么是正交矩阵?


2,正交矩阵的特点
(1)是方阵
(2)每个列向量都是单位矩阵
(3)每对列向量都正交
(4)正交矩阵的转置等于它的逆
3,正交矩阵的几何意义
只有旋转,无剪切,无伸缩,无反射

如下图所示,矩阵A表示绕X轴旋转60°,矩阵B表示绕Z轴旋转45°,C表示先按X轴旋转60°再按Z轴旋转45°,顺序不能颠倒。


若颠倒顺序,先绕Z轴旋转,再按X轴旋转,则:

四,投影矩阵
1,什么是投影矩阵?
将高维的变换到低维


谱分解
作用对象是对称矩阵,对称矩阵的特征向量正交。
本质:将一个复杂的变换分解为:旋转-伸缩-逆旋转


Q为单位特征向量组成的矩阵,即e1,e2,e3都是单位特征向量,为特征值组成的对角矩阵。
过程解释(以2维为例):原对称矩阵S具有2个特征向量,且特征向量都正交,矩阵实现了将特征基 e1,e2旋转到原来的基 (1,0)(0,1)的过程,然后进行
伸缩变换,即沿特征基的方向进行伸缩变换,最后再乘Q将特征基旋转回原来的位置。
谱分解的特殊点:
(1)对称矩阵的特征向量都正交,原来的基也是正交的,则仅进行正交变换(旋转)即可实现将特征基旋转为原来的基。
奇异值分解
奇异值分解与谱分解的区别只有,谱分解是旋转---伸缩---逆旋转,而奇异值分解是旋转---伸缩(可能有维度消除或维度扩充)---再旋转。奇异值分解的第二次旋转不是第一次旋转的逆旋转。
1,图+公式推导

待分解矩阵的变换如图,改变换将相互正交的向量,
变换到仍然相互正交的向量
,
,伸缩量为
,
。设
,
,
则,即
即
即
所以的特征向量为
,特征值为
同理的特征向量为
,特征值为
综上,奇异值分解中,
为
的特征向量,
为
的特征向量。
为
或
特征值的平方根。
为右奇异向量,
为左奇异向量。
2,几何解释
相关文章:
【线性代数】矩阵变换
一些特殊的矩阵 一,对角矩阵 1,什么是对角矩阵 表示将矩阵进行伸缩(反射)变换,仅沿坐标轴方向伸缩(反射)变换。 2,对角矩阵可分解为多个F1矩阵,如下: 二&a…...

聚焦智慧出行,TDengine 与路特斯科技再度携手
在全球汽车行业向电动化和智能化转型的过程中,智能驾驶技术正迅速成为行业的焦点。随着消费者对出行效率、安全性和便利性的需求不断提升,汽车制造商们需要在全球范围内实现低延迟、高质量的数据传输和处理,以提升用户体验。在此背景下&#…...

虚拟机迁移报错:虚拟机版本与主机“x.x.x.x”的版本不兼容
1.虚拟机在VCenter上从一个ESXi迁移到另一个ESXi上时报错:虚拟机版本与主机“x.x.x.x”的版本不兼容。 2.例如从10.0.128.13的ESXi上迁移到10.0.128.11的ESXi上。点击10.0.128.10上的任意一台虚拟机,查看虚拟机版本。 3.确认要迁移的虚拟机磁盘所在位…...

【教程】vscode添加powershell7终端
win10自带的 powershell 是1.0版本的,太老了,更换为powershell7后,在 vscode 的集成终端中没有显示本篇教程记录在vscode添加powershell7终端的过程 打开vscode终端配置 然后来到这个页面进行设置 查看 powershell7 的安装位置ÿ…...

如何乘上第四次工业革命的大船
如何乘上第四次工业革命的大船 第四次工业革命通常被认为是信息技术和数字化时代的到来,但具体影响哪些产业,以及它将如何演变和展开,仍然是一个广泛讨论的话题。 然而,已经可以看到一些领域可能受到第四次工业革命的深远影响,例如人工智能、物联网、大数据、生物技术、可…...

RKNN执行bash ./build-linux_RK3566_RK3568.sh 报错
目录 报错信息: 原因分析: 解决办法: 报错信息: CMake Error at /usr/share/cmake-3.22/Modules/CMakeDetermineCCompiler.cmake:49 (message): Could not find compiler set in environment variable CC: aarch64-linux-gnu-gcc. Call Stack (most recent call fir…...

Linux常用命令整理
本文将分享一些常用的Linux命令。根据功能的不同,大概分为以下几个方面,一是文件相关命令,二是进程相关命令,三是网络相关命令,四是磁盘相关命令,五是用户管理相关命令,六是系统命令。 1. 文件…...
python 闭包、装饰器
一、闭包: 1. 外部函数嵌套内部函数 2. 外部函数返回内部函数 3.内部函数可以访问外部函数局部变量 闭包(Closure)是指在一个函数内部定义的函数,并且内部函数可以访问外部函数的局部变量,即使外部函数已经执行…...

[pycharm]解决pycharm运行程序出现卡住scanning files to index索引的问题
有时候会出现索引问题,显示scanning files to index 解决方法: in pycharm, go to the "File" on the left top, then select "invalidate caches/restart...", and press "invalidate and restart". 然后等它自己重启…...
)
python每日学习11:numpy库的用法(下)
python每日学习11:numpy库的用法(下) 数组的拼接 名方法称说明concatenate连接沿现有轴的数组序列hstack水平堆叠序列中的数组(列方向)vstack竖直堆叠序列中的数组(行方向)concatenate函数用于沿指定轴连接相同形状的两…...

【Emacs有什么优点,用Emacs写程序真的比IDE更方便吗?】
🎥博主:程序员不想YY啊 💫CSDN优质创作者,CSDN实力新星,CSDN博客专家 🤗点赞🎈收藏⭐再看💫养成习惯 ✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出…...

6、基于Fabirc 2.X 通用电子存证系统部署
evidence 将GOPATH设置为/root/go,拉取项目: cd $GOPATH/src && git clone https://gitee.com/henan-minghua_0/evidence.git 在/etc/hosts中添加: 127.0.0.1 orderer.example.com 127.0.0.1 peer0.org1.example.com 127.0.0.1 peer1.org…...

Linux Vim 由浅入深的教程
引言 原文链接 Vim是Linux系统中非常强大的文本编辑器,因其强大的功能和灵活的操作而受到广泛使用。尤其是在服务器管理和开发环境中,Vim几乎是必备工具。本教程将以CentOS 7为例,详细讲解Vim的安装、基本操作以及一些高级技巧,…...

MIT6.824(6.5840) Lab1笔记+源码
文章目录 其他人的内容,笔记写的更好,思路可以去看他们的MapReduceworkermapreduce coordinatorrpc纠错 源码worker.gocoordinator.gorpc.go 原本有可借鉴的部分 mrsequential.go,多看几遍源码 其他人的内容,笔记写的更好…...
【目录】8051汇编与C语言系列教程
8051汇编与C语言系列教程 作者将狼才鲸创建日期2024-07-23 CSDN文章地址:【目录】8051汇编与C语言系列教程本Gitee仓库原始地址:才鲸嵌入式/8051_c51_单片机从汇编到C_从Boot到应用实践教程 一、本教程目录 序号教程名称简述教程链接1点亮LCD灯通过IO…...
群管机器人官网源码
一款非常好看的群管机器人html官网源码 搭建教程: 域名解析绑定 源码文件上传解压 访问域名即可 演示图片: 群管机器人官网源码下载:客户端下载 - 红客网络编程与渗透技术 原文链接: 群管机器人官网源码...

整合EasyExcel实现灵活的导入导出java
引入pom依赖 <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId></dependency>实现功能 结合Vue前端,实现浏览器页面直接导出日志文件实现文件的灵活导入文件导出 3. 实体类 实体类里有自定义转…...

springSecurity学习之springSecurity web如何取得用户信息
web如何取得用户信息 之前说过SecurityContextHolder默认使用的是ThreadLocal来进行存储的,而且每次都会清除,但是web每次请求都会验证用户权限,这是如何做到的呢? 这是通过SecurityContextPersistenceFilter来实现的࿰…...
eclipse中的classbean导入外部class文件,clean项目后删除问题
最近被eclipse搞得头疼,下午终于解决 eclipse创建的java项目中,类的输出目录是classbean。由于项目需要,classbean目录下已经导入了外部的类,但每次clean项目时,会把class删掉。 广泛查询,eclipse不清空c…...
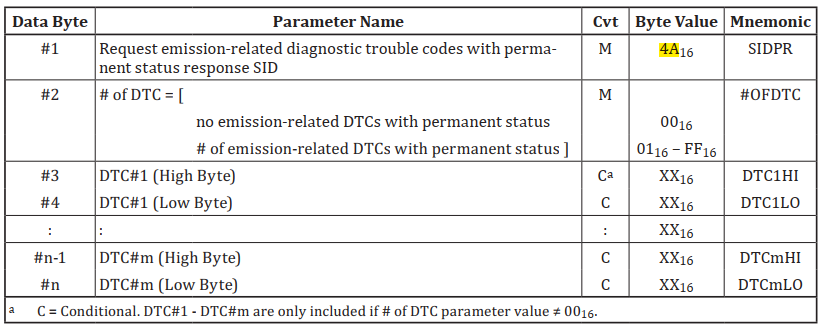
OBD诊断(ISO15031) 0A服务
文章目录 功能简介ISO 15765-4的诊断服务定义1、请求具有永久状态的排放相关故障诊断码2、请求具有永久状态的排放相关故障诊断码3、示例报文 功能简介 0A服务,即 Request emission-related diagnostic trouble code with permanent status(请求排放相关…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...
