线性代数之行列式
一、思维导图
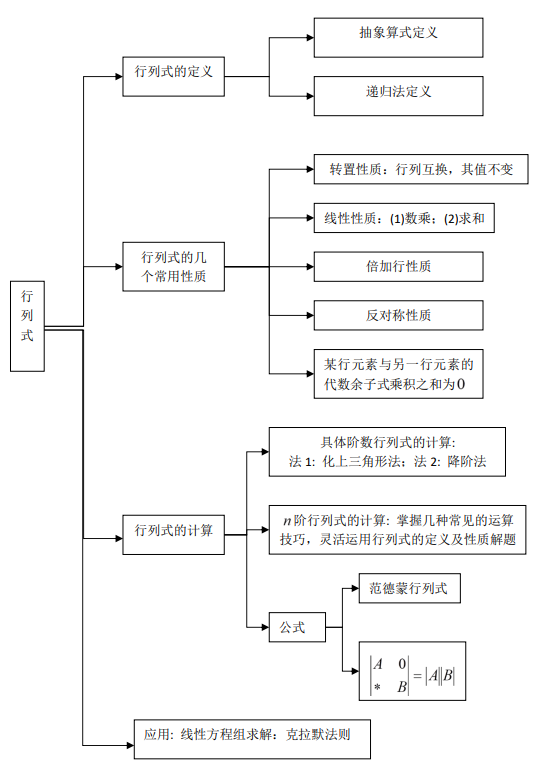
二、二阶、三阶行列式的定义
1、二阶行列式

2、三阶行列式
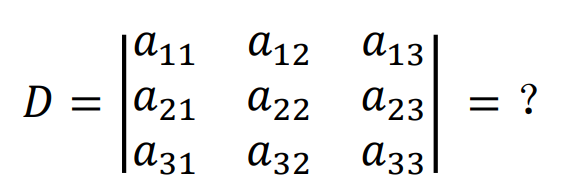
沙路法展开

3、解方程
3.1解二元一次方程组
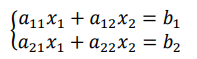
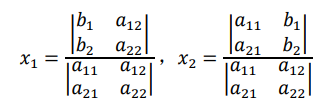
观察上面两个未知量的值不难发现,它 们的分母均是上述方程组未知量的系数形成的二阶行列式,𝑥1的分子是将系数行列 式的第一列换成了常数列其余列不变所得,𝑥2的分子是将系数行列式的第二列换 成了常数列其余列不变所得。我们将二阶行列式的这种定义法称为对角线法定义。
3.2 解三元线性方程组
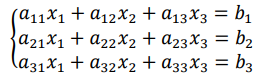

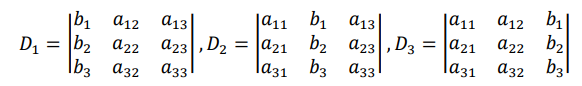
三、n阶行列式的定义
1、补充定义——排列的逆序数
• 𝒏级排列:由1, 2, … , 𝑛构成的有序数组称为一个𝒏级 排列。 • 排列的逆序:在一个排列中,如果一个较大的数 排在一个较小的数前面,则称它们构成一个逆序。
例1 在排列𝟐𝟏𝟓𝟑𝟒中,𝟐与𝟏、𝟓与𝟑、𝟓与𝟒均构成 逆序。
排列的逆序数:排列中逆序的总数称为逆序数。 注: 1. 排列 𝒋𝟏𝒋𝟐 ⋯ 𝒋𝒏 的逆序数记为: 𝛕(𝒋𝟏𝒋𝟐 ⋯ 𝒋𝒏) 2. 称逆序数为奇数的排列为奇排列,逆序数为偶 数的排列为偶排列
例:𝛕(𝟐𝟏𝟓𝟑𝟒)= 3
2、行列式的递归法定义
2.1元素的余子式、元素的代数余子式
第𝑖行第𝑗列元素𝑎𝑖𝑗的 余子式𝑀𝑖𝑗定义为去掉该元素所在的行去掉该元素所在的列,剩余元素按原来次 序排出的那个𝑛 − 1阶的行列式。
定义元素𝑎𝑖𝑗的代数余子式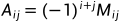 。
。
2.2 递归法定义
行列式的值=它某行元素与本行元素代数余子式的乘积之和



3、行列式的抽象算式定义法

即它的展开式为:每项由取自不同行不同列的𝑛个元素的乘积构成,每项前面的 符号由行标自然排列时列标排列的奇偶性决定。


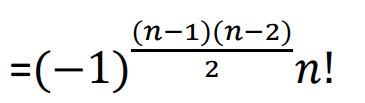
四、行列式常用的性质
性质 1 行列互换,其值不变。
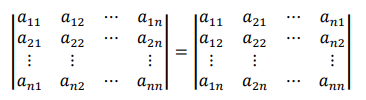
在行列式中,所有对行成立的结果,对列依 然成立。
例如下面性质 2 的描述结合性质 1 知,行列式中某列元素与其代数余 子式的乘积之和也等于此行列式的值。
性质 2 行列式中某行元素与其代数余子式的乘积之和等于此行列式的值
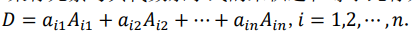
性质 3 (线性性质)
(1)数乘性质
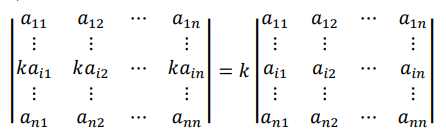
(2)求和性质

引理 若行列式中有两行元素对应相等,则其值为 0。
推论 若行列式中有两行元素对应成比例,则其值为 0。
性质 4 (倍加行性质)倍加行变换,其值不变。
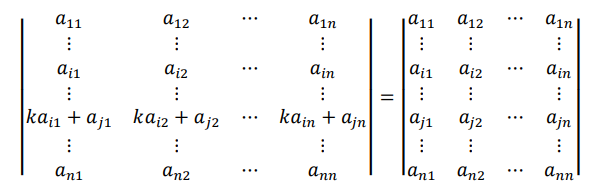
性质 5(反对称性质)两行对换,行列式的值反号
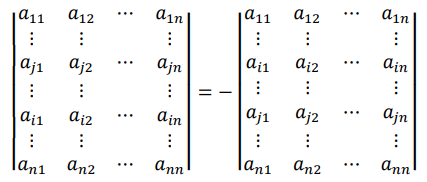
性质 6 行列式某一行的元素与另外一行元素代数余子式乘积之和为 0。
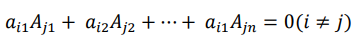
五、特殊的几个行列式
1、范德蒙行列式
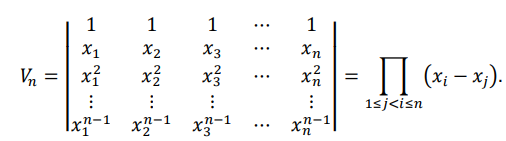

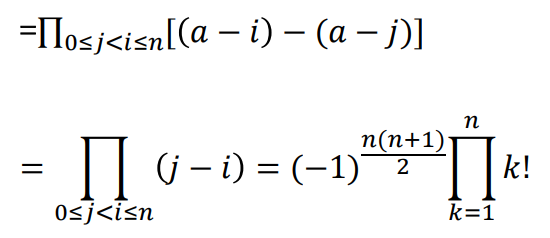
2、反对称行列式

证明:奇数阶反对称行列式的值为零。

3、几个结论


六、克莱默法则
1、定理:线性非齐次方程组
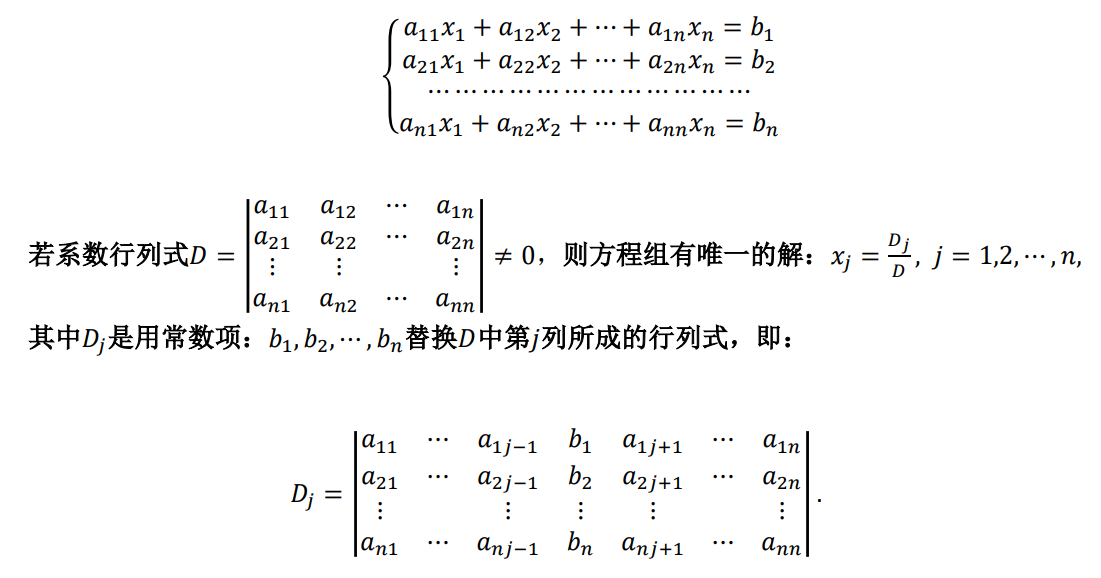
2、推论:齐次线性方程组


七、复习题

相关文章:

线性代数之行列式
一、思维导图二、二阶、三阶行列式的定义1、二阶行列式2、三阶行列式沙路法展开3、解方程3.1解二元一次方程组观察上面两个未知量的值不难发现,它 们的分母均是上述方程组未知量的系数形成的二阶行列式,𝑥1的分子是将系数行列 式的第一列换成…...

【FPGA-Spirit_V2】小精灵V2开发板初使用
🎉欢迎来到FPGA专栏~小精灵V2开发板初使用 ☆* o(≧▽≦)o *☆嗨~我是小夏与酒🍹 ✨博客主页:小夏与酒的博客 🎈该系列文章专栏:FPGA学习之旅 文章作者技术和水平有限,如果文中出现错误,希望大家…...
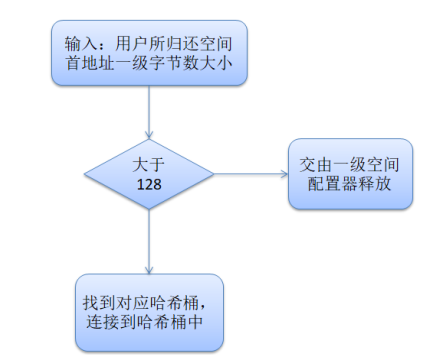
STL与其空间配置器
目录什么是STLSTL的六大组件STL的缺陷什么是空间配置器为什么需要空间配置器GI-STL空间配置器实现原理一级空间配置器二级空间配置器内存池SGI-STL中二级空间配置器设计SGI-STL二级空间配置器之空间申请前期的准备申请空间填充内存块向内存池中索要空间SGI-STL二级空间配置器之…...
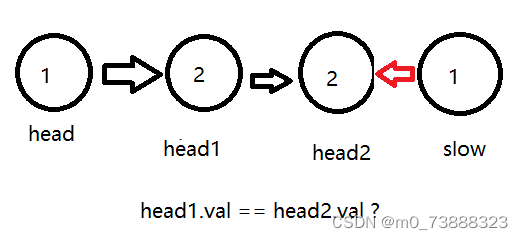
leetcode刷题之回文链表
目录 做题思路 代码实现 1.找到链表的中间节点 2.反转中间节点之后的链表 3.判断倒置的后半部分的链表是否等于前半部分的链表 整体代码展示 总结: 这里是题目链接。 这道题目的意思是:判断该链表中后半部分倒置是否跟前半部分相同,如…...

复制带随机指针的链表最长连续递增序列数组的度写字符串需要的行数最短补全词
复制带随机指针的链表来源:杭哥138. 复制带随机指针的链表 - 力扣(LeetCode)typedef struct Node Node; Node* BuyNode(int x) {Node* newnode (Node*)malloc(sizeof(Node));newnode->valx;newnode->nextNULL;newnode->randomNULL;…...

「ML 实践篇」回归系统:房价中位数预测
文章目录1. 项目分析1. 框架问题2. 性能指标2. 获取数据1. 准备工作区2. 下载数据3. 查看数据4. 创建测试集3. 数据探索1. 地理位置可视化2. 寻找相关性3. 组合属性4. 数据准备1. 数据清理2. Scikit-Learn 的设计3. 处理文本、分类属性4. 自定义转换器5. 特征缩放6. 流水线5. 选…...

深度学习 Day27——利用Pytorch实现运动鞋识别
深度学习 Day27——利用Pytorch实现运动鞋识别 文章目录深度学习 Day27——利用Pytorch实现运动鞋识别一、查看colab机器配置二、前期准备1、导入依赖项并设置GPU2、导入数据三、构建CNN网络四、训练模型1、编写训练函数2、编写测试函数3、设置动态学习率4、正式训练五、结果可…...

Springboot 整合dom4j 解析xml 字符串 转JSONObject
前言 本文只介绍使用 dom4j 以及fastjson的 方式, 因为平日使用比较多。老的那个json也能转,而且还封装好了XML,但是本文不做介绍。 正文 ①加入 pom 依赖 <dependency><groupId>dom4j</groupId><artifactId>dom4j…...

网络安全实验——安全通信软件safechat的设计
网络安全实验——安全通信软件safechat的设计 仅供参考,请勿直接抄袭,抄袭者后果自负。 仓库地址: 后端地址:https://github.com/yijunquan-afk/safechat-server 前端地址: https://github.com/yijunquan-afk/safec…...
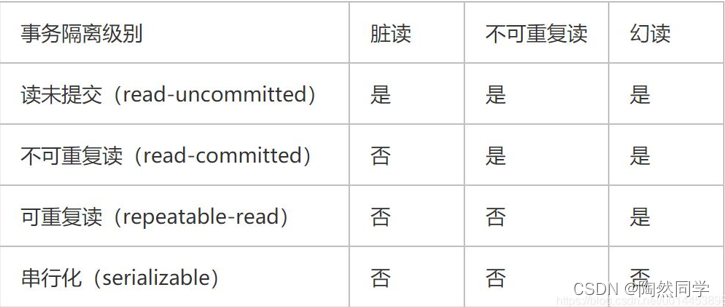
【MySQL】MySQL的事务
目录 概念 什么是事务? 理解事务 事务操作 事务的特性 事务的隔离级别 事务的隔离级别-操作 概念 数据库存储引擎是数据库底层软件组织,数据库管理系统(DBMS)使用数据引擎进行创建、查 询、更新和删除数据。 不同的存储引擎提供…...
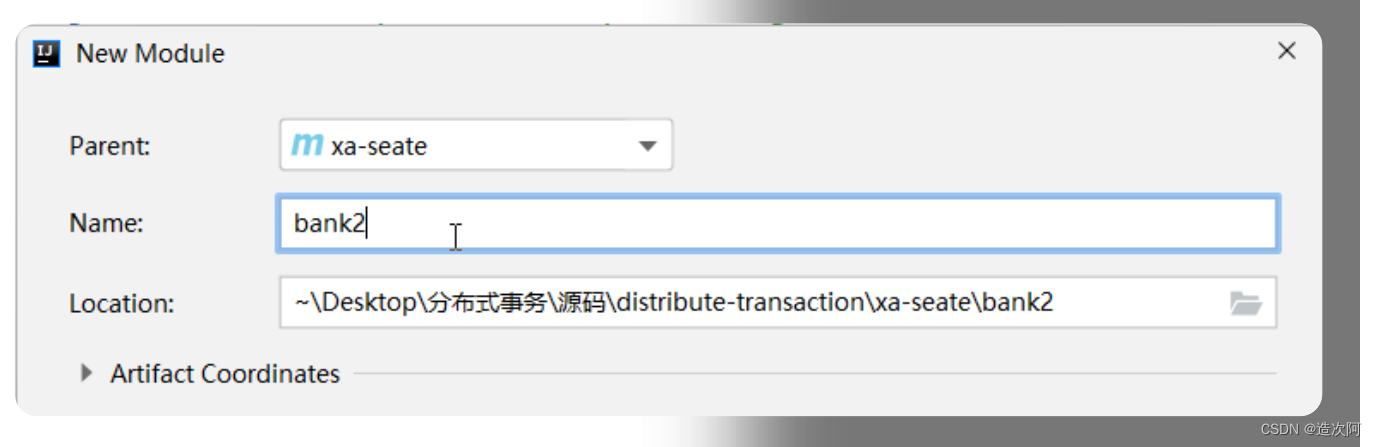
Java分布式事务(七)
文章目录🔥Seata提供XA模式实现分布式事务_业务说明🔥Seata提供XA模式实现分布式事务_下载启动Seata服务🔥Seata提供XA模式实现分布式事务_转账功能实现上🔥Seata提供XA模式实现分布式事务_转账功能实现下🔥Seata提供X…...

二十八、实战演练之定义用户类模型、迁移用户模型类
1. Django默认用户模型类 (1)Django认证系统中提供了用户模型类User保存用户的数据。 User对象是认证系统的核心。 (2)Django认证系统用户模型类位置 django.contrib.auth.models.User(3)父类AbstractUs…...

Java Virtual Machine的结构 3
1 Run-Time Data Areas 1.1 The pc Register 1.2 Java Virtual Machine Stacks 1.3 Heap 1.4 Method Area JVM方法区是在JVM所有线程中共享的内存区域,在编程语言中方法区是用于存储编译的代码、在操作系统进程中方法区是用于存储文本段,在JVM中方法…...
linux ubuntu22 安装neo4j
环境:neo4j 5 ubuntu22 openjdk-17 neo4j 5 对 jre 版本要求是 17 及以上,且最好是 openjdk,使用比较新的 ubuntu 系统安装比较好, centos7 因为没有维护,yum 找不到 openjdk-17了。 官方的 debian 系列安装教程&a…...
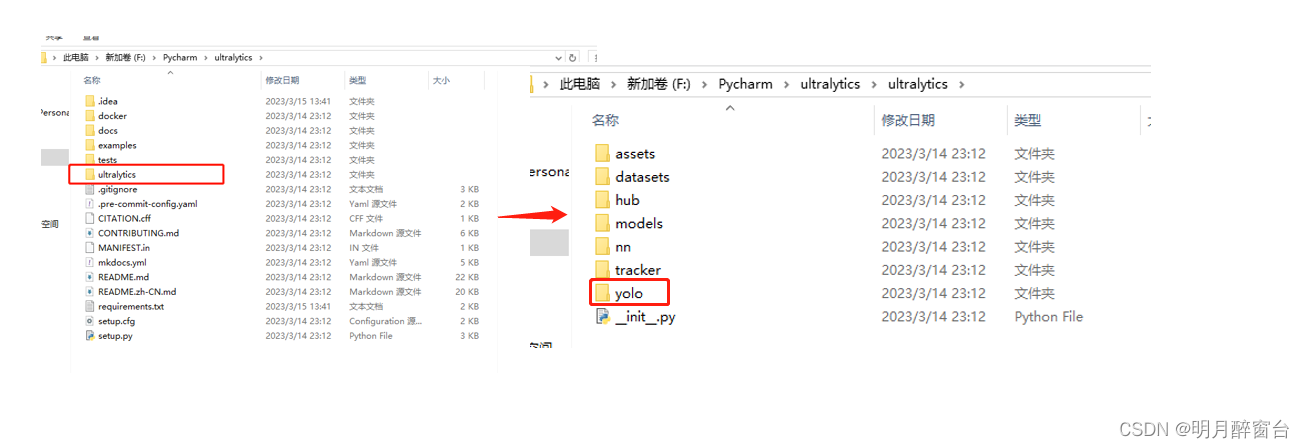
模型实战(7)之YOLOv8推理+训练自己的数据集详解
YOLOv8推理+训练自己的数据集详解 最近刚出的yolov8模型确实很赞啊,亲测同样的数据集用v5和v8两个模型训练+预测,结果显示v8在检测精度和准确度上明显强于v5。下边给出yolov8的效果对比图: 关于v8的结构原理在此不做赘述,随便搜一下到处都是。1.环境搭建 进入github进行git…...

火车进出栈问题 题解
来源 卡特兰数 个人评价(一句话描述对这个题的情感) …~%?..,# *☆&℃$︿★? 1 题面 一列火车n节车厢,依次编号为1,2,3,…,n。每节车厢有两种运动方式,进栈与出栈,问n节车厢出栈的可能排列方式有多少种。 输入…...
Unity学习日记12(导航走路相关、动作完成度返回参数)
目录 动作的曲线与函数 创建遮罩 导航走路 设置导航网格权重 动作的曲线与函数 执行动作,根据动作完成度返回参数。 函数,在代码内执行同名函数即可调用。在执行关键帧时调用。 创建遮罩 绿色为可效用位置 将其运用到Animator上的遮罩,可…...

基于bearpi的智能小车--Qt上位机设计
基于bearpi的智能小车--Qt上位机设计 前言一、界面原型1.主界面2.网络配置子窗口模块二、设计步骤1.界面原型设计2.控件添加信号槽3.源码解析3.1.网络链接核心代码3.2.网络设置子界面3.3.小车控制核心代码总结前言 最近入手了两块小熊派开发板,借智能小车案例,进行鸿蒙设备学…...
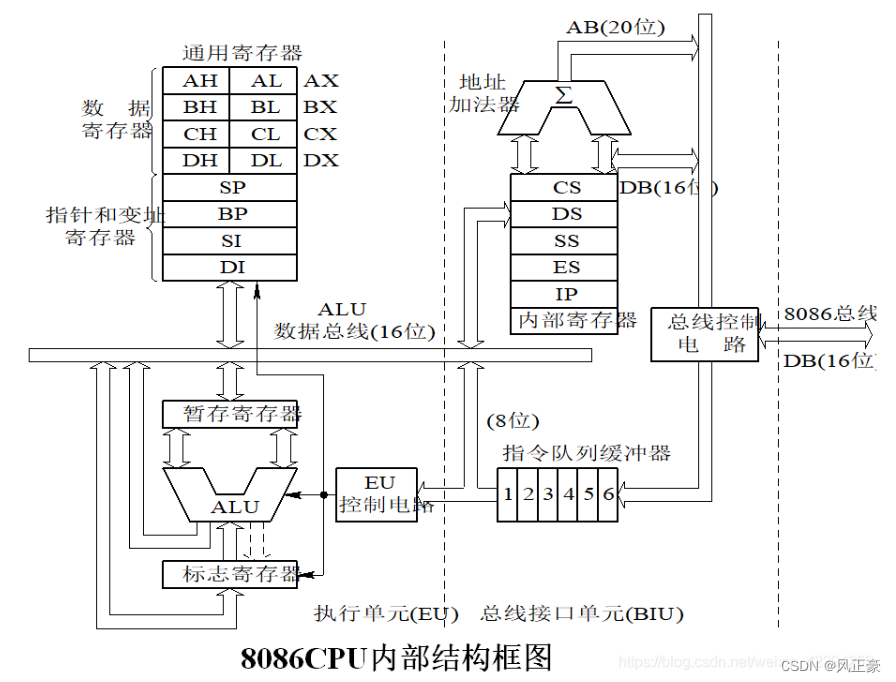
汇编语言与微机原理(1)基础知识
前言(1)本人使用的是王爽老师的汇编语言第四版和学校发的微机原理教材配合学习。(2)推荐视频教程通俗易懂的汇编语言(王爽老师的书);贺老师C站账号网址;(3)文…...

ASEMI代理瑞萨TW8825-LA1-CR汽车芯片
编辑-Z TW8825-LA1-CR在单个封装中集成了创建多用途车载LCD显示系统所需的许多功能。它集成了高质量的2D梳状NTSC/PAL/SECAM视频解码器、三重高速RGB ADC、高质量缩放器、多功能OSD和高性能MCU。TW8825-LA1-CR其图像视频处理能力包括任意缩放、全景缩放、图像镜像、图像调整和…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...
